专题9-6 双曲线测-2018年高考数学文一轮复习讲练测 含解析 精品

一、填空题1．若实数k 满足0＜k ＜9，则曲线x 225－y 29－k ＝1与曲线x 225－k －y 29＝1的________相等．【解析】由0<k <9，易知两曲线均为双曲线且焦点都在x 轴上，由25＋9－k ＝25－k ＋9，得两双曲线的焦距相等．2．已知双曲线C 的渐近线方程为y ＝±2x ，且经过点(2,2)，则C 的方程为________．【解析】由题意，设双曲线C 的方程为y 24－x 2＝λ(λ≠0)，因为双曲线C 过点(2,2)，则224－22＝λ，解得λ＝－3，所以双曲线C 的方程为y 24－x 2＝－3，即x 23－y 212＝1. 3．设F 1，F 2分别是双曲线x 2a 2－y 2b2＝1的左、右焦点，若双曲线上存在点A ，使∠F 1AF 2＝90°且|AF 1|＝3|AF 2|，则双曲线的离心率为________．【解析】因为∠F 1AF 2＝90°，故|AF 1|2＋|AF 2|2＝|F 1F 2|2＝4c 2，又|AF 1|＝3|AF 2|，且|AF 1|－|AF 2|＝2a ，所以|AF 1|＝3a ，|AF 2|＝a ，则10a 2＝4c 2，即c 2a 2＝52，故e ＝c a ＝102(负值舍去)．4．设双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点是F ，左、右顶点分别是A 1，A 2，过F 作A 1A 2的垂线与双曲线交于B, C 两点．若A 1B ⊥A 2C ，则该双曲线的渐近线的斜率为________．5． (2017·江南十校联考)已知l 是双曲线C ：x 22－y 24＝1的一条渐近线，P 是l 上的一点，F 1，F 2分别是C的左、右焦点，若1PF ·2PF ＝0，则点P 到x 轴的距离为________．【解析】由题意知F 1(－6，0)，F 2(6，0)，不妨设l 的方程为y ＝2x ，点P (x 0，2x 0)，由1PF ·2PF ＝(－6－x 0，－2x 0)·(6－x 0，－2x 0)＝3x 20－6＝0，得x 0＝±2，故点P 到x 轴的距离为2|x 0|＝2.6．已知双曲线x 2a 2－y 2b2＝1与直线y ＝2x 有交点，则双曲线离心率的取值范围为________．【解析】∵双曲线的一条渐近线方程为y ＝b a x ，则由题意得b a ＞2，∴e ＝c a＝ 1＋⎝ ⎛⎭⎪⎫b a2＞1＋4＝ 5.即双曲线离心率的取值范围为(5，＋∞)．7．已知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)与椭圆x 29＋y 24＝1有相同的焦点，且双曲线C 的渐近线方程为y ＝±2x ，则双曲线C 的方程为________________． 【答案】x 2－y 24＝1 【解析】易得椭圆的焦点为(－5，0)，(5，0)，∴⎩⎪⎨⎪⎧a 2＋b 2＝5，ba＝2，∴a 2＝1，b 2＝4，∴双曲线C 的方程为x 2－y 24＝1.8．过双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左焦点F 1作斜率为1的直线，该直线与双曲线的两条渐近线的交点分别为A ，B ，若v 1F A ＝AB ，则双曲线的渐近线方程为____________． 【答案】3x ±y ＝09．设F 1，F 2分别是双曲线x 2－y 2b2＝1的左、右焦点，A 是双曲线上在第一象限内的点，若|AF 2|＝2且∠F 1AF 2＝45°，延长AF 2交双曲线右支于点B ，则△F 1AB 的面积等于______． 【答案】4【解析】由题意可得|AF 2|＝2，|AF 1|＝4，则|AB |＝|AF 2|＋|BF 2|＝2＋|BF 2|＝|BF 1|.又∠F 1AF 2＝45°，所以△ABF 1是以AF 1为斜边的等腰直角三角形，则|AB |＝|BF 1|＝22，所以其面积为12×22×22＝4.10．已知双曲线E ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)，若矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是________．【答案】2二、解答题11．已知双曲线的中心在原点，焦点F 1，F 2在坐标轴上，离心率为2，且过点(4， －10)．点M (3，m )在双曲线上． (1)求双曲线的方程； (2)求证：1MF ·2MF ＝0； (3)求△F 1MF 2的面积． 解：(1)∵e ＝2，∴双曲线的实轴、虚轴相等． 则可设双曲线方程为x 2－y 2＝λ. ∵双曲线过点(4，－10)， ∴16－10＝λ，即λ＝6. ∴双曲线方程为x 26－y 26＝1.(2)证明：不妨设F 1，F 2分别为左、右焦点， 则1MF ＝(－23－3，－m )，2MF ＝(23－3，－m )．∴1MF ·2MF ＝(3＋23)×(3－23)＋m 2＝－3＋m 2，∵M 点在双曲线上，∴9－m 2＝6，即m 2－3＝0， ∴1MF ·2MF ＝0. (3)△F 1MF 2的底|F 1F 2|＝4 3. 由(2)知m ＝± 3.∴△F 1MF 2的高h ＝|m |＝3， ∴S △F 1MF 2＝12×43×3＝6.12．中心在原点，焦点在x 轴上的椭圆与双曲线有共同的焦点F 1，F 2，且|F 1F 2|＝213，椭圆的长半轴长与双曲线实半轴长之差为4，离心率之比为3∶7. (1)求椭圆和双曲线的方程；(2)若P 为这两曲线的一个交点，求cos ∠F 1PF 2的值．。

1．双曲线定义平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于|F1F 2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P＝{M｜｜｜MF1|－｜MF2｜｜＝2a｝,｜F1F2|＝2c，其中a，c 为常数且a〉0，c〉0.（1）当2a〈|F1F2|时，P点的轨迹是双曲线；(2)当2a＝｜F1F2｜时，P点的轨迹是两条射线；（3)当2a〉｜F1F2|时，P点不存在．2．双曲线的标准方程和几何性质标准方程错误!－错误!＝1(a>0,b〉0)错误!－错误!＝1（a〉0,b>0)图形【知识拓展】巧设双曲线方程（1)与双曲线错误!－错误!＝1（a〉0,b>0）有共同渐近线的方程可表示为x2a2－错误!＝t(t≠0）．（2)过已知两个点的双曲线方程可设为错误!＋错误!＝1（mn〈0）．【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×")(1)平面内到点F1(0，4），F2（0,－4）距离之差的绝对值等于8的点的轨迹是双曲线．( ×)(2）方程错误!－错误!＝1（mn〉0）表示焦点在x轴上的双曲线．( ×）（3）双曲线方程x2m2－错误!＝λ(m>0，n〉0，λ≠0)的渐近线方程是错误!－错误!＝0，即错误!±错误!＝0。

( √)(4)等轴双曲线的渐近线互相垂直，离心率等于错误!.（√）(5）若双曲线错误!－错误!＝1（a〉0，b〉0）与错误!－错误!＝1（a>0，b〉0)的离心率分别是e1,e2，则错误!＋错误!＝1（此结论中两条双曲线称为共轭双曲线)．（√）1．(教材改编）若双曲线错误!－错误!＝1 (a〉0,b〉0）的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( ）A。

5 B．5C.错误!D．2答案A解析由题意得b＝2a，又a2＋b2＝c2,∴5a2＝c2。

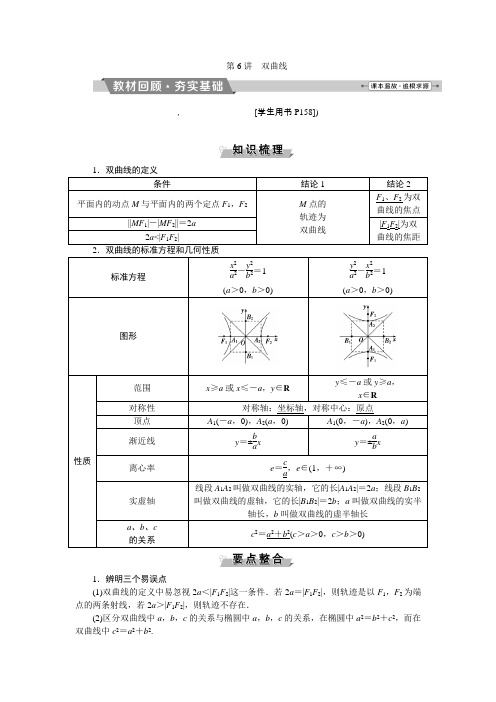
第6讲双曲线,[学生用书P158])1．辨明三个易误点(1)双曲线的定义中易忽视2a＜|F1F2|这一条件．若2a＝|F1F2|，则轨迹是以F1，F2为端点的两条射线，若2a＞|F1F2|，则轨迹不存在．(2)区分双曲线中a，b，c的关系与椭圆中a，b，c的关系，在椭圆中a2＝b2＋c2，而在双曲线中c2＝a2＋b2.(3)双曲线的离心率e ∈(1，＋∞)，而椭圆的离心率e ∈(0，1)． 2．求双曲线标准方程的两种方法 (1)定义法根据题目的条件，判断是否满足双曲线的定义，若满足，求出相应的a ，b ，c ，即可求得方程．(2)待定系数法①与双曲线x 2a 2－y 2b 2＝1共渐近线的可设为x 2a 2－y 2b 2＝λ(λ≠0)；②若渐近线方程为y ＝±b a x ，则可设为x 2a 2－y 2b 2＝λ(λ≠0)；③若过两个已知点，则可设为x 2m ＋y 2n＝1(mn ＜0)．3．双曲线几何性质的三个关注点(1)“六点”：两焦点、两顶点、两虚轴端点； (2)“四线”：两对称轴(实、虚轴)、两渐近线；(3)“两形”：中心、顶点、虚轴端点构成的三角形；双曲线上的一点(不包括顶点)与两焦点构成的三角形．1.教材习题改编 双曲线y 264－x 216＝1上一点P 到一个焦点的距离为4，则P 到另一个焦点的距离为( )A ．20B ．16C ．12D ．8A [解析] 设P 到另一个焦点的距离为d ， 则|d －4|＝2×8＝16， 所以d ＝20，故选A.2.教材习题改编 双曲线C 的焦点为(－6，0)，(6，0)，且经过点(－5，2)，则双曲线的标准方程为( )A ．x 220－y 24＝1B ．x 220－y 216＝1C ．y 220－x 216＝1D ．y 220－x 24＝1B [解析] 2a ＝|（－5＋6）2＋22－|（－5－6）2＋22＝4 5.所以a ＝25，又c ＝6， 所以b 2＝c 2－a 2＝36－20＝16.所以双曲线的标准方程为x 220－y 216＝1.故选B.3．(2017·南昌模拟)若双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线的倾斜角为π6，则双曲线C 的离心率为( )A ．2或 3B ．233C ．2或233D ．2B [解析] 由题意知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的渐近线方程为y ＝±b a x ，所以ba ＝tan π6＝33，所以a ＝3b ，c ＝a 2＋b 2＝2b ，故双曲线C 的离心率e ＝c a ＝2b 3b＝233.4.教材习题改编 与椭圆x 249＋y 224＝1有相同焦点且离心率为54的双曲线的标准方程为________．[解析] 椭圆x 249＋y 224＝1的焦点为(±5，0)．设双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)，则c ＝5，c a ＝54，所以a ＝4，b 2＝c 2－a 2＝25－16＝9，所以所求双曲线的标准方程为x 216－y 29＝1.[答案] x 216－y 29＝15.教材习题改编 经过点A (3，－1)，且对称轴都在坐标轴上的等轴双曲线方程为________．[解析] 设双曲线的方程为x 2a 2－y 2a 2＝±1(a >0)，把点A (3，－1)代入，得a 2＝8，故所求方程为x 28－y 28＝1.[答案] x 28－y 28＝1双曲线的定义[学生用书P159][典例引领](1)设双曲线x 2－y 28＝1的两个焦点为F 1，F 2，P 是双曲线上的一点，且|PF 1|∶|PF 2|＝3∶4，则△PF 1F 2的面积等于( )A ．103B ．8 3C ．8 5D ．16 5(2)(2017·云南省第一次统一检测)已知F 1、F 2是双曲线M ：y 24－x 2m 2＝1的焦点，y ＝255x是双曲线M 的一条渐近线，离心率等于34的椭圆E 与双曲线M 的焦点相同，P 是椭圆E 与双曲线M 的一个公共点，则|PF 1|·|PF 2|＝________．【解析】 (1)依题意|F 1F 2|＝6，|PF 2|－|PF 1|＝2， 因为|PF 1|∶|PF 2|＝3∶4， 所以|PF 1|＝6，|PF 2|＝8， 所以等腰三角形PF 1F 2的面积 S ＝12×8× 62－⎝⎛⎭⎫822＝8 5.(2)由题意易得，双曲线的方程为y 24－x 25＝1，椭圆的方程为x 27＋y 216＝1，不妨设|PF 1|>|PF 2|，从而可知⎩⎪⎨⎪⎧|PF 1|＋|PF 2|＝8，|PF 1|－|PF 2|＝4⇒⎩⎪⎨⎪⎧|PF 1|＝6，|PF 2|＝2⇒|PF 1|·|PF 2|＝12.【答案】 (1)C (2)12若本例(1)中“|PF 1|∶|PF 2|＝3∶4”改为“PF 1⊥PF 2”，其他条件不变，如何求解．[解] 设|PF 1|＝m ，|PF 2|＝n ，则⎩⎪⎨⎪⎧m 2＋n 2＝36，m 2＋n 2－2mn ＝4，解得mn ＝16，所以S △PF 1F 2＝12mn ＝8.(1)在应用双曲线定义时，要注意定义中的条件，搞清所求轨迹是双曲线，还是双曲线的一支．若是双曲线的一支，则需确定是哪一支．(2)在“焦点三角形”中，正弦定理、余弦定理、双曲线的定义是经常使用的知识点．另外，还经常结合||PF 1|－|PF 2||＝2a ，运用平方的方法，建立它与|PF 1||PF 2|的联系．[通关练习]1．已知F 1，F 2为双曲线C ：x 2－y 2＝1的左、右焦点，点P 在C 上，∠F 1PF 2＝60°，则|PF 1|·|PF 2|等于( )A ．2B ．4C ．6D ．8B [解析] 由双曲线的方程得a ＝1，c ＝2， 由双曲线的定义得||PF 1|－|PF 2||＝2. 在△PF 1F 2中，由余弦定理得|F 1F 2|2＝|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|cos 60°， 即(22)2＝|PF 1|2＋|PF 2|2－|PF 1|·|PF 2| ＝(|PF 1|－|PF 2|)2＋|PF 1|·|PF 2| ＝22＋|PF 1|·|PF 2|. 解得|PF 1|·|PF 2|＝4.故选B.2．已知圆C ：(x －3)2＋y 2＝4，定点A (－3，0)，则过定点A 且和圆C 外切的动圆圆心M 的轨迹方程为________．[解析] 设动圆M 的半径为R ， 则|MC |＝2＋R ，|MA |＝R ， 所以|MC |－|MA |＝2，由双曲线的定义知，M 点的轨迹是以A ，C 为焦点的双曲线的左支，且a ＝1，c ＝3， 所以b 2＝8，则动圆圆心M 的轨迹方程为x 2－y 28＝1(x ≤－1)．[答案] x 2－y 28＝1(x ≤－1)双曲线的标准方程[学生用书P160][典例引领](1)(2016·高考天津卷)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为( )A ．x 24－y 2＝1B ．x 2－y 24＝1C ．3x 220－3y 25＝1D ．3x 25－3y 220＝1(2)设双曲线与椭圆x 227＋y 236＝1有共同的焦点，且与椭圆相交，其中一个交点的坐标为(15，4)，则此双曲线的标准方程是________．【解析】 (1)由题意得c ＝5，b a ＝12，则a ＝2，b ＝1，所以双曲线的方程为x 24－y 2＝1.(2)法一：椭圆x 227＋y 236＝1的焦点坐标是(0，±3)，设双曲线方程为y 2a 2－x 2b 2＝1(a >0，b >0)，根据双曲线的定义知2a ＝|（15－0）2＋（4－3）2－（15－0）2＋（4＋3）2|＝4，故a ＝2.又b 2＝32－22＝5，故所求双曲线的标准方程为y 24－x 25＝1.法二：椭圆x 227＋y 236＝1的焦点坐标是(0，±3)．设双曲线方程为y 2a 2－x 2b 2＝1(a >0，b >0)，则a 2＋b 2＝9①，又点(15，4)在双曲线上，所以16a 2－15b 2＝1②，联立①②解得a 2＝4，b 2＝5.故所求双曲线的标准方程为y 24－x 25＝1.法三：设双曲线的方程为x 227－λ＋y 236－λ＝1(27<λ<36)，由于双曲线过点(15，4)，故1527－λ＋1636－λ＝1， 解得λ1＝32，λ2＝0，经检验λ1＝32，λ2＝0都是分式方程的根，但λ＝0不符合题意，应舍去，所以λ＝32. 故所求双曲线的标准方程为y 24－x 25＝1.【答案】 (1)A (2)y 24－x 25＝1求双曲线标准方程的一般方法(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a 、b 、c 的方程并求出a 、b 、c 的值与双曲线x 2a 2－y 2b2＝±1，(a >0，b >0)有相同渐近线时可设所求双曲线方程为x 2a 2－y 2b2＝λ(λ≠0，a >0，b >0)．(2)定义法：依定义得出距离之差的等量关系式，求出a 的值，由定点位置确定c 的值．分别求出适合下列条件的双曲线的标准方程：(1)虚轴长为12，离心率为54；(2)焦距为26，且经过点M (0，12)． [解] (1)设双曲线的标准方程为 x 2a 2－y 2b 2＝1或y 2a 2－x 2b2＝1(a >0，b >0)． 由题意知，2b ＝12，e ＝c a ＝54，所以b ＝6，c ＝10，a ＝8.所以双曲线的标准方程为x 264－y 236＝1或y 264－x 236＝1.(2)因为双曲线经过点M (0，12)， 所以M (0，12)为双曲线的一个顶点， 故焦点在y 轴上，且a ＝12.又2c ＝26，所以c ＝13.所以b 2＝c 2－a 2＝25. 所以双曲线的标准方程为y 2144－x 225＝1.双曲线的几何性质(高频考点)[学生用书P161]双曲线的几何性质及应用，是高考命题的热点，多以选择题或填空题的形式呈现，多为容易题或中档题．高考对双曲线的几何性质的考查主要有以下三个命题角度： (1)求双曲线的离心率(或范围)； (2)求双曲线的渐近线方程； (3)由双曲线的性质求方程．[典例引领](1)(2016·高考山东卷)已知双曲线E ：x 2a 2－y 2b2＝1(a >0，b >0)．矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是__________．(2)过双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点F 作圆O ：x 2＋y 2＝a 2的两条切线，切点为A ，B ，双曲线左顶点为C ，若∠ACB ＝120°，则双曲线的渐近线方程为________．【解析】 (1)如图，不妨设|AB |＝3，则|BC |＝2，双曲线的左、右焦点分别为F 1，F 2，则AB 的中点为F 1，故|DF 1|＝52，|DF 2|＝32，根据双曲线的定义知2a ＝1，又2c ＝2，所以该双曲线的离心率为2c2a＝2.(2)如图所示，连接OA ，OB ，设双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的焦距为2c (c >0)，则C (－a ，0)，F (－c ，0)．由双曲线和圆的对称性知，点A 与点B 关于x 轴对称，则∠ACO ＝∠BCO ＝12∠ACB ＝12×120°＝60°.因为|OA |＝|OC |＝a ，所以△ACO 为等边三角形，所以∠AOC ＝60°. 因为F A 与圆O 切于点A ，所以OA ⊥F A ，在Rt △AOF 中，∠AFO ＝90°－∠AOF ＝90°－60°＝30°，所以|OF |＝2|OA |，即c ＝2a ， 所以b ＝c 2－a 2＝（2a ）2－a 2＝3a ，故双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的渐近线方程为y ＝±bax ，即y ＝±3x .【答案】 (1)2 (2)y ＝±3x与双曲线几何性质有关问题的解题策略(1)求双曲线的离心率(或范围)．依据题设条件，将问题转化为关于a ，c 的等式(或不等式)，解方程(或不等式)即可求得．(2)求双曲线的渐近线方程．依据题设条件，求双曲线中a ，b 的值或a 与b 的比值，进而得出双曲线的渐近线方程．(3)求双曲线方程．依据题设条件，求出a ，b 的值或依据双曲线的定义，即可求双曲线的方程．(4)求双曲线焦点(焦距)、实虚轴的长．依题设条件及a ，b ，c 之间的关系求解． [题点通关]角度一 求双曲线的离心率(或范围) 1．(2015·高考全国卷Ⅱ)已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，△ABM 为等腰三角形，且顶角为120°，则E 的离心率为( )A ．5B ．2C ． 3D ． 2D [解析] 不妨取点M 在第一象限，如图所示，设双曲线方程为x 2a 2－y 2b 2＝1(a ＞0，b＞0)，则|BM |＝|AB |＝2a ，∠MBx ＝180°－120°＝60°，所以M 点的坐标为(2a ，3a )． 因为M 点在双曲线上， 所以4a 2a 2－3a 2b 2＝1，a ＝b ，所以c ＝2a ，e ＝ca ＝ 2.故选D.角度二 求双曲线的渐近线方程2．若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为3，则其渐近线方程为( )A ．y ＝±2xB ．y ＝±2xC ．y ＝±12xD ．y ＝±22xA [解析] 由于双曲线x 2a 2－y 2b 2＝1的离心率为3，故e 2＝c 2a 2＝a 2＋b 2a 2＝1＋b 2a2＝3，所以ba＝2，故其渐近线方程为y ＝±2x ，选A.角度三 由双曲线的性质求方程3．已知双曲线的渐近线方程为y ＝±12x ，且经过点A (2，－3)，则双曲线的标准方程为( )A ．x 28－y 232＝1B ．y 28－x 232＝1C ．x 274－y 27＝1D ．x 27－y 274＝1B [解析] 若焦点在x 轴上，设所求双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)，因为双曲线的渐近线方程为y ＝±12x ，所以b a ＝12.①因为A (2，－3)在双曲线上，所以4a 2－9b 2＝1.②①②联立，无解．若焦点在y 轴上，设所求双曲线的标准方程为y 2a 2－x 2b 2＝1(a >0，b >0)，因为双曲线的渐近线方程为y ＝±12x ，所以a b ＝12.③因为A (2，－3)在双曲线上，所以9a 2－4b 2＝1.④③④联立，解得a 2＝8，b 2＝32. 所以所求双曲线的标准方程为y 28－x 232＝1., [学生用书P161])——方程思想在求离心率中的应用(2017·沈阳四校联考)设双曲线x 2a 2－y 2b2＝1(0<a <b )的半焦距为c ，直线l 过(a ，0)、(0，b )两点．已知原点到直线l 的距离为34c ，则双曲线的离心率为________． 【解析】 由已知，得直线l 的方程为ay ＋bx －ab ＝0，因为原点到直线l 的距离为34c ， 所以aba 2＋b 2＝34c ，又c 2＝a 2＋b 2， 所以4ab ＝3c 2，两边平方，得16a 2b 2＝3c 4， 即16a 2(c 2－a 2)＝3c 4，两边同除以a 4，并整理，得 3e 4－16e 2＋16＝0，所以e 2＝4或e 2＝43.由0<a <b ，得e 2＝a 2＋b 2a 2＝1＋b 2a2>2，所以e 2＝4.故e ＝2. 【答案】 2(1)本题利用方程思想，将已知条件转化为关于a ，c 的方程，然后求出离心率e .(2)求解椭圆、双曲线的离心率或离心率的取值范围的方法通常是根据条件列出关于a ，c 的齐次方程或不等式，然后再转化成关于e 的方程或不等式求解．已知点F 是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左焦点，点E 是该双曲线的右顶点，过F 且垂直于x 轴的直线与双曲线交于A ，B 两点，若△ABE 是锐角三角形，则该双曲线的离心率e 的取值范围是( )A ．(1，＋∞)B ．(1，2)C ．(2，1＋2)D ．(1，1＋2)B [解析] 若△ABE 是锐角三角形，只需∠AEF <45°，在Rt △AFE 中，|AF |＝b 2a ，|FE |＝a ＋c ，则b 2a <a ＋c ⇒b 2<a 2＋ac ⇒2a 2－c 2＋ac >0⇒e 2－e －2<0⇒－1<e <2，又e >1，则1<e <2，故选B., [学生用书P343(独立成册)])1．(2017·石家庄一模)已知双曲线的离心率为2，焦点是(－4，0)，(4，0)，则双曲线的方程为( )A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 210－y 26＝1D ．x 26－y 210＝1A [解析] 已知双曲线的离心率为2，焦点是(－4，0)，(4，0)，则c ＝4，a ＝2，b 2＝12，双曲线方程为x 24－y 212＝1，故选A.2．(2017·惠州调研)若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为3，则其渐近线的斜率为( )A ．±2B ．± 2C ．±12D ．±22B [解析] 因为双曲线x 2a 2－y 2b 2＝1的离心率为3，所以e ＝ca＝1＋b 2a 2＝3，解得ba＝2， 所以其渐近线的斜率为±2.故选B.3．设F 1，F 2分别是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，若双曲线上存在点A ，使∠F 1AF 2＝90°且|AF 1|＝3|AF 2|，则双曲线的离心率为( )A ．52B ．102C ．152D ． 5B [解析] 因为∠F 1AF 2＝90°， 故|AF 1|2＋|AF 2|2＝|F 1F 2|2＝4c 2， 又|AF 1|＝3|AF 2|，且|AF 1|－|AF 2|＝2a ， 故10a 2＝4c 2，故c 2a 2＝52，故e ＝c a ＝102.4．设F 1，F 2是双曲线x 2－y 224＝1的两个焦点，P 是双曲线上的一点，且3|PF 1|＝4|PF 2|，则△PF 1F 2的面积等于( )A ．4 2B ．8 3C ．24D ．48C [解析] 由题知，⎩⎪⎨⎪⎧|PF 1|－|PF 2|＝23|PF 1|＝4|PF 2|，解得⎩⎪⎨⎪⎧|PF 1|＝8|PF 2|＝6.又由|F 1F 2|＝10可得△PF 1F 2是直角三角形， 则S △PF 1F 2＝12|PF 1|×|PF 2|＝24.5．(2017·江南十校联考(一))已知l 是双曲线C ：x 22－y 24＝1的一条渐近线，P 是l 上的一点，F 1，F 2分别是C 的左、右焦点，若PF 1→·PF 2→＝0，则点P 到x 轴的距离为( )A ．233B ． 2C ．2D ．263C [解析] 由题意知F 1(－6，0)，F 2(6，0)，不妨设l 的方程为y ＝2x ，点P (x 0，2x 0)，由 PF 1→·PF 2→＝(－6－x 0，－2x 0)·(6－x 0，－2x 0)＝3x 20－6＝0，得x 0＝±2，故点P 到x 轴的距离为2|x 0|＝2，故选C.6．已知焦点在y 轴上的双曲线C 的中心是原点O ，离心率等于52，以双曲线C 的一个焦点为圆心，1为半径的圆与双曲线C 的渐近线相切，则双曲线C 的方程为( )A ．y 216－x 24＝1B ．y 2－x 24＝1C ．y 24－x 2＝1D ．x 24－y 2＝1C [解析] 设双曲线方程为y 2a 2－x 2b 2＝1(a >0，b >0)，所以其渐近线方程为y ＝±ab x ，其中一个焦点为F 1(0，－c )，则以F 1为圆心，1为半径的圆的方程为x 2＋(y ＋c )2＝1.因为点F 1到直线y ＝abx 的距离等于该圆的半径，所以|－bc |a 2＋b 2＝1，所以b 2c 2＝a 2＋b 2，又因为c 2＝a 2＋b 2，所以b 2＝1，因为e ＝c a ＝52，所以c 2＝54a 2，解得a 2＝4，所以双曲线的方程为y 24－x2＝1.故选C.7．若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线经过点(3，－4)，则此双曲线的离心率为________．[解析] 由双曲线的渐近线过点(3，－4)知b a ＝43，所以b 2a 2＝169.又b 2＝c 2－a 2，所以c 2－a 2a 2＝169，即e 2－1＝169，所以e 2＝259，所以e ＝53.[答案] 538．已知双曲线x 2m －y 23m ＝1的一个焦点是(0，2)，椭圆y 2n －x 2m ＝1的焦距等于4，则n ＝________．[解析] 因为双曲线的焦点(0，2)，所以焦点在y 轴上，所以双曲线的方程为y 2－3m －x 2－m ＝1，即a 2＝－3m ，b 2＝－m ，所以c 2＝－3m －m ＝－4m ＝4，解得m ＝－1.所以椭圆方程为y 2n＋x 2＝1，且n >0且n ≠1，又椭圆的焦距为4，所以c 2＝n －1＝4或1－n ＝4，解得n ＝5或－3(舍去)．[答案] 59．(2016·高考北京卷)双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝________．[解析] 双曲线x 2a 2－y 2b 2＝1的渐近线方程为y ＝±ba x ，由已知可得两条渐近线方程互相垂直，由双曲线的对称性可得ba ＝1.又正方形OABC 的边长为2，所以c ＝22，所以a 2＋b 2＝c 2＝(22)2，解得a ＝2.[答案] 210．设双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的半焦距为c .已知原点到直线l ：bx ＋ay ＝ab 的距离等于14c ＋1，则c 的最小值为________．[解析] 根据已知，得aba 2＋b 2＝14c ＋1， 又ab ≤a 2＋b 22＝c 22，故14c ＋1≤c2，解得c ≥4，即c 的最小值为4. [答案] 411．已知双曲线的中心在原点，焦点F 1，F 2在坐标轴上，离心率为2，且过点(4，－10)，点M (3，m )在双曲线上．(1)求双曲线的方程；(2)求证：MF 1→·MF 2→＝0； (3)求△F 1MF 2的面积．[解] (1)因为e ＝2，则双曲线的实轴、虚轴相等． 所以可设双曲线方程为x 2－y 2＝λ. 因为双曲线过点(4，－10)， 所以16－10＝λ，即λ＝6. 所以双曲线方程为x 2－y 2＝6.(2)证明：设F 1(－23，0)，F 2(23，0)， 则MF 1→＝(－23－3，－m )， MF 2→＝(23－3，－m )．所以MF 1→·MF 2→＝(3＋23)×(3－23)＋m 2 ＝－3＋m 2，因为M 点在双曲线上， 所以9－m 2＝6，即m 2－3＝0， 所以MF 1→·MF 2→＝0.(3)△F 1MF 2的底边长|F 1F 2|＝4 3. 由(2)知m ＝±3.所以△F 1MF 2的高h ＝|m |＝3， 所以S △F 1MF 2＝12×43×3＝6.12．过双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点F 1作斜率为1的直线，该直线与双曲线的两条渐近线的交点分别为A ，B ，若F 1A →＝AB →，则双曲线的渐近线方程为________．[解析] 设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y 1＝x 1＋c ，y 1＝－ba x 1得x 1＝－ac a ＋b ，y 1＝bca ＋b ， 由⎩⎪⎨⎪⎧y 2＝x 2＋c ，y 2＝ba x 2，得x 2＝ac b －a ，y 2＝bcb －a ， 由已知得－2ac a ＋b ＝－c ＋acb －a ，所以b ＝3a .所以双曲线的渐近线方程为3x ±y ＝0. [答案] 3x ±y ＝013．中心在原点，焦点在x 轴上的椭圆与双曲线有共同的焦点F 1，F 2，且|F 1F 2|＝213，椭圆的长半轴长与双曲线实半轴长之差为4，离心率之比为3∶7.(1)求椭圆和双曲线的方程；(2)若P 为这两曲线的一个交点，求cos ∠F 1PF 2的值．[解] (1)由题知c ＝13，设椭圆方程为x 2a 2＋y 2b 2＝1，双曲线方程为x 2m 2－y 2n2＝1，则⎩⎪⎨⎪⎧a －m ＝4，7·13a ＝3·13m ，解得a ＝7，m ＝3. 所以b ＝6，n ＝2.所以椭圆方程为x 249＋y 236＝1，双曲线方程为x 29－y 24＝1.(2)不妨设F 1，F 2分别为左、右焦点，P 是第一象限的一个交点，则|PF 1|＋|PF 2|＝14，|PF 1|－|PF 2|＝6，所以|PF 1|＝10，|PF 2|＝4. 又|F 1F 2|＝213，所以cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1||PF 2|＝102＋42－（213）22×10×4＝45.14．(2017·湛江模拟)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的右焦点为F (c ，0)．(1)若双曲线的一条渐近线方程为y ＝x 且c ＝2，求双曲线的方程；(2)以原点O 为圆心，c 为半径作圆，该圆与双曲线在第一象限的交点为A ，过A 作圆的切线，斜率为－3，求双曲线的离心率．[解] (1)因为双曲线的渐近线方程为y ＝±ba x ，所以a ＝b ，所以c 2＝a 2＋b 2＝2a 2＝4， 所以a 2＝b 2＝2，所以双曲线方程为x 22－y 22＝1.(2)设点A 的坐标为(x 0，y 0)，所以直线AO 的斜率满足y 0x 0·(－3)＝－1，所以x 0＝3y 0，①依题意，圆的方程为x 2＋y 2＝c 2，将①代入圆的方程得3y 20＋y 20＝c 2，即y 0＝12c ， 所以x 0＝32c ，所以点A 的坐标为⎝⎛⎭⎫32c ，12c ， 代入双曲线方程得34c 2a 2－14c 2b 2＝1，即34b 2c 2－14a 2c 2＝a 2b 2，② 又因为a 2＋b 2＝c 2，所以将b 2＝c 2－a 2代入②式，整理得 34c 4－2a 2c 2＋a 4＝0， 所以3⎝⎛⎭⎫c a 4－8⎝⎛⎭⎫c a 2＋4＝0， 所以(3e 2－2)(e 2－2)＝0， 因为e ＞1，所以e ＝2，所以双曲线的离心率为 2.。

双曲线部分1、双曲线方程为x 2—2y 2=1，则它的右焦点坐标为（C ）库B 、"逅,0C 、込〕l 丿 l 2丿l 2丿D 、 3,02、如果双曲线的两个焦点分别为 F i （-3,0）、F 2（3,0），—条渐近线方程为 y —..2x ， 那么它的两条准线间的距离是（ A 、6 3C 、2D 、 13、已知双曲线 2xa 2 b2y2 =1 a 0,b 0的一条渐近线方程是y —.3x ，它的一个焦点在抛物线 -24x 的准线上，则双曲线的方程为（B ）=136 1082 2B 、—9 27 2 2C 、丄丄=1108 36 2 2D 、三-上=127 924、设双曲线务 a 2% =1（a 0,b0）的离心率为 3，且它的一条准线与抛物线b 2-4x 的准线重合，则此双曲线的方程为（D ）A 、 2 2x y 1 12 242 2r x y B 、148 962 2c 、—1332 2r x yD 、5、设双曲线 2x ~2a2”（a 0,b 0）的虚轴长为2,焦距为2・3，则双曲线的渐近线方程为（ A 、 y = 2xB 、y = 2xC y~x2D 、A 、A 、3x 二4y =0B 、3x 二 5y = 0 CC 4x 二3y = 0D 、5x 二4y = 03A 、 6B 、3D 、一个公共点，则双曲线的离心率为围是（B ）为-1的直线，该直线与双曲线的两条渐近线的交点分别为B,C 。

若AB 丿BC ，2则双曲线的离心率是（C ） A 、. 2B 、、3C 、. 5D 、102 211、（双曲线离心率问题）设双曲线与* =1（a 0,b 0）的左、右焦点分别是a bF 1,F 2，过点F 2的直线交双曲线右支于不同的两点 M,N ，若 MNF 1为正三角形,则该双曲线的离心率为（B ）7、（双曲线离心率问题）设双曲线a 2b 21的一条渐近线与抛物线y = x 2 • 1只有A 、B 、5C 、,5D 、 (5)8、（双曲线离心率问题）设a 1，则双曲线x 22y二1的离心率e 的取值范 （a 1）2A 、（ .2,2）B 、（ .2,5）C 、 （2,5）D 、（2, 5）x 29、（双曲线离心率问题）已知双曲线 C ：r ab 21 a 0,b 0的右焦点为F ，过F 且斜率为3的直线交C 于A, B 两点，若=4FB ，则C 的离心率为（A ）A 、 105 -00G7 - 5BB（双曲线离心率冋题）过双曲线 D 、2 2务-每=1（a0,b 0）的右顶点A 作斜率a b12、（双曲线离心率问题）设双曲线的一个焦点为 F ，虚轴的一个端点为B ，如果 直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（ D ）A 、 2B 、 3C 、2D 、3解析：由双曲线的第二定义知e =亘上=2 • 1c e2 214、（双曲线离心率问题）过双曲线 —=1（a 0,b ■ 0）的右顶点A 作斜率为-1a b的直线，该直线与双曲线的两条渐近线的交点分别为 B,C ，若=-BT ，则双曲2线的离心率是（C ） A 、 、2B 、 、3C 、D 、■ 10解析：对于A a,0，则直线方程为x • y -a =0，直线与两渐近线的交点为B ，C,13、（双曲线离心率问题）若2RE 为双曲线X a2b 2 J 的左右焦点,O 为坐标原点,点P 在双曲线的左支上，点 M 在双曲线的右准线上，且满足: — —— OF i OM Fl "Mgg 廊）心），OF1则该双曲线的离心率为（a 2ab〜a 2 ab 、 巾［若二 / 2a 2b 2a 2b ，C （a^，一訐），则有心（口，一口ab ab），心，b ，a b ，22215、已知双曲线才斧1(b 5的左、右焦点分别是钉2，其一条渐近线方程 为y = x ，点P(, 3, y o )在双曲线上，则PF 1 • PF 2 =( C )A 、 -1B 、 12X17、已知双曲线—2与椭圆至多有一个交点的充要条件是(A )2 22解析：方程是1+^=1联立y=kx+2 可由也＜0可解得A 。

2018年高考数学讲练测【新课标版】【讲】第九章解析几何第六节双曲线【考纲解读】【知识清单】1.双曲线的定义及标准方程1．双曲线的定义满足以下三个条件的点的轨迹是双曲线(1)在平面内；(2)动点到两定点的距离的差的绝对值为一定值；(3)这一定值一定要小于两定点的距离．2．双曲线的标准方程对点练习：△【2017天津，文5】的左焦点为F，点A在双曲线的渐近线上，OAF 是边长为2的等边三角形（O为原点），则双曲线的方程为（）（A B C D【答案】D2. 双曲线的几何性质 双曲线的几何性质【2017课标II ，文5】若1a >，则双曲线 ）D. (1,2)【答案】Ca>，所以 C.，因为1【考点深度剖析】纵观近几年的高考试题，高考对双曲线的考查，主要考查以下几个方面：一是考查双曲线的标准方程，结合双曲线的定义及双曲线基本量之间的关系，利用待定系数法求解；二是考查双曲线的几何性质，较多地考查离心率、渐近线问题；三是考查双曲线与圆、椭圆或抛物线相结合的问题，综合性较强.命题以小题为主，多为选择题或填空题，近几年无解答题.【重点难点突破】考点1 双曲线的定义及标准方程【1-1】【2017课标3，理5】已知双曲线C＞0,b＞0)且C的方程为（）A B C D【答案】B【1-2】【2018届陕西省榆林市第二中学高三上学期期中】已知双曲线的两个焦点分别为，，点是双曲线上一点，且，则该双曲线的渐近线方程为（）A. B. C. D.【答案】C【解析】由双曲线定义知，所以.两个焦点分别为，，所以.所以有：,所以.双曲线的渐近线方程为.故选C.【综合点评】1.双曲线的轨迹类型是；2．双曲线标准方程的求解方法是”待定系数法”，“先定型，后计算”． 【领悟技法】1.待定系数法求双曲线方程的常用方法(1)与双曲线x 2a 2－y 2b 2＝1共渐近线的可设为x 2a 2－y 2b 2＝λ(λ≠0)；(2)若渐近线方程为y ＝±b a x ，则可设为x 2a 2－y 2b 2＝λ(λ≠0)；(3)若过两个已知点则设为x 2m ＋y 2n＝1(mn <0)．2．应用双曲线的定义需注意的问题：在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件，即“到两定点(焦点)的距离之差的绝对值为一常数，且该常数必须小于两定点的距离”．若定义中的“绝对值”去掉，点的轨迹是双曲线的一支．同时注意定义的转化应用．3．求双曲线方程时一是标准形式判断；二是注意a 、b 、c 的关系易错易混． 【触类旁通】【变式一】【2018届重庆市巴蜀中学高三9月月考】已知双曲线的左、右焦点分别为，点为异于的两点，且的中点在双曲线的左支上，点关于和的对称点分别为，则的值为（ ）A. 26B.C. 52D.【答案】D【解析】设MN 与双曲线的交点为点P ，由几何关系结合三角形中位线可得：，则：，点P 位于双曲线的左支，则：.本题选择D 选项.【变式二】已知双曲线的左、右焦点分别为，为的右支上一点，且，则的面积等于___________．【答案】48 【解析】由题意得，所以，根据双曲线的定义得，是等腰三角形，边上的高为，所以的面积等于．【综合点评】1、在焦点三角形中，注意双曲线的定义和正弦定理、余弦定理交汇解题；2、求双曲线方程需要两个独立条件．考点2 双曲线的简单几何性质【2-1】【2017北京，文10m =__________．【答案】2【解析】221,a b m == ，解得2m = .【2-2】【2018届广东省阳春市第一中学高三上第二次月考】若圆关于直线对称，则双曲线的离心率为（ ）A. B. C. D.【答案】C【解析】圆的半径为：，满足题意时，直线过圆心，即，双曲线的离心率为：.本题选择C选项.【2-3】【2017江苏，8】在平面直角坐标系中,双曲线的右准线与它的两条渐近线分别交于点,,其焦点是,则四边形的面积是 .【答案】【综合点评】1．已知渐近线方程y＝mx，若焦点位置不明确要分m＝ba或m＝ab讨论，求离心率值，需要寻求的等式，求离心率取值范围，需寻求关于的不等式关系，并结合求．2．注意数形结合思想在处理渐近线夹角，离心率范围求法中的应用．【领悟技法】1．双曲线的标准方程中对a、b的要求只是a＞0，b＞0易误认为与椭圆标准方程中a，b的要求相同．若a＞b＞0，则双曲线的离心率e∈(1，2)；若a＝b＞0，则双曲线的离心率e＝2；若0＜a＜b，则双曲线的离心率e＞ 2.2．注意区分双曲线中的a，b，c大小关系与椭圆a、b、c关系，在椭圆中a2＝b2＋c2，而在双曲线中c2＝a2＋b2.3．等轴双曲线的离心率与渐近线关系双曲线为等轴双曲线⇔双曲线的离心率e＝2⇔双曲线的两条渐近线互相垂直(位置关系)．4．双曲线的焦点到渐近线的距离等于虚半轴长b5．渐近线与离心率x2 a2－y2b2＝1(a>0，b>0)的一条渐近线的斜率为ba＝b2a2＝c2－a2a2＝e2－1.可以看出，双曲线的渐近线和离心率的实质都表示双曲线张口的大小．【触类旁通】【变式1】【2017课表1，文5】已知F是双曲线C P是C上一点，且PF与x轴垂直，点A的坐标是(1，3)，则△APF的面积为A B C D【答案】D【解析】【变式2】【2018届湖南省株洲市醴陵第二中学、醴陵第四中学高三上学期期中联考】已知双曲线E：﹣=1（a＞0，b＞0），点F为E的左焦点，点P为E上位于第一象限内的点，P关于原点的对称点为Q，且满足|PF|=3|FQ|，若|OP|=b，则E的离心率为（）A. B. C. 2 D.【答案】B【解析】由题意可知：双曲线的右焦点，由关于原点的对称点为则四边形为平行四边形则由，根据椭圆的定义在中，则，整理得则双曲线的离心率故答案选【综合点评】1、充分利用条件列关于的等式或不等式，可得离心率的取值或取值范围；2、双曲线的渐近线是与之间的比值关系，再结合，可得的关系，及离心率的关系，从这点而言，渐近线方程和离心率是有联系的．【易错试题常警惕】易错典例：已知圆，圆都内切于动圆，试求动圆圆心的轨迹方程．易错分析：忽视双曲线定义．正确解析：圆O2：，即为所以圆O 2的圆心为,半径,而圆的圆心为,半径,设所求动圆圆心M的坐标为(x,y),半径为r则且，所以且,点M的轨迹为双曲线右支，方程为．温馨提示：双曲线的轨迹类型是．【学科素养提升之思想方法篇】数形结合百般好，隔裂分家万事休——数形结合思想我国著名数学家华罗庚曾说过:"数形结合百般好，隔裂分家万事休。

课时作业 A 组 基础对点练1．(2017·合肥质检)若双曲线C 1：x 22－y 28＝1与C 2：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线相同，且双曲线C 2的焦距为45，则b ＝( ) A ．2 B ．4 C ．6D ．8解析：由题意得，ba ＝2⇒b ＝2a ，C 2的焦距2c ＝45⇒c ＝a 2＋b 2＝25⇒b ＝4，故选B. 答案：B2．(2017·广州联考)已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的焦距为10，点P (2,1)在C 的一条渐近线上，则C 的方程为( ) A.x 220－y 25＝1 B ．x 25－y 220＝1 C.x 280－y 220＝1D ．x 220－y 280＝1解析：依题意⎩⎪⎨⎪⎧a 2＋b 2＝25，1＝b a×2，解得⎩⎨⎧a 2＝20，b 2＝5，∴双曲线C 的方程为x 220－y 25＝1.答案：A3．已知双曲线x 24－y 2b 2＝1(b ＞0)的离心率等于33b ，则该双曲线的焦距为( ) A ．2 5 B ．2 6 C ．6D ．8解析：设双曲线的焦距为2c .由已知得c 2＝33b ，又c 2＝4＋b 2，解得c ＝4，则该双曲线的焦距为8. 答案：D4．已知双曲线9y 2－m 2x 2＝1(m ＞0)的一个顶点到它的一条渐近线的距离为15，则m ＝( )A ．1B ．2C ．3D ．4解析：依题意，双曲线的一个顶点为⎝ ⎛⎭⎪⎫0，13，一条渐近线的方程为mx －3y ＝0，则顶点到渐近线的距离为|－13×3|m 2＋9＝15，则m ＝4. 答案：D5．(2017·湖南六校联考)已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右焦点分别为F 1、F 2，以F 1F 2为直径的圆与双曲线渐近线的一个交点为(3,4)，则此双曲线的方程为( ) A.x 216－y 29＝1 B ．x 23－y 24＝1 C.x 29－y 216＝1D ．x 24－y 23＝1解析：由已知可得交点(3,4)到原点O 的距离为圆的半径，则半径r ＝32＋42＝5，故c ＝5，a 2＋b 2＝25，又双曲线的一条渐近线y ＝ba x 过点(3,4)，故3b ＝4a ，可解得b ＝4，a ＝3，故选C. 答案：C6．(2017·张掖诊断)如图，F 1、F 2分别是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右焦点，过F 1的直线l 与双曲线的左、右两支分别交于点B 、A .若△ABF 2为等边三角形，则双曲线的离心率为( )A.7 B ．4 C.233D ． 3解析：依题意得|AB |＝|AF 2|＝|BF 2|，结合双曲线的定义可得|BF 1|＝2a ，|BF 2|＝4a ，|F 1F 2|＝2c ，根据等边三角形，可知∠F 1BF 2＝120°，应用余弦定理，可得4a 2＋16a 2＋2·2a ·4a ·12＝4c 2，整理得c a ＝7，故选A.答案：A7．(2017·南昌调研)已知F 1，F 2是双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的两个焦点，P 是C 上一点，若|PF 1|＋|PF 2|＝6a ，且△PF 1F 2最小内角的大小为30°，则双曲线C 的渐近线方程是( ) A.2x ±y ＝0 B ．x ±2y ＝0 C ．x ±2y ＝0D ．2x ±y ＝0解析：由题意，不妨设|PF 1|＞|PF 2|，则根据双曲线的定义得， |PF 1|－|PF 2|＝2a ， 又|PF 1|＋|PF 2|＝6a ， 解得|PF 1|＝4a ，|PF 2|＝2a .在△PF 1F 2中，|F 1F 2|＝2c ，而c ＞a ，所以|PF 2|＜|F 1F 2|， 所以∠PF 1F 2＝30°，所以(2a )2＝(2c )2＋(4a )2－2×2c ×4a cos 30°， 得c ＝3a ，所以b ＝c 2－a 2＝2a ，所以双曲线的渐近线方程为y ＝±b a x ＝±2x ，即2x ±y ＝0.答案：A8．已知A 、B 分别为双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右顶点，点P 为双曲线C 在第一象限的任意一点，点O 为坐标原点，若双曲线C 的离心率为2，P A ，PB ，PO 的斜率分别为k 1，k 2，k 3，则k 1k 2k 3的取值范围为( ) A.⎝⎛⎭⎪⎫0，39B ．()0，3 C.()0，33D ．(0,8)解析：法一：因为e ＝c a ＝2，所以b ＝3a ，设P (x 0，y 0)(x 0＞0，y 0＞0)，则x 20a 2－y 20b 2＝1，k 1·k 2＝y 0x 0＋a ·y 0x 0－a ＝y 20x 20－a 2＝b 2a 2＝3，又双曲线的渐近线方程为y ＝±3x ，所以0＜k 3＜3，所以0＜k 1k 2k 3＜33，故选C.法二：由双曲线C 的离心率为2可取c ＝2，a ＝1，b ＝3，∴A (－1,0)，B (1,0)，设P (x 0，y 0)(x 0＞0，y 0＞0)，则x 20－y 203＝1，k 1k 2＝y 0x 0＋1·y 0x 0－1＝y 20x 20－1＝3，又双曲线的渐近线方程为y ＝±3x ，所以0＜k 3＜3，所以0＜k 1k 2k 3＜33，故选C. 答案：C9．(2017·开封模拟)已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)满足条件：(1)焦点为F 1(－5,0)，F 2(5,0)；(2)离心率为53，求得双曲线C 的方程为f (x ，y )＝0.若去掉条件(2)，另加一个条件求得双曲线C 的方程仍为f (x ，y )＝0，则下列四个条件中，符合添加条件的共有( )①双曲线C 上的任意点P 都满足||PF 1|－|PF 2||＝6； ②双曲线C 的虚轴长为4；③双曲线C 的一个顶点与抛物线y 2＝6x 的焦点重合； ④双曲线C 的渐近线方程为4x ±3y ＝0. A ．1个 B ．2个 C ．3个D ．4个解析：①由||PF 1|－|PF 2||＝6，得a ＝3，又c ＝5，所以离心率为53，①符合；②中b ＝2，c ＝5，a ＝21，此时离心率等于52121，②不符合；③中a ＝32，c ＝5，此时离心率等于103，也不符合；④渐近线方程为4x ±3y ＝0，所以b a ＝43，离心率为53，④符合．故选B. 答案：B10．(2017·沈阳质量监测)已知P 是双曲线x 23－y 2＝1上任意一点，过点P 分别作双曲线的两条渐近线的垂线，垂足分别为A ，B ，则P A →·PB →的值是( ) A ．－38 B ．316 C ．－38D ．不能确定解析：设P (x 0，y 0)，因为该双曲线的渐近线分别是x 3－y ＝0，x3＋y ＝0，所以可取|P A |＝|x 03－y 0|13＋1，|PB |＝|x 03＋y 0|13＋1，又cos ∠APB ＝－cos ∠AOB ＝－cos 2∠AOx＝－cos π3＝－12，所以P A →·PB →＝|P A →|·|PB →|·cos ∠APB ＝|x 203－y 20|43·⎝ ⎛⎭⎪⎫－12＝34×(－12)＝－38，选A. 答案：A11．(2017·武汉武昌区调研)双曲线Γ：y 2a 2－x 2b 2＝1(a ＞0，b ＞0)的焦距为10，焦点到渐近线的距离为3，则Γ的实轴长等于__________．解析：双曲线的焦点(0,5)到渐近线y ＝ab x ，即ax －by ＝0的距离为|5b |a 2＋b2＝5bc ＝b ＝3，所以a ＝4,2a ＝8. 答案：812．若双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一个焦点到一条渐近线的距离等于焦距的14，则该双曲线的离心率为________．解析：双曲线的一条渐近线方程为bx －ay ＝0，一个焦点坐标为(c,0)．根据题意得|bc －a ×0|b 2＋a 2＝14×2c ，所以c ＝2b ，a ＝c 2－b 2＝3b ，所以e ＝c a ＝23＝233. 答案：23313．已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)与椭圆x 29＋y 24＝1有相同的焦点，且双曲线C 的渐近线方程为y ＝±2x ，则双曲线C 的方程为________．解析：易得椭圆的焦点为(－5，0)，(5，0)，∴⎩⎪⎨⎪⎧a 2＋b 2＝5，b a ＝2，∴a 2＝1，b 2＝4，∴双曲线C 的方程为x 2－y 24＝1.答案：x 2－y 24＝114．过双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左焦点F 作圆x 2＋y 2＝a 2的两条切线，记切点分别为A 、B ，双曲线的左顶点为C ，若∠ACB ＝120°，则双曲线的离心率e ＝________.解析：连接OA ，根据题意以及双曲线的几何性质，|FO |＝c ，|OA |＝a ，而∠ACB ＝120°，∴∠AOC ＝60°，又F A 是圆O 的切线，故OA ⊥F A ，在Rt △F AO 中，容易得到|OF |＝2a ，∴e ＝ca ＝2. 答案：2B 组 能力提速练1．(2016·高考天津卷)已知双曲线x 24－y 2b 2＝1(b ＞0)，以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A ，B ，C ，D 四点，四边形ABCD 的面积为2b ，则双曲线的方程为( ) A.x 24－3y 24＝1 B ．x 24－4y 23＝1 C.x 24－y 24＝1D ．x 24－y 212＝1解析：利用双曲线方程写出圆和渐近线的方程，利用交点求出四边形边长即可表示出面积，解方程求b 即可．由题意知双曲线的渐近线方程为y ＝±b2x ，圆的方程为x 2＋y 2＝4，联立⎩⎪⎨⎪⎧x 2＋y 2＝4，y ＝b 2x ，解得⎩⎪⎨⎪⎧x ＝44＋b 2，y ＝2b4＋b 2，或⎩⎪⎨⎪⎧x ＝－44＋b 2，y ＝－2b4＋b 2，即第一象限的交点为⎝ ⎛⎭⎪⎫44＋b2，2b 4＋b 2. 由双曲线和圆的对称性得四边形ABCD 为矩形，其相邻两边长为84＋b 2，4b 4＋b2，故8×4b 4＋b 2＝2b ，得b 2＝12. 故双曲线的方程为x 24－y 212＝1.故选D. 答案：D2．(2016·高考浙江卷改编)已知椭圆C 1：x 2m 2＋y 2＝1(m ＞1)与双曲线C 2：x2n 2－y 2＝1(n ＞0)的焦点重合，e 1，e 2分别为C 1，C 2的离心率，则( ) A ．m ＞n 且e 1e 2＞1 B ．m ＞n 且e 1e 2＜1 C ．m ＜n 且e 1e 2＞1 D ．m ＜n 且e 1e 2＜1解析：先利用两圆锥曲线的焦点相同，求出字母之间的关系，再求解离心率之积的取值范围．C 1的焦点为(±m 2－1，0)，C 2的焦点为(±n 2＋1，0)， ∵C 1与C 2的焦点重合，∴m 2－1＝n 2＋1，∴m 2＝n 2＋2，∴m 2＞n 2. ∵m ＞1，n ＞0，∴m ＞n .∵C 1的离心率e 1＝m 2－1m ，C 2的离心率e 2＝n 2＋1n ， ∴e 1e 2＝m 2－1m ·n 2＋1n ＝(m 2－1)(n 2＋1)mn＝(m 2－1)(n 2＋1)m 2n 2＝(n 2＋1)2(n 2＋2)n 2＝n 4＋2n 2＋1n 4＋2n 2＞1＝1.答案：A3．(2017·江西联考)已知F 1，F 2分别是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左，右焦点，若在双曲线的右支上存在一点M ，使得(OM →＋OF 2→)·F 2M →＝0(其中O 为坐标原点)，且|MF 1→|＝3|MF 2→|，则双曲线的离心率为( ) A.5－1 B ．3＋12 C.5＋12D ．3＋1解析：∵F 2M →＝OM →－OF 2→，∴(OM →＋OF 2→)·F 2M →＝(OM →＋OF 2→)·(OM →－OF 2→)＝0，即OM →2－OF 22→＝0，∴|OF 2→|＝|OM →|＝c ，在△MF 1F 2中，边F 1F 2上的中线等于|F 1F 2|的一半，可得MF 1→⊥MF 2→.∵|MF 1|→＝3|MF 2→|，∴可设|MF 1→|＝3λ，|MF 2→|＝λ(λ＞0)，得(3λ)2＋λ2＝4c 2，解得λ＝c ，∴|MF 1→|＝3c ，|MF 2→|＝c ，∴根据双曲线定义得2a ＝|MF 1→|－|MF 2→|＝(3－1)c ，∴双曲线的离心率e ＝2c 2a ＝3＋1. 答案：D4．(2016·高考北京卷)双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝________.解析：不妨令B 为双曲线的右焦点，A 在第一象限，则双曲线如图所示． ∵四边形OABC 为正方形，|OA |＝2， ∴c ＝|OB |＝22，∠AOB ＝π4. ∵直线OA 是渐近线，方程为y ＝ba x ，∴ba ＝tan ∠AOB ＝1，即a ＝b . 又∵a 2＋b 2＝c 2＝8，∴a ＝2. 答案：25．(2016·高考浙江卷改编)设双曲线x 2－y 23＝1的左、右焦点分别为F 1，F 2.若点P 在双曲线上，且△F 1PF 2为锐角三角形，求|PF 1|＋|PF 2|的取值范围． 解析：∵双曲线x 2－y 23＝1的左、右焦点分别为F 1，F 2，点P 在双曲线上，∴|F 1F 2|＝4，||PF 1|－|PF 2||＝2.若△F 1PF 2为锐角三角形，则由余弦定理知|PF 1|2＋|PF 2|2－16＞0，可化为(|PF 1|＋|PF 2|)2－2|PF 1|·|PF 2|＞16①.由||PF 1|－|PF 2||＝2，得(|PF 1|＋|PF 2|)2－4|PF 1||PF 2|＝4.故2|PF 1||PF 2|＝(|PF 1|＋|PF 2|)2－42，代入不等式①可得(|PF 1|＋|PF 2|)2＞28，解得|PF 1|＋|PF 2|＞27.不妨设P 在左支上，∵|PF 1|2＋16－|PF 2|2＞0，即(|PF 1|＋|PF 2|)·(|PF 1|－|PF 2|)＞－16，又|PF 1|－|PF 2|＝－2，∴|PF 1|＋|PF 2|＜8.故27＜|PF 1|＋|PF 2|＜8.。

2018年高考数学讲练测【浙江版】【测】第九章 解析几何第六节 双曲线班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的．）1。

【2018届广雅中学、东华中学、河南名校高三上学期第一次联考】双曲线x 2a 2−y 24a 2=1(a ≠0)的渐近线方程为（ ）A. y =±2xB. y =±12x C 。

y =±4x D. y =±√2x【答案】A【解析】根据双曲线的渐近线方程知，y =±2a a x =±2x ，故选A.2。

【2018届云南省昆明一中高三第一次摸底】已知双曲线C 的中心为原点，点()2,0F 是双曲线C 的一个焦点，点F 到渐近线的距离为1，则C 的方程为（ ) A.221x y -=B.2212y x -= C 。

22123x y -= D.22133x y -= 【答案】A3。

【2018届辽宁省凌源二中高三三校联考】已知双曲线()222:1016x y C a a -=>的一个焦点为()5,0,则双曲线C 的渐近线方程为（ ）A 。

4312x y ±= B.4410x y ±=C. 1690x y ±=D. 430x y ±=【答案】D【解析】由题得c=5,则22169ac =-= ，即a=3,所以双曲线的渐近线方程为43y x =± ，即430x y ±= ，故选D4。

【2018届云南省昆明市高新技术开发区高考适应性月考】已知双曲线22221x y a b-=（0,0a b >>）的一条渐近线方程为32y x =，且双曲线的一个焦点在抛物线247y x =-的准线上，则双曲线的方程为（ ) A.22143x y -= B 。