30度45度60度三角函数

三角函数30度60度45度顺口溜巧记三角函数定义：初中所学的三角函数有正弦、余弦、正切、余切，它们实际是三角形边的比值，可以把两个字用／隔开，再用下面的一句话记定义：一位不高明的厨子教徒弟杀鱼，说了这么一句话:正对鱼磷(余邻)直刀切。

正：正弦或正切，对：对边即正是对；余：余弦或余弦，邻：邻边即余是邻；切是直角边。

三角函数的增减性：正增余减
特殊三角函数值记忆:首先记住30度、45度、60度的正弦值、余弦值的分母都是2、正切、余切的分母都是3，分子记口诀“123，321，三九二十七”既可。

平行四边形的判定：要证平行四边形，两个条件才能行，一证对边都相等，或证对边都平行，一组对边也可以，必须相等且平行。

对角线，是个宝，互相平分“跑不了”，对角相等也有用，“两组对角”才能成。

梯形问题的辅助线：移动梯形对角线，两腰之和成一线；平行移动一条腰，两腰同在“△”现；延长两腰交一点，“△”中有平行线；作出梯形两高线，矩形显示在眼前；已知腰上一中线，莫忘作出中位线。

添加辅助线歌：辅助线，怎么添？找出规律是关键，题中若有角（平）分线，可向两边作垂线；线段垂直平分线，引向两端把线连，三角形边两中点，连接则成中位线；三角形中有中线，延长中线翻一番。

三角函数30度60度45度90度三角函数是数学中的一种特殊函数，它与三角形的边长和角度之间的关系密切相关。

在三角函数中，最常见的角度包括30度、60度、45度和90度。

本文将从这四个角度出发，介绍三角函数的基本概念和性质。

一、30度30度是一个特殊的角度，它是一个锐角，小于90度。

在三角函数中，30度对应的正弦值、余弦值和正切值都有特定的数值。

正弦函数（sin）是指一个角的对边与斜边的比值，而30度的正弦值为1/2。

余弦函数（cos）是指一个角的邻边与斜边的比值，30度的余弦值为√3/2。

正切函数（tan）是指一个角的对边与邻边的比值，30度的正切值为√3/3。

二、60度60度也是一个锐角，它是30度的补角，即两个角的和为90度。

与30度类似，60度对应的正弦、余弦和正切值也有特定的数值。

正弦函数是指一个角的对边与斜边的比值，60度的正弦值为√3/2。

余弦函数是指一个角的邻边与斜边的比值，60度的余弦值为1/2。

正切函数是指一个角的对边与邻边的比值，60度的正切值为√3。

三、45度45度是一个特殊的角度，它是一个直角三角形的两个锐角相等的角度。

在三角函数中，45度对应的正弦、余弦和正切值同样有特定的数值。

正弦函数是指一个角的对边与斜边的比值，45度的正弦值为√2/2。

余弦函数是指一个角的邻边与斜边的比值，45度的余弦值为√2/2。

正切函数是指一个角的对边与邻边的比值，45度的正切值为1。

四、90度90度是一个特殊的角度，它是一个直角，也是一个补角为零度的角度。

在三角函数中，90度的正弦值、余弦值和正切值都有特定的数值。

正弦函数是指一个角的对边与斜边的比值，90度的正弦值为1。

余弦函数是指一个角的邻边与斜边的比值，90度的余弦值为0。

正切函数是指一个角的对边与邻边的比值，90度的正切值为无穷大。

三角函数30度、60度、45度和90度分别对应着不同的正弦、余弦和正切值。

它们在三角函数的研究和应用中起着重要的作用。

特殊角的三角函数值公式大全三角函数是数学中一类基础且重要的函数，它们在几何、物理、工程等各个领域都有着广泛的应用。

在三角函数中，特殊角所对应的三角函数值往往是我们熟知的，今天我们来总结一下特殊角的三角函数值公式。

正弦函数值正弦函数是一种常见的三角函数，用于表示直角三角形中的对边与斜边之比。

对于特殊角来说，它们的正弦函数值是固定的，常见的特殊角有0度、30度、45度、60度和90度。

下面是它们的正弦函数值公式：•正弦0度：sin(0) = 0•正弦30度：sin(30) = 1/2•正弦45度：sin(45) = √2/2•正弦60度：sin(60) = √3/2•正弦90度：sin(90) = 1余弦函数值余弦函数也是一种常见的三角函数，用于表示直角三角形中的邻边与斜边之比。

特殊角的余弦函数值也是固定的，和正弦函数值相似，下面是特殊角的余弦函数值公式：•余弦0度：cos(0) = 1•余弦30度：cos(30) = √3/2•余弦45度：cos(45) = √2/2•余弦60度：cos(60) = 1/2•余弦90度：cos(90) = 0正切函数值正切函数是三角函数中的另一个重要函数，它表示直角三角形的对边与邻边之比。

正切函数的特殊角值也是固定的，下面是特殊角的正切函数值公式：•正切0度：tan(0) = 0•正切30度：tan(30) = √3/3•正切45度：tan(45) = 1•正切60度：tan(60) = √3•正切90度：tan(90) = 无穷大总结通过以上内容，我们总结了特殊角的正弦、余弦和正切函数值公式，这些特殊角值在数学计算中应用非常广泛，能够帮助我们解决各种问题。

熟练掌握这些特殊角的三角函数值公式，将对我们理解和运用三角函数起到很大的帮助。

希望本文对特殊角的三角函数值公式有一个清晰的了解，也希望读者能够在学习和工作中充分利用这些知识，提高数学应用能力。

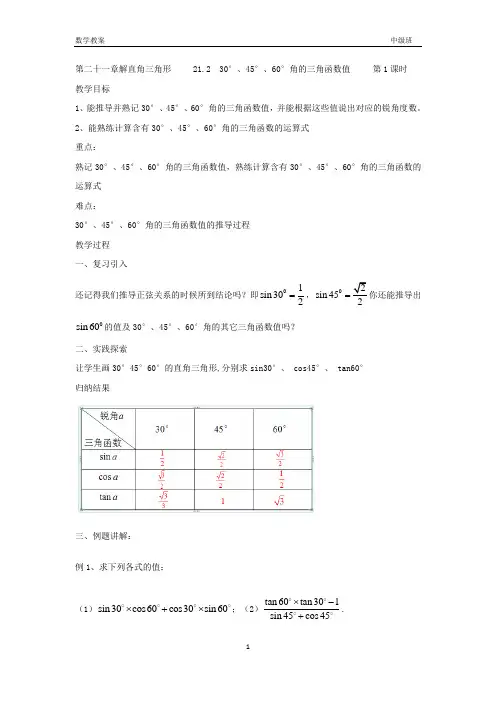
第二十一章解直角三角形 21.2 30°、45°、60°角的三角函数值 第1课时 教学目标1、能推导并熟记30°、45°、60°角的三角函数值，并能根据这些值说出对应的锐角度数。

2、能熟练计算含有30°、45°、60°角的三角函数的运算式 重点：熟记30°、45°、60°角的三角函数值，熟练计算含有30°、45°、60°角的三角函数的运算式 难点：30°、45°、60°角的三角函数值的推导过程 教学过程 一、复习引入还记得我们推导正弦关系的时候所到结论吗？即01sin 302=，0sin 452=你还能推导出0sin 60的值及30°、45°、60°角的其它三角函数值吗？二、实践探索让学生画30°45°60°的直角三角形,分别求sin30°、 cos45°、 tan60° 归纳结果三、例题讲解：例1、求下列各式的值：（1）sin30cos60cos30sin 60⨯+⨯；（2）tan 60tan 301sin 45cos 45⨯-+.例2、求适合下列条件的锐角α：10α-=; (2)2cos 112α+=; (3) 3tan α=注意：互余两角的三角函数关系（A 为锐角）：SinA=cos(90°-A)，即一个锐角的正弦值等于它的余角的余弦值；cosA=sin(90°-A)，即一个锐角的余弦值等于它的余角的正弦值.四、随堂练习：1、计算下列各式的值：（1）2tan30sin 45cos60+-； （2）22sin 30cos 30+；（3）1tan 601tan 30-+； （4）tan 45sin 30cos30tan 30++.2、求适合下列条件的锐角α：10α-=; (2) 3tan 0α=; (3) 3α=.五、拓展提高：1、求下列各式的值：（1）02245sin 30sin 245cos 60cos ++ （2）00000000cos60sin 45cos60cos 45cos60sin 45sin 30cos 45+-+-+解 （1）原式=22212222122⨯⨯+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛45212141=++=（2）原式=22321212221222122212221--=-+=+-+-+说明：本题主要考查特殊角的正弦余弦值，解题关键是熟悉并牢记特殊角的正弦余弦值。

特殊的三角函数值表30,45,60
三角函数把一个角度转换成一个“比率”，它可以告诉我们那个角度的正切值、余切值和正弦值等等，是计算和研究它们之间关系的关键技术手段，是构成计算机科学领域的重要内容，其研究活动以大数据技术为基础，通过对数据的分析总结，开发出多种特殊的三角函数值表。

特殊的三角函数值表，一般有30°、45°、60°几种。

30°是角度最小的，
其正切值为0.577，余切值为1.732，正弦值为0.5，其余两个角度的正切值均小
于该值，而余切值都大于1.732；45°正切值为1，余切值等于1，正弦值为0.707，在此值的基础上，60°的值就大于45°的，但是小于1，而余切值也大于1。

三角函数值表是应用大数据处理技术来总结数据的重要技术工具，在很多计算
器的设计中得到了广泛的应用，并且把特殊的三角函数值表作为标准进行开发，它能够帮助社会上人们解决一些日常生活中涉及到三角函数的问题，比如在工业自动化控制中，三角函数也常常被应用到做一些快速的计算，提高效率，如今，随着技术的发展和新颖的理论出现，特殊的三角函数值表也会不断丰富，为人们解决问题提供了一种新的思路。