自由模态和约束模态
- 格式:docx
- 大小:15.01 KB
- 文档页数:2

最近在做结构的模态分析,查找了很多论坛,资料也翻了很多。
有人说这个要做自由模态分析,因为它理论上代表了结构的全部振型才有参考价值,也有人说,模态分析要看具体的边界条件,自由模态中出现的振型不肯定会在约束模态中出现,因此要依据实际情况来决定是否用自由模态分析还是约束模态分析。
乍看,两种说法都有道理。
可是想做模态分析来猎取有用信息的人糊涂了,因为这两种情况下算的频率值不仅有区别,而且算的值通常差异还很大!那么到底该听谁的呢?好了,不绕关子了。
问题就出现在实际与理论的差异上!倾向于做自由模态分析的人偏理论,因为自由模态分析实在可以得到全部结构振型。
而倾向于约束模态分析的人太倾向于实际。
认为约束的就应该按约束的算。
好吧,问题就出在这了,虽然一般来说,约束关系根本是明确的,但是其复杂程度不是我们可以预料到的,由于有限元分析的简化假设,对于约束,尤其是复杂构件的约束我们很难建立其真正的边界条件,那么我们所谓的边界约束也就无从谈起,如贸然采纳刚性连接等作为约束,无形中增加了结构的刚度〔这也是我们很多人在做约束模态分析时得到的值比自由模态分析时高的原因之一〕,但是这个刚度增加的X谁也说不清楚。
所以,我建议的措施是,对于复杂的约束难以确立的构件,倒不如用自由模态分析,起码还能在其中选择我们关怀的振型。
可是,如果对复杂件做某些约束下的约束模态分析,我们是无法获知其在其他约束下〔有可能正是这个才是真正的约束呢〕的振型,那样我们将得不偿失,有时候还会得到错误的结果。
实在是貌似有道理,但要挑出我们需要的那几阶模态谈何简单。
我以前老师的看法就是必须加约束算模态。
做模态分析是为我们分析系统的动力响应提供方便,系统的动力响应是肯定要满足约束条件的。
如果我们做自由模态分析,求出全部模态后,要挑出那些满足约束的模态来是要费很大的劲的。
实际应用中的自由度动辄上万,约束也很复杂。
而且我们曾经从理论上证明过,约束的存在只是去掉了那些不满足约束条件的模态,但其他的模态是没影响的。
一、CA TIA有限元分析学习基础如学习实体零件有限元分析,应当先学习零件创建相关模块,如part design零部件设计;如学习车身零件有限元分析,应当先学习曲面创建、零件创建相关模块如wireframe and surface Design 线框和曲面设计,generative shape design创成式外形设计。
如学习总成有限元分析,应当先学习assembly design装配件设计还需要熟悉catia一般操作,如放大缩小旋转平移。
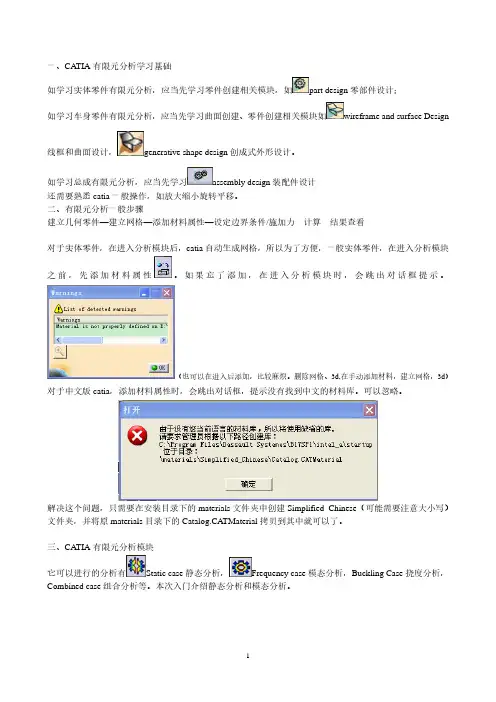
二、有限元分析一般步骤建立几何零件—建立网格—添加材料属性—设定边界条件/施加力---计算---结果查看对于实体零件,在进入分析模块后,catia自动生成网格,所以为了方便,一般实体零件,在进入分析模块之前,先添加材料属性。
如果忘了添加,在进入分析模块时,会跳出对话框提示。
(也可以在进入后添加,比较麻烦。
删除网格、3d,在手动添加材料,建立网格,3d)对于中文版catia,添加材料属性时,会跳出对话框,提示没有找到中文的材料库。
可以忽略。
解决这个问题,只需要在安装目录下的materials文件夹中创建Simplified_Chinese(可能需要注意大小写)文件夹,并将原materials目录下的Catalog.CA TMaterial拷贝到其中就可以了。
三、CA TIA有限元分析模块它可以进行的分析有Static case静态分析,Frequency case模态分析,Buckling Case挠度分析,Combined case组合分析等。
本次入门介绍静态分析和模态分析。
四、界面介绍-------------------------------------------------------------- 1、model manager模型管理2、loads 载荷3、restraints 约束4、compute计算5、image云图6、analysis tools 分析工具--------------------------------------------------------------------------- 7、analysis supports连接支持8、connection propertis连接属性9、virtual parts虚拟零件10、网格规范11、Groups群组12、计算存储处理13、material on analysis connection 连接支持的材料14、modulation 模态15、analysis assembly 2d viewer 分析总成结构树分析文件的结构五、入门命令创建四面体网格,用于3D体单元网格划分。


发信人: laissez (中正平和), 信区: DeptMech标题: 《振动力学》名词中英文对照发信站: 碧海青天(Tue Dec 12 16:06:09 2000), 转信Dirac delta function delta函数acceleration加速度admittance导纳amplification factor动力放大因子amplitude幅值、振幅amplitude-frequency characteristic幅频特性angular frequency圆频率attenuation vibration衰减振动base motion基础运动bending vibration弯曲振动boundary condition边界条件chaotic vibration混沌振动complementary energy余能complex frequency response function复频响应函数component modal synthesis method模态综合法condition of orthogonality正交性条件conservative system保守系统consistent mass matrix一致(协调)质量阵constraint mode约束模态continuous system连续系统continuum连续体damping coefficient阻尼系数damping ratio阻尼比damping vibration有阻尼振动degree-of-freedom自由度differential equation of motion动力学微分方程direct numerical integration直接积分法discrete system离散系统displacement位移dissipative system耗散系统Duhamel integral杜哈曼积分dynamical matrix动力矩阵dynamical system动力学系统dynamics动力学eigenvalue特征值eigenvector特征向量element单元energy of deformation变形能excitation激励flexibility柔度forced vibration强迫振动foundation基础Fourier transformation傅氏变换free vibration自由振动frequency equation频率方程fundamental frequency基频general coordinate广义坐标general solution通解generalized eigenvalue problem广义特征值问题governing equation控制方程impulse response function脉冲响应函数inertia惯性initial condition初始条件kinetic energy动能logarithmic decrement对数衰减率longitudinal vibration纵向振动lumped mass method集中质量法mass matrix质量矩阵matrix iteration method矩阵迭代法mechanical energy机械能modal matrix振型矩阵mode振型、模态mode function振型函数mode superposition method振型叠加法mode truncation method振型截断法natural frequency固有频率negative damping负刚度node节点normal mode简正振型oscillation振动、振荡period周期phase angle相角phase difference相位差positive definite正定potential energy势能principal mass主质量principal stiffness主刚度principle of superposition迭加原理principle of virtual work虚功原理proportional damping比例阻尼Rayleigh quotient瑞利商reduced mass约化质量resonance共振restoring force恢复力rotation转动shape function形函数shear vibration剪切振动shift frequency method移轴法simple harmonic excitation简谐激励spring-mass system弹簧-质量系统stability稳定性steady-state response稳态响应steady-state solution稳态解stiffness matrix刚度矩阵strain energy应变能structural damping结构阻尼subspace iteration method子空间迭代法system系统torsional vibration扭转振动transient solution瞬态解translation平动transverse vibration横向振动trial function试函数undamped vibration无阻尼振动variation变分velocity速度vibration振动viscous damping粘性阻尼。


PATRAN的一些精华小技巧1、在Patran里如何Move 一组Points 的位置, 而不改变这组Points 的ID 编号? Group/Transform/Translate的功能,这样不但编号不会变, 连property跟边界条件都会保留2、Patran如何执行多次Undo?所有Patran的操作步骤, 都记录在最新的一个patran.ses.xx中,如果需要多次undo, 可以刪除最后不需要的步骤指令行,再利用File -> Session -> Play 的方式, 执行改过的patran.ses.xx ,这样可以无限制的undo。
3、Patran中如何定义杆件之间的铰接?用的是rod元素,不需要定义铰接,因为rod元间本身就是以铰接形式连接。
如果用bar或是beam,需在properties里的Pinned DOFs @ Node 1/2定义铰接。
4、Patran 如何把不小心Equivalence的node分开用Utility/FEM-Elements/Separate Elements在equivalence时, 可以將选项切换为"List",只选择特定某些节点作equivalence, 可以避免不小心的失誤。
5、Patran如何將Tri3单元转换为Tri6单元在Patran -> Element -> Modify/Element/Edit , 將Type选项打勾,在Shape中选Tri, New Shape 选Tri6, 最后选取想要改变的Tri3单元,6、Patran 如何定义材料库Patran除了可以直接读取MSC.Mvision的材料材料库外,还可利用执行Session File的方式,直接使用以前已经定义过的材料。
编辑patran.ses.xx,将定义材料的PCL指令剪下,粘贴到另外一个文件中(如mat.ses)。
之后便可直接由Patran的File/ Session/ Play来加入此一材料的定义。
一、CATIA有限元分析学习基础如学习实体零件有限元分析,应当先学习零件创建相关模块,如part design零部件设计;如学习车身零件有限元分析,应当先学习曲面创建、零件创建相关模块如wireframe and surface Design线框和曲面设计,generative shape design创成式外形设计。
如学习总成有限元分析,应当先学习assembly design装配件设计还需要熟悉catia一般操作,如放大缩小旋转平移。
二、有限元分析一般步骤建立几何零件—建立网格—添加材料属性—设定边界条件/施加力---计算---结果查看对于实体零件,在进入分析模块后,catia自动生成网格,所以为了方便,一般实体零件,在进入分析模块之前,先添加材料属性。
如果忘了添加,在进入分析模块时,会跳出对话框提示。
(也可以在进入后添加,比较麻烦。
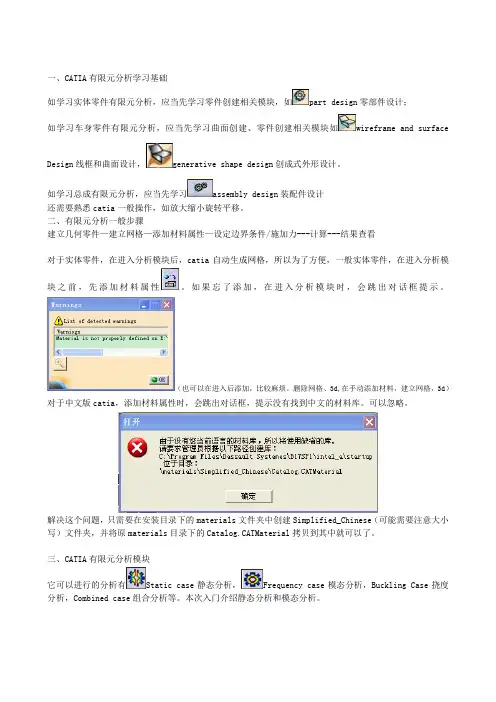
删除网格、3d,在手动添加材料,建立网格,3d)对于中文版catia,添加材料属性时,会跳出对话框,提示没有找到中文的材料库。
可以忽略。
解决这个问题,只需要在安装目录下的materials文件夹中创建Simplified_Chinese(可能需要注意大小写)文件夹,并将原materials目录下的Catalog.CATMaterial拷贝到其中就可以了。
三、CATIA有限元分析模块它可以进行的分析有Static case静态分析,Frequency case模态分析,Buckling Case挠度分析,Combined case组合分析等。
本次入门介绍静态分析和模态分析。
四、界面介绍-------------------------------------------------------------- 1、model manager模型管理2、loads 载荷3、restraints 约束4、compute计算5、image云图6、analysis tools 分析工具--------------------------------------------------------------------------- 7、analysis supports连接支持8、connection propertis连接属性9、virtual parts虚拟零件10、网格规范11、Groups群组12、计算存储处理13、material on analysis connection 连接支持的材料14、modulation 模态15、analysis assembly 2d viewer 分析总成结构树分析文件的结构五、入门命令创建四面体网格,用于3D体单元网格划分。
网上经常看到一些朋友询问关于自由模态与约束模态的问题,而且看到了很多不同的说法。
而最近又有朋友向我问到了这个问题,我想,还是彻底地解决这个问题为好。
而要彻底解决它,就需要考察其理论基础。
所以这篇文章专门去看看它的理论底层。
首先我们要明确,无论是自由模态还是约束模态,都属于模态分析的范畴。
那么什么是模态分析呢?这个概念来自于《机械振动》。
于是我们到《机械振动》中去看看。
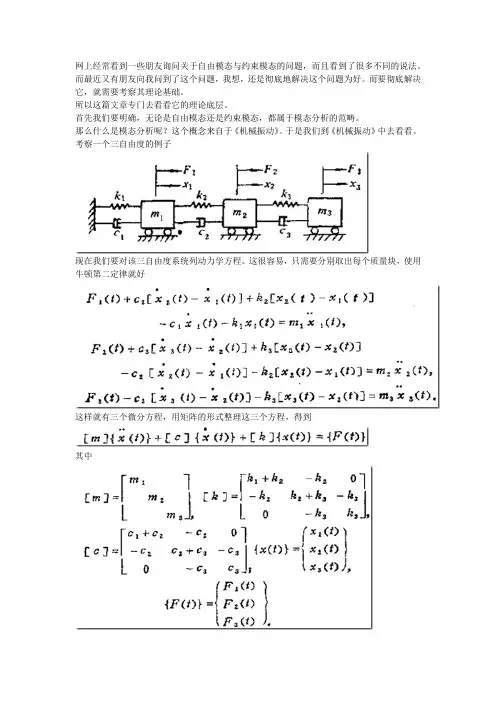
考察一个三自由度的例子现在我们要对该三自由度系统列动力学方程。
这很容易,只需要分别取出每个质量块,使用牛顿第二定律就好这样就有三个微分方程,用矩阵的形式整理这三个方程,得到其中这里的[m][k][c]分别是质量矩阵,刚度矩阵和阻尼矩阵。
而{F(t)}是力向量。
下面我们来考虑模态分析。
所谓模态分析,是取力向量为0,就是说系统不受外力;而且忽略阻尼,则上述方程变成下面的任务是求解这个微分方程组这种解很难找到,于是我们假设了一个解的形式为(很有意思的是,这种形式的解刚好是正确的)将该假设的解代入到上述方程中,得到整理上述方程组,得到该方程组的左边只与时间t有关,而右边与时间t无关。
如果要这两边相等,除非两端都等于一个常数。
例如都等于,于是有(1)以及(2)对于(1)式,从《高等数学》的二阶常系数微分方程的解可以知道,其解为对于(2)式,把它写成矩阵形式,并令可以得到提出位移向量{u},可以得到上述式子要有非零解,按照《线性代数》理论,有将该式子展开,可以得到根据它就可以解出各个可以证明,该方程有n个正实根,它们对应于系统的n个自然频率。
假设没有重根,则这些频率可以从小到大排序,得到这其中,最小的这个就是基频。
可见,系统有多少个自由度,就有多少个频率。
在解出所有频率后,将某个频率代入到中,就可以得到此时的此即系统的模态向量或者振型向量。
从以上推导中我们知道(1)有多少个自由度,就有多少个自然频率。
(2)有多少个自然频率,就有多少个与自然频率相对应的模态向量。

某乘用车塑料背门NVH性能分析与研究杨万江【摘要】随着节能和环保问题的日益突出,汽车轻量化技术的研究逐渐成为现代汽车设计的热点.为了探究塑料背门对汽车振动噪声性能的影响,保证乘坐舒适性,首先对塑料背门进行自由模态分析和整车状态下的约束模态分析,并与金属背门进行对比,两者模态频率接近,振型一致.再进行声腔模态分析,发现塑料背门第一阶约束模态与声腔模态明显避频.最后在声密性测试的基础上进行整车NVH性能分析,结果表明,在匀速和2档全负荷加速工况下车内声压级相当,语音清晰度甚至高于金属背门,满足NVH性能要求.【期刊名称】《汽车实用技术》【年(卷),期】2017(000)019【总页数】4页(P132-135)【关键词】塑料背门;模态分析;NVH性能【作者】杨万江【作者单位】中国汽车工程研究院股份有限公司,重庆 401122【正文语种】中文【中图分类】U467.4+93CLC NO.: U 467.4+93 Document Code: A Article ID: 1671-7988 (2017)19-132-04随着汽车技术的不断进步和汽车工业的快速发展,汽车已经成为人们日常生活的重要部分,汽车在给人们带来诸多便利的同时,也存在能源、环保、安全和舒适等问题。
且随着能源与环境问题的日益突出,汽车轻量化技术的发展和应用逐渐被重视。
汽车轻量化技术综合考虑减重、节能、环保等因素,在保证汽车综合性能的前提下,使用新材料或新方法对汽车部件进行优化设计,尽可能降低汽车部件的自重[1-4]。
车身轻量化可通过使用如高强钢、铝合金、工程塑料等轻量化材料实现[5]。
其中,塑代钢不仅能实现车身轻量化,所用的塑料还能在汽车报废后实现回收再利用,避免资源浪费,减少环境污染,同时,汽车的舒适度、安全性和设计的灵活性也在一定程度上得到改善[6]。
近年来,国内外学者对汽车轻量化技术做了大量研究,如LGFPP 用10 mm左右的玻纤增强的聚丙烯材料,被广泛用于一些著名品牌汽车的前端模块和散热风扇中[7]。


基于ANSYS的发动机缸体模态分析文章以某四缸发动机缸体为研究对象,采用ANSYS软件进行模态分析。
首先在UG软件中建立发动机缸体的三维实体简化模型;然后将发动机缸体的模型导入ANSYS软件中划分网格;最后采用自由模态方式进行分析,获得发动机缸体的各阶固有频率和振型,分析发动机工作时外在激励对缸体的影响,为发动机缸体的优化设计和动力学分析提供理论依据。
标签:发动机缸体;实体模型;有限元;模态分析;振型1 概述发动机缸体是构成发动机的基体,起着保证发动机的动能产生和动力输出的作用。
发动机工作过程中,缸体承受着气缸内混合气燃烧所产生的爆发力、活塞连杆往复运动惯性力等周期性的载荷,这些载荷形成周期性激励。
发动机缸体质量较大,振动时对整车的影响也较大。
为了防止周期性的激励引起发动机缸体的共振,需要获得其固有频率和振型,从而在设计时避开外在激励频率,因此有必要因此有必要分析发动机缸体的模态。
典型的无阻尼模态分析是经典的特征值求解问题[1]:式中,K-刚度矩阵;?啄i-第i阶模态的特征向量;Wi-第i阶模态的固有频率;M-质量矩阵。
发动机缸体为铸造的箱体类零件,其表面上分布着各种凸台、加强筋和轴承孔,内部有气缸套、水套、油道孔和一些纵、横隔板等,结构很复杂,无法用单一的数学模型进行模态分析。
随着计算机硬件和软件技术的发展,采用计算机进行有限元分析已经成为一种切实有效的方法。
ANSYS是一种通用工程有限元分析软件,广泛应用于汽车、机械、电子、航空航天等各种领域[2]。
虽然ANSYS软件具有强大的有限元分析功能,但其几何建模功能相对较弱,在ANSYS软件中对复杂的发动机缸体建模相当困难。
因此,本文先在三维建模软件Unigraphics(以下简称UG)中建立发动机缸体的三维实体模型,然后导入ANSYS中进行模态分析。
2 发动机缸体实体模型本文以某四缸柴油机缸体为研究对象。
建立有限元模型时,理论上应详细表达缸体结构特征以准确分析,但模型过于复杂会导致难以计算,因此有必要对缸体模型进行简化。
⾃由模态分析和约束模态分析的区别1。
⾃由和约束模态分析只是边界条件不同的两种模态分析⽽已;2。
在实际⼯程问题中,⾃由和约束两种边界条件均⼴泛存在,如飞机、⽕箭、导弹等为⾃由边界条件,⽽机床架、⾼层建筑等为约束边界。
3。
解决⼯程问题的最终有限元模型分析应与⼯程实际的边界条件相同(或向近似)!如飞机⽤⾃由模态分析其动⼒学稳定问题,以便确定飞⾏品质。
机床架⽤约束模态分析其动响应问题。
4。
但有限元模型不是凭空⽽来的,更不是⼀经建⽴便与实际结构固有特性相吻合,它必须是建⽴在结构设计数据和结构试验数据基础之上的。
其模型修改过程的模态分析⽅式应与试验边各界条件相吻合或近似(在满⾜⼯程精度的前提下)。
5。
⼀般⽽⾔,试验边界条件与⼯程实际边界应该相同。
但在有些情况下,也不尽相同!如超⼤型飞机A380、超⼤的⽕箭、飞船要实现⾃由条件的试验是很困难的!6。
在理论分析的时候、信号⽆论是速度、位移、加速度是没有什差别,只是表现形式不同⽽已。
但对试验⽽⾔就应另当别论了,应考虑试验频段和信号⽅式对测量精度的影响!mjhzhjg的“个⼈认为⾃由模态分析在于了解你设计的结构⾃⾝的⼀些固有特性。
⽽约束模态分析是你这个结构⽤于⼯程时实际的约束边界”概念不对。
对⼯程实际结构的分析模型⼀定是要尽量的符合实际,理论上不同的结构系统(包括材料、结构、边界甚⾄变形程度等)相应的振动固有特性是不⼀样的,没有⽐较的必要,更不会存在⾃由模态特性表⽰固定模态的特征。
不同⼯程中的模型应该都有处理⽅法,也没有⼀定的规则... ...⾄于⼀些结构系统实验或计算很难模拟实际⾃由状态,那么不得不增加的约束也是尽量的对实际状态产⽣较⼩的影响。
当然这也是实际⼯作⽔平所在。
QUOTE:原帖由 xinyuxf 于 2006-9-7 12:00 发表问⼀下系主任,若是模拟飞机振动,那⼈为的加上约束可以吗?⽐如假设模型⼀边固定,然后进⾏模态分析?1,当然可以!2,但⼀般⽽⾔,试验的边界条件是以⼯程实际需要为准的。
万方数据70小型内燃机与摩托车第38卷([K]一∞2[M]){西}={0}(4)求解以上方程就可以确定系统从小到大的几个固有频率值∞i和与之对应的固有模态咖。
(i=1,2,3…,凡)。
在自由振动时,结构中各结点振幅{咖}不全为零,因此式(4)中括号内矩阵的行列式之值必为零,由此得到结构自振频率方程,即:I[K]一∞2[肼]I-0(5)结构刚度矩阵[K]和质量刚度矩阵[M]都是n阶方阵,其中凡是结点自由度的数目,所以式(5)是关于∞2的n次代数方程,由此可求得n个固有频率∞i(i=l,2,3…,n),对于每个固有频率∞。
,由式(4)可确定几个结点振幅构成的一个列向量{咖}i=[咖“,咖乜,…,咖h]1,它们相互之间保持固定的比值,但绝对值可任意变化,它们构成一个向量,称为特征向量,在工程上通常称为结构振型。
到此,通过求解式(5)便可求得系统的固有频率及其对应的振型。
2机体实体模型的建立柴油机机体是一个经铸造、机加工后得到的箱体式结构,其上布有各种加强筋、凸台、轴承孔、水套和油道孔,内有气缸套和各种纵、横隔板,形状较为复杂一J。
建立模型时,在不影响机体计算精度的条件下,对机体结构进行必要的简化,以便提高有限元计算速度。
建立机体的实体模型如图l所示。
图1机体实体模型图3机体有限元模型的建立建立有限元模型包括两部分内容,即有限元模型的建立和单元的划分。
根据有限元原理,单元的选择对有限元的计算精度有很大的影响JJ。
而柴油机机体主要涉及到的实体单元,有四面体单元和六面体单元,由于六面体单元形状规则,难以适应机体结构复杂的外形,四面体恰恰相反,它弥补了六面体的不足,能较好的适应机体复杂的几何外形,经综合考虑选择四面体单元。
考虑到网格的划分密度对四面体单元的计算精度影响比较大,理论上网格越密计算精度越好,为了验证这一理论,采用智能网格划分控制的6级、7级精度来划分网格进行计算,并以此来比较计算结果的差异,网格划分结果如表1、表2、表3所示,机体有限元模型如图2所示。
基于ANSYS Workbench的烟包机推包机构模态分析李杰;曹西京;郑昊【摘要】烟包机是包装行业中重要的包装机器之一,随着们对香烟需求量的增加,香烟生产厂对烟包机的速度要求越来越高.由于振动会造成结构的共振或疲劳,从而破坏结构,所以针对烟包机推包机构高速运动时容易产生振动的问题进行研究,分析推包机构主要部件平面沟槽凸轮,利用Pro/E建立平面沟槽凸轮实体模型,然后导入Workbench软件中进行自由模态分析和约束模态分析,求出其振动特性,为推包机的优化设计提供了必要依据.%Tobacco packing machine is one of the important packaging machines in packing industry. Along with the increase of demand for cigarette,the demand for speed of the machine in cigarette factories is increased.Since the vibration may cause structure resonance or fatigue, the structure may be destroyed,in this case the vibration problem caused by high-speed pushing mechanism of tobacco packing machine is studied,the plane groove cam which is the main part of pushing mechanism is analyzed.W ith Pro/E software the solid model of plane groove cam is built,then it is transmitted into Workbench software,in which free modal analysis and the restraint modal analysis are completed.From the analysis result, the vibration performance is obtained, which provide an essential basis for optimization design of the pushing mechanism.【期刊名称】《机械设计与制造》【年(卷),期】2011(000)008【总页数】3页(P109-111)【关键词】Workbench;烟包机;平面沟槽凸轮;模态分析【作者】李杰;曹西京;郑昊【作者单位】陕西科技大学机电工程学院,西安710021;陕西科技大学机电工程学院,西安710021;陕西科技大学机电工程学院,西安710021【正文语种】中文【中图分类】TH161 引言随着我国国民经济的发展,人们对香烟需求量的增加,香烟生产厂对烟包机的速度要求越来越高。
最近在做结构的模态分析,查找了很多论坛,资料也翻了很多。
有人说这个要做自由模态分析,因为它理论上代表了结构的所有振型才有参考价值,也有人说,模态分析要看具体的边界条件,自由模态中出现的振型不一定会在约束模态中出现,因此要根据实际情况来决定是否用自由模态分析还是约束模态分析。
乍看,两种说法都有道理。
可是想做模态分析来获取有用信息的人糊涂了,因为这两种情况下算的频率值不仅有区别,而且算的值通常差别还很大!
那么到底该听谁的呢?
好了,不绕关子了。
问题就出现在实际与理论的差别上!倾向于做自由模态分析的人偏理论,因为自由模态分析的确可以得到所有结构振型。
而倾向于约束模态分析的人太倾向于实际。
认为约束的就应该按约束的算。
好吧,问题就出在这了,虽然一般来说,约束关系基本是明确的,但是其复杂程度不是我们可以预料到的,由于有限元分析的简化假设,对于约束,尤其是复杂构件的约束我们很难建立其真正的边界条件,那么我们所谓的边界约束也就无从谈起,如贸然采用刚性连接等作为约束,无形中增加了结构的刚度(这也是我们很多人在做约束模态分析时得到的值比自由模态分析时高的原因之一),但是这个刚度增加的来源谁也说不清楚。
所以,我建议的措施是,对于复杂的约束难以确立的构件,倒不如用自由模态分析,起码还能在其中选择我们关心的振型。
可是,如果对复杂件做某些约束下的约束模态分析,我们是无法获知其在其他约束下(有可能正是这个才是真正的约束呢)的振型,那样我们将得不偿失,有时候还会得到错误的结果。
确实是貌似有道理,但要挑出我们需要的那几阶模态谈何容易。
我以前老师的看法就是必须加约束算模态。
做模态分析是为我们分析系统的动力响应提供方便,系统的动力响应是肯定要满足约束条件的。
如果我们做自由模态分析,求出所有模态后,要挑出那些满足约束的模态来是要费很大的劲的。
实际应用中的自由度动辄上万,约束也很复杂。
而且我们曾经从理论上证明过,约束的存在只是去掉了那些不满足约束条件的模态,但其他的模态是没影响的。
具体说就是那些在自由模态中在约束的位置其相对位移是为0的模态约束条件是不会产生作用的,实际就是说加了约束后就是程序自动将那些不满足约束条件的模态去掉了。
至于说约束,我想任何一个分析必需要搞清楚约束和载荷,连约束多没搞清楚,算出自由模态后有什么意义,我们需要做的就是要看结构在特定的环境下满不满足我们的使用要求。
这是任何一个工程师要解决的问题,从广泛的角度讨论结构的基本特性,一般是高校的学者干的事。
至于说到一个约束的准确与否,我想举个很简单的例子,在做精密机床主轴的振动分析时,由于主轴刚度很大,这时候支撑主轴的轴承很重要,甚至起了决定作用,因此做模态时要采用弹性支撑来做,假如说你要是做主轴的自由模态,那是没任何意义的。
约束很复杂时,或者说约束不好也不能太简单化时,逃是逃不过的,很多时候约束的处理水平就是反应你的能力。
回楼上,你的看法是没错。
你举出来的例子也没错,可是有一件事情你忽略了,你说做精密机床主轴振动分析时,对轴承要用柔性件来模拟,这就意味着你对这个约束是非常清晰和明确的。
但是不要忘了,你这个模型中约束只此一处,而且很容易分析出来是何种约束。
但对于很多种情况,如汽车的车身,试问你就那么有信心去找准没一处约束吗?答案应该是否定的吧,所以我们通常见的针对汽车车身的模态试验都是自由模态试验,说的就是这个道理。
数值分析与实验是有区别的。
模态实验选择用自由模态去做,主要原因有两点:1、实验中约束不好加,在计算时就是令位移为零九可以了,但在做实验时,这个约束怎么来加,想要做的话,必须要求支撑的刚度非常之大,固有频率非常之高,否则的话支撑就会严重的影响模型的分析。
这个你可以去理解下,实验中要加个约束肯定是将其与地面相连,这个连
接件是与实验模型连接在一起的,连接件刚度要么很小,那就是自由模态分析,要么很大,否则的话这个连接件会产生很大的影响,因为刚度不够的话就成了一个弹性支撑。
2、加了约束后,自由振动衰减的很快,这对于实验的测量是很不方便的。
要为了保证振动持续时间较长,就必须加激励,这个激励是很复杂的。
所以一般选择做自由模态分析。
实验中,出于实验条件的考虑,很多东西是走了妥协路线的,实验中的有些做法在计算中不是最好的,要仔细去思考实验那样做的原因。
至于约束,我可以明确的说,任何一个东西的约束多是可以找出来的,约束加不准,算出来的结果是没有任何意义的。
我更倾向于自由模态和约束模态都是对实际的模拟,都是对现实情况的分析。
飞机、火箭这些模态分析都是用自由模态的,这些结构也是无约束的结构我们平时做的模态多是约束结构模态,我们做约束模态分析
看了楼主和liu_xiao_jin的讲解,对于自由模态和约束模态有了更为深刻的了解,但还不是很清晰。
我是做船舶轴系的,通常需要计算扭振、纵振、横振,之前我计算就是只留有一个方向的自由度,其他的都约束,求解模态;后来一个朋友说要做自由模态,然后从成百上千个甚至更多的振型找自己需要的(就是与自己需要相同的)。
到目前我还不清楚到底该怎么计算。
自由模态相对于约束模态来讲是简单的做法,不用加约束,模型出来运行一下就能出来结果。
对于应付学位论文来说,这是大部分同学愿意做的。
我看了一些论文,大都做的自由模态分析,影响的我也只做模态分析就想了事。
总的来说,自由模态分析在学校比较常用,约束模态分析在工作中常用,只是个人见解。