有限单元法-上课
- 格式:ppt
- 大小:5.25 MB
- 文档页数:191





地下铁道方向本科生有限单元法授课方式探讨作者:金浩周顺华杨新文来源:《大学教育》 2019年第2期[摘要]针对地下铁道方向本科生有限单元法的教学问题,笔者根据国内外工作学习经历及教学经验,对比同济大学和科罗拉多大学博尔德分校(美国)等高校的教学方式,提出了可供借鉴的授课方式:(1)板书融合多媒体(PPT)教学,经济条件允许下,亦可采用大型触摸屏进行教学;(2)小组模式,包括小组学习、小组讨论及小组复习,充分调动学生学习积极性及利用学生课余时间;(3)现场教学,让学生能切身感受有限单元法模拟的实物,更好地理解有限单元的计算原理。
[关键词]铁道工程;本科生;有限单元法;授课方式1960年,Clough在平面弹性论文中首次采用“有限元法”这一名称。
随着个人计算机及超级计算机处理能力的逐年提高,有限单元法能够解决的问题越来越广、越来越复杂,其已然是工程界使用最为广泛的数值计算方法之一。
如:采用有限单元法对轨道结构进行建模,并耦合车辆多刚体模型,计算车辆运行下轨道的动力加速度等,对轨道减振措施等进行性能评估[1]。
诸如此类复杂工程问题,过去往往采用子结构法配合工程经验,现如今则可以进行基于系统的计算。
因此,有限单元法在地下铁道方向处于越来越重要的地位。
教育的根本目的是为国家培养各行业所需的人才[2]。
因此,有限单元法教学成为工科大学的重要课程之一,但主要以研究生为主。
根据行业需求等综合考虑,同济大学交通运输工程学院城市轨道与铁道工程系在大三设置了有限单元法选修课。
针对地下铁道方向本科生有限单元法授课存在的诸多问题(学生力学基础要求高,授课内容须紧密结合工程等),笔者通过近几年的授课实践,对地下铁道方向本科生有限单元法的授课方式进行了探讨。
一、课程特点(一)前续课程难本科阶段进行有限单元法的授课,与研究生阶段授课不同。
本科阶段在大三学习力学,主要为理论力学、材料力学和结构力学。
在有限单元法内容讲解前,必须安排弹性力学基本知识的讲授。



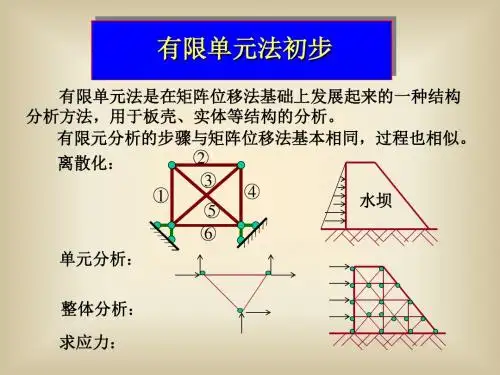
平面问题的有限单元法有限单元法是随着计算机的出现而发展起来的一种有效数值计算方法,有限单元法出现于40年代,被应用于飞机结构分析,有限元这个术语是1956年首先使用的。
目前已广泛地用于工程结构的力学分析中。
第一节基本概念一、实质理想化连续体―――――――单元集合体(解析模拟、逼近求解区域)无限自由度有限个自由度有限单元法首先把结构划分成许多单元,在一定的简化假设前提下,研究单元的力学特性,即单元分析;然后把各单元综合起來, 把局部的力学特性扩展到整体, 即整体分析;12最后导出一组以结构结点位移为未知量的代数方程组。
通过求解方程组而得到单元的结点位移值,就可近似计算出结构任意一点的受力状态。
这种以结点位移为基本未知量的计算方法称为有限单元位移法。
二、理论基础弹性力学:变分原理能量原理基本方程:几何方程、物理方程1. 平面问题的几何方程⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂∂∂∂∂∂∂=⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=v u x y y x x v y u y v x u xy y x 00γεεε3这就是弹性力学平面问题的几何方程,它给出了某一点的位移与该点应变之间的关系。
反映了变形协调关系。
2. 平面问题的物理方程⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧xy y x xy y x E γεεμμμμτσσ2100010112 即: D εζ= 给出了力与变形之间的关系,称为平面问题物理方程,是针对平面应力问题推导出的。
对于平面应变问题,只需将公式中的E 换成21μ-E,把μ换成μμ-1即可。
这样,弹性矩阵D 就变为:4⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----+-=)1(22100011011)21)(1()1(μμμμμμμμE D (2.8)这就是适用于平面应变问题的弹性矩阵。
3. 弹性体的能量原理(1)应变能 在弹性范围内,对于平面问题,某个面积A 的应变能可以用下式表示tdxdy V xy xy y y Ax x )(21γτεσεσ++=⎰⎰ 写成矩阵的形式为5t d x d y V AT ζε⎰⎰=21 (2)外力势能 外力势能用矩阵的形式可表示为∑-=i T i P V P d 式中 {}iy ixi P P =P −−作用在弹性体i 点的外力分量; {}i i i v u =d −−i 点的位移分量(3)弹性体的总势能弹性体在外力作用的总势能定义为应变能和荷载势能之和,即∑⎰⎰-=+=i T i AT PP tdxdy V V E P ζεd 21 (4)最小势能原理6单元的众多的结点位移)(e δ中, 须满足条件:0)(=e P E δ即 0)()(=∂∂e e P E δ的一组位移才是真正的位移。


第二章 杆系结构有限元法由桁架和刚架杆件单元组成的结构在工程中应用非常广泛,在单元不多的情况下用结构力学的处理办法就可以解决,但当单元数增多时就很难计算,而用有限单元法来处理就比较合适,实际上有限单元法最早就是从杆系结构单元发展起来的。
下面我们从最简单的桁架单元开始,了解有限元法的概念和求解步骤。
§2.1 杆单元、平面桁架有限元法平面桁架的每一个单元都是杆单元,它们通过铰链而连接,每个杆只承受由铰节点传来的轴向力。
由于要从单元性质入手,我们取局部坐标系较方便。
在图2.1中杆端编号为i ,终端编号为j ,杆长为l ,x 轴正向指向j 端,建局部坐标系 y x o 。
2.1.1局部坐标系下单元刚度矩阵K对二力杆只有轴向位移才产生应力,我们用位移有限元法。
将位移作为基本未知量,以i u 及j u 分别表示两端的轴向位移,节点位移a 写成列阵形式:[]Tjiuu =a (2.1)与上述位移相应的i ,j 节点对杆件的作用力分别记为:,xi xj F F ,节点力F 写成列阵形式: Txix j F F ⎡⎤=⎣⎦F (2.2)注意:i u ,j u ,xi F ,xj F 沿x 轴正向时为正。
节点位移a 与节点力F 有以下关系:=⋅F K a (2.3)K 称为局部坐标系下单元刚度矩阵,是我们需要求的。
绪言中提到我们要研究未知量在单元内部及在单元节点上值的关系,我们就从这里出发来把K 求出来。
1. 求位移插值函数(又称形函数)单元内位移用 )(x u 表示,它与节点位移i u ,j u 有以下关系:()()()ii jj u x N x u N x u =+=N a (2.4) 形函数矩阵:()()i jN x Nx ⎡⎤=⎣⎦N (2.5)显然形函数必须满足下列条件:x⎩⎨⎧===l x x x N i 001)(⎩⎨⎧===lx x x N j 100)( (2.6)对于二力杆,由于单元应力不变,故位移是线性变化的,则有lx x N i -=1)( lx x N j =)( (2.7)2. 将杆内应变ε与应力σ和节点位移a 联系起来,即本构关系 (应力-应变关系) 应变:()11u x xl l ∂⎡⎤=ε==-=⎢⎥∂⎣⎦a B a ε (2.8) 其中B 为应变几何矩阵。