「精品」高中数学第二章函数2.3函数的应用同步练习新人教B版必修1

高中数学学习材料马鸣风萧萧*整理制作【高中数学新人教B版必修1】2.3《函数的应用》习题【目标要求】１．能把实际问题转化为数学模型．２．能用函数等数学知识解决简单的应用问题．３．培养学生学以致用的思想．【巩固教材--稳扎马步】1．固定电话市话收费规定：前三分钟0.22元（不满三分钟按三分钟计算），以后每分钟0.11元（不满一分钟按一分钟计算），那么某人打市话５５０秒，应该收费（）Ａ．1.10元Ｂ．0.99元Ｃ． 1.21元Ｄ．0.88元2．某汽车运输公司，购买了一批豪华大客车投入客运，据市场分析，每辆客车盈利的总利润ｙ（万元）与营运年数ｘ（ｘ）满足函数关系式ｙ＝，则每辆客车营运多少年可使其营运利润最大（）Ａ．６Ｂ．７Ｃ．６或７Ｄ．７或８3．在一定范围内，某种产品的购买量ｙ吨与单价ｘ元之间满足一次函数关系，如果购买1000吨，每吨为800元；购买2000吨，每吨为700元，一客户购买400吨，单价应该为（）Ａ．820元Ｂ．840元Ｃ．860元Ｄ．880元4．在ｘ克ａ％的盐水中，加入ｙ克ｂ％的的盐水，浓度变成ｃ％，则ｘ与ｙ的函数关系式（）Ａ．Ｂ．Ｃ．Ｄ．【重难突破--重拳出击】5．某厂生产两种成本不同的产品，由于市场销售变化，甲产品按成本提价20％，同时乙产品按成本降价20％，结果都以３0元售出，此时厂家对甲乙两种产品各售出一件，盈亏情况是（）Ａ．不亏不赚Ｂ．赚2.5元Ｃ．赚5.5元Ｄ．亏2.5元6．《中华人民共和国个人所得税法》规定，公民全月工资，薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累积计算：全月应纳税所得额税率不超过500元的部分5％超过500至2000元部分10％超过2000元至5000元部分15％．．．．．．．．．．．．某人一月份应缴纳税款26．78元，则他的当月工资，薪金所得介于（）Ａ．800～900元Ｂ．900～1200元Ｃ．1200～1500元Ｄ．1500～2000元7．某种商品进货单价为40元，若按５０元的价格出售，能卖出50件；若销售单价每上涨１元，则销售量就会减少１件，为了获得最大利润，此商品的最佳售价应定为每件（）Ａ．80元Ｂ．70元Ｃ．60元Ｄ．50元8．当｜ｘ｜１，函数ｙ＝的值有正有负，则实数ａ的取值范围是（）Ａ．Ｂ．ａ－１Ｃ．Ｄ．以上结论都不对9．有一台坏天平，两臂长不相等，其余均精确，现用它称物体的质量，将物体放在左右托盘各称一次，质量分别为ａ，ｂ，则该物体的真实质量是（）Ａ．Ｂ．Ｃ．Ｄ．10．某地用手机打国内长途电话规定：每分钟收市话费0.20元（不满一分钟按一分钟计算），再加上长途费：每６秒收0.07元（不满６秒按６秒计算），如果［ｘ］表示不超过ｘ的最大整数，则用手机打长途的花费ｙ与通话时间ｘ秒之间的函数关系是（）Ａ．ｙ＝［］0.20＋［］0.07Ｂ．ｙ＝［－１］0.20＋［－１］0.07Ｃ．ｙ＝［＋１］0.20＋［＋１］0.07Ｄ．以上都不正确11．某种商品，现在定价为ｐ元，每月卖出ｎ件，根据市场调查显示：定价每上涨ｘ成，卖出的数量就会减少ｙ成，如果涨价后的销售总金额是现在的1.2倍，则用ｘ来表示ｙ的函数关系式为（）Ａ．Ｂ．Ｃ．Ｄ．12．某种产品生产件数ｘ与成本ｙ（万元）之间的函数关系式ｙ＝，若每件产品用料6吨，现有库存原料30吨，明年又可进料900吨，且平均每件成本不能超过25万元，明年最高产量是（）Ａ．150件Ｂ．155件Ｃ．200件Ｄ．1000件【巩固提高--登峰揽月】13．矩形的长为４宽为３，当长增加ｘ，且宽减少时，面积最大，此时ｘ＝，面积为．14．某工厂生产一种产品所需费用Ｐ元，而卖出ｘ吨的价格为每吨Ｑ元，已知Ｐ＝，Ｑ＝，若生产出的产品全部可以卖出，且当产量为150吨时利润最大，此时每吨价格为40元，求实数ａ，ｂ的值．【课外拓展--超越自我】15．某工厂2004年底共有职工1000人，总产值为2000万元，从2005年起10年内该厂总产值每年增加２０万元，职工每年净增ｍ人（ｍ为正整数），设该厂从2005年起第ｘ年（2005年为第一年），该厂人均总产值为ｙ元． （１）写出ｙ与ｘ的函数关系式；（２）要使该厂人均产值年年都有增加，那么每年职工的净增数应该不超过多少人？16．某工厂2005年１月，２月，３月生产某产品分别为１万件，1.2万件，1.3万件，为了估测以后每个月的产量，以这三个月的产量数据为依据，用一个函数模拟产品的月产量ｙ与月份数ｘ的关系，模拟函数可以选择二次函数或函数ｙ＝ （其中ａ，ｂ，ｃ为常数），已知四月份该产品产量为1.37万件，请问用以上哪个函数作为模拟函数较好，并说明理由．答 案 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B DCBDCBCBCCB13．１，22514．因为利润ｙ＝Ｑｘ－Ｐ＝22101100030x ax x bx ----＝1000)(3042--+-x a b x由题意，得⎪⎪⎩⎪⎪⎨⎧=-=-405150308b ab 解之得ａ＝５，ｂ＝４５． 15．（１）由题意的函数关系式为mxxy ++=1000202000（其中≤0ｘ10≤）．（２）根据题意，要使该厂人均产值每年都有增加得，函数ｙ为增函数，设[]10,0,21∈x x ，21x x <，则11221210002020001000202000mx x mx x y y ++-++=-＝)1000)(1000()10)((20001212mx mx m x x ++--，欲使12y y >，只需010>-m ，即10<m ,故要使该厂人均产值年年都有增加，每年职工净增数应不超过９人．16．设)0()(2≠++=p r qx px x f ，则⎪⎩⎪⎨⎧=++=++=++3.1392.1241r q p r q p r q p 即⎪⎩⎪⎨⎧==-=7.035.005.0r q p 所以7.035.005.0)(2++-=x x x f ，所以)4(f ＝1.3，另设)(x g ＝c xbax ++，则 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++3.1332.1221c b a c b a c b a 即⎪⎩⎪⎨⎧=-==25.13.005.0c b a ，所以)(x g ＝25.13.005.0+-x x ，)4(g ＝1.375 由于1.37５－1.37＜1.37－1.3，所以用函数)(x g ＝25.13.005.0+-xx 作为模拟函数较好．。

2.3 函数的应用(Ⅰ)课时过关·能力提升1某债券市场发行三种债券,甲种面值为100元,一年到期本息和为103元;乙种面值为50元,半年到期本息和为51.4元;丙种面值为100元,但买入价为97元,一年到期本息和为100元.作为购买者,分析这三种债券的收益,从小到大排列为()A.乙,甲,丙B.甲,丙,乙C.甲,乙,丙D.丙,甲,乙100元购买债券,如果购买甲种,则一年后为103元;如果购买乙种,则半年后为102.8元,一年后为105.6784元;如果购买丙种,则一年后为100×≈103.1元.2商店某种货物的进价下降了8%,但销售价不变,于是这种货物的销售利润率销售价-进价进价由原来的r%增加到(r+10)%,则r的值等于()A.12B.15C.25D.50a,原进价为x,可以列出方程组:----解这个方程组,消去a,x,可得r=15.3将进货单价为80元的商品按90元一件售出时,能卖出400件,已知该商品每件涨价1元时,其销售量就会减少20件,为了获得最大的利润,其售价应定为()元/件A.110B.105C.100D.95x元,利润为y元,则销售量为(400-20x)件,根据题意,有y=(10+x)(400-20x)=-20x2+200x+4000=-20(x-5)2+4500.故当x=5时,y取得最大值为4500,即当每件涨价5元,也就是售价为95元/件时,可以获得最大利润为4500元.4在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖2小时后的即时价格为3元;g(2)=3表示2小时内的平均价格为3元,下面给出了四个图象,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是(),可知,当即时价格升高时,对应平均价格也升高;反之,当即时价格降低时,对应平均价格也降低,故选项C中的图象可能正确.5一个人以6 m/s的速度去追停在交通灯前的汽车,当他距汽车25 m时,交通灯由红变绿,汽车以1 m/s2的加速度匀加速开走,则()A.人可在7 s内追上汽车B.人可在10 s内追上汽车C.人追不上汽车,两者最近距离为10 mD.人追不上汽车,两者最近距离为7 m,设汽车在C 点开始运动,此时人到达A 点,AC=25m,经t s 后,汽车到达D 点,路程CD= at 2,此时人追到B 点,路程AB=vt ,依题意,汽车与人的距离S=AC+CD-AB=25+ at 2-vt=25+t 2-6t=7+(t-6)2≥ .所以,人不能追上汽车,他与汽车最近的距离是在汽车开动6s 后的瞬间,两者最近距离为7m,故选D .6某工厂生产某种产品的固定成本为200万元,并且生产量每增加一单位产品,成本增加1万元,又知总收入R 是单位产量Q 的函数R (Q )=4Q-Q 2,则总利润L (Q )的最大值是 万元,这时产品的生产数量为 .(总利润=总收入-总成本)(Q )=4Q-Q 2-(200+Q )=-(Q-300)2+250,则当Q=300时,总利润L (Q )取最大值250万元. 3007某批发商批发某种商品的单价P (单位:元/千克)与一次性批发质量x (单位:kg)之间的函数图象如图所示.一零售商仅有现金2 700元,他最多可购买这种商品 kg(不考虑运输费等其他费用).,可得批发这种商品所需费用y (元)与一次性批发质量x (kg)之间的函数关系式为y=从而易得30×50<2700<30×100,故该零售商购买这种商品的质量应在50kg 与100kg 之间,故所购商品的质量最多为=90(kg).8某校校长暑假将带领该校市级三好学生去北京旅游.甲旅行社说:“若校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.(1)设学生数为x人,甲旅行社收费为y甲元,乙旅行社收费为y乙元,分别写出两家旅行社的收费yy乙与学生数x之间的解析式.甲,(2)当学生数是多少时,两家旅行社的收费一样?(3)就学生人数讨论哪家旅行社更优惠?y甲=120x+240(x∈N+),y乙=(x+1)×240×60%=144(x+1)(x∈N+).(2)由120x+240=144x+144,解得x=4,即当学生数为4人时,两家旅行社的收费一样.(3)当x<4时,乙旅行社更优惠;当x>4时,甲旅行社更优惠.9某人定制了一批地砖,每块地砖(如图所示)是边长为1 m的正方形ABCD.点E,F分别在边BC 和CD上,且CE=CF,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元.问点E在什么位置时,每块地砖所需的材料费用最省?W元,CE=x m,则BE=(1-x)m.由于制成△CFE,△ABE和四边形AEFD三种材料的每平方米价格依次为30元、20元、10元, 则W=x2×30+×1×(1-x)×20+---×10=10x2-5x+15=10-.当x=时,W有最小值,即所需材料费用最省.即当点E在距点C m时,每块地砖所需的材料费用最省.10某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)可近似看作一次函数y=kx+b(k≠0)的关系(图象如图所示).(1)根据图象,求一次函数y=kx+b(k≠0)的表达式.(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为s元.①求s关于x的函数表达式;②求该公司可获得的最大毛利润,并求出此时相应的销售单价.由题中图象,可知函数y=kx+b(k≠0)的图象经过点(600,400),(700,300),代入y=kx+b,得解得-故y=-x+ ≤x≤ .(2)①由(1),知s=xy-500y=(-x+1000)(x-500)=-x2+1500x- ≤x≤ .②由①可知,s=-(x-750)2+62500,此函数图象开口向下,对称轴为x=750.故当x=750时,s max=62500.即该公司可获得的最大毛利润为62500元,此时相应的销售单价为750元/件.★11某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图所示).(1)分别写出两种产品的收益与投资额的函数关系;(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?设投资债券等稳健型产品的收益与投资额的函数关系式为f(x)=k1x(k1≠0),投资股票等风险型产品的收益与投资额的函数关系式为g(x)=k2(k2≠0),则依题意知f(1)==k1,g(1)==k2,故f(x)=x(x≥ g(x)=(x≥ .(2)设投资债券等稳健型产品x万元,则投资股票等风险型产品为(20-x)万元.依题意,得y=f(x)+g(20-x)=x+- ≤x≤ .令-=t,则 ≤t≤ ,且x=20-t2,即y=-t=-(t-2)2+ ≤t≤ ).故当t=2,即x=20-22=16时,收益最大,且最大收益为3万元.因此,当投资债券类产品16万元,投资股票类产品4万元时,总收益最大,最大收益为3万元.。

2．1.1 函数1．下列说法中，不正确的是( )A ．函数值域中每一个数都有定义域中的一个数与之对应B ．函数的定义域和值域一定是无限集C ．定义域和对应关系确定后，函数的值域也就确定了D ．若函数的定义域中只有一个元素，则值域中也只有一个元素2．下列说法中，正确的个数是( )①定义域不同，两个函数就不同 ②对应法则不同，两个函数就不同 ③定义域和值域都分别相同的函数，一定是同一函数A ．1B ．2C ．3D ．03．下列集合A 到集合B 的对应法则f 是映射的是( )A ．A ＝{－2,0,2}，B ＝{－4,0,4}，f ：A 中数的平方B ．A ＝{0,1}，B ＝{－1,0,1}，f ：A 中数的平方根C ．A ＝Z ，B ＝Q ，f ：A 中数的倒数D ．A ＝R ，B ＝{x|x>0}，f ：A 中数的平方4．函数y ＝2x ＋3－12－x ＋1x的定义域为__________． 5．把下列集合用区间表达出来：(1){x|x≠2，且x≠1}； (2){x|13≤x≤12}； (3){x|x≥3或x≤－3}；(4){x|－2≤x≤2，且x≠1}．1．下列四组函数中，表示同一函数的是( )A ．f(x)＝x ，g(x)＝(x)2B ．f(x)＝x ，g(x)＝x 2C ．f(x)＝x ＋2，g(x)＝x 2－4x －2D ．f(x)＝x ，g(x)＝3x 32．下列四个命题正确的有( )①函数是定义域到值域的对应关系 ②f(x)＝x －4＋1－x 是函数 ③f(x)＝5，因这个函数的值不随x 的变化而变化，所以f(t 2＋1)＝5④y＝2x(x∈N )的图象是一条直线A ．1个B ．2个C ．3个D ．4个3．下列对应是集合A 到集合B 的一一映射的是…( )A ．A ＝B ＝R ，f ：x→y＝1x，x∈A，y∈B B ．A ＝B ＝R ，f ：x→y＝x 2，x∈A，y∈BC ．A ＝B ＝R ，f ：x→y＝1x ＋|x|，x∈A，y∈B D ．A ＝B ＝R ，f ：x→y＝x 3，x∈A，y∈B4．已知f(x)＝x 2＋ax ＋b ，满足f(1)＝f(2)＝0，则f(－1)＝__________.5．已知f(x)＝x 2＋1，则f(3x ＋2)＝__________.6．已知f(x)＝11＋x(x∈R ，且x≠－1)，g(x)＝x 2＋2. (1)求f(2)、g(2)的值；(2)求f[g(2)]的值；(3)求f[g(x)]的解析式．7．求下列函数的值域：(1)y ＝x －1(x≥4)；(2)y ＝2x ＋1，x∈{1,2,3,4,5}．1．设M ＝{x|0≤x≤2}，N ＝{y|0≤y≤2}，给出下列四个图形，其中能表示从集合M 到集合N 的函数关系的有( )A ．0个B ．1个C ．2个D ．3个2．以下各图表示的对应构成映射的个数是( )A ．3B ．4C ．5D ．63．若函数y ＝f(x)的定义域是[－2,4]，则函数g(x)＝f(x)＋f(－x)的定义域是( )A ．[－4,4]B ．[－2,2]C ．[－4，－2]D ．[2,4]4．定义域为R 的函数y ＝f(x)的值域为[a ，b]，则函数y ＝f(x ＋a)的值域为( )A ．[2a ，a ＋b]B ．[0，b －a]C ．[a ，b]D ．[－a ，a ＋b]5．若f(x ＋1)的定义域为[0,3]，则f(x)的定义域为__________．6．已知A ＝B ＝R ，x∈A，y∈B，f ：x→y＝ax ＋b 是从A 到B 的映射，若1和8的原象分别为3和10，则5在f 作用下的象为__________．7．已知集合M ＝{a ，b ，c}，N ＝{1,2,3,4}，则从M 到N 的映射有__________个，从N 到M 的映射有__________个．8．已知函数f(x)＝x ax ＋b(a ，b 为常数，且a≠0)满足f(2)＝1，且f(x)＝x 有唯一解，求y ＝f(x)和f[f(－3)]的值．9．若f ：y ＝3x ＋1是从集合A ＝{1,2,3，k}到集合B ＝{4,7，a 4，a 2＋3a}的一个映射，求自然数a ，k 及集合A 、B.10．求下列函数的解析式．(1)已知f(1＋1x )＝x 1－x 2，求f(x)； (2)已知f(x ＋4)＝x ＋8x ，求f(x)．答案与解析课前预习1．B 函数的定义域和值域只要是非空数集即可．2．B ①和②正确，两函数相同必须满足定义域和对应法则相同，但定义域与值域都分别相同的函数，对应法则不一定相同．3．A 集合A 中每个元素的平方均有值在集合B 中；B 中1的平方根是±1，即1有两个象；C 中0没有象；D 中0的平方是0，但0∉{x|x>0}．点评：判断一个对应是否是映射，先看第一集合A ：看A 中元素是否都有对应元素，若有再看对应元素是否唯一；至于B 中元素无任何要求．4．{x|－32≤x<2，且x≠0} 要使函数有意义，必须⎩⎪⎨⎪⎧ 2x ＋3≥0，2－x>0，x≠0，∴－32≤x<2，且x≠0. 5．解：(1)(－∞，1)∪(1,2)∪(2，＋∞)；(2)[13，12]； (3)(－∞，－3]∪[3，＋∞)；(4)[－2,1)∪(1,2]．课堂巩固1．D A 中f(x)＝x 的定义域为R ，g(x)的定义域为{x|x≥0}，两函数的定义域不同；B中g(x)＝x 2＝|x|，它与f(x)＝x 的对应法则不同；C 中g(x)＝x 2－4x －2的定义域为{x|x≠2}，它与f(x)＝x ＋2的定义域不同；D 中g(x)＝3x 3＝x ，它与f(x)＝x 的定义域和对应法则相同，所以是同一函数．2．B 由函数定义可知①正确；②中函数的定义域为∅，所以不是函数；③中的函数值不随自变量的变化而变化，所以正确；④中的图象应是离散的点．3．D A 中，集合A 中的元素0在f 下，B 中没有元素和它对应，这个对应不是映射；B 中集合A 中的元素±1在f 下的象都是1，故排除B ；C 中集合B 中的负数和零没有原象和它对应，故排除C ；D 符合一一映射的定义．4．6 ∵f(1)＝f(2)＝0，∴⎩⎪⎨⎪⎧ 1＋a ＋b ＝0，4＋2a ＋b ＝0.解得⎩⎪⎨⎪⎧ a ＝－3，b ＝2. ∴f(x)＝x 2－3x ＋2.∴f(－1)＝(－1)2－3×(－1)＋2＝6.5．9x 2＋12x ＋5 f(3x ＋2)＝(3x ＋2)2＋1＝9x 2＋12x ＋5.6．解：(1)f(2)＝11＋2＝13，g(2)＝22＋2＝6. (2)f[g(2)]＝f(6)＝11＋6＝17. (3)f[g(x)]＝f(x 2＋2)＝11＋(x 2＋2)＝1x 2＋3. 点评：解题时要理解对应法则“f”和“g”的含义，在求f[g(x)]时，应遵循“先内后外”的原则．7．解：(1)∵x≥4，∴x ≥2. ∴x －1≥1.∴y≥1，即函数的值域为[1，＋∞)．(2)x ＝1时，y ＝3；x ＝2时，y ＝5；x ＝3时，y ＝7；x ＝4时，y ＝9；x ＝5时，y ＝11. ∴y∈{3,5,7,9,11}．课后检测1．B 由函数的定义判断可得只有②表示的是从集合M 到集合N 的函数关系．因为①中的函数定义域不是M ；③中的函数值域为[0,3]，不是N ；而④中的图象不能表示函数关系．2．A (1)(2)(3)这三个图所表示的对应都符合映射的定义；对于(4)(5)，左边的每一个元素在右边有2个元素与之对应，所以不是映射；对于(6)，左边的元素a 3、a 4在右边没有元素与之对应，所以不是A 到B 的映射．点评：所谓映射，是指一对一、多对一的对应，且A 中元素无剩余，以此判断既准确又迅速．3．B 由⎩⎪⎨⎪⎧ －2≤x≤4，－2≤－x≤4，得⎩⎪⎨⎪⎧ －2≤x≤4，－4≤x≤2. ∴－2≤x≤2.4．C f(x)的值域为[a ，b]，则y ＝f(x ＋a)是将y ＝f(x)左右平移，因而不改变值域．5．[1,2] ∵f(x ＋1)的定义域为[0,3]，∴0≤x≤3，则1≤x ＋1≤2.故f(x)的定义域为[1,2]．点评：已知f[φ(x)]的定义域，求f(x)的定义域的解题方法是：若f[φ(x)]的定义域为D ，则φ(x)在D 上的取值范围即为f(x)的定义域．6．3 由题意⎩⎪⎨⎪⎧ 3a ＋b ＝1，10a ＋b ＝8，解得⎩⎪⎨⎪⎧a ＝1，b ＝－2， ∴f：x→y＝x －2.∴5在f 作用下的象为5－2＝3.7．64 81 映射是有顺序的，从A 到B 的映射与从B 到A 的映射是不一样的．若A 中有m 个元素，B 中有n 个元素，则A→B 共有n m 个不同映射，从B→A 有m n 个不同映射．8．解：∵f(2)＝1，∴22a ＋b＝1. ∴2a＋b ＝2.①又∵f(x)＝x 有唯一解，即x ax ＋b＝x 有唯一解， ∴x·1－ax －b ax ＋b ＝0，得x 1＝0，x 2＝1－b a. ∵有唯一解，∴x 1＝x 2＝0，得b ＝1. 由①知a ＝12. ∴f(x)＝x 12x ＋1＝2x x ＋2. ∴f(－3)＝－6－3＋2＝6. ∴f[f(－3)]＝f(6)＝2×66＋2＝32. 9．解：∵1的象是4,7的原象是2，∴可判断A 中元素3的象要么是a 4，要么是a 2＋3a.由a 4＝10且a∈N ，知不存在a.∴a 2＋3a ＝10，即a 1＝－5(舍去)，a 2＝2.又集合A 中元素k 的象只能是a 4＝16，∴3k＋1＝16.∴k＝5.∴A＝{1,2,3,5}，B ＝{4,7,16,10}．10．解：(1)令1＋1x ＝t(t≠1)，则x ＝1t －1. 又f(1＋1x )＝x 1－x 2， ∴f(t)＝1t －11－(1t －1)2＝t －1(t －1)2－1＝t －1t 2－2t . ∴f(x)＝x －1x 2－2x(x≠1且x≠2)． (2)∵f(x ＋4)＝x ＋8x ＝(x ＋4)2－16，令t ＝x ＋4≥4，∴f(t)＝t 2－16(t≥4)．∴f(x)＝x 2－16(x≥4)．点评：换元法求f(x)是常用的方法，但要特别注意确定中间变量t 的取值范围，否则不能正确确定f(x)的定义域．。

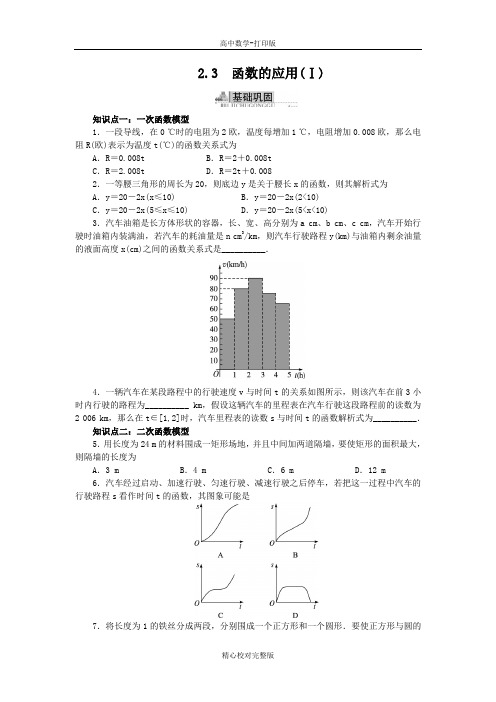
2.3 函数的应用(Ⅰ)知识点一：一次函数模型1．一段导线，在0 ℃时的电阻为2欧，温度每增加1 ℃，电阻增加0.008欧，那么电阻R(欧)表示为温度t(℃)的函数关系式为A．R＝0.008t B．R＝2＋0.008tC．R＝2.008t D．R＝2t＋0.0082．一等腰三角形的周长为20，则底边y是关于腰长x的函数，则其解析式为A．y＝20－2x(x≤10) B．y＝20－2x(2<10)C．y＝20－2x(5≤x≤10) D．y＝20－2x(5<x<10)3．汽车油箱是长方体形状的容器，长、宽、高分别为a cm、b cm、c cm，汽车开始行驶时油箱内装满油，若汽车的耗油量是n cm3/km，则汽车行驶路程y(km)与油箱内剩余油量的液面高度x(cm)之间的函数关系式是__________．4．一辆汽车在某段路程中的行驶速度v与时间t的关系如图所示，则该汽车在前3小时内行驶的路程为__________ km，假设这辆汽车的里程表在汽车行驶这段路程前的读数为2 006 km，那么在t∈[1,2]时，汽车里程表的读数s与时间t的函数解析式为__________．知识点二：二次函数模型5．用长度为24 m的材料围成一矩形场地，并且中间加两道隔墙，要使矩形的面积最大，则隔墙的长度为A．3 m B．4 m C．6 m D．12 m6．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s看作时间t的函数，其图象可能是7．将长度为1的铁丝分成两段，分别围成一个正方形和一个圆形．要使正方形与圆的面积之和最小，正方形的周长应为__________．8．将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售量就减少20个，为了赚得最大利润，售价应为__________元．9．如图所示，用长为l 的铁丝弯成下部分为矩形，上部分为半圆形的框架，若矩形的一边长为2x ，求此框架围成的封闭图形的面积y 与x 的函数关系．能力点一：运用函数模型解决应用问题10．在x 克a%的盐水中，加入y 克b%的盐水，浓度变为c%，则x 与y 的函数关系式为A ．y ＝c －a c －b xB ．y ＝c －a b －c xC ．y ＝a －c b －c xD ．y ＝b －c c －ax11．为了稳定市场，确保农民增收，某农产品的市场收购价格a 与其前三个月的市场收购价格有关，且使a 与其前三个月的市场收购价格之差的平方和最小．若下表列出的是该产品前6则7月份该产品的市场收购价格应为A ．69元B ．70元C ．71元D ．72元 12．在国内投寄平信，每封不超过20克重应付邮资80分，超过20克但不超过40克重付邮资160分，将每封信应付邮资(分)表示为信重(0<x≤40克)的函数，其表达式为__________．13．某校高一(8)班共有学生50人，据统计原来每人每年用于购买饮料的平均支出是a 元．经测算和市场调查，若该班学生集体改饮某品牌的桶装纯净水，则年总费用由两部分组成，一部分是购买纯净水的费用，另一部分是其他费用780元，其中纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图所示的关系．(1)求x 与y 的函数关系．(2)若该班每年需要纯净水380桶，且a 为120时，请你根据提供的信息分析一下：该班学生集体改饮桶装纯净水与个人买饮料相比，哪一种花钱更少？能力点二：建立函数模型解决应用问题14．一根蜡烛长20 cm，点燃后每小时燃烧5 cm，燃烧时每小时剩下的h(cm)与燃烧时间t(h)的函数关系用图象表示应为15．物体从高处静止状态下落，下落的路程与开始下落所经过的时间的平方成正比，已知开始下落的最初两秒钟，物体下落了19.6 m，如果下落时间为 5 s，则下落距离是__________m.16．有l m长的钢材，要做成如图所示的窗架，上半部分为半圆，下半部分为六个全等矩形组成的矩形．试问小矩形的长、宽之比为多少时，窗所通过的光线最多，并具体算出窗框面积的最大值．17．为了更好地了解鲸的生活习性，某动物保护组织在受伤的鲸身上安装了电子监测装置，从海岸放归点A处(如图所示)把它放归大海，并沿海岸线由西到东不停地对鲸进行了长达40分钟的跟踪观测，每隔10分钟采点测量数据如下表(设鲸沿海面游动)，然后又在观测站B 处对鲸进行生活习性的详细观测．已知AB ＝15 km ，观测站B 的观测半径为5 km.(1)据表中信息：①计算出鲸沿海岸线方向运动的速度，②试写出a 、b 近似满足的关系观测时间t(分钟)跟踪观测点到放归点的距离a(km)鲸位于跟踪观测点正北方向的距离b(km)10 1 0.999 20 2 1.413 30 3 1.732 4042.001(2)若鲸继续以(1)②中运行路线运动，试预测，该鲸经过多长时间(从放归时开始计时)，可进入前方观测站B 的观测范围？并求出可持续观测的时间．(注：41≈6.40，精确到1分钟)答案与解析基础巩固1．B2．D 由题意，y ＝20－2x 且满足y>0，x>y2，∴5<x<10.3．y ＝abn(c －x)(0≤x≤c)4．220 s ＝1 976＋80t(1≤t≤2) 该汽车在前3个小时内行驶的路程为50×1＋80×1＋90×1＝220(km)．由于这辆汽车在行驶这段路程前的里程表读数为2 006 km ，∴当t∈[1,2]时，汽车里程表读数s ＝2 006＋50×1＋80(t －1)＝1 976＋80t(1≤t≤2)．5．A 设隔墙长x m ，矩形面积为S m 2，则S ＝x·24－4x 2＝x(12－2x)＝－2(x －3)2＋18，∴x＝3时，S 有最大值18.6．A 方法一：根据加速行驶s ＝12at 2，匀速行驶s ＝vt ，减速行驶s ＝vt －12at 2结合函数图象选A.方法二：根据图象进行分析，汽车启动、加速时，路程增加得越来越快；匀速行驶时，路程均匀增加；减速时，路程增加得越来越慢，直到停止时，路程不变．7.44＋π 设正方形周长为x ，则边长为x 4，圆周长为(1－x)，圆的半径为1－x 2π(0<x<1)．依题意得，面积之和为x 216＋π(1－x 2π)2＝4＋πx 2－8x ＋416π.当x ＝12·84＋π＝44＋π时，有最小值．即正方形的周长为44＋π.8．95 设涨价x 元，则利润y ＝(90＋x)(400－20x)－80(400－20x)＝(10＋x)(400－20x)＝－20x 2＋200x ＋4 000＝－20(x －5)2＋4 500，∴当x ＝5时，y 最大．∴当售价为90＋5＝95(元)时，利润最大． 9．解：由题意，得y ＝x 2π2＋l －2x －xπ2×2x＝π2x 2＋lx －2x 2－πx 2＝－(2＋π2)x 2＋lx.∵l －2x －xπ2>0， ∴0<x<l 2＋π. ∴y＝－(2＋π2)x 2＋lx ，x∈(0，l2＋π)．能力提升10．B11．C f(a)＝(a －71)2＋(a －72)2＋(a －70)2＝3(a －71)2＋2，当a ＝71时，f(a)最小．12．f(x)＝⎩⎪⎨⎪⎧80，0<x≤20160，20<x≤4013．解：(1)由题意，可设y 与x 的函数关系为y ＝kx ＋b(k≠0)，把(4,400)，(5,320)代入得⎩⎪⎨⎪⎧400＝4k ＋b ，320＝5k ＋b ，解得⎩⎪⎨⎪⎧k ＝－80，b ＝720.所以y ＝－80x ＋720.(2)当a ＝120时，若购买饮料，则总费用为120×50＝6 000(元)；若集体改饮桶装纯净水，设所有的费用为w 元，由380＝－80x ＋720，得x ＝4.25.∴w＝380×4.25＋780＝2 395(元)<6 000(元)． ∴该班学生集体改饮桶装纯净水更省钱． 14．B15．122.5 设路程y 与时间t 满足y ＝kt 2，则19.6＝k×4， ∴k＝4.9.∴y＝4.9t 2.当t ＝5时，y ＝4.9×52＝122.5.16．解：设小矩形长为x ，宽为y ，窗框面积为S ，则由图形条件，可得11x ＋πx＋9y ＝l ，∴9y＝l －(11＋π)x，S ＝πx 22＋6xy ＝π2x 2＋23[lx －(11＋π)x 2]＝－44＋π6(x －2l 44＋π)2＋2l2344＋π.要使窗所通过的光线最多，即要窗框面积最大，∴当x ＝2l 44＋π，y ＝l －11＋πx9＝22－πl944＋π，即x y ＝1822－π≈1∶1时，窗框面积S 有最大值S max ＝2l2344＋π.拓展探究17．解：(1)①由表中所给信息可知，鲸沿海岸线方向每隔10分钟前进一公里．因此鲸沿海岸线方向运动速度为1÷16＝6(km/h)．②由表中所给信息可知a 、b 近似地满足：b ＝a ，用描点法可作出其图象如图所示．(2)设鲸运动路线的点P 处处在观测站B 的观测范围，并设P 点坐标为(a ，b)．过P 作AB 的垂线，垂足为Q ，则BQ ＝|15－a|，PQ ＝b ，而(PB)2＝PQ 2＋BQ 2，即(PB)2＝b 2＋(15－a)2， 而PB≤5. ∴b 2＋(15－a)2≤25.又b 2＝a ，∴a 2－29a ＋200≤0，解得11.3≤a ≤17.7.故鲸经过113分钟进入观测站B 的观测范围，持续观测64分钟.。

第二章 2.3 函数的应用（Ⅰ）一、选择题1．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后为了赶时间加快速度行驶，与以上事件吻合得最好的图象是( )[答案] C[解析] 选项A ，随时间的推移，小明离学校越远，不正确；选项B ，先匀速，再停止，后匀速，不正确；选项C ，与题意想吻合；选项D ，中间没有停止，故选C ．2．某地固定电话市话收费规定：前三分钟0.20元(不满三分钟按三分钟计算)，以后每加一分钟增收0.10元(不满一分钟按一分钟计算)，那么某人打市话550 s ，应支付电话费( )A ．1.00元B ．0.90元C ．1.20元D ．0.80元[答案] B[解析] y ＝0.2＋0.1×([x ]－3)([x ]是不小于x 的最小整数，x >0)，令x ＝55060，故[x ]＝10，则y ＝0.9.3．某厂有许多形状为直角梯形的铁皮边角料，为了降低消耗，现要从这些边角料上截取矩形铁片(如图所示)．当截取的矩形面积最大时，矩形两边的长x ，y 应为( )A ．x ＝15，y ＝12B ．x ＝12，y ＝15C ．x ＝14，y ＝10D ．x ＝10，y ＝14[答案] A[解析] 本题考查二次函数的应用．结合图形，可得x 20＝24－y 16，得y ＝24－4x5，矩形面积S ＝xy ＝x (24－4x 5)＝－4x 25＋24x ，所以当x ＝－242×－45＝15时，S 最大，此时y ＝24－45×15＝12，故选A ． 4．某公司招聘员工，面试人数按拟录用人数分段计算，计算公式为 y ＝⎩⎪⎨⎪⎧4x 1≤x <10，x ∈N ＋2x ＋10 10≤x <100，x ∈N ＋1.5xx ≥100，x ∈N ＋，其中，x 代表拟录用人数，y 代表面试人数．若应聘的面试人数为60，则该公司拟录用人数为( )A ．15B ．40C ．25D ．130[答案] C[解析] 令y ＝60，若4x ＝60，则x ＝15>10，不合题意； 若2x ＋10＝60，则x ＝25，满足题意； 若1.5x ＝60，则x ＝40<100，不合题意． 故拟录用人数为25人． 二、填空题5．图中折线是某电信局规定打长途电话所需要付的电话费y (元)与通话时间t (min)之间的函数关系图象，根据图象填空：通话2 min ，需付电话费____元；通话5 min ，需付电话费____元；如果t ≥3 min，电话费y (元)与通话时间t (min)之间的函数关系式是________________．[答案] 3.6 6 y ＝1.2t (t ≥3)[解析] 由图知，通话2分钟，需付电话费3.6元； 通话5分钟需付电话费6元；当t ≥3时，设y ＝kx ＋b ，则有⎩⎪⎨⎪⎧3.6＝3k ＋b 6＝5k ＋b ，解得k ＝1.2，b ＝0，∴y ＝1.2t (t ≥3)．6．甲同学家到乙同学家的途中有一公园，甲到公园的距离与乙到公园的距离都是2 km.如图表示甲从家出发到乙同学家经过的路程y (km)与时间x (min)的关系，其中甲在公园休息的时间是10 min ，那么y ＝f (x )的表达式为______________．[答案] y ＝⎩⎪⎨⎪⎧115x 0≤x ≤30230<x <40110x －240≤x ≤60[解析] 由图象知是一个分段函数，且各段均是直线，可用待定系数法求得．三、解答题7．商店出售茶壶与茶杯，茶壶每个定价20元，茶杯每个5元，该商店推出两种优惠办法：①买一个茶壶送一个茶杯，②按购买总价的92%付款．某顾客购买茶壶4个，茶杯若干个(不少于4个)，若购买茶杯数x 个，付款为y (元)，试分别建立两种优惠办法中，y 与x 的函数关系式，并指出如果该顾客需要购买茶杯40个，应选择哪种优惠办法？[解析] 由优惠办法①得函数关系式为y 1＝20×4＋5(x －4)＝5x ＋60(x ≥4，x ∈N *)． 由优惠办法②得函数关系式为y 2＝(20×4＋5x )×92%＝4.6x ＋73.6(x ≥4，x ∈N *)． 当该顾客购买茶杯40个时，采用优惠办法①应付款y 1＝5×40＋60＝260元；采用优惠办法②应付款y 2＝4.6×40＋73.6＝257.6元，由于y 2<y 1，因此应选择优惠办法②.一、选择题1．随着海拔高度的升高，大气压强下降，空气中的含氧量也随之下降，且含氧量y (g/m 3)与大气压强x (kPa)成正比例函数关系．当x ＝36 kPa 时，y ＝108 g/m 3，则y 与x 的函数关系式为( )A ．y ＝3x (x ≥0)B ．y ＝3xC ．y ＝13x (x ≥0)D ．y ＝13x[答案] A[解析] 由题意设y＝kx(k≠0)，将(36,108)代入解析式可得k＝3，故y＝3x，考虑到含氧量不可能为负，可知x≥0.2．某商场以每件30元的价格购进一种商品，试销售中发现，这种商品每天的销量m(件)与每件的售价x(元)满足一次函数：m＝162－3x.若要每天获得最大的销售利润，每件商品的售价应定为( )A．30元B．42元C．54元D．越高越好[答案] B[解析] 设日销售利润为y元，则y＝(x－30)(162－3x)，30≤x≤54，将上式配方后得y＝－3(x－42)2＋432，当x＝42时，y取得最大值．故每件商品的售价定为42元时，每天才能获得最大的销售利润．3．某公司在甲、乙两座仓库分别有农用车12辆和6辆．现需要调往A县10辆，B县8辆，已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元；从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元．则总费用最少为( ) A．300元B．400元C．700元D．860元[答案] D[解析] 设从甲仓库调到A县的车辆数为x，则从甲仓库调往B县的车辆数为12－x，从乙仓库调往A县的车辆数为10－x，从乙仓库调往B县的车辆数为6－(10－x)＝x－4.设总的费用为y，则y＝40x＋80×(12－x)＋30×(10－x)＋50×(x－4)＝1 060－20x(4≤x≤10，x∈N)要想使运费y最少，则需x最大，所以当x＝10时，运费y最少为860元．4．(2019～2019学年度广东珠海四中高一上学期月考)如图，液体从一个圆锥形漏斗漏入一圆柱形桶中，开始时漏斗中盛满液体，经过3秒漏完，圆柱形桶中液面上升速度是一个常量，则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是图中的( )[答案] B[解析] 单位时间内圆柱形桶中液体增加的体积相等，而漏斗容积上大下小，故液面下降先慢后快，故选B ．二、填空题5．某商人将彩电先按原价提高40%，然后在广告中写上“大酬宾，八折优惠”，结果是每台彩电比原价赚了270元，那么每台彩电原价是________元．[答案] 2 250[解析] 设每台彩电原价x 元，依题意得80%·x (1＋40%)－x ＝270，解得x ＝2 250.6．某厂原来月产量为a ，一月份增产10%，二月份比一月份减产10%，设二月份产量为b ，则a 与b 的大小关系是________________．[答案] a >b[解析] 本题考查函数的应用．因为b ＝a (1＋10%)·(1－10%)＝a [1－(10%)2]＝a (1－1100)，即b ＝a ×99100.故a >b . 三、解答题7．某人定制了一批地砖，每块地砖(如图所示)是边长为1 m 的正方形ABCD ，点E 、F 分别在边BC 和CD 上，且CE ＝CF ，△CFE 、△ABE 和四边形AEFD 均由单一材料制成，制成△CFE 、△ABE 和四边形AEFD 的三种材料的每平方米价格依次为30元、20元、10元．问点E 在什么位置时，每块地砖所需的材料费用最省？ [解析] 设CE ＝x m ，则BE ＝(1－x ) m ，每块地砖的费用为W ，且制成△CFE 、△ABE 和四边形AEFD 三种材料的每平方米价格依次为30元、20元、10元．则W ＝12x 2·30＋12×1×(1－x )×20＋[1－12x 2－12×1×(1－x )]×10＝10x 2－5x ＋15＝10(x －14)2＋1158.当x ＝14＝0.25 m 时，W 有最小值，即费用最省．答：当点E 在距点C 为0.25 m 时，每块地砖所需费用最省．8．有甲、乙两种商品，经营销售这两种商品所能获得的利润依次为Q 1万元和Q 2万元，它们与投入资金x 的关系是Q 1＝15x ，Q 2＝35x .今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入应分别为多少？[解析] 设投入甲x 万元，则投入乙(3－x )万元， 利润Q 1＋Q 2＝15x ＋353－x ，令3－x ＝t (0≤t ≤3)，则x ＝3－t 2， ∴Q ＝15(3－t 2)＋35t ＝－15t 2＋35t ＋35＝－15(t －32)2＋2120，∴当t ＝32，即x ＝34时，Q 取得最大值2120，此时，3－x ＝94.∴为获得最大利润，对甲、乙两种商品的资金投入应分别为34万元和94万元．。

第二章函数（必修1人教B版）A ．y ＝B ．y ＝-3x 2＋1C ．y ＝2xD ．y ＝|x |A ．(，1)B ．(1，)C ．(，1]D ．[1，)-∞+∞-∞+∞ 9. 关于 的一元二次方程的两个实数根分别是 , ,且=7，则的值是( )A.1B.12C.13D.25 10.已知＝()y f x 是定义在R 上的奇函数，则下列函数中为奇函数的是( )①()＝y f |x|；②＝(－)y f x ；③＝()y xf x ； ④y ＝f (x )＋x . A ．①③ B ．②③ C ．①④D ．②④A.12-B.14- C ．14 D ．1212.已知定义在R 上的奇函数f (x ) 满足 － ＝－ ，且在区间 上是增函数，则( )A ．()()0－25＜11＜8f ()f fB ．()()08＜11＜(－25)f f fC ．()()011＜8＜(－25)f f fD ．()()0(－25)＜8＜11f f f二、填空题(本大题共4小题，每小题4分，共 16分)13.已知函数 f (x )＝3－axa －1(a ≠1)．(1)若 ，则 的定义域是________； (2)若f (x )在区间(0,1]上是减函数，则实数a 的取值范围是 .14.已知函数则.15．已知 ＋ ＝ － 且 ＝4，则 的值为__ ____． 16. 已知方程 －4| |＋5＝ 有四个全不相等的实根，则实数 的取值范围是___ _． 三、解答题（本大题共6小题，共74分） 17．（12分）求下列函数的定义域：（1）xx x y -+=||)1(0；（2）xxx y 12132+--+=．18.（12分）作出下列各函数的图象：(1) ＝ － ， ∈Z ；(2＝－0)．19.（12分）已知函数对于任意x，y∈R，总有＋＝＋，且当时，，＝－错误！未定义书签。

.(1)求证：在R上是减函数；(2)求在－上的最大值和最小值．20.(12分)设是定义在R上的奇函数，且对任意实数，恒有＋＝－．当时，＝－.(1) 求证：是周期函数；(2) 当时，求的解析式；(3) 计算＋＋＋＋．21.（12分）已知函数＝是奇函数．(1)求实数m 的值；(2)若函数 在区间 － ， － 上单调递增，求实数a 的取值范围．22.（14分）已知22444（）f x x ax a a =-+--在区间[0，1]内有最大值-5，求a 的值及函数表达式（）f x ．第二章 函 数（必修1人教B 版）一、选择题二、填空题13． 14． 15. 16. 三、计算题 18.19.20.21.22.第二章 函 数 （必修1人教B 版）1. D 解析：由列表法表示的函数直接观察可得.2. D 解析: A 选项中的任意一个角总对应唯一的一个正弦值； B 选项中任意一个正方形的边长总对应唯一的一个面积；C 选项中任意的正n 边形边数（n ≥3）总对应唯一的顶点角度之和0(2）18n -∙︒； 故A ，B ，C 选项均为函数关系，而D 选项中的任意一个年龄对应的身高不唯一，故不是函数关系，故选D . 3.C 解析：因为函数()f x 的定义域为R ,所以 的取值范围也是 , 因此函数 ()()f x a f t +=的值域与函数()f x 的值域相同，都是 .4. A 解析：因为12220(－)(－)x x <，若12x x <，则有122x x <<，即2124－x x <<.又当2x >时，()f x 单调递增且(－)＝－(＋4)f x f x ，所以有()()211(4－)＝－f x f x f x <，即()()012＋f x f x <；若21x x <，同理()()012＋f x f x <，故选A.6.C 解析：距学校距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，后段直线段比前段下降的快，故C 图象吻合的最好. 7.D 解析：由函数单调性定义知选D.8. B 解析：由根式内部的代数式大于等于0求出集合M ，然后直接利用补集概念求解． 由01x -≥，得1x ≤，即（，1]M =-∞.又全集为R ，所以（1，）M =+∞ðR ．故选B . 9. C 解析：∵ 方程有两个实数根，∴ Δ ≥0, ∴ 或 .根据根与系数的关系得 .又 ＝ ，即 ＝ ，代入得到 - ,即 - , 解得 , (不合题意，舍去). 则关于 的一元二次方程为 , 根据根与系数的关系得 , ,所以 ＝＝ -4×（ ）＝13. 10.D 解析：由奇函数的定义验证可知②④正确．又()f x 是R 上的奇函数，∴ ()00＝f .∵ ()f x 在 上是增函数，且()0＞f x ， ∴ ()f x )在 － 上也是增函数，且()0＜f x .又[]24x ,∈时，()0＝－(－4)＞f x f x ，且()f x 为减函数． 同理()f x 在[4,6]为减函数且()0＜f x .如图所示．∵ 0(－25)＝(－1)＜f f ，()()011＝3＞f f ，()()0008＝＝f f ， ∴ ()()0(－25)＜8＜11f f f ． 13. (1)⎝⎛⎦⎤－∞，3a (2)(－∞，0)∪(1,3] 解析：(1)当 且 时，由 － 得，即此时函数 的定义域是⎝⎛⎦⎤－∞，3a ； (2)当 － ，即 时，要使 在 上是减函数，则需 － ，此时 . 当a －1<0，即a <1时，要使f (x )在(0,1]上是减函数，则需－a >0，此时a <0. 综上所述，所求实数 的取值范围是 － ， ． 14.25-解析: =()225f -=-.15.5 解析：∵ f (2x ＋1)＝3x －2＝32(2x ＋1)－72，∴ f (x )＝32x －72，∴ f (a )＝4，即 32a －72＝4，∴ a ＝5.16.（1，5） 解析：设 ＝ － ＋ ，则 ＝ ，即 ＝， ， ，作出 的图象如图所示，要使方程 － ＋ ＝ 有四个全不相等的实根， 需使函数 与 ＝ 的图象有四个不同的交点， 由图象可知， .第12题图24（2）由⎪⎩⎪⎨⎧≠>-≥+,0,02,032x x x 即3,22,0.x x x ⎧≥-⎪⎪<⎨⎪≠⎪⎩∴ 23- ＜ ，且 .故函数的定义域是 23-＜ ，且 ． 18.解：(1)因为 ∈Z ，所以函数图象是由一些点组成的，这些点都在直线 ＝ － 上．(如图①)(2)所给函数可化简为 ＝是一条折线．(如图②)19. (1)证法一：∵ 函数 对于任意 ， ∈R 总有 ＋ ＝ ＋ ，∴ 令 ＝ ＝ ，得 ＝ .再令 ＝－ ，得 － ＝－ ． 在R 上任取 ，则 － ， － ＝ ＋ － ＝ － ．又∵ 当 时， ，而 － ，∴ － ，即 ． 因此 在R 上是减函数． 证法二：设 ，则 －＝ － ＋ － ＝ － ＋ － ＝ － ．又∵ 时， ，而 － ，∴ － ，即 ， ∴ 在R 上为减函数．(2)解：∵ 在R 上是减函数，∴ 在 － 上也是减函数， ∴ 在 － 上的最大值和最小值分别为 － 与 ．而 ＝ ＝ ＝ － ， － － . ∴ 在 － 上的最大值为2，最小值为－2.20.解：(1) ∵ ＋ ＝－ ，∴ ＋ ＝－ ＋ ＝ ．∴ 是周期为4的周期函数．(2)当x ∈[－2,0]时，－x ∈[0,2]，由已知得f (－x )＝2(－x )－(－x )2＝－2x －x 2. 又f (x )是奇函数，∴ － ＝－ ＝－ － ，∴ ＝ ＋ . 又当x ∈[2,4]时，x －4∈[－2,0]，∴ f (x －4)＝(x －4)2＋2(x －4)．又 是周期为4的周期函数，∴ ＝f (x －4)＝(x －4)2＋2(x －4)＝x 2－6x ＋8. 从而求得x ∈[2,4]时，f (x )＝x 2－6x ＋8. (3) f (0)＝0，f (2)＝0，f (1)＝1，f (3)＝－1. 又f (x )是周期为4的周期函数，∴ ＋ ＋ ＋ ＝ ＋ ＋ ＋ ＝ ＝ ＋ ＋ ＋ ＝ .又(2012)(4503)(0)0,f f f =⨯==∴ ＋ ＋ ＋…＋ ＝0. 21.解：(1)设 ，则－ ，所以 － ＝－ －＋ － ＝－ － . 又 为奇函数，所以 － ＝－ ，于是 时， ＝ ＋ ＝ ＋ ，所以m ＝2. (2)要使 在 － ， － 上单调递增，结合 的图象知⎩⎪⎨⎪⎧a －2>－1，a －2≤1，。

课后导练基础达标1.一根弹簧，挂重100 N 的重物时，伸长20 cm ，当挂150 N 的重物时，弹簧伸长（ ）A.3 cmB.5 cmC.25 cmD.30 cm解析：由正比例关系知150100=x20,∴x=30. 答案：D2.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x 2,x ∈(0,240).若每台产品的售价为25万元，则保证生产者不亏本的最低产量为（ ）A.100台B.120台C.150台D.180台解析：由⎩⎨⎧≤+<<25x,0.1x -20x 000 3240,x 02 即⎩⎨⎧≥+<<0,000 30-50x x 240,x 02得150≤x<240.答案：C3.某商店把原定价每台为2 640元的彩电以九折优惠售出时，仍可获利20%，那么这种彩电每台的进价是…（ ）A.1980元B.2000元C.2112元D.2200元解析：设每台进价为x 元,则2640×0.9=x(1+20%),得x=1980.答案：A4.在x 克a%的盐水中，加入y 克b%的盐水，浓度变成c%，则y 与x 的函数关系为（ ） A.y=b c a c --x B.y=cb ac --x C.y=c a c b --x D.y=a c c b --x 解析：由yx y b x a ++%%=c%, 即ax+by=cx+cy,∴y=cb ac --x. 答案：B5.已知等腰三角形的周长为20cm ，底边长y(cm)是腰长x(cm)的函数，则函数的定义域为（ ）A.(0,10)B.(0,5)C.(5,10)D.［5,10)解析：y=20-2x,由⎩⎨⎧>>0x 0,2x -20得0<x<10. 答案：A6.下表列出了一项试验的统计数据，下列函数关系式中，最能表示这组数据所表示的关系的A.y=xB.y=2x-2C.y=212-xD.y=21+x 解析：代入检验可选C.答案：C7.甲、乙两店出售同一商品所得利润相同，甲店售价比市场最高限价低10元，获利为售价的10%，而乙店售价比市场最高限价低20元，获利为售价的20%，那么商品的最高限价是（ ）A.30元B.40元C.70元D.100元解析：设最高限价是x 元,则由条件知(x-10)×10%=(x-20)×20%,即x-10=2(x-20),得x=30.答案：A8.某种商品2003年提价25%，2004年要恢复原价，则应降价（ ）A.30%B.25%C.20%D.15%解析：设原价为a ，降价的百分率为x ，则a(1+25%)(1-x)=a,得x=0.2.答案：C9.某水果市场规定,批发水果不少于100千克时,批发价为每千克2.5元,小王携带现金3 000元到市场采购苹果,并以批发价买进,如果购买的苹果为x 千克,小王付款后剩余现金y 元,则y 与x 之间的函数关系为_______.答案：y=3 000-2.5x,100≤x≤120010.邮局规定，邮寄包裹，在5千克内每千克5元，超过5千克部分按每千克3元收费，邮费与邮寄包裹重量的函数关系式为_______.答案：y=⎩⎨⎧>-+≤<5),5(325.50,5x x x x 综合运用11.电子技术迅速发展，计算机的成本不断降低，若每隔5年计算机的价格降低31，则现在价格为4050元的计算机经过15年后价格应降为_______. 解析：4050×(131-)3=4050×278=1200元. 答案：1200元 12.把长为12 cm 的细铁丝截成两段,各自围成一个正三角形,那么这两个三角形面积之和的最小值是_____.解析：设一个三角形边长为x cm,则另一个三角形边长为(4-x) cm,两个三角形的面积和为S=43x 2+43(4-x)2=23［(x-2)2+4］≥23cm 2. 当x=2 cm 时,S min =23cm 2.答案：23cm 213.国际上通常用恩格尔系数衡量一个国家和地区人民生活水平的状况,它的计算公式为n=yx (x:人均食品支出总额,y:人均个人消费支出总额),且y=2x+475.各种类型家庭如下: 家庭类型 贫困 温饱 小康 富裕n n≥59% 50%≤n<59% 40%≤n<50% 30%≤n<40% 李先生居住地2006年比1998年食品价格下降7.5%,该家庭在2006年购买食品和1998年完全相同的情况下人均少支出75元,则该家庭2006年属于…( )A.贫困B.温饱C.小康D.富裕解析：设1998年人均食品支出x 元,则2006年人均食品支出x(1-7.5%)=92.5%x(元).2006年人均个人消费支出2×92.5%x+475(元).依题意有2×92.5%x+475+75=2x+475.解之,得x=500.n=475%5.922%5.92+⨯x =14625.4≈33.04%. 答案：D14.某商店迎来店庆,为了吸引顾客,采取“满一百送二十,连环送”的酬宾促销方式,即顾客在店内花钱满100元(可以是现金,也可以是奖励券或二者合计),就送20元奖励券;满200元,就送40元奖励券;满300元,就送60元奖励券……当日花钱最多的一位顾客共花出现金70040元,如果按照酬宾促销方式,他最多能得到优惠( )A.17560元B.17540元C.17500元D.17580元解析：这位顾客花的70000元可得奖励券700×20=14000(元),只有这位顾客继续把奖励券全部消费掉,他才能得到最多优惠,但当他把14000(元)奖励券消费掉可得到140×20=2800(元)奖励券,消费2800元奖励券又可得到28×20=560(元)奖励券,560元再加上先前70040中的40元共消费600元应得奖励券6×20=120(元),120元奖励券消费时又得20元奖励券,所以他总共会得到14000+2800+560+120+20=17500(元)优惠.答案：C15.一辆汽车在某段路程中的行驶速度与时间的关系如下图所示.(1)求图中阴影部分的面积,并说明所求面积的实际含义;(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2 004 km,试建立汽车行驶这段路程时汽车里程表读数s 与时间t 的函数解析式,并作出相应的图象.解析：(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360.阴影部分的面积表示汽车在这5h 内行驶的路程为360km.(2)根据图有s=⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤+-<≤+-<≤+-<≤+-<≤+.54,2299)4(65,43,2224)3(75,32,2134)2(90,21,2054)1(80,1,200450tttttttttt这个函数的图象如图.拓展探究16.某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.(1)当一次订购量为多少个时，零件的实际出厂单价恰降为51元？(2)设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=f(x)的表达式.(3)当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1 000个，利润又是多少元？(工厂售出一个零件的利润=实际出厂单价-成本)解析：(1)设一次订购量为x个，则60-(x-100)×0.02=51,得x=550个.(2)P=f(x)=⎪⎩⎪⎨⎧≥N∈<<-≤<.550,51).(,550100,5062,100,60xxxxx(3)当一次订购500个时，该厂获得的利润为500(6250500-)-500×40=6000元.当一次订购1000个时，该厂获得的利润为1000×51-1000×40=11000元.。

描述：例题：高中数学必修1(人教B版)知识点总结含同步练习题及答案
第二章 函数 2.3 函数的应用（I）
一、学习任务
了解一次函数、二次函数模型的意义，并能进行简单应用．
二、知识清单
函数模型的应用
三、知识讲解
1.函数模型的应用
函数模型的概念
函数模型就是用函数知识对日常生活中普遍存在的成本最低、利润最高、产量最大、收益最好、用料最省等实际问题进行归纳加工，建立相应的目标函数，确定变量的取值范围，运用函数的方法进行求解，最后用其解决实际问题．
几种函数模型的增长速度比较
在区间 上，尽管函数 ， 和 都是增函数，但它们的增长速度不同，随着 的增大，指数函数 的增长速度会越来越快，会超过并远远大于幂函数 的增长速度，而 的增长则会越来越慢，因此总会存在一个 ，当 时，就有 ．
(0,+∞)y =(a >1)a x y =x (a >1)log a y =(a >0)x a x y =(a >1)a x y =(a >0)x a y =x (a >1)log a x 0x >x 0x <<log a x a a
x
向高 为的水瓶内注水，注满为止，如果注水量 与水深 的函数关系的图像如图所示，那
么水瓶的形状是（ ）
解：B
取 的中点 作 轴的垂线，由图可知，当水深 达到容量高度的一半时，体积大于一
H V
h OH E h h
高考不提分，赔付1万元，关注快乐学了解详情。

答案：A ． 分钟B ． 分钟C ． 分钟D ． 分钟B
3.50 3.75
4.00
4.25。

2.3 函数的应用（I ）（必修1人教B 版）建议用时 实际用时满分 实际得分45分钟100分一、选择题（本大题共6小题，每小题6分，共 36分）1.在自然界中，某种植物生长发育的数量y 与时间x 的关系如下表所示： x123…y1 3 5 …下面的函数关系式中，能表达这种关系的是( ) A.21y x =- B.21y x =-C.21xy =- D.215252y .x .x =-+ 2.用长度为24的材料围一矩形的场地，中间要加两道隔墙，要使矩形的面积最大，则隔墙的长度应为（ ）A.3B.4C.6D.123.从盛装20升纯酒精的容器里倒出1升酒精，然后 用水加满，再倒出1升酒精溶液，再用水加满，照这样的方法继续下去，如果第 次时共倒出了纯酒精 升，则倒出第 次时，共倒出了纯酒精 的表达式是（ ） A.19120()f x x =+ B ．1120()=f x x + C ．19120()（）f x x =+ D. 120()=f x x 4.某幢建筑物，从10 m 高的窗口A 用水管向外喷水，喷出的水流呈抛物线状（抛物线所在平面与墙面垂直）．如图所示，如果抛物线的最高点M离墙1 m ，离地面403m ，则水流落地点 离墙的距离 等于（ ） A.2 mB.3 mC.4 mD.5 m5.某学校要招开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x =（[]x 表示不大于 的最大整数）可以表示为（）A.10[]x y = B.310[]x y += C.410[]x y += D.510[]x y +=6. 一批材料可以建成200 m 长的围墙，现用这些材料在一边靠墙的地方围成一块矩形场地，中间隔成3个面积相等的矩形（如图），则围成的矩形最大总面积为（ ）A. 2 500 2mB. 250 2mC. 3 000 2mD. 3 500 2m二、填空题(本大题共3小题，每小题6分，共 18分)7.某种电热水器的水箱盛满水是200升，加热到一定温度可浴用.浴用时，已知每分钟放水34升，在放水的同时注水，t 分钟注水22t 升,当水箱 内水量达到最小值时，放水自动停止.现假定 每人洗浴用水65升，则该热水器一次至多可供 人洗澡.8.某商店进货单价为45元，若按50元一个销售，能卖出50个；若销售单价每涨1元销售量就减少2个，为了获得最大利润，此商品的最佳售价应为每个 元.9．建造一个容积为8立方米，深为2米的长方体无盖水池，若池底造价为120元/平方米，池壁造价为80元/平方米，则水池的总造价（元）y与池底宽（米）x 之间的函数关系式是 ____ ． 三、解答题（本大题共3小题，共46分） 10．（14分）北京市的一家报刊摊点，从报社买进《北京晚报》的价格是每份0.30元，卖出的价 格是每份0.50元，卖不掉的报纸可以以每份0.10元的价格退回报社．在一个月（按30天计算）里，有20天每天可卖出400份，其余10天每天只能卖出250份，但每天从报社买进的份数必须相同，这个摊主每天从报社买进多少份，才能使每月所获的利润最大？并计算他一个月最多可赚多少元．11.（16分）某桶装水经营部每天房租、工作人员工资等固定成本为200元，每桶水进价为5元，销售单价与日销售量的关系如下表： 销售单价（元） 67 8 9 10 11 12日销售量（桶）480 440 400 360 320 280 240请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？最大利润是多少？12.（16分）某商品在近30天内每件的销售价格（元）p与时间（天）t 的函数关系式是200251002530t ,t ,t p t ,t ,t .+<<∈⎧=⎨-+≤≤∈⎩N,N 该商品的日销售量Q （件）与时间t （天）的函数关系式是40030（＜，）Q t t t =-+≤∈N ，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？2.3 函数的应用(I)（必修1人教B 版）一、选择题题号 1 2 3 4 5 6 答案二、填空题7． 8． 9. 三、计算题 10. 11. 12.2.3 函数的应用(I)（必修1人教B 版）1.A 解析：将各组数据代入选项中，21y x =-总成立，故选A ．2.A 解析：设隔墙的长度为x （0＜x ＜6），矩形的面积为y ，则y =x ×2442x-=222122318()x x x -+=--+， ∴ 当x =3时，y 最大．故选A ．3.A 解析：∵ 第k 次时共倒出了纯酒精x 升，∴ 第k 次倒出后容器中含纯酒精为（20-x ）升,第k +1次倒出的纯酒精是2020x -升,所以倒出第k +1次时，共倒出了纯酒精201912020（）x f x x x -=+=+.故选A 4.B 解析：以抛物线所在平面与墙面的交线为y 轴，和水平面的交线为x 轴建立坐标系，则由题设条件知，抛物线的顶点坐标 403（1，），点 坐标为（0，10）． 于是可设抛物线的方程为24013（）y a x =-+． 将点A 坐标（0，10）代入该方程可求得a 的值为103-． ∴ 抛物线的方程为21040133（）y x =--+． 令y =0，得214（）x -=，∴ 31或x x ==-（舍去）．∴ 点B 的坐标为（3，0），故OB =3 m ，故选B ．5.B 解析：代入特殊值56、57验证即可得到答案．若x =56，y =5，排除C 、D ，若x =57，y =6，排除A ； 故选B ．6.A 解析: 设每个小矩形的高为a m ，则长为120043（)b a =-，记面积为 m 2， 则2320044200050（）（＜＜）S ab a a a a a ==∙-=-+， ∴ 当25a =时，max S =2 500（m 2）.∴ 围成的矩形面积的最大值为 m 2. 7.4 解析：设最多用 分钟，则水箱内水量2217111200234222（）y t t t =+-=-+， ∴ 当172t =时， 有最小值，此时共放水17289234⨯=（升）. ∵ 每人洗浴用水65升，∴ 可供4人洗澡．8.60 解析:设涨价x 元时，获得利润为 元，则 ，∴ 当 时， 取最大值，此时售价为60元． 9.4480320（)y x x=++解析：由池底宽为 米，由池底面积为4，得池底的长为4x米， 则1644120804480320(+)=（)y x x x x=⨯+⨯++ ． 所以水池的总造价 （元）与池底宽 （米）之间的函数关系式是4480320（)y x x=++（ ＞0）． 10.解：设摊主每天从报社买进 （250≤ ≤400， ∈N ）份，则每月共可销售（ ）份，每份可获利润0.20元，退回报社 份，每份亏损0.20元.依题意，得f （x ）=0.20（20x+10×250）-0.20×10（x-250）=2x+1 000，x ∈[250，400]． ∵ 函数f （x ）在[250，400]上单调递增，∴ 当x=400时，max （）f x =1 800（元）， 即摊主每天从报社买进400份时，每月所获得的利润最大，最大利润为1 800元．11.解：设每桶水在原来的基础上上涨 元，利润为 元，由表格中的数据可以得到，价格每上涨1元，日销售量就减少40桶，所以涨价 元后，日销售的桶数为 ＞ ， 所以 ＜ ＜ ，则利润 ，其中0＜ ＜13， 所以当 =6.5时，利润最大，即当每桶水的价格为11.5元时，利润最大值为1490元． 12. 解：设日销售金额为 （元），则y p Q =∙．∴222080002514040002530 t t ,t ,t y t t ,t ,t ⎧-++<<∈⎪=⎨-+≤≤∈⎪⎩N,N =2210900025709002530（)()t ,t ,t ,t ,t ,t .⎧--+<<∈⎪⎨--≤≤∈⎪⎩N N 当0＜ ＜25， ∈N ， =10时， =900（元）； 当25≤ ≤30， ∈N ，t=25时， =1 125（元）．因为1 125＞900，知 1 125（元），且第25天，日销售额最大.。

高中数学学习材料唐玲出品第二章函数（必修1人教B版）A ．(，1)B ．(1，)C ．(，1]D ．[1，)-∞+∞-∞+∞ 9. 关于 的一元二次方程的两个实数根分别是 , ,且=7，则的值是( )A.1B.12C.13D.25 10.已知＝()y f x 是定义在R 上的奇函数，则下列函数中为奇函数的是( )①()＝y f |x|；②＝(－)y f x ；③＝()y xf x ； ④y ＝f (x )＋x . A ．①③ B ．②③ C ．①④D ．②④A.12-B.14- C ．14 D ．1212.已知定义在R 上的奇函数f (x ) 满足 － ＝－ ，且在区间 上是增函数，则( )A ．()()0－25＜11＜8f ()f fB ．()()08＜11＜(－25)f f fC ．()()011＜8＜(－25)f f fD ．()()0(－25)＜8＜11f f f二、填空题(本大题共4小题，每小题4分，共 16分)13.已知函数 f (x )＝3－axa －1(a ≠1)． (1)若 ，则 的定义域是________； (2)若f (x )在区间(0,1]上是减函数，则实数a 的取值范围是 .14.已知函数则.15．已知 ＋ ＝ － 且 ＝4，则 的值为__ ____．16. 已知方程 －4| |＋5＝ 有四个全不相等的实根，则实数 的取值范围是___ _． 三、解答题（本大题共6小题，共74分） 17．（12分）求下列函数的定义域：（1）xx x y -+=||)1(0；（2）xxx y 12132+--+=．18.（12分）作出下列各函数的图象： (1) ＝ － ， ∈Z ；(2＝－0)．19.（12分）已知函数对于任意x，y∈R，总有＋＝＋，且当时，，＝－错误！未定义书签。

.(1)求证：在R上是减函数；(2)求在－上的最大值和最小值．20.(12分)设是定义在R上的奇函数，且对任意实数，恒有＋＝－．当时，＝－.(1) 求证：是周期函数；(2) 当时，求的解析式；(3) 计算＋＋＋＋．21.（12分）已知函数＝是奇函数．(1)求实数m 的值；(2)若函数 在区间 － ， － 上单调递增，求实数a 的取值范围．22.（14分）已知22444（）f x x ax a a =-+--在区间[0，1]内有最大值-5，求a 的值及函数表达式（）f x ．第二章 函 数（必修1人教B 版）一、选择题二、填空题13． 14． 15. 16. 三、计算题 18.19.20.21.22.第二章 函 数 （必修1人教B 版）1. D 解析：由列表法表示的函数直接观察可得.2. D 解析: A 选项中的任意一个角总对应唯一的一个正弦值； B 选项中任意一个正方形的边长总对应唯一的一个面积；C 选项中任意的正n 边形边数（n ≥3）总对应唯一的顶点角度之和0(2）18n -∙︒； 故A ，B ，C 选项均为函数关系，而D 选项中的任意一个年龄对应的身高不唯一，故不是函数关系，故选D . 3.C 解析：因为函数()f x 的定义域为R ,所以 的取值范围也是 , 因此函数 ()()f x a f t +=的值域与函数()f x 的值域相同，都是 .4. A 解析：因为12220(－)(－)x x <，若12x x <，则有122x x <<，即2124－x x <<.又当2x >时，()f x 单调递增且(－)＝－(＋4)f x f x ，所以有()()211(4－)＝－f x f x f x <，即()()012＋f x f x <；若21x x <，同理()()012＋f x f x <，故选A.6.C 解析：距学校距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，后段直线段比前段下降的快，故C 图象吻合的最好. 7.D 解析：由函数单调性定义知选D.8. B 解析：由根式内部的代数式大于等于0求出集合M ，然后直接利用补集概念求解． 由01x -≥，得1x ≤，即（，1]M =-∞.又全集为R ，所以（1，）M =+∞ðR ．故选B . 9. C 解析：∵ 方程有两个实数根，∴ Δ ≥0, ∴ 或 .根据根与系数的关系得 .又 ＝ ，即 ＝ ，代入得到 - ,即 - , 解得 , (不合题意，舍去). 则关于 的一元二次方程为 , 根据根与系数的关系得 , ,所以 ＝ ＝ -4×（ ）＝13. 10.D 解析：由奇函数的定义验证可知②④正确．12.D 解析：∵，∴.又()f x 是R 上的奇函数，∴ ()00＝f .∵ ()f x 在 上是增函数，且()0＞f x ， ∴ ()f x )在 － 上也是增函数，且()0＜f x .又[]24x ,∈时，()0＝－(－4)＞f x f x ，且()f x 为减函数． 同理()f x 在[4,6]为减函数且()0＜f x .如图所示．∵ 0(－25)＝(－1)＜f f ，()()011＝3＞f f ，()()0008＝＝f f ， ∴ ()()0(－25)＜8＜11f f f ． 13. (1)⎝⎛⎦⎤－∞，3a (2)(－∞，0)∪(1,3] 解析：(1)当 且 时，由 － 得，即此时函数 的定义域是⎝⎛⎦⎤－∞，3a ； (2)当 － ，即 时，要使 在 上是减函数，则需 － ，此时 . 当a －1<0，即a <1时，要使f (x )在(0,1]上是减函数，则需－a >0，此时a <0. 综上所述，所求实数 的取值范围是 － ， ． 14.25-解析: =()225f -=-.15.5 解析：∵ f (2x ＋1)＝3x －2＝32(2x ＋1)－72，∴ f (x )＝32x －72，∴ f (a )＝4，即 32a －72＝4，∴ a ＝5.16.（1，5） 解析：设 ＝ － ＋ ，则 ＝ ，即 ＝， ， ，作出 的图象如图所示，要使方程 －＋ ＝ 有四个全不相等的实根， 需使函数 与 ＝ 的图象有四个不同的交点， 由图象可知，.第12题图24（2）由⎪⎩⎪⎨⎧≠>-≥+,0,02,032x x x 即3,22,0.x x x ⎧≥-⎪⎪<⎨⎪≠⎪⎩∴ 23- ＜ ，且 . 故函数的定义域是 23-＜ ，且 ． 18.解：(1)因为 ∈Z ，所以函数图象是由一些点组成的，这些点都在直线 ＝ － 上．(如图①)(2)所给函数可化简为 ＝是一条折线．(如图②)19. (1)证法一：∵ 函数 对于任意 ， ∈R 总有 ＋ ＝ ＋ ，∴ 令 ＝ ＝ ，得 ＝ .再令 ＝－ ，得 － ＝－ ． 在R 上任取 ，则 － ， － ＝ ＋ － ＝ － ．又∵ 当 时， ，而 － ，∴ － ，即 ． 因此 在R 上是减函数． 证法二：设 ，则 －＝ － ＋ － ＝ － ＋ － ＝ － ．又∵ 时， ，而 － ，∴ － ，即 ， ∴ 在R 上为减函数．(2)解：∵ 在R 上是减函数，∴ 在 － 上也是减函数， ∴ 在 － 上的最大值和最小值分别为 － 与 ．而 ＝ ＝ ＝ － ， － － . ∴ 在 － 上的最大值为2，最小值为－2.20.解：(1) ∵ ＋ ＝－ ，∴ ＋ ＝－ ＋ ＝ ．∴ 是周期为4的周期函数．(2)当x ∈[－2,0]时，－x ∈[0,2]，由已知得f (－x )＝2(－x )－(－x )2＝－2x －x 2. 又f (x )是奇函数，∴ － ＝－ ＝－ － ，∴ ＝ ＋ . 又当x ∈[2,4]时，x －4∈[－2,0]，∴ f (x －4)＝(x －4)2＋2(x －4)．又 是周期为4的周期函数，∴ ＝f (x －4)＝(x －4)2＋2(x －4)＝x 2－6x ＋8. 从而求得x ∈[2,4]时，f (x )＝x 2－6x ＋8. (3) f (0)＝0，f (2)＝0，f (1)＝1，f (3)＝－1. 又f (x )是周期为4的周期函数，∴ ＋ ＋ ＋ ＝ ＋ ＋ ＋ ＝ ＝ ＋ ＋ ＋ ＝ .又(2012)(4503)(0)0,f f f =⨯==∴ ＋ ＋ ＋…＋ ＝0. 21.解：(1)设 ，则－ ，所以 － ＝－ －＋ － ＝－ － . 又 为奇函数，所以 － ＝－ ，于是 时， ＝ ＋ ＝ ＋ ，所以m ＝2. (2)要使 在 － ， － 上单调递增，结合 的图象知⎩⎪⎨⎪⎧a －2>－1，a －2≤1，。