当前位置：文档之家 › 第十五次课 频率特性曲线

第十五次课 频率特性曲线

  • 格式：ppt
  • 大小：1.47 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

自动控制原理课件2第二节频率特性的几种表示方法

自动控制原理课件2第二节频率特性的几种表示方法
Sunday, April 15, 2012
6
Sunday, April 15, 2012
2
一、极坐标频率特性曲线（又称奈魁斯特曲线） 它是在复平面上用一条曲线表示ω 由 0 → ∞ 时的频率特性。 即用矢量 G ( jω ) 的端点轨迹形成的图形。 ω 是参变量。在曲线 的上的任意一点可以确定实频、虚频、幅频和相频特性。 根据上面的说明，可知： 频率特性曲线是S平面 ω Q(ω ) 上变量s沿正虚轴变化 时在G(s)平面上的映射。
第二节 频率特性的几种表示方法
Sunday, April 15, 2012
1
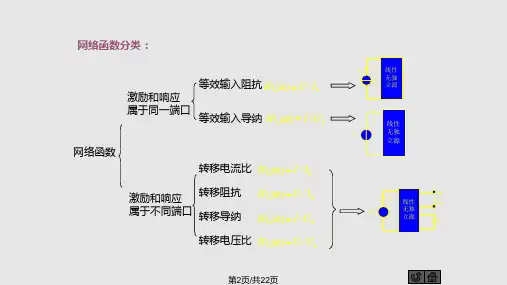
频率特性可以写成复数形式： ( jω ) = P(ω ) + jQ(ω ) ，也可 G 以写成指数形式：G ( jω ) =| G ( jω ) | ∠G ( jω )。其中，P(ω ) 为实 频特性， (ω ) 为虚频特性； G ( jω ) |为幅频特性， G ( jω ) 为相频 Q | ∠ 特性。 在控制工程中，频率分析法常常是用图解法进行分析和设 计的，因此有必要介绍常用的频率特性的三种图解表示。 极坐标频率特性曲线（又称奈魁斯特曲线） 对数频率特性曲线（又称波德图） 对数幅相特性曲线（又称尼柯尔斯图）
A(ω )
增益 0
Sunday, April 15, 2012
5
使用对数坐标图的优点： 可以展宽频带；频率是以10倍频表示的，因此可以清楚的 表示出低频、中频和高频段的幅频和相频特性。 可以将乘法运算转化为加法运算。 所有的典型环节的频率特性都可以用分段直线（渐进线） 近似表示。 对实验所得的频率特性用对数坐标表示，并用分段直线近 似的方法，可以很容易的写出它的频率特性表达式。 三、 对数幅相特性曲线（又称尼柯尔斯图） 尼柯尔斯图是将对数幅频特性和相频特性两条曲线合并成 一条曲线。横坐标为相角特性，单位度或弧度。纵坐标为对数 幅频特性，单位分贝。横、纵坐标都是线性分度。

频率特性图形表示

频率特性图形表示
性能分析（尤其是稳定性）时不需要绘制精确 的幅相特性曲线，只需绘制大致形状即可
G jH j
m2h
h
Ki j1i2j22ii j1
i1
i1
n2lv
l
jv jTi 1 Ti2j22iTi j1
i1
i1
（一） 放大环节（比例环节）
放大环节的传递函数为 G(s) K
其对应的频率特性是 G( j) K
当
1 T
时， G( j 1 )
T
1 0.707 G( j 1 ) 450
2
T
当 时， G( j) 0 G( j。) 900
当ω由零至无穷大变化时，惯性环节的频率特性在 G( j)平
面上是正实轴下方的半个圆周，证明如下：
G( j)
1
jT
1
1
1
T 2
2
T j 1 T 2 2
令
ReG
(
j
)
1
贝数，即 L() 20lg G( j) (dB) ；对数相频特性的纵轴也是
线性分度，它表示相角的度数，即 () G( j（) 度）。通常
将这两个图形上下放置（幅频特性在上，相频特性在下），且 将纵轴对齐，便于求出同一频率的幅值和相角的大小，同时为 求取系统相角裕度带来方便。
开环对数频率特性图(对数坐标图或Bode图) 包括 开环对数幅频曲线 和 开环对数相频曲线
G( j) G1( j)G2 ( j)Gn ( j) G( j) G1 ( j) G2 ( j) Gn ( j) L() 20 lg G( j) 20 lg G1( j) 20 lg G2 ( j) 20 lg Gn ( j)
（3） 用渐近线表示幅频特性，使作图更为简单方便；

频率特性的图示方法

频率特性的图示方法
对数相频特性：
由：
2.典型环节的Bode图
始于点（ωT ，0)，斜率20dB/dec的直线
对数幅频特性：
低频段（ω<<ωT）， 20lgG(j)20lgT－20lgT＝0dB
高频段（ω>>ωT）， 20lgG(j) 20lg－20lgT
故：
ωT : 转角频率
(5)一阶微分环节
对数相频特性：
=0， G(j)=0°；=T，G(j)=45°；=， G(j)=90°； 对数相频特性曲线对称于点(T，45°)
01
20lgG(j)＝ 20lg G(j)= 90o
02
对数幅频特性：过点（1，0）斜率20dB/dec的直线
03
对数相频特性：过点（0，90o ）平行于横轴的直线
04
2.典型环节的Bode图
始于点（ωT ，0)， 斜率－20dB/dec的直线
(4)惯性环节
令：
故：
对数幅频特性：
低频段（ω<<ωT）源自 20lgG(j)20lgT－20lgT＝0dB
02
补充必要的几点，根据G(j)、G(j)和Re[G(j)]、Im[G(j)]的变化趋势以及G(j)所处的象限，作出Nyquist曲线的大致图形。
03
2.绘制Nyquist图的一般方法
例1 系统的传递函数
解 系统的频率特性
0
幅频：
相频：G(j) = －90ｏ－arctgT
实频：
虚频：
积分环节改变了起始点（低频段）
根据上述特点，可以直接绘制系统的对数幅频特性
Bode图的绘制
步骤如下
写出开环频率特性表达式，将所含各因子的转折频率由大到小依次标在频率轴上

自动控制原理 频率特性图文PPT课件

自动控制原理 频率特性图文PPT课件

惯性环节的奈氏图
(1) 奈氏图
Im
传递函数和频率特性 绘取制特奈殊氏点图：近似方法:
ω ∞0
ω=0
ωω φφ ω=
=01 T
=∞
幅根频据G特幅A(sA((性频A)ωω(=ω((和特))ωω==)-=0))相性4==.07501T频和0oso7+特相11性频特性求出特G殊(jω点),=然后-将45它jω们T+1平ω1滑= 连1T接起来.
第23页/共106页
第二节 典型环节的频率特性
从图可知,当ζ较小时，对数幅频特性曲线出现了峰值，称为谐振峰值 Mr，对应的频率称为谐振频率ωr。
精确曲线与渐近线之间存在的误差与ζ值有关，ζ过大或过小，误差都 较大，曲线应作出修正。
dA(ω) =0
dω
可求得
(0≤ζ≤0.707)
代入得
Mr=A(ωr)=
Im
ω∞
0
Re
ω ω= 0
第8页/共106页
第一节 频率特性的基本概 念
2．对数频率特性曲线
L性也纵Φ特坐分性德特数线频称记((单是坐曲ωω性标度纵曲图性相组率为作由)位对标l)线=对g曲采。坐对线曲频成变.十 d。对2为数ω则的e数0线用标数又 线 。 化特倍c数l频表横分dg相的.为幅称 和 十性频幅lAB率g示坐度频横频(伯 对 倍曲程ω频ω特为标，特，，) -1---29842400000000
一、典型环节的频率特性 二、控制系统开环频率特性
第10页/共106页
第二节 典型环节的频率特性
1．比例环节
传递函数和频率特性
G(s)=K
G(jω)=K
幅频特性和相频特性
A(ω)=K
φ(ω)=0o

5-2频率特性曲线的绘制

5-2频率特性曲线的绘制

G (s) H (s)
1 1 1 K v 2 2 ( i s 1) ( i2 s 2 2 i i s 1) s Ti s 1 Ti s 2 iTi s 1
积分环节 一阶微分环节 二阶微分环节
2
比例环节
13:15
惯性环节
振荡环节
G( j )
1 Tj 1
A( )
1 1 T 2 2
,
( ) tg 1T
0时：A(0) 1， (0) 0
Im

Re 0

1 T
1 1 1 1 时：A( ) ， ( ) 45 T T T 2
0
时：A() 0， () 90
20log K 20log K
K 1 K 1 log
0 L( ) 20 lg K 常数 0
对数幅频特性：
K 1 K 1
相频特性：
( )
180
K 0

0 ( ) K 180
K 0 K 0
180
由图可见无论是欠 阻尼还是过阻尼系 统，其图形的基本 形状是相同的。 当过阻尼时，阻尼 系数越大其图形越 接近圆。
-2
0.2
13:15 16
（2）Bode图（对数频率特性）：
幅频特性为：
A( )
1 (1 T 2 2 )2 (2T )2
相频特性为：
( ) tg 1
2 T 1 T 2 2
L 对数幅频特性为： ( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2
低频段渐近线： 0时，L() 0 高频段渐近线： 时， L( ) 20 log (T 2 2 ) 2 40 log T 两渐进线的交点 o

5 第五章 频率特性及其图示

5 第五章 频率特性及其图示
s j
系统的频率特性就等于在系统传递函数 G(s)中以s=jω代入后所得的结果G(jω)。
频率特性的特点（2）
（2）G(jω)是以ω为自变量的复变函数
G( j ) G( )e j ( ) G( ) ( ) Re G( j ) j Im G( j )
幅频特性
极坐标
相特性曲线）。
OA 端点A形成轨迹曲线，称为Gj的极坐标图（幅
G( j ) G( j ) e
jG ( j1 )
当ω ： 时， 0
A
极坐标图

0
极轴
直角坐标
G( j ) R( ) jI ( )
jI
IA
极坐标图
A R
0
RA
在直角坐标上表示的曲线也称为极坐标图
两种坐标形式间的转换
G ( ) G ( j ) Re 2 ( ) Im 2 ( ) 1 Im( ) ( ) tg Re( )
Re( ) G( )cos ( ) Im( ) G( )sin ( )
极坐标图（Nyquist图）在直角坐标系或者极坐标系表示均可。
k
j 1)
G ( )
K ( i ) 2 1
m

k 1 i 1
i 1 n
(Tk ) 2 1
1
K a b
( ) tg ( i ) tg (Tk )
1 k 1
0：G(0) K；（0） 0
：G() 0；（） n m)90 （ K a)：n m 2 如 (T1j 1)(T2j 1) K b)：n m 3 如 (T1j 1)(T2j 1)(T3j 1)

频率特性几种表示方法.pptx

频率特性几种表示方法.pptx

2
第3页/共7页
二、对数频率特性曲线（又称波德图）
它由两条曲线组成：幅频特性曲线和相频特性曲线。 波德图坐标（横坐标是频率，纵坐标是幅值和相角）的分度： 横坐标分度：它是以频率 的对数值 log 进行分度的。所 以横坐标（称为频率轴）上每一线性单位表示频率的十倍变化， 称为十倍频程（或十倍频），用Dec表示。如下图所示：
Dec Dec Dec Dec
... 2 1
0 0.01 0.1
01
2
1 10 100
log பைடு நூலகம்
由于 以对数分度，所以零频率线在 处。
Sunday, November 24, 2024
3
第4页/共7页
纵坐标分度：幅频特性曲线的纵坐标是以log A()或20log A() 表示。其单位分别为贝尔（Bl）和分贝（dB）。直接将log A() 或 20log A() 值标注在纵坐标上。
工程上常用图形来表示频率特性，常用的有：
1．极坐标图，也称乃奎斯特(Nyquist)图。是以开环频率特性的
实部 为直角坐标横坐标，以其虚部 为纵坐标，以 为参变量的
幅值与相位的图解表示法。 2．对数坐标图，也称波德(Bode)图。它是由两张图组成，以lg 为横坐标，对数分度，分别以 20lg G( j) 和 ( j) 作纵坐 标的一种图示法。
Q( )
A( ) ( )
P( )
G(s)
s 1 s2 s 1
根据上面的说明，可知： 频率特性曲线是S平面 上变量s沿正虚轴变化 时在G(s)平面上的映射。
0 由于 | G( j) |是偶函数， 所以当 从 0 和0 变化时，乃奎 斯特曲线对称于实轴。
Sunday, November 24, 2024

频率特性和谐振现象.pptx

频率特性和谐振现象.pptx

U C
U | | Z|
X C
| 10 10 6 V 1460 0.046 mV 320
第17页/共22页
9.4 并联谐振电路
1 GCL并联谐振电路
基本要求：掌握GCL并联谐振电路的条 件和特点并与RLC串联谐振加以对比。
GCL并联电路的导纳为：
Y G j(C 1/L) G jB
实现谐振的条件是导纳的虚部为零，
0
1 LC
第13页/共22页
RLC串联电路的电流、电感电压和电容电压分别
为
I U R R
H
R
(
j )
U R
UC HC ( j)U
U L H L ( j)U
U L
I jL
U
1
jC
R U R
U C
RLC串联谐振电路
由上三式，可画出电流 I 和电压UC、UL随频率变动的曲线[下图(a)]， 以及谐振时的相量图［下图(b)］（以电流为参考相量）
2 电感线圈和电容器构成并联谐振电路，即 RL与C并联谐振电路。
电路模型如右图，等效复导纳为
I U
IC R IL jL
1/jC
Y 1 jC
R
j[C
L
线圈与电容并联谐振
]
R jL
R2 (L)2
R2 (L)2
产生谐振的条件是导纳的虚部为零。因此谐振时电容为
C0
R2
L (L)2
当改变频率时，可得谐振角频率：
RLC串联电路
| H L ( j) |
1
1
0
2
2
1 Q2
0
2
L
()
arctan

第4章(2)频率特性的图示分析

第4章(2)频率特性的图示分析

40db 20db 0db -20db --40db
G(s)=10s
0.1 0.2
12
[+20]
ω
10 20
100
G(s)= s
G(s)=0.1s
jik 06
14
Im [G(j)]
(4)惯性环节
o
传递函数： G(s) 1
∞ 5
Ts 1
频率特性： G(
j)
1
Tj 1
1
1 T 22
T j 1 T 22
0
dB
20lgK 0.1 1 10
对数相频特性：与0o线重合
0 0.1 1 10
(s -1) (s -1)
(2)积分环节
Im [G(j)]
传递函数： G(s)=1/s
频率特性： G( j) 1 0 j 1
j
幅频： |G(j)=1/
∞， =0时 0，→∞时
= ∞
Re
相频：∠G(j)=-90° 滞后90°
Im 传递函数： G(s)=K
[G(j)]
频率特性： G(j)=K
幅频：|G(j)|=K 20lg | G( j) | 20lg K o
K>1，则放大； K<1，则抑制 相频：∠G(j)=0° 系统响应无滞后
K Re
实频： U()=K 实频和虚频便于确定图形位置
虚频： V()=0
Nyquist图形：实轴上一定点，坐标为(K , j0) 对数幅频特性： 过点(1，20lgK)的水平线
1 Re 0
幅频 G( j) 1 1 T 2 2
相频 G( j) arctanT
实频
U
(
)
1

自动控制原理频率特性及其表示法ppt课件

自动控制原理频率特性及其表示法ppt课件
系统中的储能元件引起的。
实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真，
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
1 频率特性的基本概念
频率特性的求取
根据定义求取 对已知系统的微分方程，把正弦输入函数代
入，求出其稳态解，取输出稳态分量与输入正弦 量的复数比即可得到。
系统频率特性能间接地揭示系统的动态特性和 稳态特性，可简单迅速地判断某些环节或参数对系 统性能的影响，指出系统改进方向。
频率特性可以由实验确定，这对于难以建立动 态模型的系统来说，很有用处。
自动控制原理
2
5.1 频率特性及其表示法
1 频率特性的基本概念 2 频率特性的表示
自动控制原理
3
5.1 频率特性及其表示法
5.1 频率特性及其表示法 5.2 典型环节的频率特性 5.3 系统开环频率特性的绘制 5.4 用频率特性分析控制系统的稳定性 5.5 系统瞬态特性和开环频率特性的关系 5.6 闭环系统频率特性 5.7 系统瞬态特性和闭环频率特性的关系
自动控制原理
1
第5章 频域分析法
频率特性是控制系统在频域中的一种数学模 型，是研究自动控制系统的一种工程方法。
这个单位长度代表10倍频的距离，称之为 “十倍频”或“十倍频程”。
❖ 纵坐标用普通比例尺标度。
自动控制原理
21
A()
100
A
增 10
加
10 1
倍
0.1 0.01
自动控制原理
对数频率特性
L()
40
20 L 增加 20 dB
0
_20
_ 40 0.1

频率特性的图示

频率特性的图示
s p
40 20 0 -20 -40
dB 20 lg G
T
1
(s-1)
G
T (s-1)
微分 方程 系统
s j
p j
传递 函数
jik 07
频率 特性
9
实例2.3 测控器件动作元件模型 RCL电网络与质量弹簧阻尼的结合， 输入u(t),输出x(t) 各环节方程
1 u (t ) i1 (t ) R ∫ (i1 (t ) i (t )) dt C 1 (t ) k1 x (t ) (i1 (t ) i (t ))dt Li ∫ C U ( s) RI 1 ( s) LsI ( s) k1 sX ( s ) 1 I ( s) [U ( s) RI1 ( s) k1sX ( s)]① Ls 1 ( I 1 ( s ) I ( s )) LsI ( s ) k1 sX ( s ) Cs 1 I1 ( s ) Cs[( Ls ) I ( s ) k1sX ( s )]② Cs
三种数学模型的关系微分方程频率特性系统传递函数jik0710实例23测控器件动作元件模型rcl电网络与质量弹簧阻尼的结合输入ut输出xt各环节方程rcl网络线圈反电势为cslscscslsdtdtjik0711质量弹簧阻尼系统通电线圈对衔铁所产生的力fcsmscsmscsmscsmscsmscslsklrcklrclcrmjik07121nyquist图的作法

2
j v
(3)在原点附近，系统的 奈氏图为一旋紧的螺旋线。 例2: 作 Nyquist图
u
纯惯性环节 1 G( s) s( s 1)(2s 1) 带延时的 1 惯性环节 G( j ) j (1 j )(1 j 2 ) 3 1 2 2 ( j ) 2 2 2 2 (1 )(1 4 ) (1 )(1 4 ) 1 o 1 1 G ( j ) G ( j ) -90 tg tg (2 ) 1 2 1 (2 ) 2 o Im [G( j)] G ( j 0 ) , G ( j 0 ) 90 特殊点：ω=0∶

第十五次课频率特性曲线

第十五次课频率特性曲线

K
低频段或低频段的延长线在=1时的幅值为20lgK
La ()(dB)
La ()(dB)
20lgK
-40dB/dec
20lgK
-40dB/dec
1
0
1 K1/2

0
1 1 K1/2

按转折频率由低频到高频的顺序，在低频 渐近线的基础上，每遇到一个转角频率，根据 环节的性质改变渐近线斜率，绘制渐近线，直 到绘出转折频率最高的环节为止。
La ()(dB)
20lgK
-20dB/de1
0
1
K

0
1
1
K

(3) II型系统的低频起始段的绘制
当处于低频段时II型系统传递函数 G(s)H (s) K s2 系统Bode图低频段渐近线的斜率为-40dB/dec
低频段渐近线或其延长线与横轴相交，交点处频率
La ()(dB)
20lg K
0
1

(2) I型系统的低频起始段的绘制
当处于低频段时I型系统传递函数 G(s)H(s) K s 系统Bode图的低频段渐近线斜率为-20dB/dec
低频段渐近线或其延长线与横轴相交，交点处频率 =K
低频段渐近线或其延长线在=1时的幅值为20lgK
La ()(dB)
下次课程的主要内容
△*Nyquist稳定判据及应用
20
17
0
-4.3 0.1
-20dB/dec
11.5
1
7 10

-40dB/dec
在 1时的高度为:
20lg 7 17 转折频率：
( )()
0.1
1
0

对数频率特性曲线

对数频率特性曲线
自动控制原理
第五章 频域分析法－频率法
第五章 线性系统的频域分析法
5.1 频率特性 一、基本概念 信号可表示成不同频率正弦信号的合成。频率特性 能够反映不同频率的正弦信号作用下系统的性能。
r(t) 系统 css(t)
自动控制原理
第五章 频域分析法－频率法
一个稳定的系统，假设有一正弦信号输入
r(t ) Ar sint
A
自动控制原理
第五章 频域分析法－频率法
（1）幅相频率特性曲线（极坐标图/幅相曲线）
频率特性
(j ) (j ) (j ) M( )( )
幅相曲线：从0→∞变化时，φ(jω)在复平面
上划过的轨迹。
复 G( j)与G( j)
平 面
关于实轴对称。
自动控制原理
第五章 频域分析法－频率法
• 1）对数幅频曲线关于0dB线（ω轴）对称， • 2）对数相频曲线关于0°线（ω轴）对称。 •如
1 s 1 Ts 1
与s 与 Ts 1
自动控制原理
第五章 频域分析法－频率法
• （3）振荡环节和二阶微分环节
稳定系统的频率特性可由实验的方法确定。
自动控制原理
第五章 频域分析法－频率法
频率特性、传递函数、微分方程间的关系：
图5-4 线性系统数学模型间的关系
自动控制原理
第五章 频域分析法－频率法
• 例 设系统的传递函数为
G(s) 1 0.5s 1
• 试求输入信号 r(t) 10sin 6.28t时，系统的稳态输
1
s s j j
j 1 1 90o

j
0
a、幅相频率特性曲线
A 1 L( )=-20lg

频率特性2

频率特性2

可以清楚地看出在整个频率
范围内，()呈滞后持续增加的 趋势，极限为-90。 对数相频特性曲线将对应于 ω=1/T及 ()=-45°这一点斜对 称。
当惯性环节的时间常数T改变时，其转 折频率1/T 将在Bode图的横轴上向左或向 右移动。与此同时，对数幅频特性及对数 相频特性曲线也将随之向左或向右移动， 但它们的形状保持不变。
()=0º ，表示输出与输入同相位，
既不超前也不滞后。
2、惯性环节 幅相频率特性图/奈氏图： 1 传递函数 G ( s ) Ts 1
1
T 2 2 j 2 2 频率特性 G( j ) jT 1 T 1 T 1 1
幅频特性
A( )
相频特性
1 1 (T )
（1）横坐标按频率取对数分度，低频部分 展宽，而高频部分缩小 。与对实际控制系统 （一般为低频系统）的频率分辨要求吻合。 （2）幅频特性取分贝数［20LgA(ω)］后，
使各因子间的乘除运算变为加减运算，在Bode
图上则变为各因子幅频特性曲线的叠加，大大
简化了作图过程，使系统设计和分析变得容易。
G(j)=G1(j)G2(j)…Gn(j)= A()ej() 式中 A()=A1()A2()…An()；
横坐标对于ω是不均匀的，但对lgω却是均匀的线性分度。由 于0频无法表示，横坐标的最低频率是由所需的频率范围来确定的。 而是lgω2-lgω1 ，如2与20、10与100之间的距离均为一个单位长度， 即一个十倍频程。
纵坐标（幅频特性）是 对幅值分贝(dB)数进行分度， 用L()=20 lgA(ω)表示。 对数相频特性图的横坐 标分度方法同对数幅频特性， 而纵坐标则对相角进行线性 分度，单位为度（o） ,仍用 ( )表示。

频率特性及其图示法

频率特性及其图示法

幅
值 比
r=sinωt
1
R(s)
0.5s 1 Y(s)
ω=0.2π ω=1π
ω=5π
考
ω=0.2π
察
相
位
差
ω=1π
ω=5π
结论 推广到一般，得出以下
：
1、对稳定的线性系统作用正弦信号，其稳态输出
仍是一正弦函数，频率不变，幅值和相位发生变化。
2、幅值比 B 和相位差Φ都是输入信号频率ω的函数，
A
2
整理：U
2
V
2
KU
经配方，
即：
U
K 2
2
U V 2
K 2
2
圆的方程。圆心 (K/2, j0),半径K/2。
A是幅值，ω是角频率.
稳态响应
，是频率的函数。
利用频率特性研究的系统必须是稳定的系统。
一阶线性系统
r=Asinωt
K
R(s)
Ts 1
Y(s)
当输入
r Asint时， R(s)
A s2 2
Y (s) G(s)R(s)
K A Ts 1 s2 2
K
A
b a a
Ts 1 (s j )(s j ) Ts 1 s j s j
A
∴ G( j) 是频率特性函数。
关于频率特性的总结：
1、任何稳定的线性系统，当输入为正弦信号时，稳 态后输出也是正弦信号，频率相同，幅值和相位 都发生变化，而且它们都是频率的函数。
2、将传递函数 G(s)中的s 用 j 代替得 G( j) , G( j)
即为频率特性。 G( j) 为幅值比，又称幅频特性。 G( j) 为相位差，又称相频特性。

自动控制原理频率特性曲线讲解

自动控制原理频率特性曲线讲解

40db
[-20]
20db
L(ω)曲线
G(s)H(s)

40(0.5s 1) s(2s 1)( 1 s
1)
30
[-40]
0db
0.1
0.5 1
2
[-20]
10
30
100
ω
-20db
[-40]
--40db
40 低频段： S
0.1 时为52db
0.5时为38db
转折频率：0.5 2 30
0
1
Re[G(jω)]
L(ω)
90o
一阶微分L(ω)
40db
45o
20db
0db 0o -8db -20db
0.1 0.2
12
[+20]
ω
10 20
100
--40db
G(s) 0.5s 1 G(s) ?
返回
G(s)

s2

n2 2 n s

n2
Im[G(jω)]
振荡环节G(jω)
惯性环节L(ω)
G(s) 1
G(s) 10
40db
0.5s 1
s4
20db 8db 0db 0o
-20db
45 o
--40db
0.1 0.2
12
[+20]
ω
10 20
100
90 o
返回
Im[G(jω)] 惯性环节1G(jω)
0
1
Re[G(jω)]
Im[G(jω)] 惯性环节2G(jω)
12
ω
10 20
100
--40db
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
La ( )( dB ) La ( )( dB )
20lgK 20lgK 0 1
-20dB/dec
-20dB/dec
1
K

0
1
1
K

(3) II型系统的低频起始段的绘制
当处于低频段时II型系统传递函数 G( s) H ( s) K s 2 系统Bode图低频段渐近线的斜率为-40dB/dec
La (0 )
C:取 La 为特殊值 0，则 (0 )
0 K
1
1
1
1
K

(1) 0型系统的低频起始段的绘制 当处于低频段时0型系统传递函数 G ( s ) H ( s ) K 低频段高度H=20lgK（dB）
La ( )( dB )
20 lg K
0
1

(2) I型系统的低频起始段的绘制 当处于低频段时I型系统传递函数 G ( s ) H ( s ) K s 系统Bode图的低频段渐近线斜率为-20dB/dec 低频段渐近线或其延长线与横轴相交，交点处频率 =K 低频段渐近线或其延长线在=1时的幅值为20lgK
r
Gr (s)

系统开环 于各环节 之和；相 节的相位
()
r L() 20lg Ai () i 1 r

20lg A ()
i i 1
r
()
k k 1
开环对数幅频曲线及相频曲线分别由各串联环节 对数幅频曲线和相频曲线叠加而成。 典型环节的对数渐近幅频曲线为不同斜率的直线 或折线，故叠加后的开环渐近幅频特性曲线仍为不 同斜率的线段组成的折线。 因此，首先确定低频起始段的斜率和位置，然后 确定线段转折频率（交接频率）以及转折后线段斜 率的变化，那么，就可绘制出由低频到高频的开环 对数渐近幅频特性曲线。
系统开环对数频特性曲线的绘制
控制系统一般由多个环节组成，在绘制系 统Bode图前，应先将系统传递函数分解为典 型环节乘积的形式。
b0 s m b1s m 1 bm 1s bm G( s) H ( s) s n a1s n 1 a n 1s an
步骤：
开环增益K的确定
由 =1 作垂线与低频段 (或其延长线)的交点的分贝 值=20lgK(dB)，由此求出K值。
低频段斜率为 -20dB/dec ，低频段 ( 或其延长线 ) 与0dB线交点处的值即等于K1/ 。 其他几种常见情况如下表所示
A sin t
信号源
对象
记录仪
对实验测得的系统对数幅频曲线进行分段处理， 即用斜率为20dB/dec整数倍的直线段来近似测量到 的曲线。 当某处系统对数幅频特性渐近线的斜率发生变化 时，此即为某个环节的转折频率，此环节依据斜率 的变化来确定。 系统最低频率段的斜率由开环积分环节个数决定。 低频段斜率为-20dB/dec,则系统开环传递函数有 个积分环节，系统为型系统。
17
-4.3
0
20
11.5
0.1 1
7 10
-40dB/dec

( )()
0 0.1 1 10

-135
-180
-90
例：请绘制以下系统的Bode图
（1） G( s)
50000 ( s 10) s( s 1)(0.005s 1)(s 500)
10( s 100) （2） G( s) 2 s 2s 100
A:在 内任选一点 ω 0,计算其值。 min
（若采用此法，推荐取ω 0＝ω 1）
低频起始段的绘制
B:取特定频率ω 0＝1，则
La (1) 20 lg K
1
La (0 ) 20lg K 20 lg0
20 lg K 20 lg K
0
La ( )( dB )
－20dB/dec
2 2 K ( 1s 1)( 2 s 2 2 j 2 s 1)
s (T1s 1)(T22 s 2 2 2i T2 s 1)
依据传递函数确定各环节的转折频率,并将 转折频率由低到高依次标注到半对数坐标纸横 轴上（不妨设为：ω 1、ω 2、ω 3……）
低频段特性取决于 K ，直线斜率为－ 20dB/dec。 s 为获得低频段，还需要确定该直线上的一点，可以采 用以下三种方法：
如需要精确对数幅频特性，则可在各转折 频率处加以修正。
相频特性曲线由各环节的相频特性相加获 得。 低频段： 高频段： ( 90 ) ( n m) ( 90) 注意：对数幅频特性曲线上要标明斜率！
L( )(dB )
例：
-20dB/dec
7 G ( s) s (0.087s 1) 初端斜率： 1 斜率 20dB / dec 在 1时的高度为: 20 lg 7 17 转折频率： 1 / 0.087 11.5
低频段渐近线或其延长线与横轴相交，交点处频率 K 低频段或低频段的延长线在=1时的幅值为20lgK
La ( )( dB ) La ( )( dB )
20lgK
-40dB/dec
20lgK
-40dB/dec
1
0 1 K1/2

0
1
1
K1/2

按转折频率由低频到高频的顺序，在低频 渐近线的基础上，每遇到一个转角频率，根据 环节的性质改变渐近线斜率，绘制渐近线，直 到绘出转折频率最高的环节为止。
10( s 3) （3） G( s) s( s 2)( s 2 s 2)
由Bode图确定系统的传递函数
由 Bode 图确定系统传递函数，与绘制系统 Bode图相反。即由实验测得的Bode图，经过分 析和测算，确定系统所包含的各个典型环节，从 而建立起被测系统数学模型。 最小相环对数 频率特性图(Bode图） 2、对数坐标图与传递函数 的关系
5-4 系统开环对数频率特性曲线 的绘制
系统开环传函由多个典型环节相串联：
G(s) H (s) G1 (s)G2 (s)
r j k ( ) G ( j ) H ( j ) Ai ( )e k 1 i 1