卡诺图化简方法.pdf

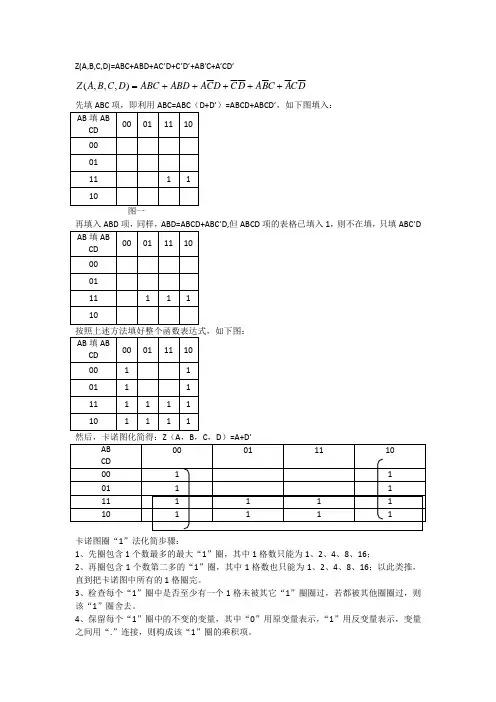
Z(A,B,C,D)=ABC+ABD+AC’D+C’D’+AB’C+A’CD’+++Z+BA=,(,,)C+BACADCDCABDABCACDD先填ABC项，即利用ABC=ABC（D+D’）=ABCD+ABCD’，如下图填入：图一’D,但ABCD项的表格已填入1，则不在填，只填ABC’D按照上述方法填好整个函数表达式，如下图：卡诺图圈“1”法化简步骤：1、先圈包含1个数最多的最大“1”圈，其中1格数只能为1、2、4、8、16；2、再圈包含1个数第二多的“1”圈，其中1格数也只能为1、2、4、8、16；以此类推，直到把卡诺图中所有的1格圈完。

3、检查每个“1”圈中是否至少有一个1格未被其它“1”圈圈过，若都被其他圈圈过，则该“1”圈舍去。

4、保留每个“1”圈中的不变的变量，其中“0”用原变量表示，“1”用反变量表示，变量之间用“.”连接，则构成该“1”圈的乘积项。

5、一个“1”圈对应一个乘积项，有多少“1”圈，就有多少乘积项，它们之间用“+”连接。

例题2：Y(A,B,C,D)=m1+m5+m6+m7+m11+m12+m13+m15解：1、在卡诺图中填充好函数表达式，如下图：4、圈完所有的1格，通过检查，发现原来圈4个1格的最大“1圈”中所有的1格都被其6、按照写化简后的函数逻辑表达式的规则，得化简后的函数表达式：Y（A,B,C,D）=A’C’D+ABC’+ ACD+A’BCABC’ACD A’BC。

m0
0
m1如何根据输入1变量组 m2合写出相应最2小项？
m3
3
m4
4
m5
5
m6
6
m7
7
例如 ABC 101 5 m5
m4 4 100 ABC
2. 最小项的基本性质
(1) 对任意一最小项，只有一组变量取值使它的值为1，而
其余各种变量取值均使其值为0。 (2) 不同的最小项，使它的值为1的那组变量取值也不同。 (3) 对于变量的任一组取值，任意两个最小项的乘积为0。 (4) 对于变量的任一组取值，全体最小项的和为1。
每一个与项都是最小项的与或逻辑式称为标 准与或式，又称最小项表达式。
任何形式的逻辑式都可以转化为标准与或式， 而且逻辑函数的标准与或式是唯一的。
[例] 将逻辑式 Y ABC AB C D 化为标准与或式。
解：(1) 利用摩根定律和分配律把逻辑函数式展开为与或式。
Y ABC AB C D ABC AB (C D) ABC ABC ABD 普通与或式，非标准与或式
CD
AB
C D CD CD C D
同一行最 左与最右 AB ABC D ABCD ABCD ABC D
方格相邻
AB ABC D ABCD ABCD ABC D 卡诺图特点： 循环相邻性 AB ABC D ABCD ABCD ABC D
同一列最 上与最下 ቤተ መጻሕፍቲ ባይዱ格相邻
AB ABC D ABCD ABCD ABC D
(2) 找出真值表中Y=1 对应的最小项，在 卡诺图相应方格中 填1，其余不填。
BC A 00 01 11 10
0 10 1 3 12
1 14 5 7 16
已 [例] 已知 Y AD AB(C BD)，试画出Y的卡诺图。 知 解：(1) 将逻辑式转化为与或式

精品课件
26
输入变量ABC取值为001、010、100时，
逻辑函数Y有确定的值，根据题意，有任一命令（正 转、反转和停止）时为1，否则为0。
反变 函换 数为
CD BD
CD
AB
00 01 11 10
Y AB AC BD CD AB
00 1
0
1
1
01 1
0
0
1
11 0
0
0
0
10 0
0
1
1
AC
精品课件
13
4、卡诺图的性质
（1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C
但是，若 F= ABCD+ABC+BC+ABC ，显然，该函数式
难于找到相邻项。
精品课件
1
2.4.2 逻辑函数的标准式——最小项表达 式
问题的提出：逻辑函数 F= ABC+ABC ，之所以易于看出它们 的乘积项是逻辑相邻项，是因为它们的每一个乘积项中都包 含了所有的变量。而F= ABCD+ABC+BC+ABC，每个乘积项没有 包含所有的变量，所以逻辑相邻关系不直观。于是引入了最 小项的概念。
15
AB CD
00 01 11 10
00 0
1
1
0
01 1 0 0 1
11 1
0
0
1 ＡＤ
10 0 1 1 0
ＢＤ
AB CD
00 01 11 10
00 1
0
0
1
01 0
1
1
0
11 0

ABC ABC A BC
m3 m2 m1
m(1、 2、 3)
例2
L( ABC ) ( AB AB C ) AB
AB AB C AB
AB AB C AB ( AB AB) C AB ABC ABC AB(C C) ABC ABC ABC ABC
⒈用摩根定律去掉非号(多个变量上)直至只在一个变量上有非号为止
⒉用分配律去除括号，直至得到一个与或表达式
⒊配项得到最小项表达式
习 例1
题
A B A BC
的最小项
求函数F(A、B、C) 表达式 解：F(A、B、C)
A B A BC
A B A BC
AB(C C) A BC
如:
m0 m2 m4 m6 m8 m10 m12 m14 D
2.用卡诺图化简逻辑函数的方法和步骤
设已得到逻辑函数的卡诺图
1) 将相邻的值为“1”的小方块画成若干个包围圈
ⅰ)每个包围圈中必须含有2n个小方块 (n=0,1,2, …)
画 圈 原 则
ⅱ)小方块可重复被包围，但每个包围圈中必须含有其他 包围圈没有的新小方块 ⅲ)不能漏掉任何值为1的小方块 ⅳ) 包围圈所含的小方块数目要尽可能多 ⅳ) 包围圈数目要尽可能少，画包围圈的顺序由大→小
10 1
01 11 10
1 1 1 1 1 1 1 1 1
B
1 1 1
D
3.具有无关项的逻辑函数的卡诺图化简
无关项的定义
在真值表内对应于变量的某些取值下，函数的值可以是任意的，或者 这些变量的取值根本不会出现，这些变量取值所对应的最小项称为无 关项或任意项。

26
(7) 由最大项表达式求最简与或式
例2.6.18 已知函数 F ( A, B,C, D) M (5,7,13,15)
求最简与或式。
CD AB 00 01 11 10
00 1 1 1 1 01 1 0 0 1 11 1 0 0 1 10 1 1 1 1
F(A,B,C,D) = B + D
图 2.6.18
16
(4) 合并的规律 ① 圈2格，可消去1个变量；
BC A 00 01 11 10
0 1 1 00 1 0 0 00
BC
A
00 01 11 10
0 1 0 01
1 0 0 00
F=AB
F=AC
17
② 圈4格，可消去2个变量；
ห้องสมุดไป่ตู้
BC
A
00 01 11 10
0 1 1 00
1 1 1 00
BC A 00 01 11 10
例2.6.16 化简函数
F( A, B,C, D) m(0,2,5,6,7,8,9,10,11,14,15)
为最简与或式。
CD AB 00 01 11 10
00 1 0 0 1 01 0 1 1 1 11 0 0 1 1 10 1 1 1 1
图 2.6.15
F(A,B,C,D) = A B D + BD+AB+BC
BC A 00 01 11 10 ⊕0 0 1 1 0
1 0 0 00
BC A 00 01 11 10 ﹦ 0 0 0 10
1 0 1 00
11
(4) 反演 BC
A 00 01 11 10
0 0 1 00 1 0 1 00

二变量卡诺图
三变量的卡诺图
• 4变量的卡诺图
五变量的卡诺图
用卡诺图表示逻辑函数
1. 将函数表示为最小项之和的形式 mi 。
2. 在卡诺图上与这些最小项对应的位置上添入1 ，其余地方添0。
用卡诺图表示逻辑函数
Y (A, B,C, D) ABCD ABD AB
ABCD (C C)ABD AB[(CD) CD CD CD]
2.8 多输出逻辑函数的化简
例: Y1(A, B,C, D) (1, 4,5, 6, 7,10,11,12,13,14,15)
Y2 (A, B,C, D) (1,3, 4,5, 6, 7,12,14) Y3( A, B,C, D) (3, 7,10,11)
卡诺图化简
Y1( A, B,C, D) B AC ACD Y2 ( A, B,C, D) AD BD
m(1, 4据：具有相邻性的最小项可合并，消去 不同因子。
在卡诺图中，最小项的相邻性可以从图形 中直观地反映出来。
合并最小项的原则：
两个相邻最小项可合并为一项，消去一对因子
四个排成矩形的相邻最小项可合并为一项，消去 两对因子
在输入变量某些取值下，函数值为1或 为0不影响逻辑电路的功能，在这些取 值下为1的最小项称为任意项
逻辑函数中的无关项：约束项和任意项可以写
入函数式，也可不包含在函数式中，因此统称 为无关项。
2.7.2 无关项在化简逻辑函数中的应用
合理地利用无关项，可得更简单的化简结果。
加入（或去掉）无关项，应使化简后的项数最少， 每项因子最少······
CD
AB 00 01 11 10 00 1 0 0 1 01 1 0 0 1 11 1 1 1 1 10 1 1 1 1

Y ( A, B, C , D ) ABC ABCD ABCD ABCD 约束条件：A ⊙ B＝0
逻辑函数中的无关项
• 无关项在逻辑函数化简中的作用：
– 例2：用卡诺图简化下列逻辑函数，并写成最 简与或式和或与式。
Y ABC ABCD ABCD ABCD CD AB 00 约束条件：A B＝0 00 × 约束条件可表示为：AB AB 0 01 1
逻辑函数中的无关项
• 约束项：
– 表示方法：
ABC 0 ABC 0 ABC 0 ABC 0 ABC 0
或
由于约束项的值始终为 0，所以既可以将约束 项写进逻辑函数式，也 可以不写。
ABC ABC ABC ABC ABC 0
逻辑函数中的无关项
BC A 0 1
1
00
01
1 1
11
1
10
1 1
卡诺图化简法
• 利用卡诺图化简函数
– 例1：用卡诺图化简 Y AC AC BC BC
Y AC AC BC BC AC BC AB
BC A 0 1
1
00
01
1 1
11
1
10
1 1
注：卡诺图化简不是唯 一，不同的圈法得到的 简化结果不同，但实现 的逻辑功能相同的。
0
11
0
10
0
最简或与式：
Y B( A C D)( A C D)
1
0 0
1
1 0
0
1 0
1
1 0
卡诺图化简法
• 利用卡诺图化简函数
– 例3：用卡诺图化简为最简与或式和最简或与式 Y M (2,3,4,6,11,12,14)

∑ ( 0 , 2 ,5,6 ,7 ,8,9 ,10 ,11,14 ,15 )
AB D
01 11 10
B C
AB BD
F = A BD + B D + A B + BC
3.3 卡诺图化简
F = ABD + B D + AB + BC
B D
A B A B D B C
& &
≥1
F
&
&
3.3 卡诺图化简
3.3 卡诺图化简
由一般式获得最小项标准式 代数法： 代数法：对逻辑函数采用拆项法
F = AB C + BC + AC = AB C + BC ( A + A) + AC ( B + B)
= AB C + ABC + ABC + ABC + ABC
真值表法：逻辑函数是真值表中 真值表法：逻辑函数是真值表中F=1那 那 些最小项相或而成的。 些最小项相或而成的。
3.3 卡诺图化简
ABC
000 001 010 011 100 101 110 111
AB C
1 0 0 0 0 0 0 0
BC
0 0 0 1 0 0 0 1
AC
0 0 0 0 1 0 1 0
F
1 0 0 1 1 0 1 1
AB C
ABC AB C ABC
ABC
F = AB C + ABC + AB C + ABC + ABC
3.3 卡诺图化简
最小项编号
序号 0 1 2 3 4 5 6 7 ABC 000 001 010 011 100 101 110 111 最小项名称

对于包含多个非门或多个连续的与或 非门的逻辑表达式，卡诺图化简可能 无法得到最简结果。
卡诺图对于大规模逻辑电路的优化效果有限
随着逻辑电路规模的增大，卡诺图的化简过程变得复杂且耗时，难以在实际工程 中应用。
对于大规模逻辑电路，可能需要采用其他优化方法，如布尔代数、门级优化等， 以获得更好的优化效果。
THANKS
感谢观看
卡诺图化简逻辑表达式
• 卡诺图简介 • 卡诺图化简逻辑表达式的方法 • 卡诺图化简逻辑表达式的实例 • 卡诺图与其他化简方法的比较 • 卡诺图的局限性
01
卡诺图简介
卡诺图的定义
• 定义：卡诺图是一种用于表示二进制逻辑函数关系的图形表示 法，通过将逻辑函数输入变量的所有可能取值组合在网格中表 示出来，可以直观地观察到函数的最简形式。
卡诺图与布尔代数化简的比较
布尔代数化简
通过使用逻辑运算（与、或、非）的代数性质，如吸收律、分配律等，对逻辑表达式进 行简化。这种方法需要一定的数学基础，但在处理复杂逻辑表达式时可能较为繁琐。
卡诺图化简
利用图形直观地表示输入变量的所有可能组合，通过排除法简化逻辑表达式。卡诺图化 简简单易懂，不需要复杂的数学运算，特别适合初学者和解决多变量逻辑表达式的化简
问题。
卡诺图与公式化简的比较
公式化简
通过逻辑运算的公式和定理，对逻辑表达式 进行简化。这种方法需要熟练掌握各种逻辑 公式和定理，对于初学者有一定的难度。
卡诺图化简
利用图形化的方式表示输入变量的所有可能 组合，通过排除法简化逻辑表达式。卡诺图 化简直观、易于操作，不需要复杂的公式和 定理，特别适合初学者和解决多变量逻辑表 达式的化简问题。
05
卡诺图的局限性
卡诺图适用范围有限

数，将应为“1”
的项填到卡诺图中
表2.6.7 Y的卡诺图
例2.6.7 用卡诺图表示下面 的逻辑函数
CD AB 00 01 11 10
Y A' B'C' D A' BD' ACD AB'
00
1
A 01 1
1
解：其卡诺图如表 2.6.7所示
11
1
A
10 1 1 1 1
2.6.2 卡诺图化简法
从上面卡诺图可以看出
任意两个相邻的最小项 在图上是相邻的，并且图中 最左列的最小项与左右列相 应最小项也是相邻的（如m0 和m2， m9和m10 )。位于最上 面和最下面的相应最小项也 是相邻的（ m0和m9 , m2和 m10)，所以四变量的最小项 有四个相邻最小项。可以证 明n变量的卡诺图中的最小项 有n个相邻最小项
Y ( A, B,C) A AC BC ABC 解: Y的卡诺图如表2.6.9所示
表2.6.9 Y的卡诺图
BC
A 00 01 11 10
1
011 11
111 11
2.6.2 卡诺图化简法 练习：画出下列函数的卡诺图
Y1 AB B BCD
Y2 ( A, B,C, D) m(0,1,2,3,4,6,7,8,9,11,15)
2.6.2 卡诺图化简法 下面表2.6.1 是二变量的卡诺图
表2.5.10 二变量
十进 制数
A
B
mi
0 0 0 AB(m0)
1 0 1 AB(m1) 2 1 0 AB(m2 )
3 1 1 AB(m3)
表2.6.1 二变量的卡诺图
B A0
1
0 m0
m1
1 m2 m3

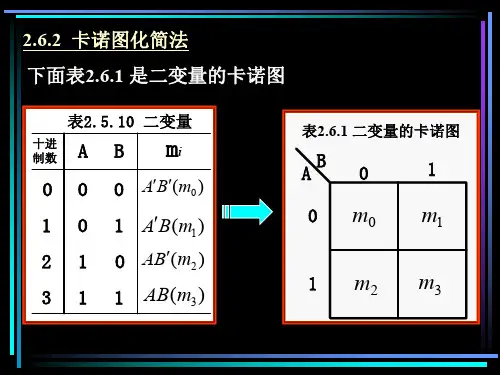
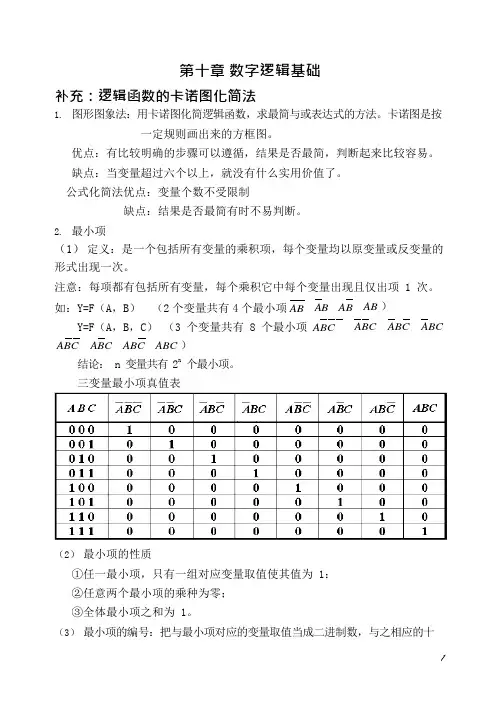
第十章数字逻辑基础补充：逻辑函数的卡诺图化简法1.图形图象法：用卡诺图化简逻辑函数，求最简与或表达式的方法。

卡诺图是按一定规则画出来的方框图。

优点：有比较明确的步骤可以遵循，结果是否最简，判断起来比较容易。

缺点：当变量超过六个以上，就没有什么实用价值了。

公式化简法优点：变量个数不受限制缺点：结果是否最简有时不易判断。

2.最小项（1）定义：是一个包括所有变量的乘积项，每个变量均以原变量或反变量的形式出现一次。

注意：每项都有包括所有变量，每个乘积它中每个变量出现且仅出项 1 次。

如：Y=F（A，B）（2 个变量共有4 个最小项AB AB AB AB ）Y=F（A，B，C）（3 个变量共有 8 个最小项ABC ABC ABC ABC ABC ABC ABC ABC ）结论： n 变量共有 2n个最小项。

三变量最小项真值表（2）最小项的性质①任一最小项，只有一组对应变量取值使其值为 1：②任意两个最小项的乘种为零；③全体最小项之和为 1。

（3）最小项的编号：把与最小项对应的变量取值当成二进制数，与之相应的十进制数，就是该最小项的编号，用 mi表示。

3.最小项表达式——标准与或式任何逻辑函数都可以表示为最小项之和的形式——标准与或式。

而且这种形式是惟一的，即一个逻辑函数只有一种最小项表达式。

例 1．写出下列函数的标准与或式：Y=F(A,B,C)=AB+BC+CA解：Y=AB( C +C)+BC( A +A)+CA( B +B)= ABC +ABC +ABC +ABC +ABC +ABC= ABC +ABC +ABC +ABC= m7 +m6+m5+m3例 2.写出下列函数的标准与或式：Y =AB +AD +BC解：Y =（A +B)( A +D)(B +C)= ( A +BD)(B +C)=AB +AB +AC +BCD=ABC +ABC +ABC +ABCD +ABCD=ABCD + _ ABCD +ABCD +ABCD +ABCD +ABCD +ABCD=m7 +m6+m5+m4+m1+m+m8＝∑m(0,1,4,5,6,7,8）列真值表写最小项表达式。

最后将全部积项逻辑加即得最简与或表达式 返 回
图形法化简函数
例：将F(A、B、C、D) ACD AB BCD ABC AC 化为最简与非—与非式 A B C BC 解： CD AB 00 01 11 化简得： 00 1 1 F AC BC AD BD ABC 01 1 1 BD 11 1 1 1 最简与非—与非式为： 10 1 1
例：将F(A、B、C、D) ACD AB BCD ABC AC 化为最简与非—与非式。 CD AB 00 01 11 10 解： ACD 00 1 1 0 m14,m15 0 01 1 0 1 两次填1 1 1 1 AB 11 1 1 10 B CD AC ABC 0 1
1
1
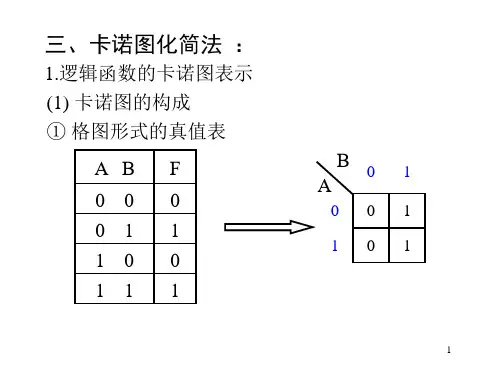
二、逻辑函数的卡诺图化简法
10
(b)
仔细观察可以发现，卡诺图实际上是按格雷码排列， 具有很强的相邻性：
3、卡诺图上的相邻项 （1）直观相邻性： 只要小方格在几何位置上（不管上下左右）相邻，它 代表的最小项在逻辑上一定是相邻的。
C
m
0
m
1
m
3
m
2
（2）循环相邻性： 每行、列的两头相邻 （3）对称相邻性： 五变量卡诺图折叠相邻
10
1
1
1
F F AC BC AD BD ABC
AC BC AD BD ABC
AD
AC
图形法化简函数
例：图中给出输入变量A、B、C的真值表，填写函数的卡 诺图 BC A B C F A 00 01 11 10 0 0 0 1 1 AB 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 1 1 1 1 0 0 1 ABC 1 0 1 0 得： 1 1 0 0 F= ABC + AB 1 1 1 0

例3.5.1：用卡诺图表示逻辑函数 F A, B, C BC 解：
F A, B, C BC A A BC ABC ABC m2 m6
A BC 0 1 00 0 0 01 0 0 11 0 0 10 1 1


方法二：将逻辑式表示成与或式，与项代表的最小项 在卡诺图中出现在行变量与列变量的交叉位置。在与项中 未出现的变量既以原变量形式出现，也以反变量形式出现。
2345任何n个变量的卡诺图是一块矩形区域该区域被划分为2个小方格每个小方格代表一个最小项所有最小项按一定顺序排列使几何相邻的最小项在逻辑上也相邻
3.5 逻辑函数的卡诺图化简法
3.5.1 最小项与最大项
1. 最小项与最大项的定义 最小项：n个变量的最小项是这n个变量的逻辑乘，每 个变量以原变量或反变量的形式出现且只出现一次。


ABC ABC ABC m7 m6 m0 m 0,6,7
或与标准型：任何一个逻辑式都可以表示成若干个最大项 积的形式。 F A, B, C m 0,6,7
m1 m2 m3 m4 m5 m1 m2 m3 m4 m5 M1M 2 M3M 4 M5 M 1,2,3,4,5
最大项：n个变量的最大项是这n个变量的逻辑和，每 个变量以原变量或反变量的形式出现且只出现一次。
三变量最小项和最大项的表示方法
2. 最小项和最大项的性质 (1) 给定n个变量的一组取值，这n个变量的2n个最小项中只 有一个等于1，2n个最大项中只有一个等于0。
(2) 全部最小项之和恒等于1；全部最大项之积恒等于0。 (4) 若干个最小项的和等于其余最小项和的反。
m2 m6
m18

总结词
卡诺图化简的基本步骤
详细描述
详细阐述卡诺图化简的基本步骤， 包括如何根据逻辑函数绘制卡诺图 、如何根据卡诺图进行化简等。
实例二：复杂的逻辑函数化简
总结词
通过卡诺图化简复杂逻辑函数
01
02
详细描述
选取具有代表性的复杂逻辑函数，如含有多 个变量和复合逻辑运算的函数，利用卡诺图 进行化简，展示化简过程和结果。
优化最小项的排列方式
优化最小项的排列方式，可以减少重复计算和提高化简效率。
THANKS
感谢观看
杂。
约束条件
卡诺图化简法要求逻辑函数在最小 项上的取值必须明确（0或1），对 于含有未知取值的逻辑函数不适用 。
非二进制系统
卡诺图仅适用于二进制逻辑系统， 对于非二进制系统（如三进制、四 进制等）需要其他化简方法。
03
卡诺图化简法的步骤
构造卡诺图
01
02
03
确定变量
首先确定待化简的逻辑函 数的变量，即确定卡诺图 的行数和列数。
注意约束条件
在使用卡诺图化简法时，应考虑约束条件，如输 入变量的取值范围和输出变量的取值范围。
避免重复计算
在化简过程中，应避免重复计算最小项，以提高 化简效率。
如何提高卡诺图化简法的效率
熟悉卡诺图化简法的步骤
熟练掌握卡诺图化简法的步骤，可以更快地完成化简过程。
选择合适的软件工具
使用合适的软件工具，如逻辑模拟软件等，可以提高卡诺图化简法 的效率。
《卡诺图化简法》 PPT课件
目录
• 卡诺图化简法简介 • 卡诺图的构成与特性 • 卡诺图化简法的步骤 • 卡诺图化简法的实例分析 • 卡诺图与其他化简方法的比较 • 卡诺图化简法的实际应用与注意事项

AB C ABC ABC
Y ( A, B, C ) m3 m6 m7 或： m (3,6,7)
2019/3/18
8
例2: 写出三变量函数的最小项表达式。 解 利用摩根定律将函数变换为与或表达 式，然后展开成最小项之和形式。
Y ( A, B, C ) AB AB C AB
2019/3/18 22
m3
BCD
m11
图1-15
2019/3/18
两个最小项合并
23
图1-16
2019/3/18
四个最小项合并
24
2019/3/18
图1-17
八个最小项合并
25
（2）利用卡诺图化简逻辑函数 A．基本步骤： ① 画出逻辑函数的卡诺图； ② 合并相邻最小项（圈组）； ③ 从圈组写出最简与或表达式。 关键是能否正确圈组 。 B．正确圈组的原则 ① 必须按2、4、8、2N的规律来圈取值为1的相 邻最小项； ② 每个取值为1的相邻最小项至少必须圈一次， 但可以圈多次； ③ 圈的个数要最少（与项就少），并要尽可能 大（消去的变量就越多）。
2019/3/18
卡诺图化简法
含有无关项的逻辑函数的化简
2
2.4 逻辑函数的卡诺图化简法
公式化简法评价： 优点：变量个数不受限制。 缺点：目前尚无一套完整的方法，结果是否最简 有时不易判断。
利用卡诺图可以直观而方便地化简逻辑函数。 它克服了公式化简法对最终化简结果难以确定等缺 点。 卡诺图是按一定规则画出来的方框图，是逻辑 函数的图解化简法，同时它也是表示逻辑函数的一 种方法。 卡诺图的基本组成单元是最小项，所以先讨论 2019/3/18 3 一下最小项及最小项表达式。
2019/3/18 26

CD AB 00 01 11 10
00 0
2
01 4 5 7 6
11 12 13 15 14
10 8
10
C
B
D
总结： 2n 个相邻最小项合并可以消去 n 个取值不同因子。
2. 用卡诺图化简逻辑函数的基本步骤
（1）首先将逻辑函数变换为最小项之和表达式。 （2）画出逻辑函数的卡诺图。 （3）将卡诺图中按照矩形排列的相邻1画圈为若干个相邻组。 （4）合并最小项。 （5）将合并后的乘积项加起来就是最简与或表达式。
② 约束项： 不会出现的变量取值所对应的最小项。 ③ 约束条件： 由约束项相加所构成的值为 0 的逻辑表达式。
例如，上例中 ABC 的不可能取值为 000 011 101 110 111
约束项： ABC ABC ABC ABC ABC
约束条件：A B C ABC ABC ABC ABC 0
01 1
11
11
10 1
11
Y A B AC A C D B D
[例4] 用卡诺图法求反函数的最简与或表达式
Y AB BC AC
[解] ① 画函数的卡诺图
② 合并函数值为 0 的最小项
③ 写出 Y 的反函数的 最简与或表达式
BC A 00 01 11 10
00 010
10 111
Y AB BC AC
（3）化简举例 [例] 化简逻辑函数
F(A,B,C,D )
m( 1 , 7 , 8 ) d( 3 , 5 , 9 , 10 , 12 , 14 , 15 )
[解] 化简步骤:
① 画函数的卡诺图，顺序 为：先填 1 ╳ 0
② 合并最小项，画圈时 ╳ 既可以当 1 ，又可以当 0

(4)再次，找只能按一条路径合并的八个相邻方格画圈
(5)依此类推，若还有1方格未被圈，找合适的圈画出
11
3、举例 单击此处编辑母版标题样式
5.1 应用卡诺图化简
• • • • •
单击此处编辑母版文本样式 第二级A BC 00 01 11 10 第三级 0 1 1 1 0 第四级 第五级 1 1 0 0 0
10 AB 00 01 11 10
1 1 1
0
0
1
0
0 0
1 1
0
1
0
1
0
Y2 ABCD AC D BC AB
13
例3：化简 单击此处编辑母版标题样式
5.1 应用卡诺图化简
• 单击此处编辑母版文本样式 第一步：
• • • • 第二级 00 AB 第三级 00 0 第四级 01 0 第五级
7
单击此处编辑母版标题样式
• 单击此处编辑母版文本样式 CD BC 00 •A 第二级 00 01 11 10 AB m0 00 0 A B C ABC ABC ABC • 第三级 01 m4 1 ABC ABC ABC ABC • 第四级 11 m12 • 第五级 10 m8
三变量卡诺图 四变量卡诺图
Y1 BC AC
例1：化简 Y1 ABC ABC ABC ABC
12
例2：化简 单击此处编辑母版标题样式
CD
5.1 应用卡诺图化简
Y2 m(0,3,4,5,12,13,14,15) • 单击此处编辑母版文本样式
• • • • 第二级 00 第三级 第四级 01 第五级 11
在卡诺图中，几何位置相邻（包括边缘、 四角）的小方格在逻辑上也是相邻的