卡诺图化简法
- 格式:ppt
- 大小:578.00 KB
- 文档页数:19





卡诺图化简法卡诺图化简法又称为图形化简法。
该方法简单、直观、容易掌握,因而在逻辑设计中得到广泛应用。
一卡诺图的构成卡诺图是一种平面方格图,每个小方格代表一个最小项,故又称为最小项方格图。
1.结构特点卡诺图中最小项的排列方案不是唯一的,图2.5(a)、(b)、(c)、(d)分别为2变量、3变量、4变量、5变量卡诺图的一种排列方案。
图中,变量的坐标值应0表示相变量的反变量,1表示相应变量的原变量。
各小方格依变量顺序取坐标值,所得二进制数对应的十进制数即相应最小项的下标i。
在五变量卡诺图中,为了方便省略了符号“m”,直接标出m的下标i。
图2. 5 2~5变量卡诺图从图2.5所示的各卡诺图可以看出,卡诺图上变量的排列规律使最小项的相邻关系能在图形上清晰地反映出来。
具体地说,在n个变量的卡诺图中,能从图形上直观、方便地找到每个最小项的n个相邻最小项。
以四变量卡诺图为例,图中每个最小项应有4个相邻最小项,如m5的4个相邻最小项分别是m1,m4,m7,m13,这4个最小项对应的小方格与m5对应的小方格分别相连,也就是说在几何位置上是相邻的,这种相邻称为几何相邻。
而m2则不完全相同,它的4个相邻最小项除了与之几何相邻的m3和m6之外,另外两个是处在“相对”位置的m0(同一列的两端)和m10(同一行的两端)。
这种相邻似乎不太直观,但只要把这个图的上、下边缘连接,卷成圆筒状,便可看出m0和m2在几何位置上是相邻的。
同样,把图的左、右边缘连接,便可使m2和m10相邻。
通常把这种相邻称为相对相邻。
除此之外,还有“相重”位置的最小项相邻,如五变量卡诺图中的m3,除了几何相邻的m1,m2,m7和相对相邻的m11外,还与m19相邻。
对于这种情形,可以把卡诺图左边的矩形重叠到右边矩形之上来看,凡上下重叠的最小项相邻,这种相邻称为重叠相邻。
归纳起来,卡诺图在构造上具有以下两个特点:☆ n个变量的卡诺图由2n个小方格组成,每个小方格代表一个最小项;☆ 卡诺图上处在相邻、相对、相重位置的小方格所代表的最小项为相邻最小项。



卡诺图化简法教案设计理念卡诺图化简法是一种用于逻辑设计和布尔代数化简的方法。
它通过图形化表示布尔函数的真值表,并利用布尔代数的基本规则来简化函数,从而减少逻辑电路的延迟和复杂度。
本教案设计旨在通过生动的实例和互动式的学习活动,帮助学生深入理解和掌握卡诺图化简法,并培养学生的分析和推理能力。
一、教学目标1. 理解布尔代数和布尔函数的基本概念;2. 掌握卡诺图的绘制方法和化简规则;3. 能够通过卡诺图化简法简化逻辑电路;4. 培养学生的逻辑思维和问题解决能力。
二、教学内容及方法1. 布尔代数和布尔函数的基本概念- 介绍布尔代数的概念和符号表示;- 解释布尔函数的定义和真值表表示。
2. 卡诺图的绘制方法和化简规则- 分步介绍卡诺图的绘制方法,重点讲解4变量和3变量卡诺图的绘制规则;- 讲解卡诺图的化简规则,包括最小项和最小项组合;- 通过实例和示意图演示化简过程。
3. 卡诺图化简法的应用- 通过布尔函数化简实例的讲解,引导学生掌握卡诺图化简法的具体操作步骤;- 引导学生分析和推理实例中的问题,培养学生的思维能力。
4. 教学方法- 演示法:通过示意图和实例演示卡诺图化简过程,帮助学生理解和掌握方法;- 讨论法:引导学生分组进行小组讨论,共同解决问题,提高学生的合作和交流能力;- 实践法:设计实际电路的布尔函数化简问题,让学生实际操作卡诺图进行化简。
三、教学过程安排1. 导入环节(10分钟)- 调动学生的学习兴趣,以符合基于实例的学习方法;- 引入布尔代数和布尔函数的概念,通过实例解释和示意图展示。
2. 知识教授(15分钟)- 分步介绍卡诺图的绘制方法,通过示例演示;- 讲解卡诺图化简规则,通过实例演示化简过程。
3. 学生实践(15分钟)- 分组讨论实例,学生自行尝试绘制卡诺图并进行化简;- 教师辅导和指导学生解决问题。
4. 深入拓展(20分钟)- 针对高年级学生,引入多变量卡诺图的绘制和化简方法;- 通过复杂实例演示,培养学生的推理和分析能力。


逻辑函数的卡诺图化简法代数化简法的优点是不受变量数目的限制。
缺点是:没有固定的步骤可循;需要熟练运用各种公式和定理;需要一定的技巧和经验;有时很难判定化简结果是否最简。
本节介绍一种比代数法更简便、直观的化简逻辑函数的方法。
它是一种图形法,是由美国工程师卡诺(Karnaugh )发明的,所以称为卡诺图化简法。
卡诺图实际上是真值表的一种变形,一个逻辑函数的真值表有多少行,卡诺图就有多少个小方格。
所不同的是真值表中的最小项是按照二进制加法规律排列的,而卡诺图中的每一项则是按照相邻性排列的。
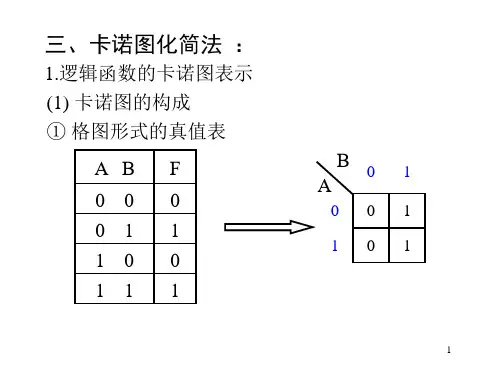
1.卡诺图的结构(1)二变量卡诺图。
00011110m ABm AB1m 03m AB AB4A(a)B 0132AB(b)(2)三变量卡诺图。
0m ABC m ABC 1m 3m ABC ABC 265m ABC74ABCm m m ABCABC0(a)(b)132457610011100BCA 01BC A(3)四变量卡诺图。
m 0ABCD ABCD m 1ABCD m 3m ABCD 2m 567m m ABCD ABCD m ABCD 4ABCD ABCD m m 13ABCD ABCD 1412m 15m ABCDABCD ABCD m ABCD 8m 1011m 9m ABCD ABCD 0132765413141512981110AB CD0000010111111010(a)(b)2.从真值表到卡诺图例3.2.3 某逻辑函数的真值表如表3.2.3所示,用卡诺图表示该逻辑函数。
解: 该函数为三变量,先画出三变量卡诺图,然后根据表3.2.3将8个最小项L 的取值0或者1填入卡诺图中对应的8个小方格中即可,如图3.2.4所示。
图3.2.4 例3.2.3的卡诺图3.从逻辑表达式到卡诺图(1)如果逻辑表达式为最小项表达式,则只要将函数式中出现的最小项在卡诺图对应的小方格中填入1,没出现的最小项则在卡诺图对应的小方格中填入0。