数字信号处理 上机实验

数字信号处理实验信息252120502123赵梦然实验一快速傅里叶变换与信号频谱分析一．实验目的1. 在理论学习的基础上，通过本实验加深对离散傅里叶变换的理解。

2. 熟悉并掌握按时间抽取编写快速傅里叶变换（FFT）算法的程序。

3. 了解应用FFT 进行信号频谱分析过程中可能出现的问题，例如频谱混淆、泄漏、栅栏效应等，以便在实际中正确使用FFT 算法进行信号处理。

二．实验内容1. 仔细分析教材第六章“时间抽取法FFT 的FORTRAN 程序”，编写出相应的使用FFT 进行信号频谱分析的Matlab 程序。

2. 用FFT 程序分析正弦信号，分别在以下情况进行分析，并讨论所得的结果：a) 信号频率F＝50Hz，采样点数N=32，采样间隔T=0.000625s；b) 信号频率F＝50Hz，采样点数N=32，采样间隔T=0.005s；c) 信号频率F＝50Hz，采样点数N=32，采样间隔T=0.0046875s；d) 信号频率F＝50Hz，采样点数N=32，采样间隔T=0.004s；e) 信号频率F＝50Hz，采样点数N=64，采样间隔T=0.000625s；f) 信号频率F＝250Hz，采样点数N=32，采样间隔T=0.005s；g) 将c)中信号后补32 个0，做64 点FFT，并与直接采样64 个点做FFT 的结果进行对比。

3. 思考题：1) 在实验a)、b)、c)和d)中，正弦信号的初始相位对频谱图中的幅度特性是否有影响？为什么？信号补零后做FFT 是否可以提高信号频谱的分辨率？为什么？三．实验程序function pushbutton1_Callback(hObject, eventdata, handles)F=str2double(get(handles.f,'string'));N=str2double(get(handles.n,'string'));T=str2double(get(handles.t,'string'));fai=str2double(get(handles.fai,'string'));zero=get(handles.zero,'value');%进行采样t=0:T:(N-1)*T;x=cos(2*pi*F*t+fai);%进行fft运算if zeroy=abs(fft(x,N+32));y=y/max(y);elsey=abs(fft(x));y=y/max(y);end%画图axes(handles.axes2);stem((0:N-1),x,'*');axes(handles.axes1);if zerostem((0:N+31),y,'.');elsestem((0:N-1),y);endxlabel('频率/Hz');ylabel('振幅');grid on;四．实验结果实验数据记录：（a）输入信号频率：50输入采样点数：32输入间隔时间：0.000625是否增加零点？否信号频率F=50Hz，采样长N=32，采样周期T=0.000625s，fs=1/T=1600Hz，基频为fs/N=50Hz，50/50=1.故此在频谱图上的第1个点和第31个点有值。

《数字信号处理》上机实验指导《数字信号处理》上机实验指导实验一、Z 变换及离散时间系统分析（一）、实验目的1、通过本实验熟悉Z 变换在离散时间系统分析中的地位和作用。

2、掌握并熟练使用有关离散系统分析的MATLAB 调用函数及格式，以深入理解离散时间系统的频率特性。

（二）、实验内容及步骤对于一个给定的LSI 系统，其转移函数H(z)习惯被定义为H(z)=B(z)/A(z),即：abn a n b z n a z a z a z n b z b z b A B H ------++++++++++==)1(...)3()2(1)1(...)3()2()1(b )z ()z ()z (2121 公式中b n 和an 分别是H(Z)分子与分母多项式的阶次，在有关MATLAB 的系统分析的文件中，分子和分母的系数被定义为向量，即)]1(),...,2(),1([)]1(),...,2(),1([+=+=a b n a a a a n b b b b并要求)1(a =1,如果)1(a ≠1，则程序将自动的将其归一化为1。

1、系统的阶跃响应调用格式为：y=filter(b,a,x),其中x,y,a,b 都是向量。

例1 令4321432155075.02925.28291.30544.31001836.0007374.0011 016.0007344.0001836.0)z (--------+-+-++++=z z z z z z z z H 求该系统的阶跃响应（y （n ））。

实现该任务的程序如下：clear;x=ones(100);% x(n)=1,n=1~100；t=1:100;% t 用于后面的绘图；b=[.001836，.007344，.011016，.007374，.001836]; % 形成向量b ；a=[1，-3.0544，3.8291，-2.2925，.55075]; % 形成向量a ；y=filter(b,a,x);% 求所给系统的输出，本例实际上是求所给系统的阶跃响应；plot(t,x,'r.',t,y,'k-');grid on;% 将x(n)（绿色）y(n)（黑色）画在同一个%图上；ylabel('x(n) and y(n)')xlabel('n')2、单位抽样响应h(n)调用格式为：h=impz(b ，a ，N) 或 [h ，t]=impz(b ，a ，N)其中N 是所需的h(n)的长度，前者绘图时n 从1开始，而后者从0开始。

数字信号处理上机实验报告实验一 熟悉MATLAB 环境一、实验目的1、 熟悉MATLAB 的主要操作命令。

2、 学会简单的矩阵输入和数据读写。

3、 掌握简单的绘图命令。

4、 用MATLAB 编程并学会创建函数。

5、 观察离散系统的频率响应。

二、实验内容认真阅读本章附录，在MATLAB 环境下重新做一遍附录中的例子，体会各条命令的含义。

在熟悉MATLAB 基本命令的基础上，完成以下实验。

上机实验内容：1、 数组的加减乘除和乘方运算，输入[]4 3 2 1=A ，[]6 5 4 3=B ，求B A C +=，B A D -=，B A E *=.，B A F /.=，B A G .^=，并用stem 语句画出A 、B 、C 、D 、E 、F 、G 。

程序：>> A=[1 2 3 4];B=[3 4 5 6];C=A+B; D=A-B; E=A.*B; F=A./B; G=A.^B;subplot(2,4,1);stem(A,'.'); subplot(2,4,2);stem(B,'.'); subplot(2,4,3);stem(C,'.'); subplot(2,4,4);stem(D,'.'); subplot(2,4,5);stem(E,'.'); subplot(2,4,6);stem(F,'.');subplot(2,4,7);stem(G,'.')2、 用MATLAB 实现下列序列。

a) 150 8.0)(≤≤=n n x nb) 150 )()32.0(≤≤=+n en x n jc) 150 )1.025.0sin(2)2.0125.0cos(3)(≤≤+++=n n n n x ππππ 程序： A) clear;clc; n=[0:15]; x1=0.8.^n;subplot(3,1,1),stem(x1) title('x1=0.8^n')xlabel('n'); ylabel('x1');B)clear;clc;n=[0:15];x2=exp((0.2+3j)*n);subplot(3,1,1),stem(x2)title('x2=exp((0.2+3j)*n)')xlabel('n'); ylabel('x2');C)clear;clc;n=[0:15];x3=3*cos(0.125*pi*n+0.2*pi)+2*sin(0.25*pi*n+0.1*pi);subplot(3,1,1),stem(x3)title('x3=3*cos(0.125*pi*n+0.2*pi)+2*sin(0.25*pi*n+0.1*pi)') xlabel('n'); ylabel('x3');3、 绘出下列时间常数的图形，对x 轴，y 轴以及图形上方均须加上适当的标注： a) s t t t x 100 )2sin()(≤≤=π b) 4s t 0 )sin()100cos()(≤≤=t t t x ππ >> m=0:0.01:10; n=0:0.01:4; x1t=sin(2*pi*m);x2t=cos(100*pi*n).*sin(pi*n); subplot(2,1,1);plot(m,x1t); subplot(2,1,2);plot(n,x2t);4、 给定一因果系统H(z)=(1+2-1-z z 2+)/(2167.0-1--+z z )，求出并绘制H(z)的幅频响应与相频响应。

数字信号处理上机实验及参考程序数字信号处理实验实验⼀离散时间信号与系统及MA TLAB实现1.单位冲激信号：n = -5:5;x = (n==0);subplot(122);stem(n, x);2.单位阶跃信号：x=zeros(1,11);n0=0;n1=-5;n2=5;n = n1:n2;x(:,n+6) = ((n-n0)>=0);stem(n,x);3.正弦序列：n = 0:1/3200:1/100;x=3*sin(200*pi*n+1.2);stem(n,x);4.指数序列n = 0:1/2:10;x1= 3*(0.7.^n);x2=3*exp((0.7+j*314)*n);subplot(221);stem(n,x1);subplot(222);stem(n,x2);5.信号延迟n=0:20;Y1=sin(100*n);Y2=sin(100*(n-3));subplot(221);stem(n,Y1);subplot(222);stem(n,Y2);6.信号相加X1=[2 0.5 0.9 1 0 0 0 0];X2=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];X=X1+X2;stem(X);7.信号翻转X1=[2 0.5 0.9 1];n=1:4;X2=X1(5-n);subplot(221);stem(n,X1);subplot(222);stem(n,X2);8.⽤MATLAB计算序列{-2 0 1 –1 3}和序列{1 2 0 -1}的离散卷积。

a=[-2 0 1 -1 3]; b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n');ylabel('幅度');9．⽤MA TLAB计算差分⽅程当输⼊序列为时的输出结果。

N=41;a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=filter(a,b,x);stem(k,y)xlabel('n');ylabel('幅度')10.冲激响应impzN=64;a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=impz(a,b,N);stem(k,y)xlabel('n');ylabel('幅度')11.传递函数频率响应a=[0.8 -0.44 0.36 0.22];%分⼦的系数数组b=[1 0.7 -0.45 -0.6];%分母的系数数组n=(0:500)*pi/500%在pi范围内取501个采样点[h,f]=freqz(a,b,n);%求系统的频率响应subplot(2,1,1),plot(n/pi,abs(h));grid%作系统的幅度频响图axis([0,1,1.1*min(abs(h)),1.1*max(abs(h))]);ylabel('幅度');subplot(2,1,2),plot(n/pi,angle(h));grid %作系统的相位频响图axis([0,1,1.1*min(angle(h)),1.1*max(angle(h))]);ylabel('相位');xlabel('以pi为单位的频率');12.系统零极点图a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];h=zplane(a,b);实验⼆离散信号变换1.解⽅程y(n)-2y(n-1)+3y(n-2)=4x(n)-5x(n-1)+6x(n-2)-7x(n-3)a=[4,-5,6,-7];b=[1,-2,3];n=[0:7]; x=ones(length(n));Y=[-1,1];X=[1,-1];xic=filtic(b,a,Y,X);y1=filter(b,a,x,xic)stem(n,y1);xlabel('n');ylabel('y(n)');2．对连续的单⼀频率周期信号按采样频率采样，截取长度N分别选N =20和N =16，观察其DFT结果的幅度谱。

本科实验报告实验名称：数字信号处理上机实验作业1：用DFT 分析周期序列的频谱任务：设周期序列()cos(0.48)cos(0.52)xn n n ππ=+ 截取 N 点长得到 ()()()N x n x n R n = （1）N=10，做10点DFT ，得到 X1(k);（2）N=10，做100点补零DFT ，得到 X2(k); （3）N=100，做100点DFT ，得到 X3(k)。

要求：针对以上三种情况，分别输出|X1(k)|、|X2(k)|、|X3(k)|的图形，并进行比较、分析和讨论。

程序：clear all ; n=0:1000;xn=cos(pi*0.48*n)+cos(pi*0.52*n); Xk1=fft(xn(1:10),10); X1=abs(Xk1); subplot(3,1,1); stem(X1,'.'); xlabel('k'); ylabel('|X1(k)|'); title('N=10,10点DFT'); Xk2=fft(xn(1:10),100); X2=abs(Xk2); subplot(3,1,2); stem(X2,'.'); xlabel('k'); ylabel('|X2(k)|');title('N=10,100点补零DFT'); Xk3=fft(xn(1:100),100); X3=abs(Xk3); subplot(3,1,3); stem(X3,'.'); xlabel('k'); ylabel('|X3(k)|'); title('N=100,100点DFT');运行结果：k|X 1(k )|N=10,10点DFTk|X 2(k )|N=10,100点补零DFTk|X 3(k )|N=100,100点DFT分析：从幅度谱中我们可以明显看出，X1(k)的相邻谱线间隔大，栅栏效应明显，频率分辨率低。

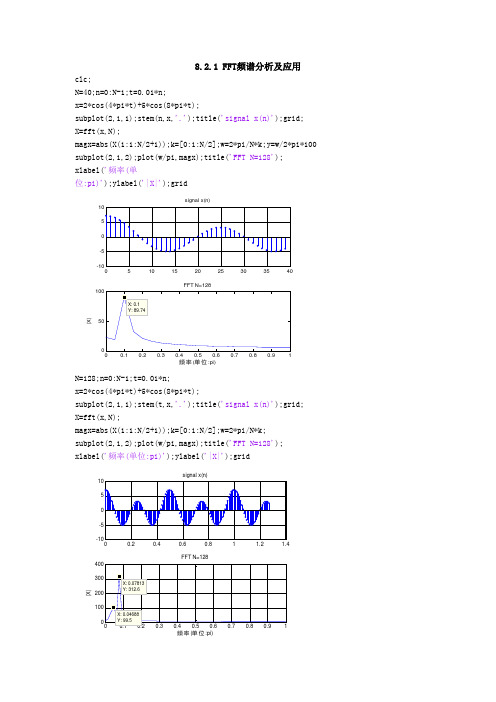
8.2.1 FFT 频谱分析及应用clc;N=40;n=0:N-1;t=0.01*n; x=2*cos(4*pi*t)+5*cos(8*pi*t);subplot(2,1,1);stem(n,x,'.');title('signal x(n)');grid; X=fft(x,N);magx=abs(X(1:1:N/2+1));k=[0:1:N/2];w=2*pi/N*k;y=w/2*pi*100 subplot(2,1,2);plot(w/pi,magx);title('FFT N=128'); xlabel('频率(单位:pi)');ylabel('|X|');grid510152025303540-10-50510signal x(n)00.10.20.30.40.50.60.70.80.9150100X: 0.1Y: 89.74FFT N=128频率(单位:pi)|X |N=128;n=0:N-1;t=0.01*n; x=2*cos(4*pi*t)+5*cos(8*pi*t);subplot(2,1,1);stem(t,x,'.');title('signal x(n)');grid; X=fft(x,N);magx=abs(X(1:1:N/2+1));k=[0:1:N/2];w=2*pi/N*k; subplot(2,1,2);plot(w/pi,magx);title('FFT N=128'); xlabel('频率(单位:pi)');ylabel('|X|');grid0.20.40.60.811.21.4-10-50510signal x(n)00.10.20.30.40.50.60.70.80.91100200300400X: 0.07813Y: 312.6X: 0.04688Y: 99.5FFT N=128频率(单位:pi)|X |t=0:0.001:0.3;x=sin(2*pi*50*t)+sin(2*pi*120*t);subplot(2,1,1);stem(t,x,'.');title('signal x(n)');grid; y=x+1.5*randn(1,length(t)); fs=1000; N=512; Y=fft(y,N); P=Y.*conj(Y)/N;p=P(1:1:N/2+1);f=fs*(0:N/2)/N;subplot(2,1,2);plot(f,p);title('FFT N=512');grid; xlabel('频率（单位：Hz ）');ylabel('功率谱');grid;0.050.10.150.20.250.30.35-2-1012signal x(n)50100150200250300350400450500010203040X: 50.78Y: 33.18X: 121.1Y: 39.78FFT N=512频率（单位：Hz ）功率谱clc; fs=32000;s=wavread('s8.wav'); N=1024; S=fft(s,N);magx=abs(S(1:1:N/2+1));f=fs*(0:N/2)/N; plot(f,magx);title('FFT');02000400060008000100001200014000160002468101214X: 1375Y: 13.56X: 875Y: 2.314FFT8.2.2 IIR 数字滤波器clear;clc;close all ;Rp=1.2;Rs=20;T=0.001;fp=300;fs=200; wp=2*pi*fp*T;ws=2*pi*fs*T;wp1=(2/T)*tan(wp/2);ws1=(2/T)*tan(ws/2);[n,wn]=cheb1ord(wp1,ws1,Rp,Rs,'s');[b,a]=cheby1(n,Rp,wn,'high','s'); [bz,az]=bilinear(b,a,1/T) [db,mag,pha,grd,w]=freqz_m(bz,az); plot(w/pi,db);axis([0,1,-30,2]);grid;00.10.20.30.40.50.60.70.80.91-30-25-20-15-10-5X: 0.4Y: -21.71X: 0.6Y: -1.2X: 0.776Y: -1.2bz =0.0691 -0.2073 0.2073 -0.0691 az =1.0000 1.0327 0.9031 0.3174clear;clc;close all ; %脉冲响应不变法Rp=1;Rs=25;T=0.001;fp=200;fs=300; wp=2*pi*fp;ws=2*pi*fs;[n,wn]=buttord(wp,ws,Rp,Rs,'s'); [b,a]=butter(n,wn,'s'); [bz,az]=impinvar(b,a,1/T) [db,mag,pha,grd,w]=freqz_m(bz,az); plot(w/(2*pi*T),db,'Color','r');hold on %双线性变换法wp=2*pi*fp*T;ws=2*pi*fs*T;wp1=(2/T)*tan(wp/2);ws1=(2/T)*tan(ws/2);[n,wn]=buttord(wp1,ws1,Rp,Rs,'s'); [b,a]=butter(n,wn,'s'); [bz,az]=bilinear(b,a,1/T) [db,mag,pha,grd,w]=freqz_m(bz,az);plot(w/(2*pi*T),db);axis([0,500,-80,2]);grid;hold off050100150200250300350400450500-80-70-60-50-40-30-20-100X: 300Y: -25X: 200Y: -0.5977X: 200Y: -0.8396脉冲响应不变法bz =-0.0000 0.0002 0.0153 0.0995 0.1444 0.0611 0.0075 0.0002 0.0000 0 az =1.0000 -1.9199 2.5324 -2.2053 1.3868 -0.6309 0.2045 -0.0450 0.0060 -0.0004 双线性变换法bz =0.0179 0.1072 0.2681 0.3575 0.2681 0.1072 0.0179 az =1.0000 -0.6019 0.9130 -0.2989 0.1501 -0.0208 0.0025clear;clc;close all ;Rp=3;Rs=15;wp1=0.25*pi;wp2=0.45*pi;ws1=0.15*pi;ws2=0.55*pi;T=0.01; wp3=(2/T)*tan(wp1/2);wp4=(2/T)*tan(wp2/2); ws3=(2/T)*tan(ws1/2);ws4=(2/T)*tan(ws2/2); wp=[wp3,wp4];ws=[ws3,ws4]; [n,wn]=buttord(wp,ws,Rp,Rs,'s'); [z,p,k]=buttap(n); [b,a]=zp2tf(z,p,k); w0=sqrt(wp3*wp4);Bw=wp4-wp3; [b1,a1]=lp2bp(b,a,w0,Bw); [bz,az]=bilinear(b1,a1,1/T);[db,mag,pha,grd,w]=freqz_m(bz,az); plot(w/pi,db);axis([0,1,-50,2]);0.10.20.30.40.50.60.70.80.91-50-45-40-35-30-25-20-15-10-50X: 0.15Y: -26.88X: 0.25Y: -3.01X: 0.45Y: -3.01X: 0.55Y: -17.81bz =0.0181 -0.0000 -0.0543 -0.0000 0.0543 -0.0000 -0.0181 az =1.0000 -2.2722 3.5153 -3.2688 2.3131 -0.9629 0.27818.2.3 FIR 数字滤波器的设计clear;clc;close all ;Wp=0.3*pi;Ws=0.5*pi;Rp=0.25;Rs=50; Wc=(Ws+Wp)/2; N=15;n=[0:1:N-1]; hd=ideal_lp(Wc,N); w_han=(hamming(N))'; h=hd.*w_han;[db,mag,pha,grd,w]=freqz_m(h,1);subplot(2,1,1);plot(w/pi,db);axis([0,1,-130,5]);xlabel('w/pi');ylabel('dB');grid; subplot(2,1,2);plot(w/pi,pha);axis([0,1,-4,4]);xlabel('w/pi');ylabel('pha');grid;0.10.20.30.40.50.60.70.80.91-100-50w/pid BN=15X: 0.694Y: -48.1700.10.20.30.40.50.60.70.80.91-4-2024w/pip h aclear;clc;close all ;Wp=0.3*pi;Ws=0.5*pi;Rp=0.25;Rs=50; Wc=(Ws+Wp)/2; N=45;n=[0:1:N-1]; hd=ideal_lp(Wc,N); w_han=(hamming(N))'; h=hd.*w_han;[db,mag,pha,grd,w]=freqz_m(h,1);subplot(2,1,1);plot(w/pi,db);axis([0,1,-130,5]);xlabel('w/pi');ylabel('dB');grid; subplot(2,1,2);plot(w/pi,pha);axis([0,1,-4,4]);xlabel('w/pi');ylabel('pha');grid;0.10.20.30.40.50.60.70.80.91-100-50w/pid BN=45X: 0.492Y: -51.7900.10.20.30.40.50.60.70.80.91-4-2024w/pip h aclear;clc;close all ;Wp=0.3*pi;Ws=0.5*pi;Rp=0.25;Rs=50; Wc=(Ws+Wp)/2; N=45;n=[0:1:N-1]; hd=ideal_lp(Wc,N);w_han=(hanning(N))'; h=hd.*w_han;[db,mag,pha,grd,w]=freqz_m(h,1);plot(w/pi,db);axis([0,1,-130,10]);xlabel('w/pi');ylabel('dB');grid;title('N=45');ho ld on ;w_han=(blackman(N))'; h=hd.*w_han;[db,mag,pha,grd,w]=freqz_m(h,1); plot(w/pi,db,'Color','r');hold off ;0.10.20.30.40.50.60.70.80.91-120-100-80-60-40-20X: 0.486Y: -44.03w/pid BN=45X: 0.582Y: -75.29hanning blackmanclear;clc;close all ; N=33;wc=0.275*pi;alpha=(N-1)/2;k=0:N-1;wk=(2*pi/N)*k; Hk=[ones(1,5),0.5,zeros(1,22),0.5,ones(1,4)]; angH=-alpha*(2*pi)/N*k;H=Hk.*exp(i*angH); h=real(ifft(H,N));[db,mag,pha,grd,w]=freqz_m(h,1); [Hr,ww,a,L]=Hr_Type1(h); subplot(2,1,1);plot(ww/pi,Hr,wk(1:33)/pi,Hk(1:33),'o');title('time domain');axis([0,1,-0.5,1.2]);grid;subplot(2,1,2);plot(w/pi,db);title('frequency');axis([0,1,-100,5]);grid00.10.20.30.40.50.60.70.80.91-0.500.51time domain00.10.20.30.40.50.60.70.80.91-100-50frequencyX: 0.386Y: -30.07clear;clc;close all ; N=34;wc=0.275*pi;alpha=(N-1)/2;k=0:N-1;wk=(2*pi/N)*k;Hk=[ones(1,5),0.5925,0.1099,zeros(1,21),-0.1099,-0.5925,-ones(1,4)]; angH=-alpha*(2*pi)/N*k;H=Hk.*exp(i*angH); h=real(ifft(H,N));[db,mag,pha,grd,w]=freqz_m(h,1); [Hr,ww,a,L]=Hr_Type2(h);subplot(2,1,1);plot(ww/pi,Hr,wk(1:34)/pi,Hk(1:34),'o');title('time domain');axis([0,1,-0.5,1.2]);grid;subplot(2,1,2);plot(w/pi,db);title('frequency');axis([0,1,-100,5]);grid00.10.20.30.40.50.60.70.80.91-0.500.51time domain00.10.20.30.40.50.60.70.80.91-100-50frequencyX: 0.424Y: -61.42。

实验1 抽样定理的实验体会实验内容：把下述三个连续时间信号()x t 转换成离散时间信号()s x nT ，在计算机上绘出()s x nT 的图形。

1/s s f T =为抽样频率。

自行依次选取不同的抽样频率，如00000.5,,2,5s f f f f f =等。

（1） 工频信号：10()sin(2)x t A f t π=，220A =，050f Hz =Dt=0.00005;t=-0.005:Dt:0.05; A=220; fo=50;xa=A*sin(2*pi*fo*t); Ts=0.04;n=-25:1:25; x=A*sin(2*pi*fo*n*Ts); stem(n,x,'fill'); grid on ;图1.1 fs=25Hz 时()s x nT 的图形x nT的图形图1.2 fs=50Hz时()sx nT的图形图1.3 fs=100Hz时()s图1.3 fs=250Hz 时()s x nT 的图形（2） 衰减正弦信号：20()sin(2)t x t Ae f t απ-=，2A =，0.5α=，02f Hz =Dt=0.00005;t=-0.005:Dt:0.05; A=2;a=0.5;fo=2;xa=A*exp(-a*t).*sin(2*pi*fo*t); Ts=1;n=-25:1:25;x=A*exp(-a*n*Ts).*sin(2*pi*fo*n*Ts); stem(n,x,'fill'); grid on ;图2.1 fs=1Hz 时()s x nT 的图形x nT的图形图2.2 fs=2Hz时()sx nT的图形图2.3 fs=4Hz时()sx nT的图形图2.4 fs=10Hz时()s（3）谐波信号：3201()sin(2)iix t A f itπ==∑，11A=，20.5A=，30.2A=，5f Hz=Dt=0.00005;t=-0.005:Dt:0.05;A1=1;A2=0.5;A3=0.2;fo=5;xa=A1*sin(2*pi*fo*t)+A2*sin(2*pi*fo*2*t)+A3*sin(2*pi*pi*3*t);Ts=0.4;n=-25:1:25;x=A1*sin(2*pi*fo*n*Ts)+A2*sin(2*pi*fo*2*n*Ts)+A3*sin(2*pi*pi*3* n*Ts);stem(n,x,'fill');grid on;图3.1 fs=2.5Hz时()sx nT的图图3.2 fs=5Hz时()sx nT的图形x nT的图形图3.3 fs=10Hz时()sx nT的图形图3.4 fs=25Hz时()s实验2 离散信号的DTFT 和DFT实验内容： 分别计算16点序列 150,165cos )(≤≤=n n n x π的16点和32点DFT ，绘出幅度谱图形，并绘出该序列的DTFT 图形。

数字信号处理上机实验实验二 时域采样及频域采样一． 实验目的：时域采样理论与频域采样理论是数字型号的重要理论是数字信号处理中的重要理论，以及如何选择采样频域才能使采样后的信号不丢失信息；掌握频域采样会引起的时域周期性变化的概念，以及频域采样点数选择指导作用。

二．实验原理与方法：频域采样定理的要点是： ①对信号()n x 的频谱函数()jwe X 在[0,2π]上等间隔采样N 点，得到：()()N==k j NeX k Xπωω2 1,...2,1,0-=N k则N 点)]([k XIDFTN得到的序列就是原序列()n x 以N 为周期进行周期延拓后的主值区序列，公式为)]()([)]([)(n R iN n x k XIDFT n x N i NNN ∑∞-∞==+==②由上式可知，频域采样点数N 必须大于等于时域离散信号的长度M(即MN≥),才能使时域不产生混叠，则N 点)]([k XIDFTN得到的序列)(n x N 就是)(n x ，即)(n x N=)(n x 。

如果MN>，)(n x N比原序列尾部多M N -个零点；如果MN<，则)(n x N=)]([k XIDFTN发生了时域混叠失真，而且)(n x N 的长度N 也比)(n x 的长度M 短，因此，)(n x N与)(n x 不相同。

三、 实验内容及步骤：⑴⎪⎩⎪⎨⎧≤≤≤≤-+=其它26141300271)(n n nn n x依题意，使用MATLAB 及其函数库列写程序如下：xa=1:1:14; xb=13:-1:1; xn=[xa,xb];xk=fft(xn,1024); k=0:1023; wk=2*k/1024;x32k=xk(1,1:32:1024); x32n=ifft(x32k,32); x16k=x32k(1,1:2:32); x16n=ifft(x16k,16); figure(1);subplot(3,2,1); stem(0:26,xn,'.');title('三角波序列x(n)');xlabel('n');ylabel('x(n)'); subplot(3,2,2); plot(wk,abs(xk));title('FT[x(n)]');xlabel('\omega/pi');ylabel('|X(e^j^\omega)|');subplot(3,2,3);stem(0:31,x32n,'.');axis([0,31,0,15]);title('32点IDFT[X_3_2(n)]');xlabel('n');ylabel('x_3_2(n'); subplot(3,2,4);stem(0:31,abs(x32k),'.');axis([0,31,0,200]);title('32点频率采样');xlabel('k');ylabel('X_3_2(n)'); subplot(3,2,5);stem(0:15,x16n,'.');axis([0,16,0,15]);title('16点IDFT[X_1_6(n)]');xlabel('n');ylabel('x_1_6(n)'); subplot(3,2,6);stem(0:15,abs(x16k),'.');axis([0,16,0,200]);title('16点频域采样');xlabel('k');ylabel('X_1_6(n)');102030三角波序列x(n)nx (n )0.51 1.520100200FT[x(n)]ω/pi|X (e j ω)|32点IDFT[X 32(n)]nx 32(n32点频域采样kX 32(n )5101516点IDFT[X 16(n)]nx 16(n )16点频域采样kX 16(n )实验总结分析： 当采样点16=N,小于27，发生时域混叠失真，因此)(16n x 与)(n x 不相同。

第十章上机实验数字信号处理是一门理论和实际密切结合的课程，为深入掌握课程内容，最好在学习理论的同时，做习题和上机实验。

上机实验不仅可以帮助读者深入的理解和消化基本理论，而且能锻炼初学者的独立解决问题的能力。

本章在第二版的基础上编写了六个实验，前五个实验属基础理论实验，第六个属应用综合实验。

实验一系统响应及系统稳定性。

实验二时域采样与频域采样。

实验三用FFT对信号作频谱分析。

实验四IIR数字滤波器设计及软件实现。

实验五FIR数字滤波器设计与软件实现实验六应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度，安排学生上机进行实验。

建议自学的读者在学习完第一章后作实验一；在学习完第三、四章后作实验二和实验三；实验四IIR数字滤波器设计及软件实现在。

学习完第六章进行；实验五在学习完第七章后进行。

实验六综合实验在学习完第七章或者再后些进行；实验六为综合实验，在学习完本课程后再进行。

function?tstem(xn,yn)%时域序列绘图函数%?xn:信号数据序列，yn:绘图信号的纵坐标名称（字符串）n=0:length(xn)-1;stem(n,xn,'.');box?onxlabel('n');ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)])10.1 实验一: 系统响应及系统稳定性1.实验目的（1）掌握求系统响应的方法。

（2）掌握时域离散系统的时域特性。

（3）分析、观察及检验系统的稳定性。

2.实验原理与方法在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。

已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应，本实验仅在时域求解。

在计算机上适合用递推法求差分方程的解，最简单的方法是采用MATLAB语言的工具箱函数filter函数。

也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。