下载文档原格式
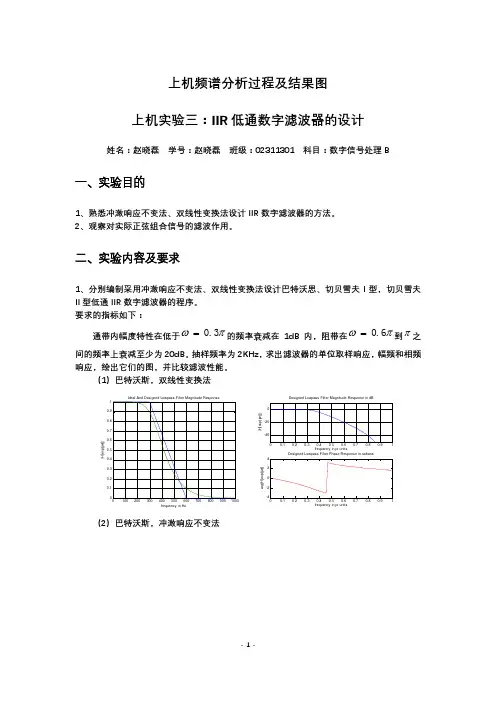
上机频谱分析过程及结果图 上机实验三：IIR 低通数字滤波器的设计姓名：赵晓磊 学号：赵晓磊 班级：02311301 科目：数字信号处理B一、实验目的1、熟悉冲激响应不变法、双线性变换法设计IIR 数字滤波器的方法。
2、观察对实际正弦组合信号的滤波作用。
二、实验内容及要求1、分别编制采用冲激响应不变法、双线性变换法设计巴特沃思、切贝雪夫I 型，切贝雪夫II 型低通IIR 数字滤波器的程序。
要求的指标如下：通带内幅度特性在低于πω3.0=的频率衰减在1dB 内，阻带在πω6.0=到π之间的频率上衰减至少为20dB 。
抽样频率为2KHz ，求出滤波器的单位取样响应，幅频和相频响应，绘出它们的图，并比较滤波性能。
（1）巴特沃斯，双线性变换法Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radians frequency in pi unitsa r g (H [e x p (j w )]（2）巴特沃斯，冲激响应不变法（3）切贝雪夫I 型，双线性变换法（4）切贝雪夫Ⅱ型，双线性变换法综合以上实验结果，可以看出，使用不同的模拟滤波器数字化方法时，滤波器的性能可能产生如下差异：使用冲击响应不变法时，使得数字滤波器的冲激响应完全模仿模拟滤波器的冲激响应，也就是时域逼急良好，而且模拟频率和数字频率之间呈线性关系；但频率响应有混叠效应。
frequency in Hz|H [e x p (j w )]|Designed Lowpass Filter Magnitude Response in dBfrequency in pi units|H [e x p (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [e xp (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radiansfrequency in pi unitsa r g (H [e x p (j w )]使用双线性变换法时，克服了多值映射的关系，避免了频率响应的混叠现象；在零频率附近，频率关系接近于线性关系，高频处有较大的非线性失真。
第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--，分别求它们的自相关函数，并证明二者都是偶对称的实序列。
解：111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时，122()1mmnx n ma r m aaa∞-===-∑ 当0m <时，122()1m mnx n a r m aaa -∞-===-∑ 所以，12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。
5.2 设()e()nTx n u n -=，T 为采样间隔。
求()x n 的自相关函数()x r m 。
解：解：()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+，其中12,,,A B f f 均为常数。
求()x n 的自相关函数()x r m 。
解：解：()x n 可表为)()()(n v n u n x +=的形式，其中)2sin()(11s nT f A n u π=，=)(n v 22sin(2)s A f nT π，)(),(n v n u 的周期分别为 s T f N 111=，sT f N 221=，()x n 的周期N 则是21,N N 的最小公倍数。
实验五 IIR滤波器设计一、实验目的1. 掌握冲激响应不变法和双线性变换法设计IIR数字滤波器的原理和方法；2. 观察双线性变换法和冲激响应不变法设计的滤波器的频域特性，了解双线性变换法和冲激响应不变法的特点和区别。
二、实验仪器1. 计算机2. MATLAB软件三、预习要求理解冲激响应不变法，双线性变换法，掌握常用 matlab 程序。
四、实验原理1. IIR数字滤波器一般为线性移不变的因果离散系统，N阶IIR滤波器的传递函数为：，式中系数至少有一个不为0。
IIR数字滤波器的设计通常利用模拟滤波器作为原型滤波器，直接由模拟滤波器的频率响经过冲激响应不变法或双线性变换法转换成IIR数字滤波器。
2. 常用模拟原型滤波器（1）巴特沃斯滤波器巴特沃斯滤波器通带和阻带都单调衰减，所有结束的幅度函数-3dB点为同一点。
其幅度响应为：，式中N为滤波器阶数，通带截止频率。
（2）切比雪夫Ⅰ型滤波器切比雪夫Ⅰ型滤波器在通带呈现等波纹特性，阻带单调衰减，其幅度响应为：，式中N为滤波器阶数；，表示通带波纹大小，越大，波纹越大；为截止频率，不一定为3dB带宽；为N阶Chebyshev多项式。
（3）切比雪夫Ⅱ型滤波器切比雪夫Ⅱ型滤波器在阻带呈现等波纹特性，通带单调衰减，其幅度响应为：，式中是阻带衰减达到一定数值时的最低频率。
（4）椭圆滤波器椭圆滤波器在通带和阻带都呈现波纹特性，在带内均匀波动，具有最快的滚降。
，式中为椭圆函数。
3. 冲激响应不变法所谓冲激响应不变法就是使数字滤波器的单位冲激响应序列等于模拟滤波器的单位冲激响应和的采样值，即：，其中，T为采样周期。
令为模拟系统传递函数，且，则冲激响应不变法得到的数字滤波器传递函数。
冲激响应不变法的特点是：（1）时域逼近特性良好；（2）模拟频率和数字频率呈线性关系。
（3）存在频率混叠效应，故只适用于限带的模拟滤波器。
在 MATLAB 中，可用函数 impinvar 实现从模拟滤波器到数字滤波器的冲激响应不变映射，调用格式为：[bz,az]=impinvar(b,a,fs)[bz,az]=impinvar(b,a)其中，b、a 分别为模拟滤波器的分子和分母多项式系数向量；fs为采样频率（Hz），缺省值 fs=1Hz；bz、az分别为数字滤波器分子和分母多项式系数向量。
1・信号产生函数mstg清单function xt=xtg(N)%实验五信号x(t)产生，并显示信号的幅频特性曲线%xt=xtg产生一个长度为N,冇加性高频噪声的单频调幅信号xt,N二1000., %采样频率Fs二1000Hz%载;波频率fc=Fs/10=100Hz,调制正弦波频率f0=fc/10=10Hz.N=1000;Fs=l000;T=1/Fs;Tp=N*T;t二0:T: (N-1)*T;fc=Fs/10 ;f0=fc/10; %载波频率fc=Fs/10,单频调制信号频率为f0=Fc/10;int=cos (2*pi*f0*t) ; %产生讥频止弦波调制信号mt,频率为f0ct=cos(2*pi*fc*t) ; %产生载波iF弦波信号ct,频率为fc xt=mt. *ct; %相乘产生单频调制信号xtnt=2*rand(l, N)T; %产生随机噪声nI%=======设计高通滤波器hn,用于滤除噪声nt中的低频成分，牛成高通噪声======= fp=150;fs=200;Rp=0. l;As=70; % 滤波器指标fb=[fp, fs] ;m二[0, 1]; % 计算remezord函数所需参数f, m, devdev=[107-As/20), (10" (Rp/20)-l)/(10"(Rp/20)+l)];[n, fo, mo, W]=remezord(fb, m, dev, Fs) ; % 确定rcinezP^i数所盂参数hn=rcmcz (n, fo, mo, W) ; %调用rcme函数进行设计，用J：滤除噪声nt中的低频成分yt二f订ter (hn, 1, 10*nt) ; %滤除随机噪声中低频成分，牛成高通噪声yt%========================以下为绘图部分===================================== xt=xt+yt; %噪声加信号fst=fft(xt, N);k=0:N-l;f=k/Tp;subplot (2, 1, 1) ;plot (t, xt) ;grid;xlabel(' t/s') ;ylabel (' x(t)'); axis([0, Tp/5, min(xt), max(xt)]);titleC (a)信号加噪声波形') subplot (2, 1, 2) ;plot (f, abs(fst)/max(abs (fst))) ;grid; titleC (b)信号加噪声的频谱') axis(f0, Es/2, 0, 1. 2]) ;xlabel C f/Hz');ylabel C if®度') 2•产生FIR数字滤波器设计及软件实现clear all;%==using the function ,xtg£「to plot the picture of xt and its spectrogram==xt=xtg;N=1000;fp=120; fs=150;Rp=0.2;As=60;Fs=1000; %input the defined parameters%to design the filter using th巳Windows methodwc= (fp+fs)/Fs; Ethe cut-off frequence of the filterB=2*pi*(fs-fp)/Fs; %the width of prototype filterNb=cei丄(11*pi/B); %the length of window of blackmanhn=f ir1 (Nb-1,wc,blackman(Nb));Hw=abs(fft(hn,1024)); % the frequency characteristic of the filter ywt = f ft f i]_t (hn z xt』N);%to filter xt using fftfilt%to draw the figure using the Windows methodf=[0:1023]*Fs/1024; ~figure (2)subplot(2f1,1);plot(f,20*logl0(Hw/max (Hw)));grid;xlabel ( 1f/Hz 1);ylabel(1 Amplitude 1);title ( 1 the frequency characteristic of the low-pass filter 1); axis ( [0,Fs/2z-120, 20]);t=[0:N-1]/Fs;Tp=N/Fs;subplot (2f1,2);plot (t,ywt);grid;xlabel(1t/s1);ylabel(1y_w(t) T);title ( 1 the signal waves after filtering noises 1);axis([0,Tp/2,-1,1]);%to design the filter using the best uniform approximation method fb=[fp z fs];m=[1,0];% define the parameters of remezorddev=[ (10A (Rp/20)-1)/(10A(Rp/20)+1),10A(-As/20)];[Ne z fo, mo z W]=remezord(fb,m, dev,Fs); %define the parameters of remez hn=remez(Ne,fmo z W);Hw=abs(fft(hn z1024)); % the frequency characteristic of the filteryet=fft£i1t(hn/Xt’N)；%to filter xt using filt%to draw the figure using the best uniform approximation methodf igure(3);subplot(2,1,1);f=[0:1023]*Fs/1024;plot (f, 20*logl0 (Hw/max (Hw) ) ) ; grid; xlabel ( 1 f/Hz ' ) ; ylabel ( f Amplitude 1 ); title ( 1 the frequency characteristic of the low-pass filter 1);axis([0,Fs/2,-80,10]);subplot (2, 1 z 2 ) ; plot (t, yet) ; grid; xlabel ( 11/s ' ) ; ylabel ( ' y_e (t) 1 ); title ( 1 the signal waves after filtering noises');axis([0,Tp/2,-1,1]);⑻信号加噪声波形105e oX-5-100 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2t/s(b)信号加噪声的频谱1® 0.50 50 100 150 200 250 300 350 400 450 500f/Hz-800 50 100 150 200 250 300 350400 450 500f/Hzthe signal waws after filtering noises050.5 0 0 0.05 0.1 0.15 0.2 0.250.3 0.35 0.4 0.45 0.5 t/s 0-20-40-60the frequency characteristic of the low-pass filter。
