向量的基本概念

向量的基本概念
向量是线性代数中的基本概念之一，它是指一个有大小和方向的量。

向量通常用箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。

向量可以用坐标表示，也可以用向量的起点和终点表示。

向量的大小也称为向量的模或长度，它表示向量的大小，通常用||v|| 表示。

向量的方向表示向量的朝向，可以用角度或者方向余弦表示。

向量的起点和终点表示向量的位置，起点表示向量的起点，终点表示向量的终点。

向量可以进行加法和数乘运算。

向量的加法表示将两个向量的大小和方向相加，得到一个新的向量。

向量的数乘表示将一个向量乘以一个标量，得到一个新的向量，新向量的大小为原向量的大小乘以标量，方向不变或者相反。

向量可以用于表示物理量，如力、速度、位移等。

在计算机图形学、机器学习等领域，向量也被广泛应用。

总之，向量是一个有大小和方向的量，它可以用坐标或者起点和终点表示，可以进行加法和数乘运算，可以表示物理量和应用于计算机科学等领域。

向量基本概念及坐标表示1、向量：既有大小，又有方向的量.零向量：长度为0的向量.单位向量：长度等于1个单位的向量.平行向量(共线向量)：方向相同或相反的非零向量.零向量与任一向量平行.相等向量：长度相等且方向相同的向量.2、 (1)向量既有大小又有方向的量。

(2)向量的模一一有向线段的长度，|a|(3)单位向量|a o| 1, a o —|a|(4)零向量0 , |0| 0在此规定下向量可以在平面(或空间)平行移动而不改变3、共线向量(平行向量) 方向相同或相反的向量。

规定零向量与任意向量平行。

(5)相等的向量长度相等方向相同b // a (b 0) 存在唯一实数，使b aOA OB OC OA OB BA3.与向量 d （12,5）平行的单位向量为 （）12 A.占,5) 13 C( 12 5、十 / 12 5 C.(一，)或(，B.D ・( 12 513' 1312 513' 13 5、平面向量基本定理（向量的分解定理）e i , e 2是平面内的两个不共线向量，a 为该平面任一向量，则存在唯一实数对1、 2，使得a 1e i2e 2 ， e i 、e 2叫做表示这一平面内所有向量的一组基底。

6向量的坐标表示i ，j 是一对互相垂直的单位向量，则有且只有一对实数 x ，y ，使得a x i y j ，称（x , y ）为向量a 的坐标，记作：a x ，y ，即为向量的坐标 表示。

设 a x 1， y 1， b X 2， y 2贝 y a b x 1，y 1y 1, y 2 x1y 1， X 2 y 2aX" y 1X 1, y 1若A x 1，y 1，B x 2，y 2则 AB X 2 X 1，y Y 1练习题：1.将—[2(2 a 8b) 4(4 a12A. 2a bB.C. a b D .2.如图 1所示，向量OA,OB,C ）C 的终点A, B ，C 在一条直线上，且nnOAp ，mu OBq ，O C r ，则以下等式中成立的是（A. r3 312q B.r p 2qc. r尹 2qD.2p2b ）］化简成最简式为（2b ab a f图IuurACUUU 3CB ，设4. 已知向量a (2,3),b(1,2)，若ma nb 与a 2b 共线，则m等于()n11A. 1B.2C.丄 D.-2225 •已知非零向量 u 和e 2不共线，欲使te i e 2和◎ t e ?共线，则实数t 的值为 _______ •6•平行四边形ABCD 中，M 为DC 中点，N 为BC 的中点•设AB a ， AD b ，,BJUD则MN _____________ (用a ， b 表示).7. 已知向量 a (3,1),b (1,3),c (k,7)，若(a c)//b,则k _____________ 8. 设向量a (1,2),b (2,3)，若向量 a b 与向量C (4,7)共线，则 = ______9. 两个非零向量厲，e 2不共线.ujuuur ium,「「八(1) 若 AB ee 2，BC2e 1 8e 2，CD3(©e 2)，求证：A B ，D 三点共线;(2) 求实数k ，使k e 1 e 2与2e k e ：共线.uuu10 .已知Y ABCD 的对角线AC 和BD 相交于O ，且OAUUU UUU UULTUUUb 分别表示向量OC ，OD ，DC ，BC .错误!未找到引用源若A 、B 、D 三点共线，求k 的值.11、设0(2是两个不共线的向量,AB 2ei ke 2 ,CB e 13e 2, CD 2e 1e 2，uuua ，OBb ，用向量a ，12.已知向量 a ( 3,2),b (2,1),c (3, 1),t R.若a tb与c共线，求实数t.。

向量的基本概念及其应用向量是高中数学和物理学中一个非常重要的概念，也被广泛地应用于计算机科学和工程学中。

在本文中，我们将讨论向量的基本概念及其应用，并从几个不同的角度来探讨这个概念。

一、什么是向量向量是一个有方向和大小的量。

它通常用箭头表示，箭头的方向表示向量的方向，箭头的长度表示向量的大小。

一个向量通常由两个分量表示，即水平分量和垂直分量。

水平分量是向量在水平方向上的长度，垂直分量是向量在垂直方向上的长度。

向量的长度可以通过勾股定理计算，即 length = sqrt(x^2+y^2)。

二、向量的基本属性向量有几个基本属性，包括加法、减法、数量积和向量积等。

向量的加法定义为从一个向量的尾部到另一个向量的头部的箭头之间绘制一条新的向量。

向量的减法定义为从一个向量的头部到另一个向量的头部之间绘制一条新的向量，并将其指向第二个向量的尾部。

数量积是向量的点积，它定义为两个向量的元素逐个相乘并相加的结果。

向量积是两个向量的叉积，它定义为两个向量垂直于彼此并且其大小等于两个向量的元素积的向量。

三、向量的应用向量在许多领域中都有应用，包括物理学、计算机科学和工程学等。

在这些领域中，向量通常用于计算和表示对象之间的关系。

物理学中，向量常用于描述力、速度和加速度等现象。

例如，在计算机模拟中，向量可以用于表示移动的物体的速度和方向，以及与其互动的物体之间的相对位置。

在计算机科学中，向量广泛用于计算机图形学和机器学习中。

在计算机图形学中，向量通常用于描述三维空间中的点和方向。

在机器学习中，向量通常用于表示特征向量，这些向量可以用于分类和聚类等任务。

工程学中，向量通常用于计算和表示力和位移等物理量。

例如，在建筑设计中，向量可以用于表示结构中各部件之间的关系，以及在运动控制系统中，向量可以用于描述机器人臂的位置和末端执行器的移动。

结论向量是一个有方向和大小的量。

它通常用箭头表示，箭头的方向表示向量的方向，箭头的长度表示向量的大小。

向量代数的基本概念及运算法则向量代数是线性代数的重要部分，涉及了向量的基本概念及其运算法则。

本文将介绍向量的概念、向量的加法和减法运算法则、向量的数乘运算法则，并讨论一些常见的向量运算性质。

一、向量的概念向量是具有大小和方向的物理量，常用有向线段表示。

通常将向量用字母加箭头表示，例如，向量a用记号“→a”表示。

向量有两个重要的属性，即大小（模）和方向。

向量的大小表示向量的长度或大小，用|→a| 或||→a|| 表示，读作“模a”或“a的模”。

向量的方向表示指向何处，可以用角度、弧度或者其他方式进行表示。

二、向量的加法和减法运算法则向量的加法运算是指将两个向量进行求和的运算，其法则可以用平行四边形法则和三角法则表示。

平行四边形法则可以简要描述如下：设有向量→a和→b，取→a的起点作为平行四边形的一个顶点，将→b 平移至→a的终点，以→a和→b的起点为相对顶点形成平行四边形，平行四边形的对角线所表示的向量，即为向量→a和→b的和向量→a+→b。

三角法则可以简要描述如下：将→a和→b的起点相接，以→a的终点为直角，连接→b的终点和→a的起点，所得的向量即为向量→a和→b的和向量→a+→b。

向量的减法运算是指将两个向量进行相减的运算，可以通过向量的加法和取负得到。

设有向量→a和→b，向量→a减去向量→b即为向量→a加上向量→b的负向量，即→a-→b=→a+(-→b)。

三、向量的数乘运算法则向量的数乘运算是指将一个向量乘以一个实数的运算，用以改变向量的长度或方向。

设有向量→a和实数k，向量→a与k的乘积，记作k→a，即为把向量→a的长度伸缩为原来的|k|倍，并在原来的方向上（若k>0）或相反方向上（若k<0）。

四、常见的向量运算性质1. 交换律：向量加法满足交换律，即→a+→b=→b+→a。

2. 结合律：向量加法满足结合律，即(→a+→b)+→c=→a+(→b+→c)。

3. 分配律：向量的数乘运算满足分配律，即k(→a+→b)=k→a+k→b。

高中数学向量知识总结向量是高中数学中的一个重要概念，其在几何和代数中都具有广泛的应用。

本文将对高中数学向量知识进行总结，包括向量的基本概念、向量的表示与运算、向量的内积与外积等内容。

一、向量的基本概念向量是有方向和大小的量，常用箭头表示。

在直角坐标系中，向量可以表示为一个有序数对。

向量的大小通常使用绝对值或模表示，用||AB||或|AB|表示。

二、向量的表示与运算1. 向量的表示：向量AB可以表示为AB→或→AB，其中箭头方向表示向量的方向。

向量可以通过其起点和终点表示，也可以通过坐标表示。

2. 向量的加法：向量的加法满足平行四边形法则，即将一个向量的起点放在另一个向量的终点上，连接两个向量的起点和终点形成的向量为它们的和。

3. 向量的减法：向量的减法可以看作是加上一个相反向量，即A - B = A + (-B)。

4. 向量的数量积：向量的数量积（又称点积、内积）表示两个向量的相似程度，可以用来判断两个向量的夹角是否为直角。

向量的数量积定义为两个向量的模的乘积与它们的夹角的余弦值的乘积。

设向量A和B的夹角为θ，则数量积的计算公式为：A·B = |A|·|B|·cosθ。

5. 向量的向量积：向量的向量积（又称叉积、外积）是一个向量，其大小等于由两个向量构成的平行四边形的面积，方向垂直于这两个向量所构成的平面。

向量的向量积可以用来求解三角形的面积。

设向量A和B的夹角为θ，则向量积的计算公式为：A×B = |A|·|B|·sinθ·n，其中n为单位法向量。

三、向量的性质与应用1. 平行向量的性质：如果两个向量的方向相同或相反，则它们为平行向量。

平行向量的数量积等于两个向量模的乘积。

2. 垂直向量的性质：如果两个向量的数量积为0，则它们为垂直向量。

3. 共线向量的性质：如果一个向量与另一个向量的倍数相等，则它们为共线向量。

4. 向量的应用：向量在几何和物理中具有广泛的应用，例如用向量可以描述力的大小和方向、表示平面内的线性方程等。

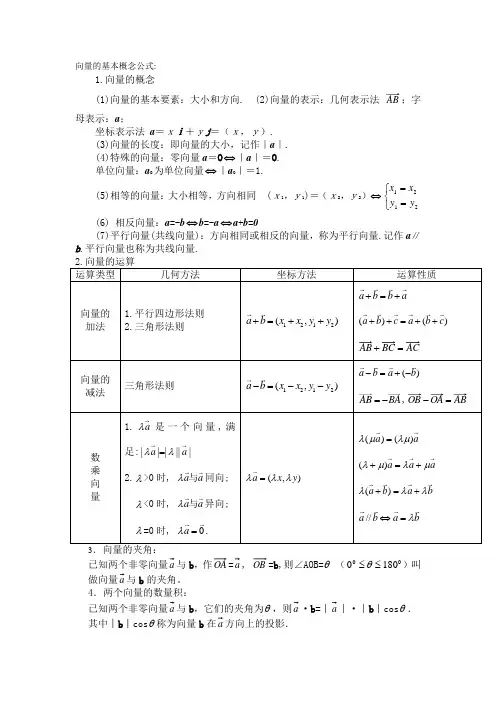
向量的基本概念公式:1.向量的概念(1)向量的基本要素：大小和方向.(2)向量的表示：几何表示法 AB ；字母表示：a ；坐标表示法 a ＝ｘｉ＋ｙj ＝（ｘ，ｙ）. (3)向量的长度：即向量的大小，记作｜a ｜. (4)特殊的向量：零向量a ＝O ⇔｜a ｜＝O . 单位向量：a O 为单位向量⇔｜a O ｜＝1.(5)相等的向量：大小相等，方向相同(ｘ1，ｙ1)＝（ｘ2，ｙ2）⎩⎨⎧==⇔2121y y x x(6) 相反向量：a =-b ⇔b =-a ⇔a +b =0(7)平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作a ∥b .平行向量也称为共线向量. 运算类型 几何方法 坐标方法 运算性质向量的 加法 1.平行四边形法则 2.三角形法则1212(,)a b x x y y +=++a b b a +=+()()a b c a b c ++=++AC BC AB =+向量的减法三角形法则1212(,)a b x x y y -=--()a b a b -=+-AB BA =-,AB OA OB =-数 乘 向 量1.a λ是一个向量,满足:||||||a a λλ=2.λ>0时, a a λ与同向; λ<0时, a a λ与异向;λ=0时, 0a λ=.(,)a x y λλλ=()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+//a b a b λ⇔=3已知两个非零向量a 与b ，作OA =a , OB =b ,则∠AOB=θ （001800≤≤θ）叫做向量a 与b 的夹角。

4．两个向量的数量积：已知两个非零向量a 与b ，它们的夹角为θ，则a ·b =︱a ︱·︱b ︱cos θ． 其中︱b ︱cos θ称为向量b 在a 方向上的投影．5．向量的数量积的性质：若a =（11,y x ）,b =（22,y x ）则e ·a =a ·e =︱a ︱cos θ (e 为单位向量);a ⊥b ⇔a ·b =0⇔12120x x y y +=（a ，b 为非零向量）;︱a ︱=2211a a x y •=+;cos θ=a ba b ••=121222221122x x y y x y x y ++⋅+． 6 ．向量的数量积的运算律：a ·b =b ·a ;(λa )·b =λ(a ·b )=a ·(λb );(a ＋b )·c =a ·c +b ·c ．7.重要定理、公式(1)平面向量基本定理e 1，e 2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数λ1， λ2，使a ＝λ1e 1＋λ2e 2.(2)两个向量平行的充要条件a ∥b ⇔a ＝λb (b ≠0)⇔x 1y 2－x 2y 1＝O. (3)两个向量垂直的充要条件 a ⊥b ⇔a ·b ＝O ⇔x 1x 2＋y 1y 2＝O. (4)线段的定比分点公式设点P 分有向线段21P P 所成的比为λ，即P P 1＝λ2PP，则⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式)当λ＝1时，得中点公式：OP ＝21（1OP ＋2OP ）或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x。

向量的分解知识点总结一、向量的基本概念向量是向量代数中的基本概念之一，它是具有大小和方向的量，通常用箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。

向量可以在数学、物理、工程等领域中广泛应用，是研究力、速度、位移、位矢等物理量的重要工具。

在二维空间中，向量通常用坐标表示，如向量a=(a1,a2)表示在x轴方向的分量为a1，在y轴方向的分量为a2。

在三维空间中，向量可以用三个坐标表示，如向量a=(a1,a2,a3)表示在x轴、y轴和z轴方向的分量分别为a1、a2和a3。

除了用坐标表示，向量还可以用向量的模和方向角表示。

向量的模表示向量的大小，用|a|或||a||表示，向量的方向角表示向量与坐标轴之间的夹角，通常用α、β、γ表示。

二、向量的线性组合向量的线性组合是向量代数中的一个重要概念，它是指将若干个向量按照一定的比例相加得到的新向量。

设有n个向量a1,a2,...,an，实数λ1,λ2,...,λn，称向量b=λ1a1+λ2a2+...+λnan 为向量a1,a2,...,an的线性组合，其中λ1,λ2,...,λn称为向量a1,a2,...,an的系数。

向量的线性组合具有以下性质：1. 交换律：对于任意向量a,b，有a+b=b+a。

2. 结合律：对于任意向量a,b,c，有a+(b+c)=(a+b)+c。

3. 数乘结合律：对于任意向量a,实数λ,μ，有(λμ)a=λ(μa)。

4. 数乘分配律：对于任意向量a,b,实数λ,μ，有λ(a+b)=λa+λb。

5. 向量加法和数乘运算满足分配律。

三、向量的分解向量的分解是指将一个向量分解成若干个向量的线性组合，常见的向量分解有向量的基底分解和向量的正交分解。

1. 向量的基底分解设有向量a和一组线性无关的向量b1,b2,...,bn，如果向量a可以表示为向量b1,b2,...,bn的线性组合，即a=λ1b1+λ2b2+...+λnbn，则称向量a关于向量b1,b2,...,bn的基底分解。

总结向量公式定理知识点一、向量的基本概念和性质1. 向量的定义向量是一个有大小和方向的量，通常用箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。

在数学上，通常用有序数组或列向量表示一个向量，例如，向量a可以表示为(a1, a2, a3)或者[a1 a2 a3]。

2. 向量的性质向量有一些基本的性质，例如：（1）相等性：如果两个向量的大小和方向都相等，则它们是相等的；（2）共线性：如果两个向量的方向相同或者相反，则它们是共线的；（3）线性运算：向量可以进行加法和数乘运算，满足加法交换律、结合律和数乘结合律。

二、向量的运算和计算1. 向量的加法向量的加法是指两个向量相加，结果是一个新的向量。

两个向量的加法可以用三角法则或者平行四边形法则进行计算。

2. 向量的数乘向量的数乘是指一个向量乘以一个数，结果是一个新的向量。

向量的数乘可以用数乘的分配律和结合律进行计算。

3. 向量的点积向量的点积（也称为数量积或内积）是指两个向量相乘得到一个标量。

向量的点积有一些重要的性质，例如满足交换律、分配律和结合律。

4. 向量的叉积向量的叉积（也称为向量积或外积）是指两个向量相乘得到一个新的向量。

向量的叉积也有一些重要的性质，例如满足反交换律和结合律。

三、向量的公式和定理1. 向量的模长公式向量的模长表示向量的大小，通常用||a||表示。

向量的模长可以用勾股定理进行计算，即||a|| = √(a1^2 + a2^2 + a3^2)。

2. 向量的角度公式两个向量的夹角可以通过它们的点积和模长进行计算，即cosθ = (a·b) / (||a|| · ||b||)。

3. 平面向量的基本定理平面向量的基本定理包括平面向量的线性组合和平面向量的共线定理。

平面向量的线性组合指的是两个向量的线性组合仍然是一个向量，满足封闭性和结合律。

平面向量的共线定理指的是如果两个向量共线，则它们的线性组合也是共线的。

向量的根本概念公式:1.向量的概念(1)向量的根本要素：大小和方向.(2)向量的表示：几何表示法 AB ；字母表示：a ；坐标表示法 a ＝ｘｉ＋ｙj ＝〔ｘ，ｙ〕. (3)向量的长度：即向量的大小，记作｜a ｜. (4)特殊的向量：零向量a ＝O ⇔｜a ｜＝O . 单位向量：a O 为单位向量⇔｜a O ｜＝1.(5)相等的向量：大小相等，方向相同(ｘ1，ｙ1)＝〔ｘ2，ｙ2〕⎩⎨⎧==⇔2121y y x x(6) 相反向量：a =-b ⇔b =-a ⇔a +b =0 (7a ∥b .平行向量也称为共线向量. 运算类型 几何方法坐标方法 运算性质向量的 加法1212(,)a b x x y y +=++a b b a +=+()()a b c a b c ++=++AC BC AB =+向量的减法三角形法那么1212(,)a b x x y y -=--()a b a b -=+-AB BA =-,AB OA OB =-数 乘 向 量1.a λ是一个向量,满足:||||||a a λλ=2.λ>0时, a a λ与同向; λ<0时, a a λ与异向;λ=0时, 0a λ=.(,)a x y λλλ=()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+//a b a b λ⇔=3两个非零向量a 与b ，作OA =a , OB =b ,那么∠AOB=θ 〔001800≤≤θ〕叫做向量a 与b 的夹角。

4．两个向量的数量积：两个非零向量a 与b ，它们的夹角为θ，那么a ·b =︱a ︱·︱b ︱cos θ． 其中︱b ︱cos θ称为向量b 在a 方向上的投影． 5．向量的数量积的性质：假设a =〔11,y x 〕,b =〔22,y x 〕那么e ·a =a ·e =︱a ︱cos θ (e 为单位向量);a ⊥b ⇔a ·b =0⇔12120x x y y +=〔a ，b 为非零向量〕;︱a ︱=2211a a x y •=+;cos θ=a ba b ••=121222221122x x y y x y x y ++⋅+． 6 ．向量的数量积的运算律：a ·b =b ·a ;(λa )·b =λ(a ·b )=a ·(λb );(a ＋b )·c =a ·c +b ·c ．7.重要定理、公式(1)平面向量根本定理e 1，e 2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数λ1， λ2，使a ＝λ1e 1＋λ2e 2.(2)两个向量平行的充要条件a ∥b ⇔a ＝λb (b ≠0)⇔x 1y 2－x 2y 1＝O. (3)两个向量垂直的充要条件 a ⊥b ⇔a ·b ＝O ⇔x 1x 2＋y 1y 2＝O. (4)线段的定比分点公式设点P 分有向线段21P P 所成的比为λ，即P P 1＝λ2PP ，那么⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式)当λ＝1时，得中点公式：OP ＝21〔1OP ＋2OP 〕或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x。

数学必背向量知识点数学必背向量知识点1.向量的基本概念(1)向量既有大小又有方向的量叫做向量.物理学中又叫做矢量.如力、速度、加速度、位移就是向量.向量可以用一条有向线段(带有方向的线段)来表示，用有向线段的长度表示向量的大小，用箭头所指的方向表示向量的方向.向量也可以用一个小写字母a，b，c表示，或用两个大写字母加表示(其中前面的字母为起点，后面的字母为终点)(5)平行向量方向相同或相反的非零向量，叫做平行向量.平行向量也叫做共线向量.若向量a、b平行，记作a∥b.规定：0与任一向量平行.(6)相等向量长度相等且方向相同的向量叫做相等向量.①向量相等有两个要素：一是长度相等，二是方向相同，二者缺一不可.②向量a，b相等记作a=b.③零向量都相等.④任何两个相等的非零向量，都可用同一有向线段表示，但特别要注意向量相等与有向线段的起点无关.2.对于向量概念需注意(1)向量是区别于数量的一种量，既有大小，又有方向，任意两个向量不能比较大小，只可以判断它们是否相等，但向量的模可以比较大小.(2)向量共线与表示它们的有向线段共线不同.向量共线时，表示向量的有向线段可以是平行的，不一定在同一条直线上;而有向线段共线则是指线段必须在同一条直线上.(3)由向量相等的定义可知，对于一个向量，只要不改变它的大小和方向，它是可以任意平行移动的，因此用有向线段表示向量时，可以任意选取有向线段的起点，由此也可得到：任意一组平行向量都可以平移到同一条直线上.3.向量的运算律(1)交换律：α+β=β+α(2)结合律：(α+β)+γ=α+(β+γ)(3)数量加法的分配律：(λ+μ)α=λα+μα(4)向量加法的分配律：γ(α+β)=γα+γβ高中数学学习方法掌握数学学习实践阶段:在高中数学学习过程中,我们需要使用正确的学习方法,以及科学合理的学习规则。

先生著名的日本教育在米山国藏在他的数学精神、思想和方法,曾经说过,尤其是高阶段的数学学习数学,必须遵循“分层原则”和“循序渐进”的原则。

向量基本概念
向量是最基本的数学工具之一，它广泛应用于物理、工程、计算机科学等领域。

本文将介绍向量的基本定义、表示方法以及相加、相减、数量积、向量积等运算。

一、向量的定义
向量是空间中具有大小和方向的量，一般用箭头表示。

它由两个端点确定，可以表示为有序的数对或坐标。

二、向量的表示方法
1. 点表示法：将一个向量的起点放在坐标原点O，将终点放在坐标系内的某个点，然后用有向线段或箭头表示向量。

2. 坐标表示法：将向量的起点放在坐标原点O，终点坐标用有序数对(x,y,z)表示。

三、向量的运算
1. 向量相加：将两个向量的末端相接，以它们的起点作为相加后向量的起点，终点作为相加后向量的终点。

2. 向量相减：将一个向量的相反向量加到另一个向量上，即将相反向量变为相应向量再相加。

3. 数量积：两个向量的数量积也叫点积，记为a·b，其结果是一个标量，表示两个向量之间的夹角余弦值乘以两个向量的模长之积。

4. 向量积：两个向量的向量积也叫叉积，记为a×b，其结果是一个向量，垂直于两个向量所在的平面，并且符合右手法则。

四、小结
向量是数学学科中最基础的概念之一。

通过点表示法和坐标表示法，可以表示向量的大小、方向和位置。

向量的相加、相减、数量积和向量积是向量最基本的运算，它们在物理、工程、计算机科学等领域中具有广泛的应用。

向量的基本概念与线性运算1. 向量的基本概念: 向量、零向量、单位向量、平行向量（共线向量）、相等向量、相反向量. 表示方法：2. 向量的基本运算：向量加法：向量加法有“三角形法则”与“平行四边形法则”。

（向量的减法）3.实数与向量的积：实数λ与向量→a 的积是一个向量，记作：λ→a（1）||||||→→=a a λλ；（2）λ>0时λ→a 与a 方向相同；λ<0时λ→a 与a 方向相反；λ=0时λ→a =→0； （3）运算定律 .)(,)(,)()(→→→→→→→→→+=++=+=b a b a a a a a a λλλμλμλλμμλ 4 两个向量共线定理：向量b 与非零向量a 共线⇔有且只有一个实数λ，使得b =a λ 5 平面向量的基本定理：如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数21,λλ使：2211e e a λλ+=，其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底 练习题例1 给出下列命题：① 若|a |＝|b |，则a =b ；② 若A ，B ，C ，D 是不共线的四点，则AB DC =当且仅当四边形ABCD 为平行四边形；③ 若a =b ，b =c ，则a =c ，④a =b 的充要条件是|a |=|b |且a //b ；⑤ 若a //b ，b //c ，则a //c ，其中正确的序号是例2 设A 、B 、C 、D 、O 是平面上的任意五点，试化简： ①AB BC CD ++；②DB AC BD ++；③OA OC OB CO --+- 例3 已知正方形ABCD 边长为1，,,,→→→→→→===c AC b BC a AB 则→→→++c b a 的模等于例4 a 、b 是非零向量，指出下列等式成立的条件：a b a b +=+； a b a b +=-； a b a b +=-； a b a b -=-。