当前位置：文档之家 › 定解条件初始条件

定解条件初始条件

  • 格式：ppt
  • 大小：213.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

偏微分方程的定解条件与解的存在唯一性

偏微分方程的定解条件与解的存在唯一性

偏微分方程的定解条件与解的存在唯一性偏微分方程（Partial Differential Equation, 简称PDE）是数学领域中的重要研究对象，广泛应用于物理学、工程学、金融学等领域。

在求解偏微分方程时，我们需要考虑定解条件，以确保解的存在和唯一性。

本文将探讨偏微分方程的定解条件，并讨论解的存在唯一性。

一、偏微分方程的定解条件在求解偏微分方程之前，我们需要明确的是问题的定解条件。

定解条件是指在区域Ω上关于未知函数u及其偏导数的附加条件。

常见的定解条件包括初始条件和边界条件。

1. 初始条件（Initial Condition）初始条件是在区域Ω的某个子集Ω₀上给定的函数值及其偏导数，常用符号表示为u(x, t₀) = g(x, t₀)，其中g(x, t₀)为已知函数，t₀为给定的初始时间。

2. 边界条件（Boundary Condition）边界条件是在区域Ω的边界上给定的函数值及其偏导数，常用符号表示为u(x, t) = f(x, t)，其中f(x, t)为已知函数。

在一些情况下，还需要考虑特殊的边界条件，如周期性边界（Periodic Boundary Conditions）和运动边界（Moving Boundary Conditions）等。

二、解的存在唯一性偏微分方程的解的存在唯一性是指在给定的定解条件下，方程是否有解以及解是否唯一。

1. 解的存在性对于某些偏微分方程，我们可以通过适当的数学工具（如变分法、分离变量法、线性化等）证明其存在解。

然而，并非所有的偏微分方程都具备解的存在性，存在着某些无解的情况。

因此，对于求解偏微分方程问题，我们需要首先考虑其解的存在性。

2. 解的唯一性在一些情况下，即使偏微分方程存在解，其解也不一定是唯一的。

对于线性偏微分方程，我们可以通过使用变分法或利用极大模原理来证明解的唯一性。

而非线性偏微分方程的唯一性则比较复杂，通常需要借助于更加深入的分析和数学工具。

定解条件

定解条件

自由冷却：规定了从杆端流出的热流强度(-kun )与温度差（u xa -）
之间的关系。
即：-kun xa h(u xa - ), h : 热交换系数
即：(u Hun ) xa ,
Hk n
若说杆的两端自由冷却：在x = l端,nˆ即xˆ,(u Hux ) xl 在x = 0端,nˆ即-xˆ,(u Hux ) x0
若h ? k,即：H 0,则u 0 (退化为第一类边界条件) x0 u 0 xl
又如：作纵振动杆，在某一端点x = a既非固定也非自由而是通过弹性联结体 连接到固定物上。
弹性联结：规定杆中弹性力（YSun）等于弹性连接物中的弹性恢复力 (-ku, k为劲度系数)
YSun xa ku xa
即：(u+ YS k
以上边界条件都是线性的(u,ux都为一次的) 其中f 0的边界条件又叫齐次的。除此以外，还有其它类边界条件。
杆的一端挂有重物作纵振动。
对重物有：Mg T Ma Mutt T M (g utt )
杆端受力T '， 对杆端有：YS ux xl T ' Mg M utt xl
T T’ 边界条件中出现了u对x,u对t的偏导数。
x l
u x0 0，ux xl 0
例：细杆导热：qv
ku,
从u高
u低，u
v i
u
v j
u
v k
u
x y z
nˆ(xv)
nˆ(xv)
u u n x
u u x
n x
若杆的某端点x = a有热流f (t)沿该端点外法线方向流出： －kun xa f (t) 若杆的某端点x = a有热流f (t)沿该端点外法线方向流入： －kun xa －f (t) 若端点绝热：un xa 0

D5-2 定解条件

D5-2 定解条件

x 0 为原点， 取弦的水平位置为 x 轴，
弦作自由（无外力）横振动，所以泛定方程为齐次波动方程
utt a2uxx 0
(2)确定边界条件 对于弦的固定端，显然有 u(x,t)|x=0=0, ux(x,t)|x=l=0 另一端自由，意味着弦的张力为零．则
2016/9/30
u x x , t x l 0
定义：系统的物理量在边界上具有的情况。
常见的线性边界条件分为三类：
A.第一类（狄利克雷）边界条件 给出未知函数在边界上的函数值。
例2：两端固定的弦振动时的边界条件：
u( x, t )
x 0
0
和
u( x, t )
x l
0
2016/9/30
4
例3：细杆热传导
x0
xl
细杆x=l端的温度处于恒温状态,边界的数理方程
h
· ·
状如图所示,且弦处于静止状态，即有方程
l x
l/2
初始速度 ut ( x, t ) 初始位移 u( x , t )
t 0
t 0
2016/9/30
2h x l 2h ( l x ) l
0
l x [0, ] 2 l x [ , l ] 23
（二）边界条件
ku YSux
x l
弹性力： f ku
则在端点
(u
YS ux ) k
0
u ) n
xl
f ( x0 , y0 , z0 , t )
x
第三类边界条件的基本形式： (u H
边界x0 , y0 , z0
这些是最常见的线性边界条件，还有其它形式。
（三）衔接条件

《流体力学》课件 1.17 定解条件

《流体力学》课件 1.17 定解条件

k
T n
介质 2
（三）、固壁边界处
1. 能量边界条件
Tf Tw
k
T n
f
k T n w
2. 速度边界条件
（1） 切向速度
Vf Vf
Vw Vw
粘性流体 理想流体
（2）法向速度
n
Vf
n
Vw
Fx, y, z,t 0 Fx dx, y dy, z dz,t dt 0
1 R2
1 0
sij2 in j 0
p
1
p2
22
sij2ni
n
j
1 3
skk2
1 R1
1 R2
忽略表面张力
sij2 in j 0
p
2
2
2
sij2
ni
n
j
1 3
skk2
p0
2. 运动学边界条件
n
V1
n
V2
例题：试写出如图所示自由液面 波动的运动学边界条件。
答：设自由面方程为
F内 x 0t 2 y2 a2 0，F外 x2 y2 b2 0
1. 无粘流体在内、外圆柱面上的速度边界条件
F内 x
uf
F内 y
f
F内 z
wf
F内 t
0
F外
x
uf
F外 y
f
F外 z
wf
F外 t
0
x
uf
0
x0 0 u f
内圆柱体边界
y f 0
xu f y f
定解条件
一、初始条件
V
r,t0源自V1r，pr,
t
0
p1 r ， r, t 0

微分方程的定解条件与特殊解法

微分方程的定解条件与特殊解法

定义：在定解区 间的闭区间端点 上，微分方程的 解必须满足一定 的连续性条件。
类型：对于一阶 微分方程，连续 性条件包括自然 边界条件、周期 边界条件等。
作用：连续性条 件是保证微分方 程解的连续性和 物理意义的重要 条件。
应用：在解决实 际问题时，需要 根据具体问题的 性质和要求，选 择适当的连续性 条件。
PART THREE
定义：欧拉方法是微分方程数值解法的一种，通过离散化微分方程，用差分代替微分，得到离 散化的数值解。
原理：利用已知的初值条件，逐步推算出微分方程的解在各个离散点上的近似值。
步骤：先确定初始值，然后按照一定的步长逐步计算出各个离散点上的近似解。
优缺点：欧拉方法简单易懂，易于实现，但精度较低，稳定性较差。
描述生物系统的动态行为
生理学和病理学中的数学模型
添加标题
添加标题
药物设计和药物动力学
添加标题
添加标题
医学影像和信号处理
汇报人：XX
优点：计算简单、易于编程实现、精度可控等。
PART FOUR
力学：描述物体运动规律，如万有引力定律、牛顿第二定律等。 电磁学：解释电磁场的变化规律，如麦克斯韦方程组等。 热学：研究热量传递规律，如热传导方程等。 波动：描述波动现象，如波动方程等。
航空航天：飞行器设计和优化中的气动动力学方程求解 机械工程：机器人运动轨迹规划和控制算法的微分方程求解 化学工程：化学反应动力学模型和传递过程的动力学方程求解 交通工程：交通流理论和车辆动力学的微分方程求解
注意事项：需要满 足一定的条件才能 使用分离变量法
定义：通过引入新的变量来简化微分方程的形式，从而求解微分方程的方法。 适用范围：适用于形式较为复杂的微分方程，特别是难以直接求解的方程。 常用方法：常见的变量代换法包括三角代换、指数代换等。 实例：通过变量代换法，可以将一些复杂的微分方程转化为容易求解的形式。

7-2定解条件

7-2定解条件

解：初始位移
初始速度
u
t0
tan
x
tan
l
x
x
l 2
xห้องสมุดไป่ตู้
l 2
u 0 （还没来得及运动） t t0
3. 稳定方程：与时间无关，没有初始条件
二. 边界条件 描述边界上各点在任一时刻的状况.
1. 弦振动边界条件 例如两端固定的弦：
2. 杆振动边界条件 ①两端固定的杆：
u u
x0 xl
0 0
t≥0
数学物理方法
定解条件
丁成祥
§7.2 定解条件
一. 初始条件 给出初始时刻（t=0）介质上任一质点的状况.
1. 对波动方程，要给出初始位移和初始速度
u t0 x, y, z
u t
t0
x, y, z
2. 对于热传导方程，只须给出初始时刻的温度分布
u t0 x, y, z
例. 如右图所示，将弦轻轻拉起，再突然放开，试写出振动方程的初始条件（θ 很小）.
H k
u
xl
H k
u0
或
u x
hu
xl
hu0
此为初稿，疏漏之处，敬请指正
数学物理方法
类型 一类 二类
三类
定解条件
丁成祥
总结：三类边界条件
表达式
u (,t)
u f (,t) n
u n
hu
f
(, t )
此为初稿，疏漏之处，敬请指正
“流出”，而非“流入”，或者说“流入为负”. 如果左端绝热，则边界条件为
③边界按“牛顿冷却定律”散热；则
u 0 x x0
k
u n
H[u(,t) u0 ]

初始条件与边界条件

初始条件与边界条件

x0
xl
若弦的两端不是固定的，而是按照规律 u1(t), u2(t) 在运动,则其边界条件为
u x0 u1(t ); u xl u2 (t )
热传导问题：当物体与外界接触的表面温度 f(M,t) 已知时，其边界条件为
u f (M,t) S
第二类边界条件：给出 u 沿 S 的外法线方向的
ut a2uxx 0
u |t0 ( x)
( x ,t 0) ( x )
热传导方程的Cauchy问题
utt u |t

0
a 2uxx
(x
)
0
ut |t0 ( x)
( x ,t 0) ( x )
0, 0 0, 0 0, 0
第一类边界条件 第二类边界条件 第三类边界条件
§1.3 定解问题的提法
初始条件和边界条件都称为定解条件。 定解问题是指偏微分方程和相应定解条件的结合体。
偏微分方程和相应初始条件构成的定解问题称为初 值问题或者柯西(Cauchy)问题。
边界条件是给出具体物理现象在边界上所处的物 理情况。根据边界条件数学表达方式的不同，一 般把边界条件分为三类。设 u 是未知函数，S 为边界，则分类如下：
第一类边界条件：直接给出 u 在边界 S 上的值
u S

f1 .
弦振动问题：如果弦的两端是固定的，也就是说 端点无位移，则其边界条件为
u 0; u 0
(x, y,z)

uzz )

0
(u u) f ( x, y, z, t )
n

(x, y,z) ,t 0 (x, y,z)

定解条件和定解问题

定解条件和定解问题

定解条件与定解问题含有未知函数得偏导数得方程叫偏微分方程,常微分方程可以瞧成就是特殊得偏微分方程。

方程得分数就是1得称为方程式,个数多于1得叫做方程组。

方程（组)中出现得未知函数得最高阶偏导数得阶数称为方程(组)得阶数。

如果方程(组)中得项关于未知函数及其各阶偏导数得整体来讲就是线性得，就称方程(组)为线性得,否则就称为非线性得。

非线性又分为半线性、拟线性与完全非线性。

一、定解条件给定一个常微分方程,有通解与特解得概念。

通解只要求满足方程,即满足某种物理定律,而不能完全确定一个物理状态。

特解除了要求满足方程还要满足给定得外加(特殊)条件。

对偏微分方程也就是如此,换句话说，只有偏微分方程还不足以确定一个物理量随空间与时间得变化规律,因为在特定情况下这个物理量还与它得初始状态与它在边界受到得约束有关。

描述初始时刻得物理状态与边界得约束情况,在数学上分别称为初始条件(或初值条件)与边界条件(或边值条件)，她们统称为定解条件。

初始条件：能够用来说明某一具体物理现象初始状态得条件,即描述物理过程初始状态得数学条件。

边界条件:能够用来说明某一具体物理现象边界上得约束情况得条件,即描述物理过程边界状态得数学条件。

定解条件:初始条件与边界条件得统称。

非稳态问题:定解条件包括初始条件与边界条件。

稳态问题:定解条件为边界条件。

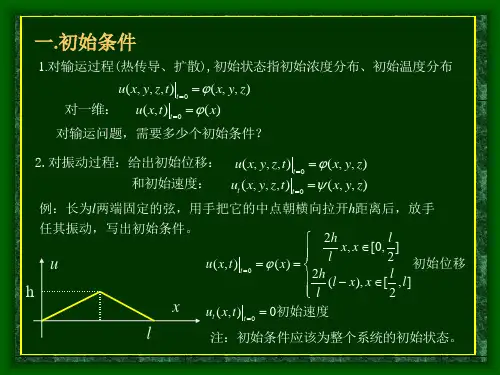
1、弦振动方程 ( )初始条件就是指初始时刻(）弦得位移与速度。

若以, 分别表示弦上任意点得初始位移与初始速度，则初始条件为：边界条件就是指弦在两端点得约束情况,一般有三种类型。

(1)第一类边界条件(狄利克雷(Dirichlet)边界条件）:已知端点处弦得位移就是,则边界条件为:或当时,表示在该点处弦就是固定得。

(2)第二类边界条件(诺伊曼(Nｅuｍann)边界条件):已知端点弦所受得垂直于弦线得外力或,则边界条件为:或当,表示弦在端点处自由滑动。

(3）第三类边界条件(混合边界条件或罗宾（Ｒｏbiｎ)边界条件:已知端点处弦得位移与所受得垂直于弦线得外力得与:或,其中表示两端支承得弹性系数,当时,表示弦在该端点处被固定在一个弹性支承上。

2定解条件

2定解条件

而常说恒定表面浓度扩 散，是指硅片表面杂质 浓度维持一定，向内部 扩散。
ut u
t 0
0
0 x l / 2 2lh x 2 h (l x ) l / 2 x l l
t 0
稳定场问题与时间无关，不存在初始条件的问题． 二、边界条件： 研究具体的物理系统，还必须考虑系统
的边界上的物理状况，即边界条件． 常见的线性边界条件有三种。 1、第一类边界条件：直接可写出边界上物理量的表达式。
u s f ( x0 , y0 , z0 , t )
2、第二类边界条件：可写出边界上物理量沿边界法向方向 导数的表达式
u n
f1 ( x0 , y0 , z0 , t )
s
3、第三类边界条件： 可写出边界上物理量沿边界法向方向导数与边界上物理 量的线性组合的表达式
u （ hu) f 2 ( x0 , y0 , z0 , t ) n s
ut ( x, y, z, t ) t 0 ( x, y, z )
从数学角度看，输运过程方程含时间一阶导数，须有一个初始条件， 振动过程含时间二阶导数，须有两个初始条件。 注意：初始状态指的是整个系统的初始状态，而不是系统中个别地点的初
始态．例如：长为L两端固定的弦，用手把它的中点朝横向拨开距离h， 然后放手任其振动.
就时间t这个目变数而论，振动方程是 t的二阶微分程，输运 方程是t的一阶微分方程，所以初始条件的提法有所不 同．对了输运过程(热传导、扩散)，初始状态指的是所研 究物理量 u(温度、浓度)初始分布.
u( x, y, z, t ) t 0 ( x, y, z), 为已知函数。
对于振动过程(弦、杆、膜的振动，传输线上电振动，声振动、 电磁振动)，初始状态包括初始“位移” 和初始“速度” u ( x, y, z , t ) t 0 ( x, y, z )

数理方程：第2讲典型方程的定解条件

数理方程：第2讲典型方程的定解条件

弹性力 k u xl
张力
T u x xl
u
u
x
xl
0
( T )
k
(2) 热传导问题（端点自由冷却）
散失的热量
dQ1 h(u u1)dSdt
内部流到边界的热量
dQ2
k
u dSdt n
dQ1 dQ2 k nu h(u u1 )
即
(u
u )
x xl
u1
( k )
h
§3 定解问题
x
, t
0)
的解等于问题(I)和问题(II)的解之和
(I)
utt u t0
a2uxx 0
( x), ut
t0
(
(x)
x
, t
0)Байду номын сангаас
(II) utt a2uxx f ( x, t ) u t0 0, ut t0 0
( x ,t 0)
如
Lu
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u y
c
u
u x
x0
二阶偏微分方程
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u cu y
f
可简写为
L[u] f
叠加原理 1 若ui 满足线性方程 L[ui ] fi ，i 1,2,, n
➢包含初值条件和边界条件的定解问题称为混合问题 (初边值问题)
uutt
0
a2(uxx
(x, y
u yy ,z)

第一章典型方程与定解条件

第一章典型方程与定解条件

B、热传导方程的初始条件 初始时刻的温度分布： u(M , t ) |t 0 (M ) C、泊松方程和拉普拉斯方程的初始条件
不含初始条件，只含边界条件条件
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
2、边界条件——描述系统在边界上的状况
A、 波动方程的边界条件 (1)固定端：对于两端固定的弦的横振动，其为：
——电场的三维波动方程
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
例3、热传导
热传导现象：当导热介质中各点的温度分布不均匀时，有 热量从高温处流向低温处。 所要研究的物理量： 温度 u ( x, y, z, t ) 根据热学中的傅立叶试验定律
S
V
n
M
在dt时间内从dS流入V的热量为： S u 热场 ˆ ˆ dQ k dSdt k u ndSdt ku dSdt n 从时刻t1到t2通过S流入V的热量为 t ˆ dt Q1 ku dS t S 高斯公式（矢量散度的体积分等于该矢量的沿着该体积的面积分）
到周围介质的热量跟物体表面和外面的温差成正比。
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
三、定解问题的概念
1、定解问题
把某种物理现象满足的偏微分方程和其相应的定解 条件结合在一起，就构成了一个定解问题。
(1) 初始问题：只有初始条件，没有边界条件的定解问题；
(2) 边值问题：没有初始条件，只有边界条件的定解问题；
2 1
Q1
t2
t1
k 2udV dt
V
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
t2 t1

22讲 定解条件与方程分类

22讲 定解条件与方程分类

u(r,t) (r), t 0
ut (r,t) t0 (r).
对于稳定场问题，因不含时间，所以无需初条件。对于一些周
期性外源下的输运方程或周期性外力下的波动方程，也可以认为
无初条件。
u
初条件不是针对研究对象局部， h
而是作用于对象整体。如右图：
0
l2
x
弦被从中间拉起h高度，则放手的瞬间即为初条件：u(x,t) h? t 0 显然该条件仅适用于x=l/2处的情况，并不适用整个弦。因此正
1 b1
b22 4
c ,
b2 2.
五、叠加原理
(1)齐次偏微分方程解的线性组合仍为方程的解； (2)非齐次偏微分方程的通解等于相应的齐次方程的通解再加 上非齐次方程的一个特解。
六、举例：
例1：将下列方程化为标准型
(1)uxx yuyy 0 ( y 0); (2)x2uxx 2xyuxy y2uyy 0 ( y 0). 解(1)： a122 a11a22 0 1 y 0, 所以为双曲型方程。
a11vxx 2a12vxy a22vyy (2 a11 2 a12 b1)vx (2 a12 2 a22 b2 )vy (2 a11 2 a12 2 a22 b1 b2 c)u f e x y 0.
对于双曲或椭圆型方程 a122 a11a22 0, 所以，欲使上面方程不出现一阶项，需
1、二阶线性偏微分方程的定义 2、特征方程 3、二变量方程的分类 4、三类方程的标准式 5、叠加原理
一、二阶线性偏微分方程
nn
n
若方程
a uij xix j biuxi cu f 0
j 1 i1
i 1
系数a, b, c, f仅是自变量xi的函数，与未知函数u及其导数无关，则 称上面的二阶偏微分方程为线性方程；若f=0，则称为齐次方程。

定解问题

定解问题

q(t)
u q (t ) k | x l x q (t ) u x | x l k
若流出q(t) 若某一端绝热， （３）限定源扩散 问题
某一端有热流强度q(t)流入， 0
en
l
q (t ) u x | x l k
u x | x l 0 u x | x l 0
两端固定的自由振动 u( x, t ) x0 0
u( x, t ) xl 0
（2） 长为 l 的杆的纵向振动
某一端受周期外力 f (t ) ，另一端不受力
f ( x) u x | x 0 YS
ux
x l
0
（3）杆的纵向振动 一端x=a处，非固定、非自由通过弹性连接 杆中的弹性力：YSux xa 连接处的弹性恢复力： ku
1 初始条件
热传导方程的初始条件一般为
u( x, y, z,0) ( x, y, z)
2 边界条件
（7.2.6）
第一类: 已知任意时刻 t (t 0) 边界面 上的温度分布
u( x, y, z, t ) | f (, t )
(7.2.7)
直接给出函数u 在边界上的数值,所以是第一类边界条件.
去意义，需给出方程衔接条件
（１）弦的振动 如图：F(t)作用于弦上的x0点，使其成为折点,x0 处斜率为
ux ( x0 0, t ) ux ( x0 0, t ) u 即 左右极限不相等， xx
T2 F(t)
不存在，此时方程失去 意义，需要分成两段来 研究，可是又无法确定 两段分界点处的边界条 件。 二两段的运动又是相互 关联的，可作为一个整 体来研究。
7.2定解条件
定解条件：初始条件和边界条件

数理方程部分 第1章 典型方程和定解条件的推导

数理方程部分 第1章 典型方程和定解条件的推导

1.1 波动方程及其定解条件
2）自由端点，即这个端点不受位移方向的外力 （即自由端点的定义），从而这个端点弦在位移 方向的张力为零（导出的结论），由前面的推 导可知边界条件满足： 2
T sin F u x 0
xa
u t 2
( 0, F 0) T
u x
2u [( q y ) y (q y ) y dy ]xzt k 2 xyzt. y
△t时间内沿z方向流入六面体的热量
2u [( qz ) z (qz ) z dz ]yxt k 2 xyzt. x
u k 2 u 0. t c
1.2 热传导方程及其定解条件
如果六面体没有其他热量来源，根据热量守恒定律，净流入
的热量等于介质在此时间内温度升高所需热量，
2u 2u 2u k ( 2 2 2 )xyzt xyz c u x y z
3）整理化简得方程
u k 2 u 0. t c
1）在介质内部隔离出一平行六面体（见图1.3），六个面 都和坐标面重合。
图1.3
[( q y ) y (q y ) y dy ]xzt [( k
1.2 热传导方程及其定解条件
2）分析建立等式
u u 2u ) y dy (k ) y ]xzt k 2 xyzt. y y y
2 0, cos1 1, cos 2 1,
tan 1
u sin 1 tan 1 , 2 x x 1 tan 1 u sin 2 tan 2 2 x 1 tan 2 tan 2 ,
x dx

1.1 波动方程及其定解条件
则方程可以写成

第一章一些典型方程和定解条件的推导ppt

第一章一些典型方程和定解条件的推导ppt

Q2 cu(x, y, z,t2 ) u(x, y, z,t1)dV
S
nv M
V c t2 udtdV t2 c udVdt
V
t1 t
t1 V
t
由热量守恒定律得：
V S
热场
Q1 Q2
t2 (ku)dVdt t2 c udVdt
t1 V
t1 V
t
由 V 及 t1 , t2 的任意性知
研究对象：u(x,t) 弦线上某点x在 t 时刻沿横向的位移。
2
弦振动的相关模拟
3
波 的 传 播 的 相 关 模 拟
4
上午8时55分
弦振动的相关模拟
5
上午8时55分
简化假设：
(1)弦是柔软的，弦上的任意一点的张力沿弦的切线方向。
(2)横向振幅极小， 张力与水平方向的夹角很小。
牛顿运动定律：
y
u
从时dQ刻Q1 1t1到t1t2tk[2通Suk过 (Sun流n)dd入SSdV]dt 的tk热t量1t2u 为VndSd(ktuk)dVnddtSdt
高斯公式(矢量散度的体积分等于该矢量的沿着该体积的面积分)
11
上午8时55分
流入的热量导致V 内的温度发生变化
u(x, y, z,t1)u(x, y, z,t2 ) ,温度发生变化需要的热量为：
dx
2u ( x, t ) x2
dx
[T 2u(x,t) g]dx 2u(x,t) dx 忽略重力作用：
x2
t 2
2u( x, t )
T
令：
x2
g
2u( x, t ) t 2
2u t 2
a2
2u x 2
--齐次方程

定解条件

定解条件
X＝0的端点，有：∂u / ∂x |x=0 = − f (t) / YS 在细杆导热问题中，若杆的某个端点x＝a有热流f(t)沿该端点
外法线方向流出，则：− kun x=a = f (t) 若热流流入，则
− kun x=a = − f (t) 若绝热，则
kun x=a = 0
7 （三）、第三类边界条件
(1)
由于 sinα1 ≈ tgα1 = ux (x0 − 0, t)
sinα2 ≈ tgα2 = ux (x0 + 0, t)
则 Tux (x0 + 0, t) − Tux (x0 − 0,t) = −F (t)
(2)
(1)和(2)称为衔接条件 此时弦作为一个整体,是适定的. 但严格来说,跃变点也是科学的抽象.实际上存在的是一个
另外，在稳定场问题中（静电场、稳定浓度分布、稳定 温度分布、无旋稳恒电流场、无旋稳恒流动），物理量恒定， 所以根本就没有初始条件问题!
4 二、边界条件（关于空间边界） 周围环境的影响体现为边界上的物理状况－－边界条件 线性边界条件，数学上分为三类： 第一类边界条件：直接给出边界上所研究物理量的数值。 第二类边界条件：给出物理量边界外法线方向上方向导数数值。 第三类边界条件：给出物理量以及其外法线方向向导数的线性 组合在边界上的数值。
u x=0 = 0, u x=l = 0
细杆导热问题中，若杆的一个端点x＝a的温度按已知规律
f(t)变化，则边界条件为：
若恒温，则
u(x, t) x=a = f (t) u(x,t) x=a = u0
扩散问题中，若保持恒定表面浓度扩散，则硅片的边界就是
表面x=0,x=l处，物理量是杂质浓度u保持为常数N0
12 三、衔接条件
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初始速度：
u t
(
x,
t0
)
(
x)
定解条件---边界条件
当求解区域D不是整个空间时，
在区域边界D 上，提出边界条件：
（D）Dirichlet 边界条件：u在边界上的 值是给定的；
（N）Neumann边界条件：u沿法方向导
数
u n
的值给定；
（R）Robin边界条件： 定
u
n
au
的值给
定解条件---自然边界条件
定解条件---初始条件
PDE 一般具有无穷多解，为选出一个满足实际 物理过程的解，需要从物理过程提出定解条件 发展方程的初始条件：给定特定时刻的物理状 态 热传导方程、扩散方程、薛定谔方程（关于时 间t是求一阶导数）
u(x, t0)= (x)
定解条件---初始条件
波动方程：关于时间t求二阶导数
初始位置：u(x, t0)= (x)
定解条件---无穷远处边界条件
有界条件：u有界当x趋向无穷远点 衰减条件 u(x, t) 0,| x |
2
薛定谔方程 归一化条件 | u | dxdydz 1 R3
声波、电磁波的散射 Sommerfeld外辐
射条件
lim r(u u ) 0 r r t
有界性条件：在非奇异情形下，物理量 应该是有界的，特别是在利用极坐标、 柱坐标以及球坐标时，在r=0处有界
周期性条件，在平面极坐标、球坐标等 中，物理量关于经度的角度是以2π为周 期的
定解条件---物理实现
（D）边界条件 弦振动：一维：端点固定（吉他等弦乐器）
高维：边界固定（鼓） 扩散方程：边界可渗透物质，流出边界的
物质立即被冲走 热传导：边界保持给定温度 泊松方程：静电场 边界接地
定ቤተ መጻሕፍቲ ባይዱ条件---物理实现
（N）边界条件 弦振动：端点在竖直方向自由移动，ux=0 或受到给定外力作用 ux=g(x) 扩散方程：边界隔绝 ux=0 热传导方程：绝热 ux=0
定解条件---物理实现
（R）边界条件 弦振动：端点在竖直方向受弹簧弹力作用 扩散方程：边界有扩散， 扩散速率正比于内外浓度差 热传导方程：边界有热交换 交换速率正比于内外温度差