当前位置：文档之家 › 5.10振动之互相垂直的简谐振动的合成(动画)

5.10振动之互相垂直的简谐振动的合成(动画)

  • 格式：pdf
  • 大小：7.64 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

2、简谐振动的合成

2、简谐振动的合成

A A1 A2
x
x1 A1 cos t x2 A2 cos(ωt π ) x x ( A2 A1 ) cos(ωt π)
o 2
A 2
A1
o
T
t
A
1) 相位相同 φ2 φ1 或 Δφ φ2 φ1 0
A A1 A2
相互加强
x A cos( t 1 ) A cos( t 2 ) 2) 相位相反 Δφ φ2 φ1 π
此结论对讨论各种波的干射、衍射极为有用。
二、 两个同方向不同频率简谐振动的合成 x1 A1 cos 1t A1 cos 2 π 1t
x2 A2 cos 2t A2 cos 2 π 2t
讨论 A1 A2 ,
x x1 x2
2 1 1 2 的情况
x y 2 1 2 A1 A2
π y A2 cos( t ) 2 0 质点沿顺时针方向运动
2 2
y
A1
A2
o
x
A2 y

x A1 cos t
o
A1
x
2 质点沿逆时针方向运动
用 旋 转 矢 量 描 绘 振 动 合 成 图
两 相 互 简 垂 振 直 动 同 的 频 合 率、 成 不 图 同 相 位
1 1 可见 π ( 2 1 )T拍 ∴ T拍 2 1 拍
拍 2 1
拍频（振幅变化的频率）
注意:书上的拍频写成，此处的拍频写成拍
2 1 1 2
( 1 2 ) / 2 1 2 , 1 2
(C)
3k / m /( 2π )

高二物理竞赛相互垂直的简谐运动的合成课件

高二物理竞赛相互垂直的简谐运动的合成课件

A A AA 例1：一轻弹簧在 60 N 的拉力下伸1长 30 cm。 2
12
对B球用牛顿第二定律得：
结论：频率较大而频率之差很小的两个同方向简谐运动的合成，其合振动的振幅时而加强时而减弱的现象叫拍
x y x y 又， A = 10 cm = 0.
2
( ) 0 0 简谐运动的运动学方程：
y 3 = 200 N/m
注意：
y +A2
若 t = 0 时，y = 0，则 x 为极
大值；
x
然后 x 向负向运动，而 y 则 -A1 O
+A1
向正极大值运动。
左旋椭圆
-A2
(5) 2 1等于其他值
表明：质点的轨迹是一个一般的椭圆。
y +A2
x
-A1
O
+A1
-A2
本章总结
本章主要介绍了简谐运动，以及振动的合成。
∴ 振动方程
(SI)
(5)
等于其他值
主要知识点： 3 = 200 N/m
(3)
，表明 x 落后于 y 为 。
(3) 物体从第一次越过平衡位置时刻起到它运动到上方 5cm 处所需要的最短时间。
对B球用牛顿第二定律得：
1. 简谐运动的运动学方程： 受迫振动：当驱动力频率与系统的固有频率相
例1：一轻弹簧在 60 N 的拉力下伸长 30 cm。
若 t = 0 时，y = 0，则 x 为极大值； 3 = 200 N/m
x
若 t = 0 时，y = 0，则 x 为极大值；
mg 4 10 然后 y 向负向运动，而 x 则向正极大值运动。 m k g x x 0 .2 m 例051m：)时一，轻由弹于簧弹在簧60对N物的体拉施力加下的0 伸拉长力3：0 cm。 0 k 200 等时发生共振现象。

同一直线上简谐振动的合成 相互垂直的简谐振动的合成 谐振分析 相空间中振动的轨道

同一直线上简谐振动的合成 相互垂直的简谐振动的合成 谐振分析 相空间中振动的轨道

A = A12 + A2 2 = 0.052 + 0.062 = 0.0781
A1 sin ϕ1 + A2 sin ϕ2 π ϕ = arctg( ) = arctg11 = 840 48′ A1 cos ϕ1 + A2 cos ϕ 6
3π x 1 = 0 .05 cos( 10 t + ) 4 1 x 2 = 0 .06 cos( 10 t + π ) 4
y A2
0
消去t得轨道方程
x 2 y 2 2 xy + 2− cos( 2 − ϕ1 ) = sin2 (ϕ 2 − ϕ1 ) ϕ 2 A1 A2 A1 A2
x A1
这是椭圆方程，质点的轨迹一 般是个斜椭圆。
x2 y2 2 xy + 2 − cos(ϕ 2 − ϕ 1 ) = sin 2 (ϕ 2 − ϕ 1 ) A12 A2 A1 A2
x 2 = 0 . 0 3 co s( 2 t − π / 6 )
求：合振动的表达式。
解：
A = A12 + A22 + 2 A1 A2 cos(ϕ 2 − ϕ 1 )
A = 0.04 2 + 0.03 2 + 2 × 0.04 × 0.03 cos( −π / 6 − π / 6 ) ≈ 0.06
= A1 cos(ω t + ϕ1 ) + A2 cos(ω t + ϕ 2 ) = A cos( ω t + ϕ )
其中
x = x1 + x2
x1 = A1 cos( ω t + ϕ 1 ) x 2 = A2 cos( ω t + ϕ 2 )
A = A1 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ 1 )

谐振动的合成课件

谐振动的合成课件
总结词：理论模型复杂化
详细描述：多摆的合成需要建立更为 复杂的理论模型，以准确描述各个摆 之间的相互作用和合成效果。
合成后的振动可以表现出不同 的振动特性，如频率、相位和 振幅等。
在本实验中，我们将利用信号 发生器和示波器来观察不同频 率、相位和振幅的谐振动的合 成效果。
实验步骤
步骤一
准备实验器材，包括 信号发生器、示波器 和实验平台。
步骤二
将信号发生器与示波 器连接，并调整信号 发生器输出不同频率 、相位和振幅的正弦 波信号。
。
06
谐振动的合成案例分析
单摆的合成案例
在此添加您的文本17字
总结词：简单直观
在此添加您的文本16字
详细描述：单摆是最简单的谐振动合成案例，通过观察单 摆的运动轨迹，可以直观地理解谐振动的合成原理。
在此添加您的文本16字
总结词：易于实现
在此添加您的文本16字
详细描述：单摆的合成实验装置相对简单，易于搭建和操 作，适合作为演示实验。
谐振动的合成原理
01
02
03
振动合成
将两个或多个振动源的振 动叠加起来，形成一个新 的振动。
振动叠加原理
线性振动系统中，多个振 动源引起的位移、速度和 加速度可以分别线性相加 。
谐振动的合成
将两个或多个简谐振动合 成，得到新的简谐振动。
谐振动的合成方法
相位差法
根据简谐振动的相位差， 确定合成振动的振动方向 和强度。
、滤波、频谱分析等。
离散傅里叶变换
离散傅里叶变换（DFT）是一种将离散时域信号转换为频域信号的数学 工具，通过对离散时间序列进行傅里叶变换，可以得到每个频率分量的 幅度和相位。
DFT的数学表达式为：X[k] = Σ[x[n]*e^(-i*2πkn/N)]，其中x[n]是离散 时间序列，N是序列长度，k是频率分量索引。

§11-4相互垂直的简谐振动的合成

§11-4相互垂直的简谐振动的合成

x
20 10 π 2
20 10 π 2
合振动运动轨迹为园
二、两个频率不同的相互垂直的简谐振动的合成
两个频率不同的相互垂直的简谐振动合成之后运动轨迹 随时间变化，不是稳定曲线。
1.频率相差很小，合运动轨迹缓慢变化。
2.频率相差较大，数值有简单的整数比值关系时，运动轨迹
为闭合曲线，称为李萨如图形。
y A2 x A1
合振动运动轨迹为直线
2、 20 10 π
y A2 x A1
合振动运动轨迹为直线
y
A2
A1 x
y
x A2
o A1
3、20 10 π 2
x2 A12

y2 A22
1
合振动运动轨迹为正椭圆
4、 两个简谐振动振幅相同时 y
A2 y
o A1 x
y
x
10 )
两个频率相同的相互垂直的简谐振动的合成为椭圆
椭圆的形状由两个振动的初相位差 20 决1定0
用旋转矢量描绘振动合成动画
两个频率相同的相互垂直的简谐振动的合成为椭圆
当初相位差不同时两个沿垂直方向的同频简谐振动的合成
或
讨论几种特殊情形 1、20 10 0 或 2 π
如图所示，图中所描绘的是
yA
x :y=3:2， 2 0= 0， 10 = /4 时的
李萨如图形。
图形与y轴切点数 图形与x轴切点数
-A2
nቤተ መጻሕፍቲ ባይዱ x 3 nx y 2
1
x
o
A2
- A1
不同频率比不同初相位差的李萨如图
在电子技术中常用李萨如图测定未知频率
完
第二篇

简谐振动简谐振动的合成课件

简谐振动简谐振动的合成课件

1、细线质量不计
约 定 2、 50 sin
0
3、阻力不计
M m glsin m gl 质点 m 受力如图重力矩： 波动：振动的传播（振动状态的传播）
弹性介质:是指由弹性力组合的连续介质。
二、超声波与次声波及其生物效应
相互垂直的简谐振动的合成
l 根据质点的动量距定理 （2）t =T/4 时，质点的位置、速度、加速度；
• •代数方法：设两个振动具有相同频率，
同一直线上运动，有不同的振幅和初相位
x1(t) A1 cos(t 1)
的仍 简然
x2(t) A2 cos(t 2)
x(t) x1(t) x2(t)
谐是 振同 动频
( A1 cos1 A2 cos2 ) cost。 率
( A1 sin1 A2 sin2 ) sint
质量可忽略的弹簧，一端固定，一端系一有质量的物体，称此系统为弹簧振子。
Ep
xA
X
波传播一个波长的距离所需时间
0
317.
13
1440
（2）波谷经过原点的时刻
（3）第一次通过平衡位置的时刻。
E
与地球、海洋及大气的大规模运动有关。
0
331.
E p Ek
t
x
胡玉才：e-mail
五、阻尼振动 受迫振动 共振
用李萨如图形 在无线电技术 中可以测量频 率：
Tx :Ty 1: 2
在示波器上，垂直方向与水平方向同时 输入两个振动，已知其中一个频率，则 可根据所成图形与已知标准的李萨如图 形去比较，就可得知另一个未知的频率。
0
几幅典型的利萨如图形
1:2
1:3
2:3
2
x :y 2 :1 2

简谐振动、振动合成ppt课件

简谐振动、振动合成ppt课件

x0
A0
-A 0
A
0
0 -A 0
A 0
;
9
5、振幅与初相的确定
初始条件：x t0 x0 , V t0 V0
x A cos(t ) v A sin( t )
x0 A cos ① v0 A sin ②
①2+(②/)2
有
x
2 0
(v0
/ )2
A2
A
x02
v0
2
②/①有
tg v0 / A v0
A M
A v t M 0
2. M 点的运动速度
ox P x
v A
在 x 轴上投影速度
v A sin( t )
;
31
3. M 点的加速度
a A2
在x轴上投影加速度
a A2 cos(t )
y
aM
A M A2 t 0
ox P x
结论：
M点运动在x轴投影，为谐振动的运动方程。
M点速度在x轴投影，为谐振动的速度。
x
14
建立坐标系，o点选在弹簧平衡位置处。
F弹 x
3.振动位移
ox
振动位移：从 o 点指向物体所在位置的矢量。
回复力： 一维振动
F弹 k x F弹 kx ma
a d 2x F弹 k x
dt 2 m;
m
15
d2x k x 0 dt 2 m
F弹 x
令
2 k
m
ox
有
d 2x 2x 0 简谐振动微分方程
2
1 mA 2 2 sin 2 (t )
2
;
25
Ek
1 m 2 A 2 sin

5垂直方向简谐运动的合成 -

5垂直方向简谐运动的合成 -
A2 斜率 A1
y
x
质点离开平衡位置的位移
S x y
2 2
A1 A2 cos( t )
2 2
x2 y2 x y 2 2 cos( ) sin ( 20 10 ) 20 10 2 2 A1 A2 A1 A2
x y 2 (2) 20 10 ( ) 0 A1 A2
A2 y x A1
合振动的轨迹为通过原点且 在第二、第四象限内的直线
A2 斜率 A1
y
x
质点离开平衡位置的位移
S x y
2 2
A1 A2 cos( t )
2 2
x2 y2 x y 2 2 cos( ) sin ( 20 10 ) 20 10 2 2 A1 A2 A1 A2
(3) 20 10

2
x2 y2 1 A1 A2
合振动的轨迹为以x轴和y轴 为轴线的椭圆
x A1 cos( t 10 )
y A1 cos( t 10
y
x

2
)
质点沿椭圆的运动方向是顺时针(右旋)的。
x2 y2 x y 2 2 cos( ) sin ( 20 10 ) 20 10 2 2 A1 A2 A1 A2
x2 y2 x y 2 2 cos( ) sin ( 20 10 ) 20 10 2 2 A1 A2 A1 A2
讨论
x y 2 ) 0 (1) 20 10 0 ( A1 A2
A2 y x A1
合振动的轨迹为通过原点且 在第一、第三象限内的直线
1
两振动的频率成整数比 轨迹称为李萨如图形

相互垂直简谐运动合成

相互垂直简谐运动合成

A1A 2
2
1
2 2 1
2 1 4
斜椭圆方程
x2 A2
1
y2 m A22
xy 2
AA 12
1 2
2 1 4
2
1
74
4
顺时针 逆时针
相互垂直的简谐运动的合成
2
1
3
4
x2 y2 A12 A22
2 xy 1 斜椭圆方程 A1A 2 2
2 1 3 4
顺时针
2
1
5434
逆时针
一般情况21====任意值任意值任意值任
意值,,都为椭圆方程都为椭圆方程都为椭 圆方程都为椭圆 方程..
相互垂直的简谐运动的合成
二、两个不同频率相互垂直简谐运动的合成 李萨如图形（Lissajou figure）
一般情况下, 合振动的轨迹是不稳定的. 当两个分振动 的频率成简单整数比时, 将形成稳定闭合曲线.
相互垂直的简谐运动的合成
不同频率相互垂直的简谐运动的合成
x A1 cost1 1 y A2 cost2 2
任意时刻 t::由坐标由坐标(x，y)确定质点的
位 置.确定质点的位置确定质点的位置确
定质点Ax22的 1
Ay位222 置 )y，A2，1xA，yx(由2 c坐os标由2 坐1标消si去n 2
t得2 (1
推导从略)
——轨迹方程（椭圆方程）
相互垂直的简谐运动的合成
大学物理
振动学基础
第8讲 相互垂直的简谐运动的合成
相互垂直的简谐运动的合成
相互垂直的简谐运动的合成
激光李萨如图形演示 两个相互垂直简谐运动的合运动仍是简谐运动吗?
相互垂直的简谐运动的合成

振动之互相垂直的简谐振动的合成(动画)

振动之互相垂直的简谐振动的合成(动画)
[解析](3)当两个分振动的频率不同 时，质点轨迹的参数方程为 x = A1cos(ω1t + φ1)，y = A2cos(ω2t + φ2)
当频率或周期构成简单的整数比且初位 相之差恒定时，质点的轨迹是一条稳定 的闭合曲线，这种曲线叫做李萨如图形。
x方向周期和 y方向周期之 比是1：1。
取x振动 的初相为 零，取y 振动的初 相为φ， 这也是两 个振动的 相差。
当相差为π时， 质点的轨迹是 反“S”形。
当两个子图的相差满足Δφ + Δφ‘= 2π时(Δφ = 0 的情况除外)时，轨迹相同而运动方向相反。
当两个振动的周期互质时，取它们的乘积为质点运动时间， 那么质点都可以运动若干个完整的周期，最后回到起点。
相差为0与 相差为π的 轨迹和质 点的运动 方向是相 同的，相 差为π/8和 7π/8的轨 迹相同， 但是质点 的起点和 运动方向 不同。
(2)一个质点同时参加两个互相垂直的频率相近的简谐振 动，质点运动的轨迹是什么？
[解析](2)当两个分振动的频率不 同时，质点轨迹的参数方程为
x = A1cos(ω1t + φ1)，y = A2cos(ω2t + φ2)
参数为时间t，ω2 = ω1 + Δω，Δω很小。
质点运 动的轨 迹交织 在一起， 就象网 格一样。
即 s A12 A22 cos(t 1)
合振动也是简谐振动，频率和位相与分振动相同，振幅为
②当φ2 - φ1 = (2k + 1)π时(k为整 数)，即两个振动反相，可得
y A2 x, A1
A12 A22
质点的运动轨迹是一条通过原点的斜率为-A2/A1的直线。
合振动也是简谐振动，频率和相位与分振动相同，振幅相同。

相互垂直的简谐振动的合成

相互垂直的简谐振动的合成

相互垂直的简谐振动的合成简谐振动是一种重要的物理现象，在许多领域都有广泛的应用，如机械、光学、电磁等领域。

在某些情况下，需要对两个或更多相互垂直的简谐振动进行合成，以产生一个新的复合振动。

本文将介绍相互垂直的简谐振动的合成，并阐述其原理和应用。

简谐振动的定义简谐振动是指一个对象以一个周期性的方式在其平衡位置周围运动的物理现象。

这种振动是由于弹性力的作用而产生的，例如弹簧、摆线、声波等。

一个简谐振动的特点是在相同的时间内，运动具有相同的加速度和速度。

简谐振动的运动方程可以用以下公式表示：x = A sin(ωt)其中，x代表位移，A代表振幅，ω代表角速度，t代表时间。

由于简谐振动的周期（T）与角速度有关系，因此可以用以下公式表示：T = 2π/ω当存在两个或更多个以不同的频率振动的物体时，它们的振动将会互相影响。

考虑一个垂直向上运动的弹簧振子和一个水平运动的弹簧振子。

如果它们同时振动，将会出现一个垂直方向上的复合振动。

其中，y1代表第一个弹簧振子的位移，y2代表第二个弹簧振子的位移。

为了合成垂直方向的复合振动，需要执行以下步骤：1. 确定两个振动的振幅和角频率。

2. 计算两个振动的周期。

3. 将两个振幅和周期代入以下公式中：y = A1 sin(ω1t) + A2 sin(ω2t)其中，y代表合成振动的位移。

4. 对于每个时刻t，计算出合成振动的振幅y。

合成垂直方向振动的物理意义当两个垂直方向上的简谐振动相互作用时，它们的复合振动将形成一个网格图形，每个节点表示一个特定的振幅和相位差。

相位差表示两个振动之间的时间差，其中一个振动的周期相对于另一个振动周期的时间差。

合成振动的频率与原始简谐振动的差异通常很小，因此可以将它们看作共振现象。

在许多现实情况下，相互垂直的简谐振动产生的复合振动是非常有用的，例如在音乐和声学领域。

应用和例子1. 双摆双摆是指两个以不同长度的摆绳悬挂并以不同频率振动的摆。

当它们相互作用时，将产生一个复合振动，其中一个摆的振动会影响另一个摆的振动，并且它们最终会形成一个规律的图案。

第5节 互相垂直的简谐振动的合成

第5节 互相垂直的简谐振动的合成

第 5 节互相垂直的简谐振动的合成
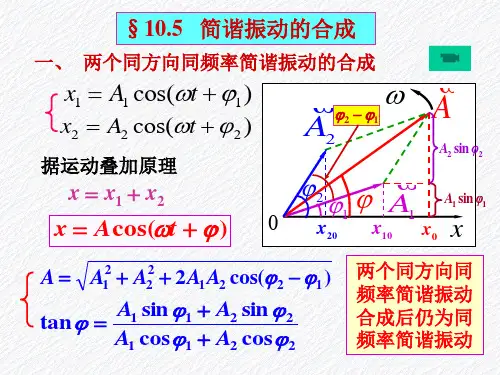
一、互相垂直的同频率的简谐振动的合成
1、合振动的特点
振动系统可以同时参与方向互相垂直的两个振动。

设一个振动沿 x 方向，一个沿 y 方向，即：
这组方程实际上就是合振动的坐标的参数方程。

2、合振动和分振动的关系
（1）若，则有：
合振动的轨迹为直线。

同理，若，有：
合振动轨迹仍为直线。

（2）若，则有：
合振动为椭圆，当时，轨迹为圆。

（3）一般情况
其中：
对于不同的，可得到不同形状、不同绕向的椭圆。

二、互相垂直不同频率的简谐振动的合成
如果两方向的振动频率不相等，它们的合振动为：
当和成整数比时，合振动的轨迹仍是一些闭合的曲线，称为李萨如图形。

当和不成整数比时，合振动的轨迹不再是闭合曲线，利用李萨如图形的性质，可以精确判断出两种频率是否成整数比，并根据已知频率确定未知频率。

物理-相互垂直的简谐运动的合成

物理-相互垂直的简谐运动的合成

y A2 x A1
质点离开 平衡位置 的位移
r(t) A12 A22 cos(t 1 )
y
A2
o A1 x
合振动是与分振动同频率的简谐振动
一、两个相互垂直的谐振动的合成
x A1
2
y A2
2
2xy cos(2 A1 A2
1 )
s in2 ( 2
1 )
(3)
若
2
1
2
x2 A12
y2 A22
合运动的 轨道方程
( x )2 ( y )2 2xycos sin2
A1
A2
A1 A2
其中： (2 1 )t (2 1 ) ——随时间变化
一般情况下，合运动的轨迹是不稳定的。
一、两个相互垂直的谐振动的合成
分振动： x A1 cos(ω1t φ1 ) y A2 cos(ω2t φ2 )
二、振动频谱分析
数学上已经证明：
任意周期函数（周期为T）：x(ωt) 其中 ω 2π /T
均可展开为三角级数
基频
x(ωt ) a0 (ak cos kωt bk sin kωt )
k 1
k次谐频
1 T/2
a0 T
f (ωt )dt
T / 2
2
ak T
T /2
f (ωt)cos kωtdt (k 0)
x A1
2
y A2
2
2xy cos(2
A1 A2
1 )
s in2 ( 2
1 )
合运动一般是在 x A1, y A2 范围内的一个椭圆。
一、两个相互垂直的谐振动的合成
2
2
x A1
y A2

两个互相垂直的简谐振动合成

两个互相垂直的简谐振动合成

拍的振幅为)cos(t A 2212 振幅的周期为121222)(T 拍频为122121T拍的振动曲线如右图三、两个互相垂直的简谐振动的合成两简谐振动为)cos( t A x （1）)cos( t B y （2）以cos 乘以(3)式，cos 乘以(4)式，后相减得改写为 sin sin cos cos t t A xsin sin cos cos t t By（3）（4）)sin(sin cos cos t ByA x （5）)(sin )cos( 222222ABxy B y A x 以sin 乘以(3)式，sin 乘以(4)式后相减得(5)式、(6)式分别平方后相加得合振动的轨迹方程)sin(cos sin sin t ByA x （6）医学物理学此式表明，两个互相垂直的、频率相同的简谐振动合成，其合振动的轨迹为一椭圆，而椭圆的形状决定于分振动的相位差（ － ）。

xA o -A-BB a b y 讨论：1. － 0 或 时02 )(B y A x 即x A B y 合振动的轨迹是通过坐标原点的直线，如图所示。

－ 0时，相位相同，取正号，斜率为B /A 。

－ 时，相位相反，取负号，斜率为-B /A 。

合振动的振幅22BA C医学物理学2. 当2时xAy B22221合振动的轨迹是以坐标轴为主轴的正椭圆，如右图所示。

－ = /2时，合振动沿顺时针方向进行；－ = /2时，合振动沿逆时针方向进行。

A =B ，椭圆变为正圆，如右图所示。

xAB o y-A-BxA A -A-Ay o医学物理学3.如果( )不是上述数值，那么合振动的轨迹为椭圆，其范围处于边长分别为2A (x 方向)和2B (y 方向)的矩形内。

两个分振动的频率相差较大，但有简单的整数比关系，合振动曲线称为利萨如图形。

04垂直简谐振动的合成

04垂直简谐振动的合成

相位差决定。 相位差决定。 •合运动一般是在 2A1 ( x向 )、2A2 ( y向 ) 范围内的一 合运动一般是在 向 、 向 个椭圆。 个椭圆。
x y 2xy cos(ϕ2 − ϕ1 ) 2 = sin (ϕ2 − ϕ1 ) + − A1 A2 A1 A2 上式是个椭圆方程， 上式是个椭圆方程，具体形状由 ∆ ϕ = ( ϕ 2 − ϕ 1 )
③ ④
③ cos ϕ 2 ④ cos ϕ1 − A1 A2
x cos ϕ 2 y cos ϕ1 − = sin ωt sin(ϕ 2 − ϕ1 ) ⑤ 得 A1 A2
13
x = A1 (cosωt cosϕ1 − sin ωt sin ϕ1 ) y = A2 (cosωt cosϕ2 − sin ωt sin ϕ2 )
14
7
∆ϕ = π / 4
y
8
1 2
y
8 7 6 5 5
4 4
7 6
2
1
x
3
3 3
2 1
4
播 放 动 画
5 6 7
x
8
8
播放动画
9
二、相互垂直不同频率简谐振动的合成
一般是复杂的运动，轨道不是封闭曲线， 一般是复杂的运动，轨道不是封闭曲线，即合成运 动不是周期性的运动。下面就两种简单情况讨论： 动不是周期性的运动。下面就两种简单情况讨论： 1. 两分振动频率相差很小
∆ϕ = (ω2 − ω1 )t + (ϕ2 − ϕ1 )
缓慢变化,合运动轨迹将 可看作两频率相等而 ∆ϕ 随 t 缓慢变化 合运动轨迹将 按下图依次缓慢变化 依次缓慢变化。 按下图依次缓慢变化。
∆ϕ = 0

相互垂直的简谐振动的合成ppt课件

相互垂直的简谐振动的合成ppt课件
1.频率相差很小，合运动轨迹缓慢变化。
2.频率相差较大，数值有简单的整数比值关系时，运动轨迹 为闭合曲线，称为李萨如图形。
y
x
A1
A2
o
-A2
- A1
如图所示，图中所描绘的是 x :y=3:2， 2 0= 0， 10 = /4 时的 李萨如图形。
图形与y轴切点数
图形与x轴切点数
不同频率比不同初相位差的李萨如图
2、
合振动运动轨迹为直线
合振动运动轨迹为直线
3、
4、 两个简谐振动振幅相同时
合振动运动轨迹为正椭圆
合振动运动轨迹为园
二、两个频率不同的相互垂直的简谐振动的合成
两个频率不同的相互垂直的简谐振动合成之后运动轨迹随时间变化，不是稳定曲线。
设一个质点同时参与两个相互垂直的同频率简谐振动
一、两个频率相同的相互垂直的简谐振动的合成
消去时间t得轨迹方程：
两个频率相同的相互垂直的简谐振动的合成为椭圆
椭圆的形状由两个振动的初相位差 决定
用旋转矢量描绘振动合成动画
两个频率相同的相互垂直的简谐振动的合成为椭圆
当初相位差不同时两个沿垂直方向的同频简谐振动的合成
在电子技术中常用李萨如图测定未知频率
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

{范例5.10} 互相垂直的简谐振动的合成(动画)
(1)一个质点同时参加两个互相垂直的频率相同的简谐 振动，讨论质点的合振动，观察质点运动的轨迹。 [讨论]
x 2 y 2 2 xy cos(ϕ 2 − ϕ1 ) sin 2 (ϕ 2 − ϕ1 ) + 2− = 2 A1 A2 A1 A2
③当φ2 - φ1 = π/2时，可得
当两个 互相垂 直的简 谐振动 的频率 有很小 差异时， 相位差 就不是 定值， 合振动 的轨道 在矩形 范围内 由直线 逐渐变 为椭圆， 再由椭 圆逐渐 变成直 线，并 重复进 行。
{范例5.10} 互相垂直的简谐振动的合成(动画)
(3)一个质点同时参加两个互相垂直的频率 相近的简谐振动，质点运动的轨迹是什么？ [解析](3)当两个分振动的频率不同 时，质点轨迹的参数方程为 x = A1cos(ω1t + φ1)，y = A2cos(ω2t + φ2) 当频率或周期构成简单的整数比且初位 相之差恒定时，质点的轨迹是一条稳定 的闭合曲线，这种曲线叫做李萨如图形。
(2)一个质点同时参加两个互相垂直的频率相近的简谐振 动，质点运动的轨迹是什么？ [解析](2)当两个分振动的频率不 同时，质点轨迹的参数方程为 x = A1cos(ω1t + φ1)，y = A2cos(ω2t + φ2) 参数为时间t，ω2 = ω1 + Δω，Δω很小。
质点运 动的轨 迹交织 在一起， 就象网 格一样。
相差为π/4和7π/4的 轨迹相同，但是质 点的起点和运动方 向不同。
当相差为π时， 质点的轨迹是 反“S”形。
当两个子图的相差满足Δφ + Δφ‘= 2π时(Δφ = 0 的情况除外)时，轨迹相同而运动方向相反。
当两个振动的周期互质时，取它们的乘积为质点运动时间， 那么质点都可以运动若干个完整的周期，最后回到起点。
质点的运动轨迹是一条通过原点的斜率为A2/A1的直线。 质点在任意时刻离开平衡位置的位移为
s= x2 + y 2 =
2 A12 cos 2 (ωt + ϕ1 ) + A2 cos 2 (ωt + ϕ 2 )
2 即 s =+ A2 cos(ωt + ϕ1 ) A12
合振动也是简谐振动，频率和位相与分振动相同，振幅为 A2 ②当φ2 - φ1 = (2k + 1)π时(k为整 2 y = − x, A12 + A2 数)，即两个振动反相，可得 A1 质点的运动轨迹是一条通过原点的斜率为-A2/A1的直线。 合振动也是简谐振动，频率和相位与分振动相同，振幅相同。
质点的运动轨迹和方向的分析与周期之比为1：4的情况相同。
如果周期 之比相反， 例பைடு நூலகம்2：1， 则质点运 动的轨迹 与周期之 比为1：2 的相同， 但是旋转 了90度。
MATLAB可视化 大学物理学
第五章结束 湖南大学物电院 周群益老师谢谢您的使用!
x2 y 2 + 2 = 当A1 = A2时，质 1 2 A1 A2 点轨迹就是圆。
质点的运动轨迹是以坐标轴为主轴的 椭圆，质点沿椭圆按顺时针方向运动。
反之，一个沿直线 的简谐振动，匀速 ④当φ2 - φ1 = -π/2或3π/2时，仍得相同 圆周运动和某些椭 的椭圆方程，但是质点运动方向相反。 圆运动，都可以分 ⑤当φ2 - φ1为其他值时，质点运动轨迹为斜 解成两个相互垂直 的简谐振动。 椭圆，其运动方向由相差φ2 - φ1决定。
相差为0与 相差为π的 轨迹和质 点的运动 方向是相 同的，相 差为π/8和 7π/8的轨 迹相同， 但是质点 的起点和 运动方向 不同。
当两个子图的相差满足Δφ + Δφ‘ = π时(Δφ = 0 的情况除外)时，轨迹相同而运动方向相反。
相差为0与 相差为π/2 的轨迹和 质点的运 动方向是 相同的， 相差为 π/16和 7π/16的轨 迹相同， 但是质点 的起点和 运动方向 不同。 当两个子图的相差满足Δφ + Δφ‘ = π/2时(Δφ = 0 的情况除外)时，轨迹相同而运动方向相反。
总之，两个相互垂直的同频率简谐振动合成时，合运 动一般是椭圆，质点运动方向由相位差φ2 - φ1决定。
相差为0和2π时，质点振动的轨迹和方向都是相同的。
两个子图的相差满足Δφ + Δφ' = 2π时(Δφ = 0或π的情况除 外)时，质点的轨迹是相同的，但是运动方向相反。
{范例5.10} 互相垂直的简谐振动的合成(动画)
{范例5.10} 互相垂直的简谐振动的合成(动画)
(1)一个质点同时参加两个互相垂直的频率相同的简谐振动， 讨论质点的合振动，观察质点运动的轨迹。(2)一个质点同 时参加两个互相垂直的频率相近的简谐振动，质点运动的 轨迹是什么？(3)如果两个简谐振动的频率或周期成简单的 整数比，质点运动的轨迹是什么？ [解析]设两个同频率的简谐振动分别沿x轴和y轴进行， 位移为x = A1cos(ωt + φ1)，y = A2cos(ωt + φ2)， 这就是质点运动的参数方程。 将余弦函数展开得 x/A1 = cosωtcosφ1 - sinωtsinφ1，y/A2 = cosωtcosφ2 - sinωtsinφ2 xsinφ2/A1 - ysinφ1/A2 = cosωtsin(φ2 - φ1) 可得 xcosφ2/A1 - ycosφ1/A2 = sinωtsin(φ2 - φ1) 质点的轨 这是椭 迹方程为 圆方程。 两个互相垂直的同频率简谐振动的合成一般是椭圆，其形状和 大小以及两个主轴的方向由振幅A1和A2以及初相差φ2 - φ1决定。
x方向周期和 y方向周期之 比是1：1。
取x振动 的初相为 零，取y 振动的初 相为φ， 这也是两 个振动的 相差。
相差为π/4的整数倍，9个子图就能将相差为0到2π的典型运动轨迹都 画出来，第一个子图(相差为0)与最后一个子图(相差为2π)是相同的。
当相差为0时，质 点在一条“S”形 曲线上来回运动。 一条“S”曲线实 际上是两条相同 曲线重叠的结果。
x 2 y 2 2 xy cos(ϕ 2 − ϕ1 ) sin 2 (ϕ 2 − ϕ1 ) + 2− = 2 A1 A2 A1 A2
{范例5.10} 互相垂直的简谐振动的合成(动画)
x 2 y 2 2 xy [讨论] cos(ϕ 2 − ϕ1 ) sin 2 (ϕ 2 − ϕ1 ) + 2− = 解得 2 A1 A2 A1 A2 A2 x 2 y 2 2 xy ①当φ2 - φ1 = 2kπ时(k为整数)， x + 2− = y= 0, 2 A1 A2 A1 A2 A1 即两个振动同相位，可得