当前位置：文档之家 › 两回转体表面相交

两回转体表面相交

  • 格式：docx
  • 大小：247.40 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

相贯的画法

相贯的画法
（四）相贯的画法
相贯---两立体（回转体）表面相交，其交线称为相贯线。 1、相贯线的性质：
共有性:相贯线是相交两立体表面的共有线，也是 两立体表面的分界线。 封闭性:由于立体均具有一定的范围，所以相贯线 一般由封闭的空间曲线。
相贯线的形状取决于立体的几 何性质、相对大小以及它们的相 对位置。
2、相贯线的作图方法： 辅助平面法———三面共点原理 原则： 要求辅助平面与立体表面交线的投影应为直线或圆.
PH
3、相贯线的简化画法
1´
2´
3’(4’)
1”(2”)
4”
3”
找特殊点; 作垂直平分线，得到圆心和半径。
4、相贯线的特殊情况
1）柱柱等直径相贯
2）有公共内切球--柱锥相贯
5、组合相贯线
例1
例2、两空心圆筒垂直相贯
本次课教学内容小结
教学主要内容： 用辅助平面法求相贯线
求相贯线的思路与方法： 由给定的视图分析相贯立体表面的几何性质、相贯两立 体的相对位置和大小、相贯两立体相对于投影面的位置；
相贯线的作图步骤:
(1)形体面的位置；
b´
(2)求相贯线上的特殊点
(3)求一系列中间点，选 正平面作为辅助面
(4)根据虚实性光滑连线
4’ 1’(2’)
2
3
4
b 1
Pw
3”4”
2”
b”
1”
PH
相贯线的作图步骤:
(1)形体分析
(2)求相贯线上的特殊点 (3)求一系列中间点 (4)根据虚实性光滑连线
分析相贯线可以通过何种辅助平面求出,要求辅助平面与 两立体表面的交线的投影分别是简单易画的图线-直线或 圆；
找出相贯线上的特殊点；

回转体表面相交(相贯线)

回转体表面相交(相贯线)

线的圆。当轴线平行
于某投影面时，这些 圆在该投影面上的投 影为直线段。
相贯线
三、两圆柱轴线平行
例: 补全正面投影
补全侧面投影。
例题：
已知被切割圆柱的主视图和俯视图，求左视图。
y1
y
y1
y
两轴线正交圆柱相贯线的趋势
动画
四、两圆柱相贯线的
常见情况：
b)
圆柱孔与实心圆柱相交
a) 两实心圆柱相交 c) 两圆柱孔相交
五、相贯线的特殊情况
1、两直径相等的圆柱
轴线相交成直角， 其相贯线是两个相 同的椭圆。 这两个椭圆的正面 投影是两条相交且 等长的直线段。
相贯线
2、两个同轴回转体 的相贯线是垂直于轴
动画
三、作图方法
例： 求作轴线垂直相交两圆柱的相贯线
1’ 4’ 3’ 2’ 4” 1” （2”） y y
3”
分析: 已知相贯线的 水平投影和侧面投影 求作：正面投影
作图步骤：
4
y 1 2 4 2 3
1、作特殊点 2、作一般位置点 3、柱）的轴线方向。
y
画出两轴线正交的圆柱孔的相贯线
§3-3
两回转体表面相交
相贯线：两立体相交时在表面上产生的交线。 一、 两回转体相交时的基本性质： 1、相贯线是两曲面立体表面的 共有线，相贯线上的点是两 曲面立体表面上的共有点。 2、两曲面立体的相贯线一般是 封闭的空间曲线，特殊情况 下可以是平面曲线或直线。
二、决定相贯线形状的相关因素
⒈ 取决于相交两曲面立 体的几何性质。 ⒉ 当它们的大小或相对 位置不同时，相贯线 的形状也随之而异。

5-3两回转体表面相交ccx

5-3两回转体表面相交ccx

轴 线 正 交
柱 锥 相 贯
§5-3 两回转体表面相交
本节结束
§5-3 两回转体表面相交
4
8
5
3
6
§5-3 两回转体表面相交
二、辅助平面法
两形体相贯线的形式有三种：
外外相贯、内内相贯、外内相贯
内相贯线 外相贯线
外相贯线
内相贯线
外相贯线
§5-3 两回转体表面相交
二、辅助平面法
两形体相贯时，如果两形体的形状、大小和相对位置均相 同，则无论相贯形式如何，相贯线的形状和作图方法都相同。
外外相贯
(1) 3
2
§5-3 两回转体表面相交
二、辅助平面法
例2 求四分之一的圆环面与圆柱面的交线。
R2W R1W 2' 5'(7') 3' (4') 1' 6'(8') 2” 4” 7” 8” 1” 5” 3” 6”
作图： (1)选辅助面(正平面); (2)判别并求出特殊点; (3)求中间点；
4 (1) 3
§5-3 两回转体表面相交
外内相贯
内内相贯
二、辅助平面法
例2 求四分之一的圆环面与圆柱面的交线。
共有点
共有点
§5-3 两回转体表面相交
二、辅助平面法
例2 求四分之一的圆环面与圆柱面的交线。
R1W 2' 3' 1' 4” 1” 2” 3”
作图： (1)选辅助面(正平面); (2)判别并求出特殊点;
3
§5-3 两回转体表面相交
二、辅助平面法
例1 求轴线正交的圆柱与圆台的相贯线。 作图：
RW
3”
1'

常用回转体相交的表面交线

常用回转体相交的表面交线

2 aY
1
b 6 RH
7
因为两圆柱旳水平投影 左右对称，侧面投影上下 对称。故相贯线旳正面投
旳同面投影依次光滑地连 接起来，即得相贯线。 4.补全外形线，完毕作图
影上下、左右对称。
返回
例6：求两轴线交叉圆柱旳相贯线 Y RW
3` 4` 2`
a`
5` 6` b`
1`
7`
4`` 3``
2``
(5``)
13
3
4
2
3 3
1 4 2
返回
1、相贯线旳性质
（1） 、一般情况下,相贯线为封闭旳空间曲线。 （2）、相贯线是两立体表面旳共有线，相贯线上旳点是 两立体表面旳共有点。
返回
2、相贯线旳三种基本形式
（1）、两外表面相交 （2）、外表面与内表面相交 （3）、两内表面相交
外表面和外表面相交 外表面和内表面相交
2``
2``
最终最低点投影
最 左
最 左
2
最最 右高
最 高
1
最点 高
点
点
投
2
投
影
影
最前最低点投影
最
前
1
最
2
低
点
圆柱圆锥相贯线
1`
1`
2`
（2）求一般点。
1``
2``
2``
2 1
2
Ⅲ
Ⅱ Ⅳ
Ⅰ
例4：求两轴线相交旳圆柱圆锥相贯线
（2）求一般点。
1`
1`
RV
1``
5`
6` 2`
2`` 4`` 5`` 2``
1 2
1 2
1
2

9两回转体表面相交

9两回转体表面相交

以大圆的半径为半径，从小圆的 以大圆的半径为半径 两边向大圆的中心弯
作业布置（ 作业布置（八） P14（ P14（2、3、） 曲面立体截交线 P15（ P15（3、4）
● ●
●
● ●
●
提示： 提示：
圆柱上的相贯 线，可以根据三个 用圆弧画出。 点，用圆弧画出。
利用“三面共点”的原理，通过求两曲面立体表 利用“三面共点”的原理，通过求两曲面立体表 辅助平面的一系列共有点，即可求出两曲面立体 的一系列共有点 面与辅助平面的一系列共有点，即可求出两曲面立体 表面的相贯线。 表面的相贯线。
空间及投影分析： 空间及投影分析： 作图方法
两圆柱相贯时，如果两形体的相贯形式相同， 两圆柱相贯时，如果两形体的相贯形式相同，则相贯 线的形状和作图方法都相同。 线的形状和作图方法都相同。
外相贯
外内相贯
内内相贯
★ 外形交线 两外表面相贯 内表面和一外表面相贯 ★ 内形交线 两内表面相贯
★ 外形交线 两外表面相贯 内表面和一外表面相贯 ★ 内形交线 两内表面相贯
空间及投影分析： 空间及投影分析： 作图方法
小圆柱轴线垂直于H面 小圆柱轴线垂直于 面，水 利用积聚性，采用表面定点法 利用积聚性 平投影积聚为圆， 平投影积聚为圆，根据相贯线的 首先找特殊点 ☆ 首先找特殊点 共有性， 共有性，相贯线的水平投影即为 该圆。大圆柱轴线垂直于W面 该圆。大圆柱轴线垂直于 面， ☆ 补充中间点 侧面投影积聚为圆， 侧面投影积聚为圆，相贯线的侧 ☆ 判断可见性，光滑连接 判断可见性， 面投影在该圆上。 面投影在该圆上。
三个或三个以上的立体相交，其表面形成的交线， 三个或三个以上的立体相交，其表面形成的交线，称为组 合相贯线。组合相贯线的各段相贯线， 合相贯线。组合相贯线的各段相贯线，分别是两个立体表面的 交线，而两段相贯线的连接点， 交线，而两段相贯线的连接点，则必定是相贯体上的三个表面 的共有点。 的共有点。

第二章第六讲相贯线

第二章第六讲相贯线

相贯线
二、相贯线的特殊情况
1.当两回转体具有公共轴线时，相贯线为一圆， 该圆的正面投影积聚为直线，水平投影反映圆的实 形。
相贯线
2.轴线平行的两圆柱的相贯线是两条平行的素 线。
图4-18 c 相贯线的特殊情况
相贯线
3.
图4-18 a 相贯线的特殊情况
相贯线
三、拱形柱与圆柱相贯
图4-19a 拱形柱与圆柱相交
相贯线
相贯体：两回转体相交。 相贯线：两回转立体表面相交产生的交线。 性质： 是两回转体表面的共有线，分界 线，一系列共有点的集合。 一般是封闭的空间曲线；特殊情 况下可能是平面曲线或直线。 形状取决于回转体的形状，大小 及两回转体之间的相对位置。
相贯线
求相贯线的实质：求基本体表面的 共有点，并将这些点光滑地连接起来。 求相贯线步骤：
1.求特殊点，能初步看出相贯线的投影 范围，拐弯情况。 2.求一般点。 3.判别可见性，并光滑连线。
相贯线
一、两圆柱垂直相交 例1：求作两圆柱相贯线的投影。
图4-15 两圆柱的相贯线
相贯线
近似画法：当两圆柱正交且直径相差较大时， 可用圆弧代替非圆曲线的相贯线，半径为大圆柱的 半径为大圆柱的 半径。 半径。
相贯线
图4-19b 拱形柱与圆柱相交
练习
练习Biblioteka 相贯线当直径不等的圆柱正交，在非积聚性投影的相 贯线的弯曲方向向着大圆柱的轴线 弯曲方向向着大圆柱的轴线。 弯曲方向向着大圆柱的轴线
图4-16c 两圆柱正交相贯线的变化
相贯线
例2：分析圆柱穿孔的相贯线的投影。
(b) 外圆柱面与内圆柱面相交 图4-17 两圆柱相交的三种形式
相贯线
(c)两圆柱内表面相交 (c)两圆柱内表面相交 图4-17 两圆柱相交的三种形式

相贯线

相贯线

2 半剖视图
适用范围：要求物体具有对称面；或接近对称且不对称部分 另有视图表示时；
视图与剖视之间应以 点划线分界； 半剖中已表达清楚的 结构，在半个视图的虚 线可不画；
3.局部剖视图
适用范围：仅有部分内部结构需要表达；或不宜画成全剖视 图或半剖视图的情况；
注意：剖视与视图的分界线为波浪线； 剖切范围不要过于零乱
相贯的画法
相贯---两立体（回转体）表面相交，其交线称为相贯线。
1、相贯线的性质：共有性、封闭性
相贯线是相交两立体表面的共有线，也是两立体表面的分界线。 由于立体均具有一定的范围，所以相贯线一般由封闭的空间线段组成。
相贯线的形状取决于立体的几何性质、相对大小以 及它们的相对位置。
x a y b r 2 2 2 y c z d r2
2
消去y得相贯线V面的投影的曲线方程
3）有公共内切球--柱锥相贯
4）两柱轴线平行
5）两锥共顶
影响相贯线形状的因素
影响相贯线的空间形状有 三个因素：相贯两曲面立 体的表面性质、相对位置、 尺寸大小。
正交两圆柱当直径相对变化时对相贯线形状的影响
两圆柱尺 寸关系
相贯线 的特点
水平圆柱直径大
两圆柱直径相等
A-A
A A A A A
3.旋转剖切 用两个相交的剖切面剖切
注意: 1)必须标注 2)两剖切面的交线应通过物体的回转轴线 3)先剖切、转平后再投影 4)一般用于盘类零件
当剖切后产生不完整的要素时，应按不剖绘制；
4.用组合的平面剖切—复合剖
复合剖可采用展 开画法，这时需 注明：x - x展开
5.用圆柱面剖切
求出特殊点1’和2’ 求出特殊点3’（4’） 过点1’、3’和2’作垂 直平分线，交点为 圆心O 以O为圆心画圆弧， 取代相贯线的投影。

2-4 两回转体表面相交 机械制图课件

2-4 两回转体表面相交 机械制图课件
(2)利用辅助平面法 求相贯虚实依次将各点 的投影连接为光滑 曲线并擦去被相贯 掉的轮廓线，加深 其余图线。
四、小结： 求相贯线的一般步骤
(1) 根据二相贯立体的形状及位置分析相贯线的形状； (2) 求相贯线上特殊位置各点及一般位置点的投影； (3) 判别可见性后依次连接各点，擦去被相贯掉的轮
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示仰视图形
请点击鼠标左键显示后视图形
第四节 两回转体表面相交
一、利用积聚性求相贯线 二、辅助平面法求相贯线 三、正交二圆柱相贯线分析 四、小结
一、利用积聚性求相贯线
相贯线的定义：二个回转体相互贯穿时， 表面的交线称为相贯线。
1. 相贯线的特性
相贯线是二立体表面上共有点的连线；
相贯线一般为一条封闭的空间曲线。
请点击鼠标左键显示后面内容
廓线，加深其余图线。
请点击鼠标左键显示后面内容
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示另一图形
请点击鼠标左键显示对比图形
请点击鼠标左键显示主视图形
一、利用积聚性求相贯线
2.相贯线的求法
利用圆柱的有积聚性的圆投影求相 贯线上各点的投影。
圆柱与圆柱（孔）的相贯线；
圆柱与圆锥的相贯线； 用积聚性法可求:

机械制图第三章 基本体投影

机械制图第三章 基本体投影

2'
5' 3' 4' 6'
4
PW
1" 2" 5"
4"
6" 3"
y
解题步骤
1、分析两圆柱的相对位置
2、判断相贯线的已知投影 是，由已知求未知投影.
3、求出相贯线上的特殊点.
4、求出一对一般点. 5、顺次光滑地连接各 点，并且判别可见性.
6、加粗可见轮廓线。
y
1
2
PH
5 36
一、辅助平面求点法——柱与孔
5 67 4
32
8
1 10 9
P Q
〔例8 〕 完成组合立体被截切后的投影
1' 4' (5')2' (3')
3" 5"
4" 2" 1"
3 5 1 4 2
2. 求曲面立体截交线的步骤
求曲面立体截交线的步骤：
找若
确定 截切 前基 本体 形状
判断 截平 面数 量及 位置
判断 各截 平面 形状
截平 面为 曲线 图形
1. 球的投影及表面取点
球的投影及表面取点： 辅助平面法。
1'
2'
如何求？
1" 3"
(2")
投投影影 可可见见否否？？
1 (2)
2. 作曲面立体投影及表面取点的注意问题
作曲面立体投影及表面取点的注意问题： （1）需要确定各投影面转向轮廓线的位置； （2）分清各条转向轮廓线在三个投影面的投影； （3）选择合适的辅助平面求点的投影。
4''

工程制图5第三章基本立体表面交线-相贯线

工程制图5第三章基本立体表面交线-相贯线

•
加强自身建设，增强个人的休养。202 0年11 月4日下 午12时 0分20. 11.420. 11.4
•
精益求精，追求卓越，因为相信而伟 大。202 0年11 月4日星 期三下 午12时 0分13 秒12:00:1320.1 1.4
•
专业精神和专业素养，进一步提升离 退休工 作的质 量和水 平。202 0年11 月下午1 2时0分 20.11.4 12:00N ovember 4, 2020
2.作图方法
求交线的实质是求各侧平面与回转面的交线。 • 分析各棱面与回转体表面的相对位置，从而确
定交线的形状。 • 求出各棱面与回转体表面的交线。 • 连接各段交线，并判断可见性。
11
例1：补全主视图
投空影间分分析析：：
由四于棱相柱贯的线四是个两侧立面体分表别与 面圆的柱共面有相线交，，所前以后相两贯侧线面的与圆 侧柱面轴投线影平积行聚，在截一交段线圆为弧两上段，直 水线平；投左影右积两聚侧在面矩与形圆上柱。轴线垂 直，截交线为两段圆弧。
封闭性—相贯线一般是封闭的空间折线（通常 由直线和曲线组成）或空间曲线。
7
8
求相贯线步骤
⒈ 交线分析
⑴ 空间分析： 分析相交两立体的表面形状， 形体大小及
相对位置，预见交线的形状。
⑵ 投影分析： 是否有积聚性投影？找出相贯线的已知投影，
预见未知投影，从而选择解题方法。
9
⒉ 作图
当相贯线的投影为非圆曲线时，其作图步骤为：
a'
b'
•• 1'
c'
• (d')
•• 2'
d" • a" (•b")1• "•(2c"")

两回转体表面的交线—相贯线(1)

两回转体表面的交线—相贯线(1)
选择辅助平面的原则： 为方便作图应使辅助平面与两回转体的交线形状为最简 单的直线或圆。
辅助平面的选择原则：
辅助平面的位置应取在两回转体相 贯的范围内。
辅助平面与两回转体表面的截交线 的投影要简单易画，例如直线或圆。对 圆柱，辅助平面应平行于圆柱的轴线， 但当圆柱的轴线垂直于某一投影面时， 也可垂直于轴线；圆锥时，应通过锥顶， 当圆锥的轴线垂直某一投影面时，也可 垂直轴线；圆球，应平行于投影面。
2’,(4’)
3’
4 (c) d
1
(3) (a)
b
2
1"
d" b"
QW
4"
2"
PW
c"
a"
RW
3"
注：圆柱与球相贯
当圆球与圆柱同轴且轴线平行于V面， 则相贯线圆在V面上的投影积聚为直线。
如是圆球开孔，相贯线同前面分析相同。 圆球与圆锥相交，其相贯线同前 面分析的情况相同。
例、求圆柱与半球相贯线主俯视图
作图方法：
★ 取特殊位置点； ★ 作一般位置点； ★ 判断点的可见性并连接
。
例：求两圆柱正交的相贯线。 （1）求特殊点：
a'
b'
• 1'
• c'
(•d')2•'•
d"• a"•(b1"•"•(2c"")
（2）求一般点： (3) 光滑连相贯线
d •
a •
•b
1• c• •2
辅助平面
P
2 1
两回转体表9;
6'
4' （5'） 2' （3'）

工程制图(第9讲)相贯线

工程制图(第9讲)相贯线

4.整理相贯立体在各投 影中的投影轮廓线
相贯线投影的近似画法
当两正交圆柱直径相差较大时，其相贯线的投影 可用圆弧近似代替。 d/2
1′ 2′ 4〞 3′(4′) 1〞(2〞) 3〞
d/2
1′′ 2′
d
4 1 2 1 2
3
三点画圆弧
以大圆柱半径为半径画弧
d
两圆柱正交相贯的基本形式及其投影特点
当圆柱直径变化时，相贯线的变化趋势。
⒉ 作图
当相贯线的投影为非圆曲线时，其作图步骤为： ⑴ 找点 ☆ 先找特殊点
特殊点包括：最上点、最下点、最左点、 最右点、最前点、最后点、轮廓线上的点等。
☆ 补充若干中间点 ⑵连线 ⑶检查、加深
尤其注意检查回转体轮廓素线的投影。
三、两圆柱体相贯 ⒈ 相贯线的产生：
外表面与外表面相交， 外表面与内表面相交， 内表面与内表面相交。 ⒉ 求相贯线的方法：
求相贯线投影的方法
求相贯线的实质-----求立体表面的共有点
常用的求相贯线上点的投影的方法有：
①表面取点法：利用积聚性 ②辅助平面法：a）作辅助平面 b）和立体产生两条截交线 c）截交线的交点即为共有点
一、表面取点法
两相贯立体中如果有一正圆 柱轴线垂直于某一投影面，就可 以利用圆柱面投影的积聚性得到 相贯线的一个投影。然后，用表 面取点的方法求出相贯线的其他 投影。
PV
P1V 3"
5"
6" 4" 2"
3 5 2 1 6 4
PV
2'
QV 5',6' 1' 3',4' 4" 5"
2"

两共轴回转体表面相贯线的形状为

两共轴回转体表面相贯线的形状为

两共轴回转体表面相贯线的形状1. 引言两共轴回转体是一种几何形体，它由两个共轴旋转而成。

在制造和设计领域中，了解两共轴回转体表面相贯线的形状对于完成复杂的加工任务非常重要。

本文将详细介绍两共轴回转体表面相贯线的形状及其相关概念。

2. 什么是两共轴回转体？两共轴回转体是由两个平行且共享同一旋转轴的曲面组成。

这种几何形体常常出现在机械工程、航空航天以及汽车工业中。

3. 相贯线的定义在几何学中，相贯线指的是由两个曲面交汇而产生的曲线。

对于两个共轴回转体来说，它们的表面相贯线就是它们相交所形成的曲线。

4. 两共轴回转体表面相贯线的性质4.1 曲率半径变化根据曲率半径变化的情况，我们可以将两共轴回转体表面相贯线分为以下几类：•当曲率半径变化连续而且对称时，相贯线为圆弧。

•当曲率半径变化不连续或者不对称时，相贯线为非圆弧。

4.2 相贯线的形状两共轴回转体表面相贯线的形状取决于两个回转体的轮廓曲线。

以下是几种常见的相贯线形状：•椭圆形：当两个回转体的轮廓曲线为椭圆时，相贯线呈现出椭圆形状。

•双曲线形：当一个回转体的轮廓曲线为双曲线，另一个回转体的轮廓曲线为椭圆时，相贯线呈现出双曲线形状。

•直角螺旋形：当一个回转体的轮廓曲线为直角螺旋，另一个回转体的轮廓曲线为椭圆时，相贯线呈现出直角螺旋形状。

5. 相贯线的计算方法计算两共轴回转体表面相贯线的形状需要使用数学方法和计算机模拟。

以下是常用的计算方法：5.1 参数方程法参数方程法是一种常用于描述曲线的方法，它通过引入参数来表示曲线上的点。

对于两共轴回转体表面相贯线的计算，可以使用参数方程法来描述曲线的形状。

5.2 数值模拟法数值模拟法是使用计算机进行模拟和计算的方法。

通过将两共轴回转体的轮廓曲线输入计算机程序，可以得到相贯线的形状。

6. 应用领域了解两共轴回转体表面相贯线的形状对于以下领域非常重要：•制造工艺：在机械制造过程中，了解相贯线的形状可以帮助工程师选择合适的加工工艺和设备。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

两回转体表面相交
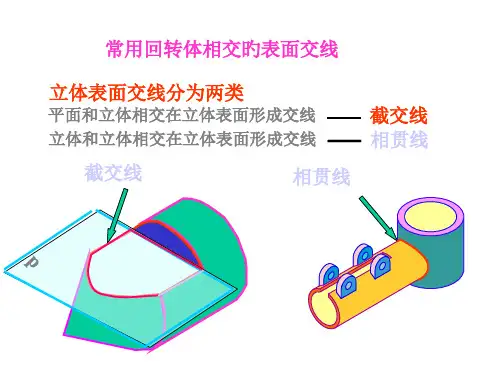
（一）、相贯线的概述1.
相贯线的概念
两立体表面的交线称为相贯线。

相贯线不仅出现在两立体外表面，有时还见到两立体内表面，以及立体被穿孔的情况。

2.影响相贯线形状的因素
相交的两立体的形状。

相交的两立体的相对尺寸大小。

相交的两立体的相对位置。

3.相贯线的特性
① 一般为空间曲线，特殊情况下为平面曲线。

② 为两回转体表面的共有线。

③ 为两回转体表面的分界线。

4.
求相贯线的方法：
① 表面取点法
② 辅助平面法
5.求相贯线的步骤:
① 求特殊位置的点：转向线上的点、最高点、最低点、最左点、最右点、最前点、最后点。

② 求一般位置点。

③ 判断可见性：只有当相贯线同时属于两立体表面的可见部分时,才可见。

（二）、表面取点法1.
什么是表面取点法
当相交的两回转体中有一个是圆柱且轴线垂直于投影面时，圆柱面在该投影
面上的投影积聚为圆，因此，相贯线在该投影面上的投影就积聚在圆柱面有积聚性
的投影(圆)上。

这时，可以将相贯线看成是另一回转面上的曲线，利用回转面上
取点的方法作出相贯线的其它投影。

表面取点法只适用于相交两回转体中至少有一个是圆柱，并且其轴线与投影
面垂直的情况下。

2.作图举例
已知两圆柱轴线垂直相交，求它们的相贯线投影。

分析：由图可以看出，大圆柱的轴线垂直于侧面，小圆柱的轴线垂直于水平面，两圆柱轴线垂直相交。

因为相贯线是两圆柱体表面上的共有线，所以相贯线的侧面投影与大圆柱的侧面投影重合，水平投影与小圆柱的水平投影重合。

需要求相贯线的正面投影。

因相贯线前后对称，相贯线前、后两部分的正面投影重合。

作图：
1）作特殊点最左、最右、最前、最后、最高、最低点，转向轮廓线上点。

2）作一般点
3）判别可见性并连线作图结果如图 d 所示。

（a）已知条件（b）作特殊点投影
（c）作一般点投影（d）作图结果求
正交圆柱体相贯线
（三）辅助平面法
1.什么是辅助平面法
假想的用一个平面截切相贯的两回转体，分别求出该平面与两回转体的截交线，则两组截交线的交点，即为相贯线上的点。

这种求作相贯线的方法，称为辅助平面法。

选择辅助平面的位置和数量应根据两回转体的具体情况而定。

辅助平面的设定原则是：要使所设立的辅助平面与两个回转体表面截交线的投影简单易画，如直线、圆等。

通常情况下辅助平面应取为与某投影面平行或垂直的平面作为辅助平面。

(a)立体图 (b)垂直于轴线的辅助平面 (c)过顶点的辅助平面
选择辅助平面
2.作图举例
例如图 a 所示，作圆柱与圆锥的相贯线。

（a）已知条件（b）作特殊点投影
（c）作一般点投影（d）作图结果求
圆柱体和圆锥体相贯线
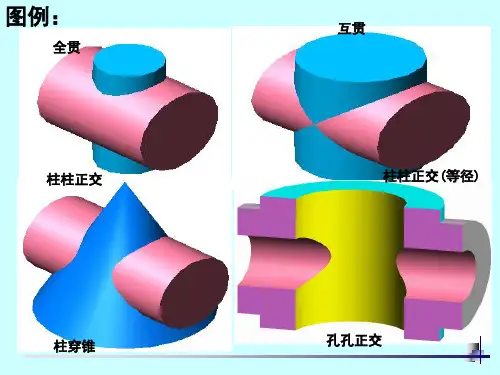
（三）、回转体相贯线的讨论
如前所述，两回转体相交产生的相贯线的形状由两个回转体的形状、大小和它们的相对位置确定，可能是封闭的空间曲线，也可以是封闭的平面曲线、直线或者曲线与直线的组合。

1）穿孔型相贯线
机件上除了两回转体实体相交产生相贯的情况，还存在一个实体被另一个实体贯穿（或挖切、穿孔）的情况。

（a）圆柱穿孔（b）四通圆筒穿
孔型相贯线
2）两回转体半径尺寸和轴线相对位置变化的影响
图a 所示为两个不同半径的圆柱相贯所产生的相贯线情形；图 b 所示为两个相互垂直的圆柱的轴线位置的变动所产生的相贯线情形。

(a)尺寸变化的情形
(b)两轴线位置变动的情形
3）相贯线的特殊情形
① 同轴的回转体，相贯线是垂直于轴线的平面圆，在与轴线垂直的投影面上的投影是圆，在与轴线平行的投影面上的投影为直线。

② 当轴线相交的两回转体内切于一个球面时相贯线是两个相交的椭圆平面曲线，若椭圆平面垂直于投影面，则相贯线在该投影面上的投影为交叉的直线。

③ 当两个圆柱轴线平行及两个圆锥共顶点时，相贯线为直线。

4）相贯线的简化画法
两正交圆柱在工程中比较常见，其相贯线是两圆柱体相交中自然形成的。

按照制图国家标准，在不影响看图的情况下这种相贯线可以采用简化形式表达，即用圆弧替代，称作三点圆弧法。

相贯线的简化画法
用大圆柱的半径R=0.5D 为半径；分别以大、小圆柱的外轮廓交点为圆心作圆弧得交点3；以该点3 为圆心、R 为半径作弧连接即可。

5）相贯线的模糊画法
国家标准《技术制图》GB/T 16675.1-1996 中对一些形体的相贯线制订新的简化画法，如“模糊画法”。

下图所示为圆柱与圆台的正交相贯线的模糊画法。

这些规定读者可参阅相关国标。

(a) 简化前 (b) 简化后相
贯线的模糊画法。