当前位置：文档之家 › 第二章插值法-上海海事大学概论

第二章插值法-上海海事大学概论

  • 格式：ppt
  • 大小：2.38 MB
  • 文档页数：93

下载文档原格式

  / 93

合集下载

上海交大数值分析数值分析21插值法精品PPT课件

上海交大数值分析数值分析21插值法精品PPT课件

是插值原则.
思考题 当数据点(xi, yi)给定后，满 足插值条件的插值函数φ(x)有多少
种类型？
答 有许多种。例如给出平面上两 个点，则过这两个点的曲线有无穷 多种，可以是代数多项式、三角多 项式、有理函数等等，但最简单而 最常用的是代数多项式，它有许多 良好的性质，故本章仅考虑代数多 项式插值问题
The wife said: "No, they're TEN!" "But I have counted them: 0, 1, 2, ..."
A mathematician, a physicist, and an engineer were traveling through Scotland when they saw a black sheep through the window of the train.
注：插值问题和曲线拟合问题统称 函数逼近问题！
三、插值问题的定义
1. 插值问题的有关概念 已知条件
设给出关于函数y= f (x)的一组函数值，
x x0 x1 y y0 y1
x2 … xn y2 … yn
其中x0 , x1, x2, …, xn是区间[a,b]上的互异点(因为 )， 函数是这样的映射：一个x唯一的对应一个y
2. 代数多项式插值问题 已知条件 设给出关于函数y= f (x)的一组函数值，
x x0 x1 x2 … xn y y0 y1 y2 … yn
其中x0 , x1, x2, …, xn是区间[a, b]上 的互异点(因为函数是这样的映射：一个x唯 一的对应一个y)(一共n+1个节点),
求 一个次数不超过n的多项式
P n ( x ) a 0 a 1 x a 2 x 2 a n x n

第二章 插值法

第二章 插值法

(2.1)
则称 ϕ (x ) 为f(x)的一个插值函数 f(x)为被插函数, 点 ( )的一个插值函数, ( ) 被插函数 插值函数 xi为插值节点 称(2.1)式为插值条件 而误差函数 插值节点, 2.1)式为插值条件, 式为插值条件 R(x)= f ( x ) − ϕ ( x) 称为插值余项, 区间[a, b]称为插值 称为插值余项 区间[ 插值余项 ]称为插值 区间, 插值点在插值区间内的称为内插 否则称外插 内插, 区间 插值点在插值区间内的称为内插 否则称外插
这是一个关于待定参数 a 0 , a 1 , L , a n 的n+1阶线性方 阶线性方 惟一性说明，不论用何种方法来构造， 惟一性说明，不论用何种方法来构造，也不论用何种 程组, 形式来表示插值多项式, 程组,其系数矩阵行列式为 只要满足插值条件(2.1)其结 形式来表示插值多项式,只要满足插值条件(2.1)其结 果都是相互恒等的。 果都是相互恒等的。
y1 − y 0 p ( x) = y 0 + ( x − x0 ) x1 − x0
x − x0 x − x1 p ( x) = y0 + y1 x0 − x1 x1 − x0
为了便于推广， 为了便于推广，记 这是一次函 数,且有性质
x − x0 x − x1 l 0 ( x) = , l1 ( x) = x0 − x1 x1 − x0
2 0 2 1 2 2
的行列式是范德蒙行列式， 的行列式是范德蒙行列式，当 方程组的解唯一。 方程组的解唯一。
x0 ≠ x1 ≠ x 2
时，
为了与下一节的Lagrange插值公式比较,仿线性插值,用 插值公式比较,仿线性插值, 为了与下一节的 插值公式比较 基函数的方法求解方程组。 基函数的方法求解方程组。先考察一个特殊的二次插值 问题： 问题： 使其满足条件： 求二次式 l 0 ( x) ,使其满足条件：

1.2第二章_内插法

1.2第二章_内插法

二. 比例双内插（二元函数）
当函数有两个自变量时，用比例双内插求 近似解。
例2－1－2：由例2－1－1的计算结果，求h ＝13.4m，α＝4.4时的D？
10 13.4
20
3
6.2
12.3
4
4.6 6.2
9.3
4.4
5.7
5
3.7 5.0
7.4
D＝6.2＋ 5.0 - 6.2 （4.4－4）＝5.7n mile 5-4
mile
10
（2）求α＝5′，h＝13.4m时的D2？
α h 10 13.4
20
3 6.2
12.3
4 4.6
3
5 3.7 5.0
7.4
D1＝D0＋
Dh1--Dh（0 h－h0）＝3.7＋
7.4 20
-
130.（7 13.4－10）＝5.0n
mile
10
2. 比例反内插 内插的逆运算，y＝f（x），已知y求x？
5
3.7
7.4
z
=z00+
z 10 x1
- z 00 - x0
(x
-
x0)+
z 01 y1
-
z 00 y0
(y
-
y0 )
Z ＝4.6＋
9.3－4.6 20 - 10
(13.4－10）＋
3.7－4.6 5-4
（4.4－4）＝5.8
n
mile
第二节 变率内插
当函数是非线性函数时，如果用比例内 插计算将会导致一定的计算误差， 为了尽量减小该误差，则引进了变率内 插。
内插法：
利用函数表册，根据任意居间引数查取 相应函数的方法。

线性插值法 - 插值法

线性插值法 - 插值法

线性插值法- 插值法许多实际问题都用函数y=f（x）来表示某种内在规律的数量关系，其中相当一部分函数是通过实验或观测得到的。

虽然f（x）在[a,b]上是存在的，有的还是连续的，但只能给出[a,b]上的一系列点xi的函数值yi=f(xi)(i=0,1,……,n)，这只是一张函数表，有的函数虽然有解析表达式，但由于计算复杂，使用不方便，通常也造一个函数表，如大家熟悉的三角函数表、对数表等。

为了研究函数的变化规律，往往需要求出不在表上的函数值。

因此，我们希望可以根据给定的函数表做一个既能反映函数f(x)的特性，又便于计算的简单函数P(x)。

用P(x)近似f(X)。

通常选一类简单的函数作为P(x)，并使P(xi)=f(xi)对i =1,2,……,n成立。

这样确定下来的P(x)就是我们希望的插值函数，此即为插值法。

线性插值法- 什么是线性插值法线性插值是数学、计算机图形学等领域广泛使用的一种简单插值方法。

线性插值法- 如何进行线性插值假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的y值。

根据图中所示，我们得到（y-y0）(x1-x0)=(y1-y0)(x-x0)假设方程两边的值为α，那么这个值就是插值系数—从x0到x的距离与从x0到x1距离的比值。

由于x值已知，所以可以从公式得到α的值α=(x-x0)/(x1-x0)同样，α=(y-y0)/(y1-y0)这样，在代数上就可以表示成为：y = (1- α)y0 + αy1或者，y = y0 + α(y1 - y0)这样通过α就可以直接得到y。

实际上，即使x不在x0到x1之间并且α也不是介于0到1之间，这个公式也是成立的。

在这种情况下，这种方法叫作线性外插—参见外插值。

已知y求x的过程与以上过程相同，只是x与y要进行交换。

第2章插值法

第2章插值法
的n次插值多项式，则对于任何 xa，,b有
Rn (x)
f (n1) ( )
(n 1)!
n1
(
x)
（2.9）
x
其中 n1(x) n (x xi ) , (a,且b)依赖于 。
证明 点都是
由插i值0 条件
知
的零点，故可设Pn(xi)f(xi)
Rn (xi ) 0(i 0,，1,即插, n值) 节
当复杂，使用起来很不方便。面对这些情况，总希望 根据所得函数表（或结构复杂的解析表达式），构造
某个简单函数P(x)作为 的近似。
插值法是解决此类问题的一种比较古老的、
然而却是目前常用f 的x方法，它不仅直接广泛地
应用于生产实际和科学研究中，而且也是进一 步学习数值计算方法的基础。
4
现在你正浏览到当前第四页，共一百零三页。
（图2-3
例1 已知
分别用线性插值和抛物插值
求
的1值0 。1 0,012 11,1 14 1 42
115
15
现在你正浏览到当前第十五页，共一百零三页。
解 因为115在100和121之间，故取节点x0=100，x1=121相应地有 y0=10，y1=11，于是，由线性插值公式（2.5）可得
L1
(
x)
17
现在你正浏览到当前第十七页，共一百零三页。
输入xi,yi,n,x
j=0,1,```,n
P=1
y=0
k=0,1,```,n
k=j?
否 P=P*(x-xj)(xk-xj)
是
输出x,y
图2-4
y=y+P*yk
18
现在你正浏览到当前第十八页，共一百零三页。
lk (x)

第2章 插值法

第2章 插值法

2.3.2 均差及其性质
差商的基本性质:
由(3.4)得差商表:
k xk f(xk) 一阶差商 二阶差商 三阶差商 …
0 x0 f(x0) 1 x1 f(x1) 2 x2 f(x2) 3 x3 f(x3) 4 x4 f(x4) ┆ ┆┆
f[x0, x1] f[x1, x2] f[x2, x3] f[x3, x4]
。
1.0
这说明用高次插值多项
式Ln(x)近似f(x)效果并不
0.5
好，因而通常不用高次
插值，而用分段低次插值。
-5
0
5x
二、分段线性插值 所谓分段线性插值就是用通过插值点的折线段逼近f(x).
二、分段三次埃尔米特插值 分段线性插值函数导数间断，若已知节点上函数值和
导数，可构造一个导数连续的插值函数Ih(x)，满足
yk
0
xk
y=L1(x) y=f(x)
yk+1
xk+1
x
y
1 1 图 2-3
1
0
xk
xk+1
x
几何上就是通过三点（xk-1,yk-1),(xk,yk),(xk+1,yk+1)的抛物线。
y 1
0
Xk-1
x xk Xk+1
图 2-4
2.2.2 拉格朗日插值多项式
需要指出(2.3)式与（2.5）式是当n=1和n=2时的特殊 情形。
例1 已知sin0.32=0.314567, sin0.34=0.333487, sin0.36=
0.352274,用抛物插值计算sin0.3367的值, 并估计误差.
§2.3 差商与牛顿插值
2.3.1 插值多项式的逐次生成

第2章 插值法2

a0 = f0 f1 − f 0 a1 = x1 − x 0 ⇒ f2 − f0 f1 − f 0 − x2 − x0 x1 − x 0 a2 = x 2 − x1 LL
Pn ( x j ) = f j
Pn ( x) = a0 + a1 ( x − x0 ) + a2 ( x − x0 )( x − x1 )
x0 , x1 , K, xk 的k阶
4
差商（均差） 二. 差商（均差）的性质
• 性质1:k阶差商可以表示成k+1个函数值 f ( x0 ), f ( x1 ),L , f ( xk ) 的线性组合,即
f [ x0 , x1 ,L, xk ] = ∑
j =0 k
f (x j )
( x j − x0 )L( x j − x j −1 )( x j − x j +1 )L( x j − xn )
f1 − f 0 P ( x) = f 0 + ( x − x0 ) 1 x1 − x0 ( fi = f ( xi ) = yi )
出发，将它推广到具有n+1个插值点的情况， 出发，将它推广到具有n+1个插值点的情况，可 n+1个插值点的情况 把插值多项式表示为
Pn ( x) = a0 + a1 ( x − x0 ) + a2 ( x − x0 )( x − x1 ) + L + an ( x − x0 ) L) − f ( x0 ) 例:
f [ x0 , x1 ] =
x1 − x0
f0 f1 = + x0 − x1 x1 − x0
f [ x0 , x2 ] − f [ x0 , x1 ] f [ x0 , x1 , x2 ] = x2 − x1

数值分析(第5版)第2章-插值法 ppt课件



x4 94

1(x 5
4)
插值多项式为
1
1
L1( x)
y0l0 ( x) y1l1( x) 2
5
( x 9) 3 ( x 4) 5
2 ( x 9) 3 ( x 4) 1 ( x 6)
5
5
5
所以
7

L1 (7)

13 5

2.6
ppt课件
项式(2-2) 存在且唯一。证毕。
ppt课件
5
第二节 拉格朗日插值
一、基函数
考虑下面最简单`最基本的插值问题。求n 次多项 式 l i(x) (i=0,1, …, n)，使其满足条件
0 , j i li ( xj ) 1, j i ( j 0,1, , n)
故可设
li ( x) A( x x0 )( x xi1 )( x xi1 )( x xn )
15
例2 求过点(1,2), (1,0), (3,6), (4,3)的三次插值多项式。
解 以 x0 1, x1 1, x2 3, x3 4 为节点的基函数
分别为:
l0
(
x)

( x 1)( x 3)( x 4) (1 1)(1 3)(1 4)

Pn(x)=a0+a1x+a2x2+...+anxn (2-2)
则由插值条件式Pn(xi)=yi (i=0,1, ..., n) 可得关于系数 a0 ,a1 , …,an的线性代数方程组
ppt课件
3

a0 a0

a1 x0 a1 x1

《数值分析》课件-第2章


（1）
则称ϕ (x)
为
f
(x)
在
Φ
中关于节点
{xi
}n i=0
的一个插值函数。
f (x) ——被插值函数； [a, b] ——插值区间；
{xi
}n i=0
——插值节点；
式（1）——插值条件.
2004-9-9
3
2 . 几何意义、内插法、外插法
M~
=
max{x
i
}n i =0
m~
=
min{x
i
}n i =0
2004-9-9
内插
x ∈[m~, M~ ]
外插 x ∈[a, b] but x ∉[m~, M~ ]
4
3. 多项式插值问题
对于不同的函数族Φ的选择，得到不同的插值 问题
当Φ为一些三角函数的多项式集合时:三角插值; 当Φ为一些有理分式集合时：有理插值； 当Φ为一些多项式集合时：多项式插值
{ } 特别的取 Φ = Pn =∆ span 1, x, x2 ,L, xn , 即
g
(t )
在区间
[a,
b]
上的
n
+
2
个互异零点：
x
、
{xi
}n i=0
当 g(t) 充分光滑时， g (n+1) (t) 在开区间 (a, b) 内至少存在一个零点ξ
g g
(n (n
+1) +1)
(t) =
(ξ ) =
f( 0
n+1)
(t
)
−
(n
+
1)!k
(
x)
⇒
k
(

数值分析-课件-第02章插值法1概论


解
制差商表
xi 4.0002 4.0104 4.0233 4.0294
lg xi 0.6020817 0.6031877 0.6045824 0.6052404
一阶差商
二阶差商
0.108431 0.108116 0.107869
-0.0136 -0.0130
根据问题知插值点x=4.01在 x0 与 x1 之间，故可用前三点 x0 , x1, x2 的二次插值多项式计算，即用
4
1, 2
sin3
3 2
分别利用 sin x 的1次、2次 Lagrange 插值计算 sin 50， 并
估计误差。
解： n = 1 分别利用x0, x1 以及 x1, x2 计算
利用
x0 6 , x1 4
L1
(
x)
x /
/ 6
4 /4
1 2
x /
/ 4
6 /6
sin 500
L1
(
5
18
P1 x
y0
y1 x1
y0 x0
x
x0
x x1 x0 x1
y0
x x0 x1 x0
y1
1 i0
li
xyi
l0(x)
l1(x)
2020/11/17
2.6
Numerical Analysis
构造基函数
l
j
(x)
(x x0 )(x (x j x0 )(x j
x1 ) x1 )
一般地，xi 点的 n 阶向前差分
是 yi , yi1,
n yi n1 yi1 n1 yi
, yin 的线性组合。
向后差分
n yi n1 yi n1 yi1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y f (x)
x0
x1
x2
x
3
x3
x4
我们仅介绍多项式插值,即如果已知函数f (x)在n+1个互异
点的值yi=f (xi) (i=0,1,2,,n),求一个次数不高于n的多项式
Pn(x)=a0+a1x+a2x2++anxn ,
(1.2)
使
Pn(xi)=yi (i=0,1,2,,n)
为了确定Pn(x)的n+1个系数,由上述条件得线性方程组
1(x),2 (x),...n (x)组成的函数空间,所以 p(x) n
可表示为
ai ,
p(x) a00 (x) a11(x) ... ann (x)
这里
i 0,1,2,...n是(n+1)个待定常数
它可根据条件(1.1)确定.
当 k (x) xk k 0,1,2,...n
Hn Span 1, x, x2,...xn 表示次数不超过n次的多项式集合，
p(xi ) yi i 0,1,2,...n (1.1)
称 p(x) 为 y =f(x) 的插值函数，点 x1, x2 ,....xn
称为插值节点，包含插值节点的区间[a, b] 称为插值区间.
1
通常 p(x) n Span0,1,...n,其中 i (x) i 0,1,2,...n
是一组在 [a, b]上线性无关的函数族, n 表示由
2 j 1
x xj x0 x j
类似地有
l1( x)
(x ( x1
x0 )( x0 )(
x x2 ) x1 x2 )
2 j 0
x xj x1 x j
j 1
l2 ( x)
( x x0 )( x x1) ( x2 x0 )( x2 x1)
1 j0
x xj x2 x j
∵ l0 ( x1) l0 ( x2 ) 0
∴ 可令
l0 ( x) ( x x1)( x x2 )
又∵ l0 ( x0 ) 1 ∴ ( x0 x1)( x0 x2 ) 1
1
( x0 x1)( x0 x2 )
则
l0 ( x)
(x ( x0
x1)( x x2 ) x1)( x0 x2 )
L2(x) l0(x) y0 l1(x) y1 l2(x) y2 (2.5)
其中 li (x) (i 0,1,2) 均为二次多项式 , 且满足
li
(xj
)
ij
0 1
ji ji
(i, j 0,1,2)
10
用待定系数法可确定 li (x) (i 0,1,2) 。
例如为确定二次多项式 l0 ( x) ,
aa00 aa11xx01 aa22xx1022 aannxx10nnyy10 a0 a1 xn a2 xn2 an xnn yn
其系数矩阵是n+1阶范德蒙(Vandermonde)行列式
4
1 x0
1 x1 V ( x0 , x1,, xn ) 1 x2
x02 x0n x12 x1n x22 x2n
1 xn xn2 xnn
∵ xi≠xj ,(i≠j),∴此范德蒙行列式的值不为零,方程组有唯一 解a0,a1,a2,,an.
由此可知:满足插值条件(1.1)的插值多项式(1.2)式 是唯一存在的.
虽然此法可以求出唯一的插值多项式,但是计算量太大,
并不实用。下面介绍拉格朗日和牛顿两种插值法。
5
返回
6 §2 拉格朗日插值法。
所以 p(x) Hn 有
p(x) a0 a1x a2x2 ... an xn
2
(1.2)
(1.2)称为插值多项式，如果为三角函数，则为三角插值， 同理还有分段多项式插值，有理插值等等.
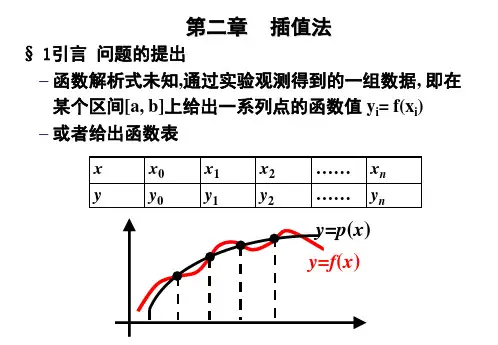
从几何上看，插值问题就是求过n+1个点
( xi, yi ) 的曲线，使它近似于已给函数
p(x) f(x)
质如下：
l0 ( x0 ) 1
l1
(
x0
)
0
, l0 ( x1) 0 , l1( x1) 1
可写成
li
(x
j
)
ijΒιβλιοθήκη 0 1ji ji(i, j 0,1)
拉格朗日线性插值基函数 li (x) (i 0,1) 均为x的一 次多项式,而拉格朗日线性插值多项式L1(x)插值基函数的
线性组合,相当于用直线逼近曲线。(P24)
0.7071
∴
sin
40o
P1(40o )
P1
2
9
P1(0.6981)
0.6981 0.7854 0.5 0.6981 0.5236 0.7071
0.5236 0.7854
0.7854 0.5236
0.6380
(sin 40o 的准确值是0.6428)
9 二次插值
已知三点 (xi,yi) (i=0,1,2), 求一个二次多项式 P2(x) , 使 P2 ( xi ) = yi ( i = 0,1,2) 由线性插值的启示和拉格朗日线性插值公式的特点,可令
8 例 已知 sin 30o 0.5,sin 45o 0.7071 ,求 sin 40o
解
∵
x0
30o
6
0.5236(弧度),
y0
0.5
x1
45o
4
0.7854(弧度),
y1
0.7071
∴
L1 ( x)
x 0.7854 0.5236 0.7854
0.5
x 0.5236 0.7854 0.5236
第二章 插值法
§1 前言 实际问题中若给定函数 y =f(x) 是区间[a, b]
上的一个列表函数 ( xi, yi ) i 0,1,2,...n
如果 a x0 x1 ....... xn b ,且 y =f(x) 在区间
上是连续的，要求用一个简单的便于计算的解析表达式 p(x) 在区间 上近似 y =f(x) ，使
线性插值 已知两点 (x0,y0) , (x1,y1) , 求一次多项式 P1(x) , 使 P1(x0)=y0 ,P1(x1)=y1 ,即求一条过 (x0,y0) 和 (x1,y1)的直线 y=P1(x) .
由直线的两点式方程
y y0 x x0 y1 y0 x1 x0
得
y
x x1 x0 x1
y0
x x0 x1 x0
y1
(2.1)称为拉格朗日线性插值公式。
(2.1)
7
如记
l0 ( x)
x x1 x0 x1
l1( x)
x x0 x1 x0
则(2.1)可写成
L1(x) l0 (x) y0 l1(x) y1
(2.3)
其中 li (x) (i 0,1) 称为拉格朗日线性插值基函数,其性