当前位置：文档之家 › 第二章插值法讲解

第二章插值法讲解

  • 格式：ppt
  • 大小：1.59 MB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

第二章 插值法--课堂

第二章 插值法--课堂

考察函数
右图给出了 和 的图像,当n 增大时, 在两端 会发出激烈的振荡 ,这就是所谓龙格现 象。该现象表明,在 大范围内使用高次 插值,逼近的效果往 往是不理想的
另外，从舍入误差来看，高次插值误差的传播 也较为严重，在一个节点上产生的舍入误差会在计 算中不断扩大，并传播到其它节点上。因此，次数 太高的高次插值多项式并不实用，因为节点数增加 时，计算量增大了，但插值函数的精度并未提高。 为克服在区间上进行高次插值所造成的龙格现象， 采用分段插值的方法，将插值区间分成若干个小的 区间，在每个小区间进行线性插值，然后相互连接 ，用连接相邻节点的折线逼近被插函数，这种把插 值区间分段的方法就是分段线性插值法。
有2n+2个根，但 是不高于2n+1次的多项式
，所以
，即
惟一性得证。
定理5.4 若f(x)在a,b上存在2n+2阶导数，则 2n+1次Hermite插值多项式的余项为
其中 定理的证明可仿照Lagrange插值余项的证 明方法请同学们自行证明
实际中使用最广泛的是三次Hermite插值多项式, 即 n=1的情况
表示互为逆运算。
至于如何实现这些基本运算之
间的联系和转化，途径是多种 多样的，结果是丰富多彩的，魅力是无群无尽的
§4 埃尔米特插值
注： N 个条件可以确定 N 1 阶多项式。 要求在1个节点 x0 处直到m0 阶导数都相等的插值
多项式即为Taylor多项式 其余项为
一般只考虑 f 与f ’的值。
二、分段三次埃尔米特插值
分段线性插值函数导数间断，若已知节点上函数值和
导数，可构造一个导数连续的插值函数Ih(x)，满足
§6 三次样条插值
一、样条插值的概念

数值方法第二章 插值法2

数值方法第二章 插值法2
3
1 f ( ) ( x) 2
3
1 2 R1 ( x) ( x x0 )(x x1 ) 8 3 1 2 R1 (115) (115 100)(115 121 ) 8 3 1 (115 100)(115 121 max 2 ) 100 ,121 8
当选择代数多项式作为插值函数类时，称为代数多项 式插值问题:
代数多项式插值问题:
设函数y=f(x)在[a,b]有定义, 且已知在n+1个点 a≤x0<x1<……<xn≤b上的函数值y0, y1,……,yn.,要求一 个次数不高于n的多项式
Pn ( x) a0 a1 x a2 x 2 an x n
这是一个线性函数，在几何上就是通过曲线y=f(x)上 的两点(x0,y0)和(x1,y1)作一直线y=L1(x)近似代替曲线 y=f(x),故两点插值又名线性插值
线性插值的几何意义

n=2时
( x x1 )( x x2 ) l0 ( x ) ( x0 x1 )( x0 x2 )
其中，k(x)为待定函数
作辅助函数 F (t ) f (t ) P (t ) k ( x) (t ) n n 1 不难看出F(t)具有以下特点:
(1) F(x)=F(xi)=0(i=0,1….n)也就是F(t)有n+2个零点即x, x0,x1,…,xn. (2)在[a,b]上具有n+1阶导数，且
第2章 插值法
§1
引言 § 2 拉格朗日插值多项式 § 3 牛顿插值多项式
§4 §5 §6
分段低次插值 三次样条插值 数值微分
}
§1
引言
1.1 插值问题及代数多项式插值

数值分析第二章 插值法

数值分析第二章 插值法

(j,k=0,1,…,n)
( x x0 )( x xk 1 )( x xk 1 )( x xn ) lk ( x ) ( xk x0 )( xk xk 1 )( xk xk 1 )( xk xn )
n1 ( x ) ( x xk ) n1 ' ( xk )
n
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
• 性质 （2）k阶均差可重新写为：
f [ x1 , x2 ,, xk ] f [ x0 , x1 , xk 1 ] f [ x0 , x1 , xk ] xk x0
• 均差的计算
三、均差与牛顿插值
1.均差与性质
• 均差定义
类似地称 2 f k f k 1 f k 为 xk 处的二阶差分. 一般地称 n f k n1 f k 1 n1 f k 为 xk 处的n阶差分.
• 均差与差分关系
• 牛顿前插公式
n f k (1) f nk j , j 0 j
求5、6月份的日照时间的变化规律。 • 多项式插值的存在唯一性
一、引言
2.多项式插值
• 一个例子 日照时间的变化设为 y(x)=a0+ a1x + a2x2, 根据三组数据: (1, 13.53), (31, 14.21),(61, 14.40)， 导出关于a0，a1，a2的线性方程组
a0 a1 a2 13.53 2 a0 31a1 (31) a2 14.21 2 a0 61a1 (61) a2 14.40
三、均差与牛顿插值
3.差分形式的牛顿插值公式
若x0,x1,…,xn 为等距节点，即xk=x0+kh (k=0,1,...,n) 时，可将牛顿插值公式简化

第二章插值法

第二章插值法

lk ( xk 1 ) 0
n=2的情况，假定插值节点为
xk 1 , xk , xk 1 , 要求一个二次插值多项式L2 ( x)，使它满足 L2 ( x j ) y j ( j k 1, k , k 1)
y L2 ( x)在几何上就是通过三点(xk-1 , yk 1 ),(xk , yk ),(xk+1, yk 1 )的抛物线
插值法
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 引言 拉格朗日插值 均差与牛顿插值公式 差分与等距节点插值 埃尔米特插值 分段低次插值 三次样条插值
一、插值问题
或者函数本身只是 一组实验数据，很 难对函数的性质进 行分析
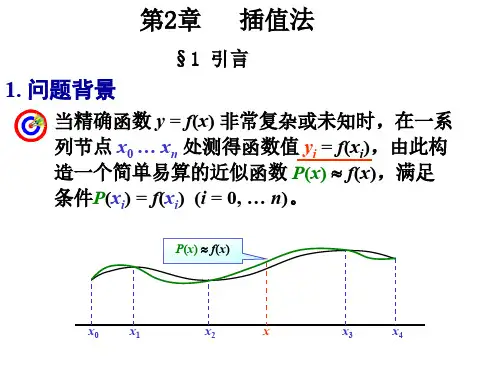
对函数f (x),其函数形式可能很复杂且不利于在计算机上 ,
设函数
y f ( x ) 在区间 [a, b] 上有定义，且已知在
a x0 x1 x2 xn b
f ( xi ) yi , i 0,1,, n
如果存在一个简单函数 P ( x )，使得
P( xi ) f ( xi ) yi , i 0,1,, n
xx x x
如函数y sin x, 若给定 0, ]上5个等分点 [
其插值函数的图象如图
对于被插函数 ( x)和插值函数 ( x) f P
在节点xi处的函数值必然相等
但在节点外 ( x)的值可能就会偏离 ( x) P f 因此P( x)近似代替 ( x)必然存在着误差 f
整体误差的大小反映了插值函数的好坏
成立，则称 P ( x ) 为 f ( x ) 的插值函数
称点 xi , i 0,1,2,, n为插值节点
称区间 a , b]为插值区间 [

第2章插值法

第2章插值法
的n次插值多项式，则对于任何 xa，,b有
Rn (x)
f (n1) ( )
(n 1)!
n1
(
x)
（2.9）
x
其中 n1(x) n (x xi ) , (a,且b)依赖于 。
证明 点都是
由插i值0 条件
知
的零点，故可设Pn(xi)f(xi)
Rn (xi ) 0(i 0,，1,即插, n值) 节
当复杂，使用起来很不方便。面对这些情况，总希望 根据所得函数表（或结构复杂的解析表达式），构造
某个简单函数P(x)作为 的近似。
插值法是解决此类问题的一种比较古老的、
然而却是目前常用f 的x方法，它不仅直接广泛地
应用于生产实际和科学研究中，而且也是进一 步学习数值计算方法的基础。
4
现在你正浏览到当前第四页，共一百零三页。
（图2-3
例1 已知
分别用线性插值和抛物插值
求
的1值0 。1 0,012 11,1 14 1 42
115
15
现在你正浏览到当前第十五页，共一百零三页。
解 因为115在100和121之间，故取节点x0=100，x1=121相应地有 y0=10，y1=11，于是，由线性插值公式（2.5）可得
L1
(
x)
17
现在你正浏览到当前第十七页，共一百零三页。
输入xi,yi,n,x
j=0,1,```,n
P=1
y=0
k=0,1,```,n
k=j?
否 P=P*(x-xj)(xk-xj)
是
输出x,y
图2-4
y=y+P*yk
18
现在你正浏览到当前第十八页，共一百零三页。
lk (x)

第2章1-4节 插 值 法

第2章1-4节 插 值 法

12
图2-3
13
2.
n次插值多项式
根据插值的定义
Ln ( x j ) y j
Ln (x) 应满足
( j 0,1, , n).
为构造 L
n
( x)，
先定义 n 次插值基函数.
14
定义1 若
n 次多项式 L j ( x) ( j 0,1, , n) 在 n 1 个节点
x0 x1 xn
b, Ln ( x)
( n1)
定理2 设 f
(n)
( x)
( x ) 在 ( a, b) 内
存在，节点 a x0 x1 xn
是满足条件
的插值多项式，则对任何 x [a, b] ，插值余项
Rn ( x) f ( x) Ln ( x) f
( n 1
( )
(n 1)!
11
显然，lk (x) 及 lk 1 ( x) 也是线性插值多项式，在节点 xk 及 上满足条件
lk ( xk ) 1, lk 1 ( xk ) 0, lk ( xk 1 ) 0, lk 1 ( xk 1 ) 1,
xk 1
称
lk (x) 及 lk 1 ( x) 为线性插值基函数， 图形见图2-3.
( xk 1 , yk 1 )
的直线. 如图2-2.
图2-2
10
由
L1 ( x)
的几何意义可得到表达式
yk 1 y k xk 1 xk ( x xk )
L1 ( x ) yk
（点斜式）， （两点式），
L1 ( x )
xk 1 x xk 1 xk
yk
x xk xk 1 xk

第2章_插值法

56
13.214 285 71

175 13.228756555322952...
考虑通过 + 1个节点0 < 1 < ⋯ < 的次插值
多项式 ()，满足条件
= ,
= 0,1, … ,
希望找到 li(x)，i = 0, …, n, 使得
= ; = ,
n次插值多项式, 插值节点为{ xi }in 0 [ a , b],则x [ a , b],有
f ( n 1) ( )
Rn (x )
n 1 ( x)
Lagrange型余项
(n 1)!
n
其中 n 1 ( x ) ( x xi ) , ( a , b) , 且依赖于 x.
满足条件P(xi) = f(xi) (i = 0, … n)。 P(x) 称
为f(x) 的插值函数。
P(x) f(x)
x0
x1
x2
x
x3
x4
定理1：设插值节点 ≠ ( ≠ )，则满足条件
= , = 0,1, … , 的插值多项式
= 0 + 1 + ⋯ +
− , , + 线性无关。
二次插值多项式
= − − + + + + ()
满足 = ( = − , , + )
例1:
已知 f ( x )满足 f (144) 12 , f (169) 13, f ( 225) 15
i 0
一次及二次差值余项
1 ′′
1 = − 0 − 1 ,

计算方法—插值法 (课堂PPT)


7
1 1
2 5
4 25
8 125
aa32
4
35
则，
解方程组得a0=10,a1=5,a2=-10,a3=2 即P3(x)=10+5x-10x2+2x3
当n=20,在109次/秒的计算机上计算需几万年！
.
2020/4/2
12
2.2 拉格朗日插值
2-2 线性插值与抛物插值
Chapter2 插值法
第二章 插 值 法
（ Interpolation） 2.1 引言
2.2 拉格朗日插值
2.3 均差与牛顿插值公式
Chapter2 插值法
2.4 埃尔米特插值
2.5 分段低次插值
2.6 三次样条插值
.
2020/4/2
1
2.1 引言
Chapter2 插值法
表示两个变量x,y内在关系一般由函数式 y=f(x)表达。但在实际问题中的函数是多种多 样的,有下面两种情况：
几何意义:L2(x)为过三点(x0,y0), (x1,y1), (x2,y2)的抛物线。
方法：基函数法，构造基函数l0(x), l1(x), l2(x) (三个二次式)
使L2(x)= y0l0(x)+y1l1(x)+y2l2(x)满足插值条件。 6 4 4 4 4 4 4 7 4 4 4 4 4 48
.
2020/4/2
15
2.2 拉格朗日插值
Chapter2 插值法
问题的提法： 已知y=f(x)的函数表，x0, x1, x2为互异节
x x0 x1 x2 y y0 y1 y2
点，求一个次数不超过2的多项式 L2(x)=a0+a1x+a2x2 ：L2(x0)=y0, L2(x1)=y1, L2(x2)=y2

第二章插值与拟合


1 不为零。
xn
n xn xn
实 用 测 量 数 据 处 理 方 法
中 南 大 学
三、线性插值
假定已知区间[xk, xk+1] 的端点处的函数值 yk=f(xk), yk+1=f(xk+1),要求线性插值多项式 L1(x),使它满足 L1(xk)=yk
L1(xk+1)=yk+1
则L1(x)的表达式可按下式给出：
实 用 测 量 数 据 处 理 方 法
中 南 大 学
l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k , k 1) l k ( x k ) 1, l k ( x j ) 0( j k 1, k 1) (28) l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k 1, k ) 满足（28 ）式的插值基函数很容 易求出的，例如求 l k 1 ( x)，因为它有两个零点 k 和x k 1，故可表达为： x l k 1 ( x) A( x x k )(x x k 1 ) 其中A为待定系数可由 k 1 ( x k 1 ) 1定出： l 1 A ( x k 1 x k )(x k 1 x k 1 ) ( x x k )(x x k 1 ) 于是l k 1 ( x)＝ ，同理可得 ( x k 1 x k )(x k 1 x k 1 ) ( x x k－1 )(x x k 1 ) ( x x k 1 )(x x k ) l k ( x)＝ ，l k 1 ( x)＝ ( x k x k－1 )(x k x k 1 ) ( x k＋1 x k 1 )(x k 1 x k )
解：2、抛物插值

计算方法(2)-插值法




2
2
yk1 2

f (xk

h
2
),
y
k

1 2

f (xk

h) 2
21
3.牛顿向后插值公式
Nn (xn

th)

yn

tyn

t(t 1) 2!
2
yn



t(t

1)


(t n!

n

1)

n
yn
(t 0)
插值余项
Rn
(xn

th)

t(t
1) (t (n 1)!
Nn (x0

th)

y0

ty0

t(t 1) 2!
2
y0Leabharlann 插值余项t(t

1)


(t n!

n

1)
n
y0
Rn (x0

th)

t(t
1) (t (n 1)!
n)
h n1
f
(n1) ( ),
(x0 , xn )
20
二.向后差分与牛顿向后插值公式
杂.

根据f(x)函数表或复杂的解析表达式构
造某个简单函数P(x)作为f(x)的近似.
2
2.问题的提法
1)已知条件 设函数y f (x)在区间[a,b]上
连 续, 且 在n 1个不 同点a x0 , x1, , xn b 上 分 别 取 值y0 , y1, , yn
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

l0 (x)
=
(x ( x0
-
x1 )(x - x2 ) x1 )(x0 - x2 )
l1 (x)
=
(x ( x1
-
x0 )(x - x2 ) x0 )(x1 - x2 )
2
L2( x ) = i=0 li ( x) yi
l2( x)
=
(x ( x2
-
x0 )( x - x1 ) x0 )( x2 - x1 )
抛物线插值
§2.2 Lagrange Polynomial
n1
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
n
Pn ( x ) =
i=0
li ( x )
y i
，则显然有Pn(xi)
=
yi
。
li(x)
每个 li 有 n 个根 x0 … xi … xn
n
li (x) = Ci (x - x0)...(x - xi )...(x - xn) = Ci (x - xj )
( x0 ) = = ( xn ) = 0
(n1) ( x ) = 0, x (a, b)
§2.2 Lagrange Polynomial
Rn(x) 至少有 n+1 个根
n
Rn(x) = K(xΒιβλιοθήκη (x - xi )i=0 n
任意固定 x xi (i = 0, …, n), 考察 (t ) = Rn (t ) - K ( x ) (t - xi )
P1 ( x)
=
y0
y1 x1
-
y0 x0
(x
-
x0 )
= x - x1 x0 - x1
y0 +
x - x0 x1 - x0
1
y1 = i=0 li ( x) yi
线性插值
l0(x)
l1(x)
§2.2 Lagrange Polynomial
n = 2 已知 x0 , x1 , x2; y0 , y1 , y2 ，满足 f ( x0 ) = y0 , f ( x1 ) = y1 , f( x2 ) = y2 ，写出二次拉格朗日插值 多项式：
(n 1) !
Rn( x) =
f (n1) ( x ) (n 1) !
n
(x - xi )
i=0
§2.2 Lagrange Polynomial
注： 通常不能确定 x , 而是估计 f (n1)( x) , Mn1 x(a,b)
将
M n1 (n 1)!
n
| x - xi |
i=0
作为误差估计上限。
i=0
(x)有 n+2 个不同的根 x0 … xn x
(n1) ( x ) = 0, x (a, b)
注意这里是对 t 求导
f (n1) ( x ) - L(nn1) ( x ) - K ( x )(n 1) ! =
R ( n1) n
(
x
)
-
K
(
x
)
(n 1) !
K(x) =
f (n1) ( x )
多项式
g(x) f(x)
x0
x1
x2
x
x3
x4
§2.2 拉格朗日多项式 /* Lagrange Polynomial */
求 n 次多项式 Pn ( x) = a0 a1 x an xn 使得
Pn ( xi ) = yi , i = 0, ... , n
条件：无重合节点，即 i j xi x j
第二章 插值法
/* Chapter 2 Interpolation */
§2.1 多项式插值 /* Polynomial Interpolation */ 当精确函数 y = f(x) 非常复杂或未知时，在一 系列节点 x0 … xn 处测得函数值 y0 = f(x0), … yn = f(xn)，由此构造一个简单易算的近似函 数 g(x) f(x)，满足条件g(xi) = f(xi) (i = 0, … n)。这里的 g(x) 称为f(x) 的插值函数。最常 用的插值函数是 …?
当 f(x) 为任一个次数 n 的多项式时， f (n1)( x) 0,
可知 Rn ( x) 0 ，即插值多项式对于次数 n 的多项式 是精确的。
注： • 小的区间上插值有利于减少误差； • 依靠增多插值节点不一定能减少误差； • 多项式插值，外推误差可能要比内插误差大。
定理 (唯一性) 满足 P( xi ) = yi , i = 0, ... , n 的 n 阶插值多
项式是唯一存在的。 证明：
反证：若不唯一，则除了Ln(x) 外还有另一 n 阶多项 式 Pn(x) 满足 Pn(xi) = yi 。 考察 Qn( x) = Pn( x) - Ln( x) , 则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn
注：若不将多项式次数限制为 n ，则插值多项式不唯一。
n
例如 P( x) = Ln ( x) p( x) ( x - xi ) 也是一个插值 i=0
多项式，其中 p( x)可以是任意多项式。
§2.2 Lagrange Polynomial
➢ 插值余项 /* Remainder */ 设节点 a x0 x1 xn b ，且 f 满足条件 f C n[a,b] , f (n1)在[a , b]内存在, 考察截断误差 Rn( x) = f ( x) - Ln( x)
Rolle’s Theorem: 若(x) 充分光滑， ( x0 ) = ( x1 ) = 0 ，则 存在 ( x0 , x1 ) 使得 ( ) = 0。
推广：若 ( x0 ) = ( x1 ) = ( x2 ) = 0
0 ( x0 , x1 ), 1 ( x1 , x2 )
使得 (0 ) = (1 ) = 0 (0 , 1 ) 使得 ( ) = 0
n= 1
已称知为x拉0 氏, x基1 ;函y0数, y1/*，La求graPn1g(exB) =asais0 */，a1 x 使得
P满1( 足x0 )条= 件y0 l,i(Px1j)(=x1 )ij=/*yK1 ronecker Delta */
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
ji
j=0
li (xi ) = 1
Ci
=
ji
( xi
1 -
xj )
与 节点 有关，而与 f 无关
Lagrange Polynomial
li ( x) =
n ji
(x- xj) (xi - x j )
j=0
n
Ln ( x) = li ( x) yi i=0
§2.2 Lagrange Polynomial