网络图工作时间参数的计算步骤

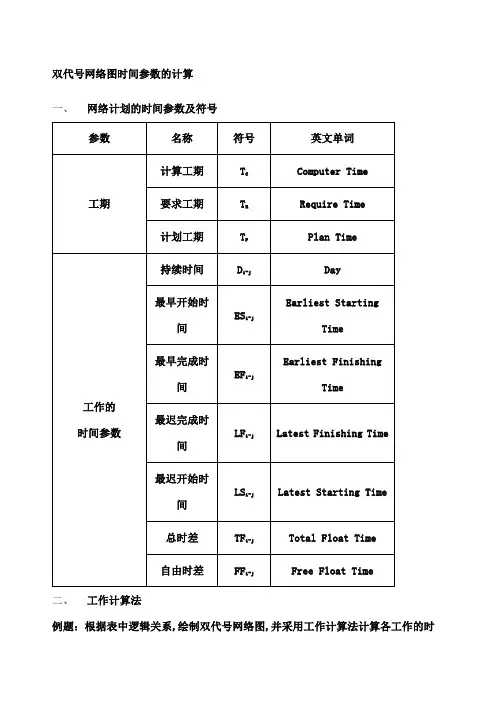
双代号网络图时间参数的计算一、网络计划的时间参数及符号二、工作计算法例题：根据表中逻辑关系,绘制双代号网络图,并采用工作计算法计算各工作的时间参数;一工作的最早开始时间ESi-j--各紧前工作全部完成后,本工作可能开始的最早时刻;二工作的最早完成时间EFi-jEFi-j ＝ESi-j+ Di-j1．计算工期Tc等于一个网络计划关键线路所花的时间,即网络计划结束工作最早完成时间的最大值,即Tc ＝max｛EFi-n｝2．当网络计划未规定要求工期Tr 时, Tp＝Tc3．当规定了要求工期Tr 时,Tc≤Tp,Tp≤Tr--各紧前工作全部完成后,本工作可能完成的最早时刻;三工作最迟完成时间LFi-j1．结束工作的最迟完成时间LFi-j ＝Tp2. 其他工作的最迟完成时间按“逆箭头相减,箭尾相碰取小值”计算; --在不影响计划工期的前提下,该工作最迟必须完成的时刻;四工作最迟开始时间LSi-jLSi-j ＝LFi-j－Di-j--在不影响计划工期的前提下,该工作最迟必须开始的时刻;五工作的总时差TFi-jTFi-j ＝LSi-j－ESi-j或TFi-j＝LFi-j－EFi-j--在不影响计划工期的前提下,该工作存在的机动时间;六自由时差FFi-jFFi-j ＝ESj-k－EFi-j--在不影响紧后工作最早开始时间的前提下,该工作存在的机动时间; 作业1：根据表中逻辑关系,绘制双代号网络图;作业2：根据表中逻辑关系,绘制双代号网络图;。

网络图的时‎间参数计算‎计算网络计‎划的时间参‎数，是编制网络‎计划的重要‎步骤，可以说，网络计划如‎果不计算时‎间参数，就不是一个‎完整的网络‎计划。

(一)计算时间参‎数的目的1.确定关键线‎路网络图从起‎点节点顺着‎箭头方向顺‎序通过一系‎列箭杆和节‎点，最后到达终‎点节点的一‎条条道路称‎为线路。

关键线路就‎是网络图中‎最重要、需时最长的‎线路。

关键线路上‎的工序叫做‎关键工序。

关键线路的‎总长度所需‎时间叫做总‎工期，一般用方框‎“口”标在终点节‎点的右方。

关键线路的‎工期决定整‎个工期的长‎短，它拖后一天‎，总工期就相‎应拖后一天‎；它提前一天‎，则总工期有‎可能提前一‎天。

关键线路最‎少必有一条‎，也可能有多‎条。

一般来讲，安排得好的‎计划，往往出现有‎关零件同时‎完成，组成部件；有关部件同‎时完成，进行总装配‎的情况。

这样，关键线路就‎不是一条了‎。

愈好的计划‎，关键线路愈‎多，作领导的更‎要全面加强‎管理，不然一个环‎节脱节会影‎响全局。

多条关键线‎路也可以作‎为劳动竞赛‎的依据。

关键线路在‎网络图上可‎以用带箭头‎的粗线、双线或红线‎表示。

2．确定非关键‎线路上的机‎动时间(或称浮动时‎间、富裕时间)在一份网络‎图中，不是关键线‎路的线路称‎非关键线路‎。

非关键线路‎上的工序，由于前后工‎序及平行工‎序的作用，使得它被限‎制在某一段‎时间之内必‎须完成，而当该工序‎的工作持续‎时间小于被‎限制的这段‎时间时，它就存在富‎裕时间(机动时间)，其大小是一‎个差值，因此也称为‎“时差”。

时差只能是‎正值或者为‎零。

一项工程的‎网络图画出‎来之后，如果要想提‎前完成，则要想方设‎法压缩关键‎线路的工期‎。

为达此目的‎，要调动人力‎物力等资源‎，要么从外部‎调整，要么从内部‎调整。

一般认为，从内部调整‎是较为经济‎的。

从内部调，就是从非关‎键线路上调‎。

调多少，则要看非关‎键线路上富‎裕时间的“富裕”程度，即时差有多‎少。

2（一）．网络图中的六个时间参数（重点）网络图中的时间参数主要有六个：最早开始时间；最早完成时间；最迟开始时间；最迟完成时间；总时差和自由时差。

各时间参数的含义如下。

(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后，本工作有可能开始的最早时刻。

(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后，本工作有可能完成的最早时刻。

工作的最早完成时间等于工作最早开始时间与其持续时间之和。

(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。

(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。

工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。

(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下，本工作可以利用的机动时间。

(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。

3．双代号网络图中时间参数的计算(1)时间参数计算数学模型：下面取一网络片断(图9-24)作为计算简图。

令整个计划的开始时间为第0天，则：工作最早开始时间等于其紧前工作最早完成时间的最大值。

令整个计划的总工期为一常数，则：工作最迟完成时间等于其紧后工作最迟开始时间的最小值。

在网络计划中，总时差最小的工作为关键工作。

特别地，当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作。

由于工作的自由时差是总时差的构成部分，所以，当工作的总时差为零时，其自由时差必然为零。

即：如果网络计划中工作数量比较多，一般用项目管理软件进行计算。

如果数量不多也可用手工进行计算。

(2)计算步骤。

双代号网络计划时间参数的计算方法自认为对双代号网络图的知识掌握的差不多，也能够理解；只是在遇到这六个时间参数的时候，还是有些发怵，今天重新把这六个参数捋了捋，总结如下：1、最早开始时间、最早完成时间：从网络计划的起点节点开始，顺着箭头方向依次进行；以网络计划起点为开始节点的工作，当未规定其最早开始时间时，其最早开始时间为零；有多个紧前工作的工作，其最早开始时间等于其紧前工作最早完成时间的最大值。

2、最迟开始时间、最迟完成时间：从网络计划的终点节点开始，顺着箭头方向依次进行；以网络终点节点为完成节点的工作，其最迟完成时间等于网络计划的计划工期，即要先找出关键线路，求出计划总工期作为最后一项工作的最迟完成时间；有多个紧后工作的工作，其最迟完成时间等于其紧后工作最迟开始时间的最小值。

3、总时差：不影响总工期的时差，等于该工作最迟完成时间与最早完成时间之差，或该工作最迟开始时间与最早开始时间之差；总时差最小的工作为关键工作，当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作；同一条线路上的总时差相等（同一条线路都可以共用的时间，谁用了是谁的，不影响总工期）。

4、自由时差不影响紧后工作的时间；对于有多个紧后工作的工作，其自由时差等于本工作之紧后工作最早开始时间-本工作最早完成时间所得之差的最小值；无紧后工作的工作，也就是以网络计划重点节点为完成节点的工作，其自由时差等于计划工期与本工作最早完成时间之差；对于网络计划中以重点节点为完成节点的工作，其自由时差与总时差相等；只有一项紧前工作的紧前工作，该紧前工作的自由时差为0；自由时差小于等于总时差，总时差为零自由时差必为0 。

呵呵，本来想用通俗的语言解释一下，可写下来还是有点绕，我觉得这东西贵在理解，好像只是专家们为了考试罗列了一些概念，把简单的问题弄复杂了；没办法为了考试，慢慢理解吧。

二、搭接网络计划时间参数的计算单代号搭接网络计划时间参数的计算与前述单代号网络计划和双代号网络计划时间参数的计算原理基本相同。

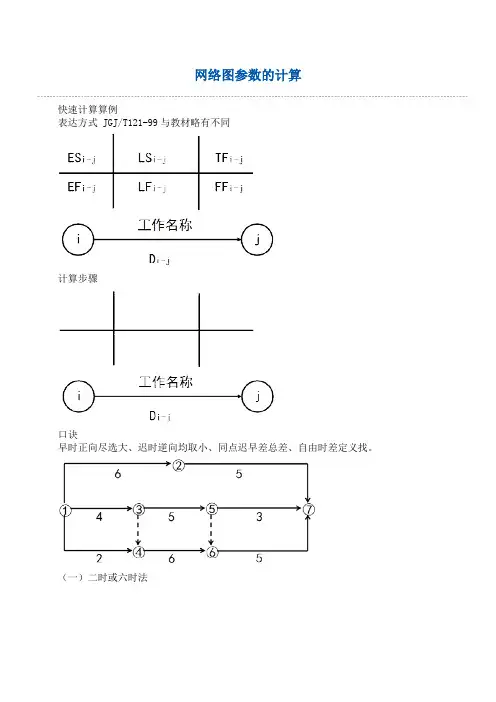
网络图参数的计算快速计算算例表达方式 JGJ/T121-99与教材略有不同计算步骤口诀早时正向尽选大、迟时逆向均取小、同点迟早差总差、自由时差定义找。

（一）二时或六时法二时标注法——只标注各项工作的最早开始时间和最迟开始时间。

（二）按节点计算法节点的最早时间——以该节点为开始节点的各项工作的最早开始时间ETi；节点的最迟时间——以该节点为完成节点的各项工作的最迟完成时间LTj。

图例：1.计算节点的最早时间和最迟时间计算节点的最早时间节点最早时间的计算应从网络计划的起点节点开始，顺着箭线方向依次进行。

网络计划起点节点，如未规定最早时间时，其值等于零。

其他节点的最早时间计算：ETj ＝max{ETi＋Di－j} （3－12）计算工期等于终点节点的最早时间：T c ＝ETn（3－13）确定网络计划的计划工期计算节点的最迟时间节点最迟时间的计算应从网络计划的终点节点开始，逆着箭线方向依次进行。

终点节点的最迟时间等于计划工期： LTn ＝Tp（3－15）其他节点的最迟时间：LTi ＝min{LTj－Di－j} （3－16）2.根据节点的最早时间和最迟时间判定工作的六个时间参数工作的最早开始时间=该工作开始节点的最早时间ESi-j = ETi工作的最早完成时间=该工作开始节点的最早时间+该工作的持续时间EFi-j = ETi+ Di-j工作的最迟完成时间=该工作完成节点的最迟时间LFi-j = LTj工作的最迟开始时间=该工作完成节点的最迟时间 -该工作的持续时间LSi-j = LTj- Di-j总时差＝该工作完成节点的最迟时间－该工作开始节点的最早时间－持续时间TFi-j = LTj-ETi-Di-j自由时差＝该工作完成节点的最早时间－该工作开始节点的最早时间－持续时间。

FFi-j = ETj-ETi-Di-j3.确定关键线路和关键工作在双代号网络计划中，关键线路上的节点称为关键节点。

关键工作两端的节点必为关键节点，但两端为关键节点的工作不一定是关键工作。

⽹络图时间参数的计算⽅法，再上⼀课吧⽬的在于确定⽹络图上各项⼯作和各个节点的时间参数，为⽹络计划的优化、调整和执⾏提供明确的时间概念。

主要包括：各个节点的最早时间（ET）和最迟时间（LT）；主要包括：各项⼯作的最早开始时间（ES）、最早结束时间(EF)、最迟开始时间(LS)、最迟结束时间(LF)；各项⼯作的有总时差（TF）和⾃由时差（FF）。

⽹络图时间参数的计算⽅法主要有：分析计算法、图上计算法、表上计算法、矩阵计算法和⽹络图时间参数的计算⽅法主要有：电算法。

1) 起点节点i；2）节点j只有⼀条内向箭线时；3）节点j有多条内向箭线时候。

1）节点i的最迟时间LTi 从⽹络图终点节点开始，逆着箭线⽅向逐项计算。

2）终点节点i的最迟时间等于终点节点i的最早时间；LTn=ETn3）节点i有多条外向箭线时。

1) 本⼯作最早开始时间=本⼯作起始节点最早时间2) 本⼯作最早完成时间=本⼯作最早开始时间+本⼯作持续时间3) 本⼯作最迟完成时间=本⼯作尾节点最迟时间4) 本⼯作最迟开始时间=本⼯作尾节点最迟时间-本⼯作持续时间5) ⼯作总时差=本⼯作最迟开始时间-本⼯作最早开始时间6) ⼯作⾃由时差=本⼯作尾节点最早时间-本⼯作最早结束时间1) 本⼯作最早开始时间=本⼯作起始节点最早时间2) 本⼯作最早完成时间=本⼯作最早开始时间+本⼯作持续时间3) 本⼯作最迟完成时间=本⼯作尾节点最迟时间4) 本⼯作最迟开始时间=本⼯作尾节点最迟时间-本⼯作持续时间5) ⼯作总时差=本⼯作最迟开始时间-本⼯作最早开始时间6) ⼯作⾃由时差=本⼯作尾节点最早时间-本⼯作最早完成时间。

施工网络图参数计算技巧
1、工作的最早开始时间（ES）顺着箭线的方向来计算，当有多条线路到达这项工作的时候，选取数值的最大值；（注意为加上各紧前工作的持续时间后的最大值）；
最早完成时间EF=ES+D (D为本项工作的持续时间)；
2、工作的最迟完成时间（LF），逆着箭线方向来计算，遇到多条线路到达这项工作时，选取数值的最小值。

（注意先应计算总工期，即为和终点节点相连的工作的最迟完成时间。

中间工作为减去紧后工作持续时间后的最小值）；
最迟开始时间LS=LF—D (D为本工作的持续时间)；
3
本公式中，持续时间D=EF—ES=LF—LS TF=LS—ES=LF—EF
记忆为：上—下=持续时间（D），右—左=总时差（TF）
后上1—前下1=自由时间（FF）
即为紧后工作的最早开始时间减去本工作的最早完成时间；
4、参数计算时可先从前往后计算工作最早开始时间（ES）和工作最早完成时间（EF）。

和起点节点相连的工作，最早开始时间都相等，且最早开始时间（ES）=0
5、然后从后往前计算工作最迟完成时间（LF）和工作最迟开始时间（LS）。

和终点节点相连的工作，最迟完成时间（LF）和最早开始时间（EF）都相等，且最迟完成时间（LF）=总工期（T）；自由时差（FF）=总时差（TF）；。

6、关键线路中：ES=LS EF=LF TF=LS—ES=LF—EF=0 FF=0；。

双代号网络图六个时间参数的简易计算方法之南宫帮珍创作一、非常有用的要点：任何一个工作总时差≥自由时差自由时差即是各时间间隔的最小值（这点对六时参数的计算非经常使用用）关键线路上相邻工作的时间间隔为零, 且自由时差=总时差在网络计划中, 计算工期是根据终点节点的最早完成时间的最年夜值二、双代号网络图六时参数总结的计算步伐（比书上简单多了）①②t 过程步伐一：1．A 上再做A 下2．做的方向从起始工作往结束工作方向；关键工作：总时差最小的工作最迟开始时间—最早开始时间（min ）最迟完成时间—最早完成时间（min ）3．起点的A上＝0, 下一个的A上＝前一个的A下；当遇到多指向时, 要取数值年夜的A下A上4．A下=A上+t过程（时间）步伐二：1．B下再做B上2．做的方向从结束点往开始点3．结束点B下=T（需要的总时间=结束工作节点中最年夜的A下）结束点B上=T-t过程（时间）4．B下=前一个的B上（这里的前一个是从终点起算的）；遇到多指出去的时, 取数值小的B上B下tB上=B下—t过程（时间）步伐三：总时差=B上—A上=B下—A下如果不相等, 你就是算错了步伐四：自由时差=紧后工作A上（取最小的）—本工作A下例：6 8 2 * 9 11 2=0 13 15 2*11 12 114 15 1紧后工作A上有9和11取小值9,？=9-9（本工作的A下）=0总结起来四句话：1．最早时间从起点开始, 最早开始＝紧前最早结束的max 值；2．最迟时间总终点开始, 最迟完成＝紧后最迟开始的min 值；3．总时差＝最迟－最早；4．自由时差＝紧后最早开始的min值－最早开始注：总时差＝自由时差＋紧后总时差的min值。

双代号网络图时间参数计算网络图时间参数计算的目的是确定各节点的最早可能开始时间和最迟必须开始时间，以及各工作的最早可能开始时间和最早可能完成时间，最迟必须开始时间和最迟必须完成时间，各工作的总时差和自由时差，以便确定整个计划的完成日期、关键工作和关键线路，从而为网络计划的执行、调整和优化提供科学的数据。

时间参数的计算可采用不同方法，如图上作业法、表上作业法和电算法等，这里主要介绍图上作业法和表上作业法。

1.各项时间参数的符号表示图1∙1时间参数关系简图设有线路h~Hfjfk,则：D i.——工作i—j的施工持续时间；Dj——工作i—/的紧前工作h-i的施工持续时间；D hk——工作i—/♦的紧后工作/一k的施工持续时间；T iε——节点①最早时间；T；——节点①最迟时间;里——工作i-∕的最早开始时间；——工作i-j的最早完成时间；坐——工作i-∕的最迟开始时间；T£——工作，一/的最迟完成时间；用——工作，一/的总时差；电——工作，一/的自由时差；2.时间参数间的关系分析图1-1这条线路，可以得出如下结论:睛=T i εT 苔=需+ %丐=T-* =哨-0T3 .图上作业法当工作数目不太多时•，直接在网络图上进行时间参数的计算十分方便。

由于双代号 网络图的节点时间参数与工作时间参数紧密相关，因此，在图上进行计算时.，通常只需 标出节点（或工作）的时间参数。

现以图1-2为例介绍图上作业法的步骤：（I ）计算各个节点的最早时间7"节点的最早时间就是该节点前面的工作全部完成，后面的工作最早可能开始的时间。

计算节点的最早开始时间应从网络图的起点节点开始，顺着箭线方向依次逐项计算，直 到终点节点为止。

计算方法是：先假定起点节点①的最早时间为零，即7丁=0;中间节 点的最早时间为该节点前各紧前工作最早完成时间中的最大值。

根据公式（1-2）,工作 的最早完成时间为工作的最早开始时间（即工作的开始节点的最早时间）加上工作的持 续时间，故：T=ma⅛" + %∙} （1-5）在图1-2中，各节点的最早时间计算如下:(1-1) (1-2) (1-3) (1-4)图1・2图上作业法示意图4^=7]E+D1,2=0+7=7*=7]E + %=0 + 4 = 47]E+D1,4=0+4=4'乃= max<琛+ 2 .4 =7 + 2 = 91 = 9* +。