快速绘制梁的剪力图和弯矩图

怎样快速绘制剪力图和弯矩图3毛和业(黔南职业技术学院机电系,贵州,都匀558022)摘　要:在工程构件中,最常见的变形形式是弯曲变形和弯扭组合变形。

它们的强度计算必须以剪力图和弯矩图的绘制来找到危截面为前提,而这一绘制过程复杂,计算量大。

根据各种载荷的剪力图和弯矩图规律对这一过程进行简化,可找到一种学生易于掌握,且准确率高的方法。

关键词:剪力图;弯矩图;绘制;快速中图分类号:T B23 文献标识码:B 文章编号:1005-6769(2005)03-0081-03How to D raw the Shear i n g Force D i a gram and Bend i n g M o m en t D i a gram Rap i dlyMAO He -ye(Mechanical and Electr onic Depart m ent,Q iannan Vocati onal and Technical College,Duyun 558022,China )Abstract:I n structural me mbers,the defor mati on is usually caused by bending or by a combinati on of bending and t orsi on .W e calculate their strength based on finding the critical secti on by drawing the shearing force diagra m and bending moment diagra m that is relatively comp lex and needs l ots of work .Theref ore,according t o the regulati ons of shearing f orce diagra m and bending moment diagra m caused by different l oad models,this paper si m p lifies the p r ocess and finds an easy and accurate method .Key words:shearing f orce diagra m;bending moment diagra m;dra w;rap id1　引言 《工程力学》是工科各专业的一门重要的技术基础课,特别对于机电类专业,学生学习质量的好坏,对后续课程的学习,如《机械原理》《机械零件》《汽车理论》等乃至于对今后的工作至关重要。

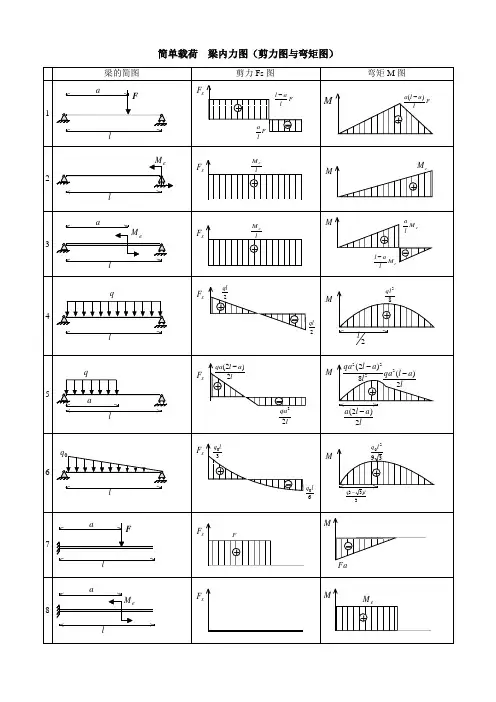
简单载荷 梁内力图（剪力图与弯矩图）梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注：外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件（约束端无集中载荷）固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰∙=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

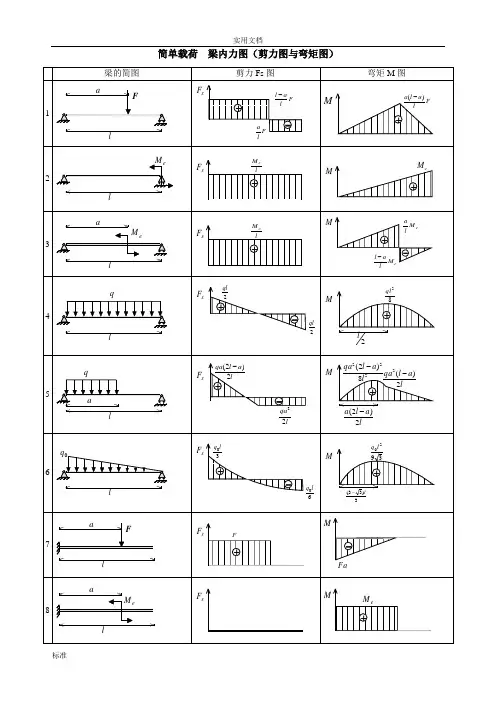
简单载荷梁内力图（剪力图与弯矩图）表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

实用文档2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

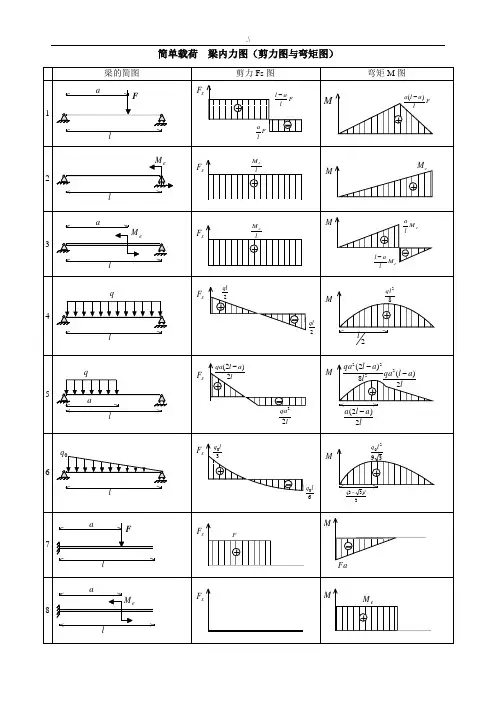
简单载荷梁内力图（剪力图与弯矩图）表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

.\2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

图1外伸梁AB承受图F B=3.8kN（↑）画剪力图。

从左到右画，对于平衡问题，剪到零结束。

A截面作用有向下的集中力，所以剪力图要向下突变，从零开始，突变值3kN，AC段没有分布荷载作用，线。

C截面有向上的集中力作用，图2剪力图图3弯矩图到零结束。

A 截面是自由截面且没有集中力偶作用，所以弯矩为零。

C 截面弯矩即AC 段-3kN ·m 。

AC 段没有分布荷载，弯矩CD 段有均布荷载作用，弯矩图抛物均布荷载箭头向下，所以抛物线向下凸。

画抛个截面，分别是均布荷载的起端、末端及剪力为零处对应的弯矩值即抛物线顶点。

由剪力图可求得剪力为零处的位置，根据积分关系就能求得该处的弯矩值为1.41kN ·弯矩值为-2.2kN ·m 。

D 截面处有集中力偶作用，矩图要发生突变。

集中力偶的方向是顺时针，而下，所以弯矩图向下突变，突变值到3.8kN ·m 。

DB 段没有分布荷载作用，图是斜直线。

B 截面是铰接处，没有集中力偶作用，弯矩为零。

标明弯矩的单位及正负号总结本文以横向分布力集度与剪力、弯矩的微分关系为基础，总结归纳了几种荷载作用下剪力图和弯矩图的特征，具体讲述了如何用简易法画内利用它们之间的积分关系，可由内力图面积快速求出控制截面的内力值。

掌握这些特征，就可以不用写内力方程而根据外力直接画出相应的内力图，简单、高效。

参考文献［1］邓宗白,陶阳,吴永端.材料力学［M ］.北京2013.［2］刘鸿文.材料力学(Ⅰ)［M ］.北京:高等教育出版社［3］孙训方.材料力学［M ］.(第5版)北京:高等教育出版社2009.. All Rights Reserved.。

快速绘制梁的剪力图和弯矩图哎呀，今天咱们来聊聊一个很有意思的话题：快速绘制梁的剪力图和弯矩图。

这可不是啥高深莫测的技术活儿，就是让大家了解一下梁的结构特点，然后用简单的方法画出它的受力情况。

别看这个过程好像挺复杂的，其实只要掌握了一定的技巧，就能轻松搞定！咱们得了解一下梁的基本结构。

梁是建筑物中常见的一种构件，它的主要作用是承受垂直于其长度方向的荷载，将这些荷载传递到支撑结构上。

梁通常由两个平行的钢板或混凝土板组成，这两个板之间的距离叫做梁的宽度。

梁的长度可以是任意值，但通常会根据建筑物的实际需求进行设计。

接下来，我们来说说如何绘制梁的剪力图。

剪力图是一种表示梁在不同位置受到剪力作用时的力的分布情况的图形。

要画出剪力图，我们需要知道梁的几何尺寸、材料的抗剪强度以及荷载的大小。

有了这些信息，我们就可以用一些简单的公式来计算梁在不同位置受到的剪力大小了。

我们要把梁划分成若干个小的单元，这样才能更好地观察和分析梁的受力情况。

一般来说，我们可以把梁划分成若干个矩形或梯形的小单元。

然后，我们可以用一些公式来计算每个小单元受到的剪力大小。

这些公式包括：1. 矩形单元的剪力大小 = 矩形面积× 材料抗剪强度× 剪切模量2. 梯形单元的剪力大小 = (梯形面积× 材料抗剪强度× 剪切模量) ÷ 2有了这些公式，我们就可以开始画剪力图了。

我们在纸上画出一个坐标系，然后用坐标轴表示梁的长度和位置。

接着，我们可以用不同的颜色或线条来表示不同位置的剪力大小。

例如，我们可以用红色表示剪力较大的区域，用蓝色表示剪力较小的区域。

我们可以在图上加上一些注释，说明各个区域的具体含义。

现在，我们再来说说如何绘制梁的弯矩图。

弯矩图是一种表示梁在不同位置受到弯曲作用时的力的分布情况的图形。

要画出弯矩图，我们同样需要知道梁的几何尺寸、材料的抗弯强度以及荷载的大小。

有了这些信息，我们就可以用一些简单的公式来计算梁在不同位置受到的弯矩大小了。

利用口诀绘制梁的剪力图与弯矩图在高教版《汽车机械基础》中，梁弯曲时的剪力图与弯矩图的绘制方法是一个难点。

本人在教学过程中，发现学生运用常规法绘制剪力弯矩图时，常感到枯燥、繁琐，尤其在列剪力、弯矩方程以及求各特征点的剪力和弯矩值时经常出错，这不但使学生丧失了解决问题的信心，而且此后梁的弯曲强度、刚度等一系列计算无法顺利进行，使教学任务停滞不前。

为了解决上述问题，本人结合相关材料，发现梁上的载荷、剪力与弯矩之间的变化具有一定的规律性。

如果进一步将这些规律总结成口诀，可使计算工作量大大减少，大大提高做题速度，并且不易出错，便于检验。

工程中常见的梁分三种：简支梁、外伸梁和悬臂梁。

梁上载荷有三种常见的基本形式：集中力作用(F或约束反力)，集中力偶作用（M）,以及均布载荷作用（q）。

而梁上是否有均布载荷将直接影响到梁的剪力与弯矩图的绘制效果，也是剪力弯矩图能否正确绘制的关键。

一、无均布载荷梁的剪力弯矩图的绘制口诀示例1：如图1简支梁AB，受力情况及尺寸如图所示，试绘制该梁的剪力图与弯矩图。

第三步：根据剪力、弯矩方程及特征值绘出剪力图和弯矩图。

方法分析：通过绘图过程我们不难看出，无论剪力图还是弯矩图从左到右看有如下特点：1.内力图图形自行封闭。

2.对于该简支梁AC段和CB段，剪力方程都是常数方程，故剪力图都是直线，而且该直线在有集中力作用的地方发生了转折，有明显的突变。

进一步观察不难发现，其突变的值恰好等于集中力的大小，而且突变的方向与集中力方向一致。

3.简支梁各段弯矩方程都是直线方程，弯矩图都是斜直线。

结合剪力图和弯矩图我们看出，斜直线的倾斜方向与剪力图有一定关系：当剪力为正值（图形位于X轴上方）时，斜线斜向下；当剪力图为负值（图形位于X轴下方）时，斜线斜向上，所以，在弯矩图上出现了明显的尖点，尖点的尖突方向与集中力方向一致。

而且，斜直线的斜率（尖点位置弯矩值）恰好等于对应剪力图的面积大小。

因此，我们可以总结出如下口诀：剪力图：无力作用水平线，有力作用有突变（突变值为集中力的大小，突变方向与集中力方向一致）。

口诀法在梁内力图绘制中的应用（苏科大土木学院2020.5）弯矩与剪力有这样的关系：弯矩方程比剪力方程高一阶，弯矩方程的一阶导数是剪力方程，弯矩图的在某个截面的斜率值恰恰就是该截面的剪力。

弯矩与剪力、分布荷载之间的微分积分关系，可作为弯矩图绘制的理论依据。

本文以画梁的内力图为例，淡淡形象教学法在力学教学中的应用。

利用形象的口诀同时将弯矩、剪力与荷载集度问的微分关系及梁的内力图的一些特点，文献中的作者们做了大量工作，这里作汇总如下（部分略有改动）。

（1）黄氏口诀[3]：剪力图口诀：剪力跟随载荷走；均布载荷顺着斜；集中力处随着跳；上下看力的方向，遇到力偶剪力不会变。

（要求从左至右画）。

弯矩图口诀：差值等于Q与轴围图的面积；突变朝着同向矢；曲线突向顺着q；顶点正好对零剪。

特征：分段、突变、直线、曲线。

（2）高氏口诀[4]：均布荷载负，剪力下（右下）斜路．弯矩下（下凸）抛物；均布荷载零，剪力直线平，弯矩斜向行；集中力在梁上现．剪力要突变（顺F方向），弯矩定折转（F作用截面出现折角）；力偶作用面，剪力照常现（左右相同），弯矩要突变（顺时针力偶向下突变）。

最大弯矩可能发生在F，零（剪力为零）、F。

变（剪力变号）和紧靠力偶一侧面。

（3）钱氏口诀[5]：剪力图口诀：没有外力，水平线；均布外力，斜直线；集中外力，有突变；集中力偶，不用变。

剪力、弯矩图的相对应口诀：①你无我平，你平我斜，你斜我弯，弯线顶点你为0；②顺流而下，逆流而上，集中力偶来管上；③上尖角、下尖角，外力指向要看好。

（4）网络口诀（作者不详）。

剪力图口诀:外伸端，自由端，没有集中力取零点。

无力梁段Q水平线，集中力偶同样看，均布荷载Q应为斜线，小q正负定增减，集中力处有突变，左顺右逆画竖线，增多少？降多少？集中横力作参考。

弯矩图口诀:弯矩图，较复杂，对照剪图来画它；自由端，铰支端，没有力偶作零点。

剪图水平弯图斜，剪力正负定增减；天上下雨池水满，向上射出弓上箭。