8.2角的比较导学案

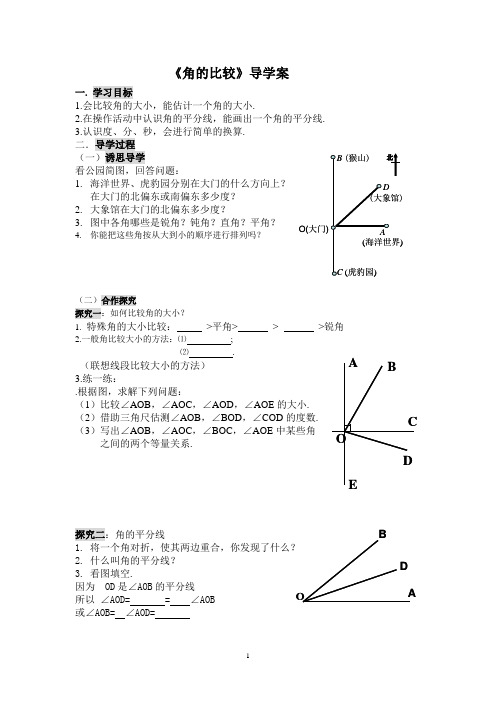
《角的比较》导学案一. 学习目标1.会比较角的大小，能估计一个角的大小.2.在操作活动中认识角的平分线，能画出一个角的平分线.3.认识度、分、秒，会进行简单的换算.二．导学过程（一）诱思导学看公园简图，回答问题：1.海洋世界、虎豹园分别在大门的什么方向上？在大门的北偏东或南偏东多少度？2.大象馆在大门的北偏东多少度？3.图中各角哪些是锐角？钝角？直角？平角？4.你能把这些角按从大到小的顺序进行排列吗？（二）合作探究探究一：如何比较角的大小？1.特殊角的大小比较：>平角> > >锐角2.一般角比较大小的方法：⑴;⑵ .（联想线段比较大小的方法）3.练一练：.根据图，求解下列问题：（1）比较∠AOB，∠AOC，∠AOD，∠AOE的大小. （2）借助三角尺估测∠AOB，∠BOD，∠COD的度数. （3）写出∠AOB，∠AOC，∠BOC，∠AOE中某些角之间的两个等量关系.探究二：角的平分线1.将一个角对折，使其两边重合，你发现了什么？2.什么叫角的平分线？3.看图填空.因为 OD是∠AOB的平分线所以∠AOD= = ∠AOB或∠AOB= ∠AOD=A BCD EOOD BA))O(大门)4．考考你已知，OC 是∠AOB 内部的一条射线，下列所给的条件中不能判定OC 为∠AOB 的平分线的是（ ）A. ∠ AOC= ∠AOBB. ∠AOC+ ∠BOC= ∠AOBC. ∠ AOB=2∠AOCD. ∠AOC= ∠BOC 探究三：认识度、分、秒，并进行简单的换算.自学课本149页图4—17下方的内容，思考并回答： 1.1度、1分及1秒是如何得到的？如何表示？ 2.度、分、秒之间是如何转换的？ 1°= ′ 1′= ″ 1′= ° 1″= ′ 3.计算:(1)1.45°等于多少分?等于多少秒? (2) 1800″等于多少分?等于多少度?（三）快乐达标1.3.15°=____°____′2.已知∠AOB=50°, ∠COB =30°,则∠COA 等于( ) A.20° B.80° C.20°或80° D.不能确定3.如图, ∠ AOC= ∠BOD =90 °. (1)若∠DOC =28°,则 ∠AOB =_____.(2)找出图中相等的角.如果∠DOC ≠28°, 它们还会相等吗?为什么?（四）课堂小结 今天你收获了什么？（五）拓展提高借助一副三角尺的拼摆,你能画出15°、75°的角吗?你还能画哪些度数的角？这些角有什么共同特征?ODC BA21。

《角的比较》学案第一部分课堂练习（一）根据下图，回答下列问题（1）比较∠AOB、∠AOC、∠AOD、∠AOE的大小,并指出其中的锐角、直角、钝角、平角.（2）试比较∠BOC和∠DOE的大小.（3）小亮通过折叠的方法，使OD与OC重合，OE落在∠BOC的内部，所以∠BOC 大于∠DOE.你能理解这种方法吗？（4）请在图中画出小亮的折痕OF，∠DOF与∠COF有什么大小关系？第二部分课堂练习（二）1、下面的式子中，能表示“OC是∠ AOB的角平分线”的等式是（）A、2 ∠ AOC＝∠ BOCB、∠ AOC＝∠ AOBC、∠ AOB＝2∠ BOCD、∠ AOC＝∠ BOC2、已知射线OC是∠AOB的角平分线，你能写出图中各角的关系吗？3、如图OB是∠AOC的平分线，∠COD=2∠AOB，试说明OC是哪一个角的平分线？4、思考：如图：∠AOB=130°∠AOD=30°∠BOC=70°问：OD是∠AOC的平分线吗？OC是∠AOB的平分线吗？为什么？第三部分课堂练习（三）1、按图1填空：1）∠D0B ∠BOC2）∠C0B ∠AOC3）∠D0C＋∠COB ∠BOD4）∠A0B＋∠BOC＝5）∠A0C＋∠COD＝6）∠B0D－∠COD＝7）∠A0D－＝∠A0B2、已知OB是∠AOC的平分线, OD是∠COE的平分线，如果∠AOE=130°, 那么∠BOD是多少度?第四部分能力提升：1、比较大小：32.5° 32°5′（填“＞”、“=”或“＜”）．2、在∠AOB 的内部任取一点C ，作射线OC ，则一定存在（ ）A 、∠AOB ＞∠AOC B 、∠AOB ＞∠BOCC 、∠BOC ＞∠AOCD 、∠AOC ＞∠BOC3、如图，已知∠AOC=90°，∠COB= α ，OD 平分∠AOB则∠COD 等于多少度？（用含α的式子表示）第五部分实践活动：借助一副三角尺，你能画出75 °角吗？15 °呢？你还能画出哪些度数的角？4、5、。

角的比较教案：如何帮助学生理解角的大小关系？一、教学目标1.知识目标：通过教学，帮助学生掌握角的大小关系，理解角度的度量单位等概念。

2.技能目标：培养学生观察、比较、分析的能力，以及对角度问题进行有效解决的能力。

3.情感目标：增强学生的数学兴趣，调动学生的学习积极性，促进学生对数学的深入了解和学习。

二、教学内容本教案主要介绍如何帮助学生理解角的大小关系，主要内容包括：1.角的定义和度量单位。

2.角的基本性质，包括角的大小比较、角的补角和余角、同位角和绝对值等概念。

3.角的测量方法和角度的度量。

4.角度的运用和角的图像表示。

三、教学方法1.视觉化教学法：通过图片、图形和实物等方式来帮助学生直观感受角的大小关系。

2.比较教学法：通过对比不同的角度大小，帮助学生理解角的度量单位和大小比较。

3.互动式教学法：通过举例解题、小组合作等方式，培养学生的分析和解决问题的能力。

四、教学过程1.知识讲解：教师简略介绍角的定义和度量单位，并通过图片和实物让学生感受角的大小和形态。

2.角的比较：教师放映一些具有代表性的角度大小图片，帮助学生感受角度大小的差异，并进行大小比较。

3.互动解题：教师出示几个具有不同角度的图形，让学生分析和解题，比较出它们的角度大小关系。

4.角度的运用：教师设计一些与实际生活相联系的问题，帮助学生初步掌握角度的运用技巧，并提高学生的思维能力。

五、教学评价本教案的主要教学评价标准如下：1.学生对角的定义和度量单位的掌握情况。

2.学生对角的基本性质的能力掌握，特别是对角的大小比较、角的补角和余角、同位角和绝对值等概念理解的情况。

3.学生对角的测量方法和角度的度量掌握情况。

4.学生对角度的运用和角的图像表示的掌握情况。

5.学生在角度问题上的分析和解决问题的能力。

六、教学效果通过教学，学生从学生角的定义和度量单位开始，逐渐理解了角的大小比较、角的补角和余角、同位角和绝对值等概念。

通过互动式教学和比较教学法的运用，学生在角度问题上得到了较好的理解和解决问题的能力。

《角的比较与补角》导学案一、学习目标1、理解角的大小比较的方法。

2、掌握角的和、差运算。

3、理解补角的概念及性质。

二、学习重难点1、重点（1）角的大小比较方法。

（2）角的和、差运算。

（3）补角的性质。

2、难点（1）角的和、差运算中方向的判断。

（2）运用补角的性质解决相关问题。

三、知识回顾1、什么是角？角是由公共端点的两条射线组成的图形。

这个公共端点是角的顶点，这两条射线是角的两条边。

2、角的表示方法有哪些？（1）用三个大写字母表示，如∠AOB，其中 O 是顶点，A、B 分别是角的两条边。

（2）用一个大写字母表示，如∠O，但要注意顶点处只有一个角时才能这样表示。

（3）用数字表示，如∠1。

（4）用希腊字母表示，如∠α。

四、新课导入在日常生活中，我们经常会比较一些东西的大小，比如比较两个线段的长短。

那么对于角，我们又该如何比较它们的大小呢？五、角的比较1、度量法用量角器量出角的度数，然后比较它们的大小。

度数大的角大，度数小的角小。

例如：∠AOB ＝ 50°，∠COD ＝ 30°，因为 50°＞ 30°，所以∠AOB ＞∠COD。

2、叠合法（1）将两个角的顶点及一条边重合。

（2）另一条边在重合边的同侧。

（3）比较另一条边的位置，在重合边同侧，开口大的角大；开口小的角小。

例如：将∠ABC 与∠DEF 进行比较，使∠ABC 的顶点 B 与∠DEF的顶点 E 重合，边 BA 与边 ED 重合，边 BC 和边 EF 都在 ED 的同侧。

如果 BC 落在∠DEF 的内部，那么∠ABC ＜∠DEF；如果 BC 与 EF重合，那么∠ABC ＝∠DEF；如果 BC 落在∠DEF 的外部，那么∠ABC ＞∠DEF。

六、角的和、差1、角的和如图，∠AOC 是∠AOB 与∠BOC 的和，记作：∠AOC ＝∠AOB＋∠BOC。

2、角的差∠AOB 是∠AOC 与∠BOC 的差，记作：∠AOB ＝∠AOC ∠BOC。

1 第八章 第2课时 8.2角的比较 总第2课时设计人： 审查人：【学习目标】：1、 理解两个角的相等、大于、小于关系，会用叠合法比较两个角的大小，会用“＝”、“＞”、“＜”表示两个角的大小关系；2、 了解角的和、差、倍、分，会用图形语言和符号表示角的和差倍分关系；3、 理解角的平分线的概念。

【学习重点】：用叠合法比较两个角的大小，角平分线的概念【学习难点】：会用角的和、差、倍、分关系与角的平分线解决实际问题。

【学习过程】：（教师寄语：态度决定一切！认真决定一切！）一、课前预习：（教师寄语：相信自己！用心探索！用心完成！）认知前提：1，∠1=30° ∠2=60°，∠1与∠2那个大？他们有什么样的等量关系？2，两个线段比较大小的方法是 。

学习任务一： 阅读课本第7页“实验探究”，会用叠合法比较两角的大小并会用符号表示，了解角的和与差，回答下面的问题：1、 任意画两个角∠α和∠β,将∠α和∠β顶点重合，再将∠α的一边与∠β的一边重合，并使两个角的的另一边在重合的边的同侧,问:（1）如果∠β的另一边落在∠α的内部，那∠β ∠α或∠α ∠β（填大于或小于）记做作∠β ∠α或∠α ∠β（填“<”或“>”）（2）如果∠β的另一边落在∠α的外部，那∠β ∠α或∠α ∠β（填大于或小于）记做作∠β ∠α或∠α ∠β（填“<”或“>”）（3）如果两角的顶点和它们的两边都分别重合，那∠α ∠β记做作∠α ∠β2、如图所示，已知三个角的关系，那么∠AOC 与∠AOB 和∠COB 有什么关系？①∠AOB=∠AOC ∠COB②∠AOC=∠AOB ∠COB③∠COB=∠AOB ∠AOC学习任务二：阅读课本第8页，理解角平分线的定义与角的倍、分关系，回答下列问题：如图，已知∠AOC=∠COB ，试写出一下角之间的关系。

①∠AOB=∠AOC ∠COB=____∠AOC②∠AOC=_____∠AOB总结：角平分线定义： 。

青岛版七年级数学下册导学案设计：8.2 角的比较(无答案)8.2角的比较班级姓名学习目标：1、会用叠合法比较两个角的大小，会用“=”、“＜”、“＞”表示两个角的大小关系；2、了解角的和、差、倍、分，会用图形和符号语言表示角的和、差、倍、分关系；3、理解角的平分线的概念。

学习重点：1、用叠合法比较两个角的大小。

2、角平分线的概念。

学习难点：角平分线的应用学习过程一、自主学习1、比较两条线段长短的方法有_________和________。

2、角的度量单位是什么？你会用量角器度量角吗？量出下列各角的度数。

二、合作探究（一）角的比较方法1、度量法：角的度数越大，角就越______。

2、在硬纸板上任意画两个角∠α,∠β然后把他们剪下来,你能比较他们的大小吗?将两个角的顶点重合,再将两角的一边重合,并使两个角的另一边在重合的边的同侧.再比较另一条边的位置⑴∠α落在∠β的外部，∠α ______ ∠β，记作∠α______∠β⑵∠α与∠β重合，∠α ______∠β，记作∠α______∠β．⑶∠α落在∠β的内部，∠α______∠β，记作∠α______∠β归纳总结：叠合法：把一个角放在另一个角上，使_____________，并将______________，使这两个角的另一边_____________________________，就可以明显看出两个角的大小。

（二）角的和、差、倍、分。

“不耻最后”。

即使慢，弛而不息，纵会落后，纵会失败，但一定可以达到他所向的目标。

——鲁迅 第2页1、如图1，如果将∠α与∠β的顶点重合，再将∠α的一边与∠β的一边重合，并使两角的另一边分别在重合边的两侧，这时它们不重合的两边组成∠AOB 。

那么∠AOB 与∠α、∠β有什么关系？这时∠AOB 叫做∠α与∠β的 ，记作： 。

2、如图2，是取两张硬纸片叠合作一起，在其中一张上任意画出一个∠α，然后剪下并分开得到的，它们的大小有什么关系？如上图2，则∠AOB=______+______=2∠___=2∠___。

《角的比较》教案教学目标：知识与技能：理解并掌握利用叠合法比较角的大小，角的和、差、倍分的意义及表示防范，角的平分线的定义及简单应用.过程与方法：通过观察、思考、动手操作，经历和体验角的大小变化，培养识图能力和动手操作能力，渗透类比的数学思想。

.情感、态度与价值观：通过角的大小与线段的大小方法的比较，培养学生知识和方法的迁移能力，通过角的测量活动，体验数形结合的思想，培养学生学习的积极性和主动性。

. 教学重难点：教学重点：1、比较两个角的大小；2、角的平分线及其应用.教学难点：1、角的和与差；2、角的平分线的应用.教学用具：自制的角的模型三对，一副三角尺.教学过程：一、复习导入什么是角？角的概念及表示方法.二、新课研究1、引导学生探究角的比较方法师：（老师拿出两个自制角的模型）请同学们观察，哪个角大？学生：……师：同学们，比较两个角的大小只用眼睛观察是不够的，那么我们使用什么方法比较好呢？我们可以想一想线段是怎样比较大小的.学生1：把两个角重叠放在一起比较，使用叠合法.学生2：用量角器量角的大小，使用度量法.师：两位同学说的都有道理，请同学们想想谁的方法更好呢？更容易操作呢？活动：请同学们在半透明纸上画出一个角、与同伴所画的角比较并得出结论.2、引导学生探究角的运算师：从以上的计算中我们知道：角的度数可以进行运算，事实上，角也可以进行运算。

例如，观察图中的∠AOC、∠COB和∠AOB，这三个角有何关系.ACO B学生1：∠AOC+∠COB=∠AOB学生2：∠AOB-∠AOC=∠COB学生3：∠AOB-∠COB=∠AOC师：同学们回答的很好，我们发现两个角相加或相减得到的和或差也是角.3、引导学生探究角的平分线师：请同学们利用白纸制作一个角，然后把制作的角的两边对折，使角的两边重合，大家会发现有一条折痕，请同学们猜一下，原来的这个角被这条折痕分成两个角，这两个角有什么关系呢？（学生动手制作，并作出猜想，有的可能会回答：相等）师：请同学们想想，我们用什么方法可以比较这两个角的大小呢？学生：度量法师：很好，请同学们自己度量。

课题：8.2角的比较教学目标：1、使学生通过联想线段大小的比较方法，找到角的大小的比较方法。

2、使学生通过联想线段和、差、倍、分的作法，掌握角的和、差、倍、分的作法和计算。

3、使学生掌握角的平分线的定义以及数学表达式。

4、培养学生类比联想的思维能力和对知识的迁移能力。

教学重点：角的两种比较方法、角的和、差、倍、分的作法和计算、角的平分线定义。

教学难点：角平分线定义的各种数学表达式。

教学过程：一、引入课题前面学习了线段的概念之后，紧接着就学习了比较线段的大小以及线段的和、差、倍、分的画法问题。

上节课我们已经学习了角的概念，类似的，今天我们也要学习如何比较角的大小，以及角的和、差、倍、分的画法问题。

二、新授部分（一）角的比较方法：叠合比较法：由线段的叠合比较法知，将要比较的两条线段一端重合，再看另一端的位置。

角的比较也类似，提问谁能用两个三角板演示一下，然后总结，在比较角的大小的过程中，要让角的顶点和角的一条边都重合，看另一条边落在角内还是角外。

（1）记作：∠AOB=∠COD （2）记作：∠AOB＞∠COD （3）记作：∠AOB＜∠COD （二）角平分线角平分线定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

注意：1、角平分线是一条射线，不是一条直线，也不是一条线段。

如图1-32，它是由角的顶点出发的一条射线，因为角的两边都是射线。

2、当一个角有角平分线时，可以产生几个数学表达式。

如图1-32，可写成∵ OC是∠AOB的角平分线，∴∠AOB=2∠AOC=2∠COB，∠AOC=∠COB，∠COB=∠AOC=21∠AOB，练习：如图，∠AOB=60°，OC是∠AOB内部的一条射线，射线OM平分∠AOC，射线ON平分∠COB，求∠MON的度数。

（三）角的和、差、倍、分应用练习1、如图1-33，若∠AOB=∠COB=∠DOC，进行下列填空。

(1)∠AOD=( )+( )+( )；(2)∠AOB=( )∠AOD；(3)∠AOD=( )∠COB；(4)∠DOB=( )=( )+( )。

青岛版数学七年级下册《8.2 角的比较》教学设计2一. 教材分析《8.2 角的比较》这一节内容是青岛版数学七年级下册的重点内容，主要让学生理解并掌握角的概念，学会比较角的大小，并能运用角的概念解决实际问题。

本节内容是在学生已经掌握了直线、射线、线段的基础知识上进行讲授的，为后续学习三角形、四边形等几何图形打下基础。

二. 学情分析学生在学习了直线、射线、线段的基础上，对图形的概念已经有了初步的认识，但角的概念比较抽象，学生理解和接受可能存在一定的困难。

因此，在教学过程中，教师需要借助实物模型、图片等教学辅助工具，帮助学生直观地理解角的概念。

三. 教学目标1.知识与技能目标：让学生理解角的概念，学会比较角的大小，并能运用角的概念解决实际问题。

2.过程与方法目标：通过观察、操作、思考、讨论等活动，培养学生的空间观念和逻辑思维能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生团结协作、积极进取的精神。

四. 教学重难点1.重点：角的概念，比较角的大小。

2.难点：角的大小与边的长短关系的理解，角的分类。

五. 教学方法采用情境教学法、启发式教学法、小组合作学习法等，充分调动学生的积极性，引导学生主动参与教学活动。

六. 教学准备1.教具：直尺、三角板、多媒体课件等。

2.学具：每人一副三角板，一本数学书。

七. 教学过程1.导入（5分钟）教师通过展示一些生活中的图片，如钟表、蝴蝶翅膀、太阳等，引导学生观察这些图片中的角，激发学生的学习兴趣。

同时，教师提问：“你们对角有什么认识？”学生自由发言，教师总结。

2.呈现（10分钟）教师通过多媒体课件，呈现角的概念，讲解角的特点，引导学生直观地理解角的概念。

同时，教师讲解角的大小比较方法，如用直尺比较、用三角板比较等。

3.操练（10分钟）教师分发学具，让学生分组进行角的比较练习，引导学生动手操作，巩固所学知识。

4.巩固（10分钟）教师通过出示一些练习题，让学生独立完成，检验学生对角的概念和比较大小的掌握程度。

C DAB 1OE2新人教版七年级数学上册《角的比较》导学案【学习目标】1、学会比较角的大小，能估计一个角的大小；2、认识角平分线，能画出一个角的角平分线。

3、掌握角的度量和角的单位的换算。

【学习重点】角的大小的比较方法；角平分线 【学习难点】从图形中观察角的和、差关系。

【学习过程】一、预习导学1、比较两条线段的大小关系的方法:2、张开的剪刀两边夹角有无不同？3、比较两个角的方法:4、角平分线:二、探究活动小组探究合作：如图，如何比较两个角∠AOB 和∠CED 的大小？1、 总结方法：（1）（2）2、 合作探究、得出结论角平分线：若OC 是∠AOB 的平分线,则(1)∠AOC=______;(2)∠AOC=12______;(3)∠AOB=2______3、合作学习：P119做一做三、课堂小结1、如何比较两个角的大小2、角平分线的定义及表示四、课堂检测1、若OC 是∠AOB 的平分线,则(1)∠AOC=______; (2)∠ AOC=12______;(3)∠AOB=2_______. 2、如图，直线AB 、CD 相交于O ，∠COE 是直角，∠1=57°，则求∠2的大小。

3、如图,如果∠1=65°15′,∠2=78°30′,求∠3是多少度?312OC AD B4、如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC 、∠AOB 的度数.六、布置作业1、已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC 等于( ) A.120° B.120°或60° C.30° D.30°或90°2、α∠和β∠的顶点和一边都重合,另一边都在公共边的同侧, 且αβ∠>∠,那么α∠的另一半落在β∠的( )A.另一边上B.内部;C.外部D.以上结论都不对3、如图,(1)∠AOC=_____+_____=_____-______;(2)∠AOB=______-______=______-______.4、如图,已知O 是直线AD 上的点,∠AOB,∠BOC,∠COD, 三个角从小到大依次相差25°,求这三个角的度数.5、图所示，OA 丄OB ，OC 丄OD ，OE 为∠BOD 的平分线，∠BOE=18°，求∠AOC 的度数。