25平面的应用举例
- 格式:ppt
- 大小:197.00 KB
- 文档页数:13

线段的长度与坐标公式线段是几何学中的重要概念之一,描述了两个点之间的连续部分。
在数学中,我们经常需要计算线段的长度,而坐标公式则是帮助我们在平面坐标系中计算线段长度的重要工具。
本文将介绍线段的概念,以及如何利用坐标公式计算线段长度。
1. 线段的概念线段是由两个端点所确定的部分,它可以看作是一条有限的直线。
端点是线段的两个极限位置,线段上的点是指处于这两个端点之间的所有点。
线段可以用字母表示,例如AB表示由A点和B点确定的线段。
2. 坐标公式在平面直角坐标系中,我们可以用坐标表示点的位置。
假设A点的坐标为(x1, y1),B点的坐标为(x2, y2),我们可以利用坐标公式求解线段AB的长度。
根据勾股定理,我们知道两点之间的距离可以通过平方差和再开方得到。
因此,线段AB的长度可以计算如下:AB = √[(x2 - x1)² + (y2 - y1)²]3. 例题演示现假设有一条线段,A点的坐标为(1, 2),B点的坐标为(4, 6)。
我们可以利用坐标公式计算线段AB的长度。
首先,我们将A点的坐标(x1, y1)和B点的坐标(x2, y2)代入坐标公式:AB = √[(4 - 1)² + (6 - 2)²]= √[(3)² + (4)²]= √(9 + 16)= √25= 5因此,线段AB的长度为5。
4. 要点总结通过以上例子我们可以总结出计算线段长度的关键步骤:(1) 确定线段的两个端点的坐标。
(2) 将端点的坐标代入坐标公式:AB = √[(x2 - x1)² + (y2 - y1)²](3) 根据公式计算并求解线段的长度。
5. 应用举例线段的长度与坐标公式在实际问题中有着广泛的应用。
例如,在计算机图形学中,我们需要计算图像中两个点之间的距离,以便确定其是否在某个范围内。
此外,线段的长度与坐标公式还可以应用于测量、工程、建模等领域。

平面直角坐标系中的距离计算在平面直角坐标系中,距离计算是一项重要的几何运算。
它被广泛应用于数学、物理、工程和计算机科学等领域。
本文将介绍如何在平面直角坐标系中计算两点之间的距离,以及如何使用这个计算结果解决实际问题。
一、点的坐标表示在平面直角坐标系中,每个点都可以用一对有序数对表示,即(x, y),其中x表示点在x轴上的坐标,y表示点在y轴上的坐标。
例如,点A的坐标为(2, 3),表示它在x轴上的坐标是2,在y轴上的坐标是3。
二、两点之间的距离计算公式在平面直角坐标系中,可以使用勾股定理来计算两点之间的距离。
假设点A的坐标为(x1, y1),点B的坐标为(x2, y2),它们之间的距离d可以通过以下公式计算:d = √((x2 - x1)² + (y2 - y1)²)三、根据距离计算解决实际问题1. 简单应用假设有两个点A(2, 3)和B(5, 7),我们可以使用上述距离计算公式来计算它们之间的距离。
根据公式,我们可以得出:d = √((5 - 2)² + (7 - 3)²)= √(3² + 4²)= √(9 + 16)= √25= 5因此,点A和点B之间的距离为5个单位。
2. 应用举例:直线的长度在工程和建筑领域,我们常常需要计算直线的长度。
假设我们有一条直线AB,其中A点的坐标为(1, 1),B点的坐标为(4, 5)。
为了计算直线AB的长度,我们可以使用距离计算公式:d = √((4 - 1)² + (5 - 1)²)= √(3² + 4²)= √(9 + 16)= √25= 5因此,直线AB的长度为5个单位。
3. 应用举例:点到直线的垂直距离在数学和物理领域,我们经常需要计算一个点到一条直线的垂直距离,比如到直线AB的垂直距离。
为了计算这个距离,我们首先需要求出直线AB的斜率。
假设A点的坐标为(1, 1),B点的坐标为(4, 5),则直线的斜率k可以通过以下公式计算:k = (y2 - y1) / (x2 - x1)= (5 - 1) / (4 - 1)= 4 / 3斜率为4/3。

高中数学:两点之间距离公式引言在数学中,我们经常会遇到计算两点之间的距离的情况。
无论是平面上的两点还是空间中的两点,我们都希望能够准确计算出它们之间的距离。
为了解决这个问题,数学家们发展出了一些距离公式,其中最经典的就是两点之间的距离公式。
本文将重点介绍高中数学中常用的两点之间的距离公式。
平面上两点距离公式我们首先来考虑平面上任意两点之间的距离。
设平面上有两点A和B,其坐标分别为(x₁, y₁)和(x₂, y₂)。
根据勾股定理,我们可以得到平面上两点之间的距离公式如下:d = √((x₂ - x₁)² + (y₂ - y₁)²)其中,d表示两点之间的距离。
这个公式的原理是利用直角三角形的斜边长度公式。
我们将两点之间的水平距离表示为(x₂ - x₁),将垂直距离表示为(y₂ - y₁),然后利用平方和开方的方式,计算出两点之间的距离。
空间中两点距离公式在空间中,我们需要考虑三维坐标系中两点之间的距离。
设空间中有两点A和B,其坐标分别为(x₁, y₁, z₁)和(x₂, y₂, z₂)。
根据勾股定理,我们可以得到空间中两点之间的距离公式如下:d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)这个公式的原理和平面上两点距离公式相同,只是多了一个维度。
应用举例:高中几何问题两点之间的距离公式在解决高中数学几何问题中经常被应用。
例题1已知平面上有三个点A(-2, 1)、B(3, -4)和C(5, 2),求三角形ABC的周长。
根据平面上两点之间的距离公式,我们可以计算出三边的长度:AB = √((-2 - 3)² + (1 - (-4))²) = √(25 + 25) = √50 BC = √((3 - 5)² + (-4 - 2)²) =√((-2)² + (-6)²) = √40 CA = √((-2 - 5)² + (1 - 2)²) = √(49 + 1) = √50所以,三角形ABC的周长为√50 + √40 + √50。
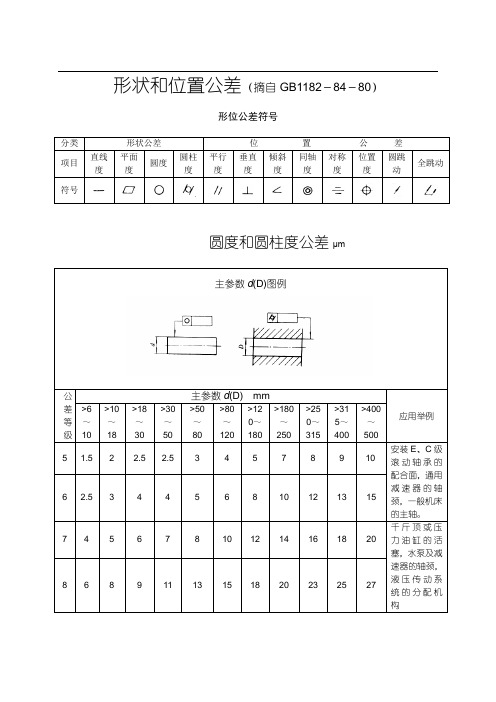
形状和位置公差(摘自GB1182-84-80)形位公差符号分类形状公差位置公差项目直线度平面度圆度圆柱度平行度垂直度倾斜度同轴度对称度位置度圆跳动全跳动符号圆度和圆柱度公差μm主参数d(D)图例公差等级主参数d(D) mm应用举例>6~10>10~18>18~30>30~50>50~80>80~120>120~180>180~250>250~315>315~400>400~5005 1.5 2 2.5 2.5 3 4 5 7 8 9 10安装E、C级滚动轴承的配合面,通用减速器的轴颈,一般机床的主轴。
6 2.5 3 4 4 5 6 8 10 12 13 157 4 5 6 7 8 10 12 14 16 18 20千斤顶或压力油缸的活塞,水泵及减速器的轴颈,液压传动系统的分配机构8 6 8 9 11 13 15 18 20 23 25 279 9 11 13 16 19 22 25 29 32 36 40 起重机、卷扬机用滑动轴承等10 15 18 21 25 30 35 40 46 52 57 63直线度和平面度公差μm主参数L图例公差等级主要参数L mm应用举例≤10>10~16>16~25>25~40>40~63>63~100>100~160>160~250>250~400>400~6305 2 2.5 3 4 56 8 10 12 15 普通精度的机床导轨6 3 4 5 6 8 10 12 15 20 257 5 6 8 10 12 15 20 25 30 40轴承体的支承面,减速器的壳体,轴系支承轴承的接合面8 8 10 12 15 20 25 30 40 50 609 12 15 20 25 30 40 50 60 80 100辅助机构及手动机械的支承面,液压管件和法兰的连接面10 20 25 30 40 50 60 80 100 120 150平行度、垂直度和倾斜度公差μm主参数L、d (D)图例公差等级主参数L、d(D)mm应用举例≤10>10~16>16~25>25~40>40~63>63~100>100~160>160~250>250~400>400~6305 56 8 10 12 15 20 25 30 40垂直度用于发动机的轴和离合器的凸缘,装D、E级轴承和装C、D级轴承之箱体的凸肩6 8 10 12 15 20 25 30 40 50 60平行度用于中等精度钻模的工作面,7~10级精度齿轮传动壳体孔的中心线7 12 15 20 25 30 40 50 60 80 100垂直度用于装F、G级轴承之壳体孔的轴线,按h6与g6连接的锥形轴减速机的机体孔中心线8 20 25 30 40 50 60 80 100 120 150平行度用于重型机械轴承盖的端面、手动传动装置中的传动轴同轴度、对称度、圆跳动和全跳动公差确定μm主参数d(D)、B、L图例公差等级主参数d(D)、B、Lmm应用举例>3~6 >6~10>10~18>18~30>30~50>50~120>120~250>250~5005 3 4 56 8 10 12 156和7级精度齿轮轴的配合面,较高精度的快速轴,较高精度机床的轴套6 5 6 8 10 12 15 20 257 8 10 12 15 20 25 30 408和9级精度齿轮轴的配合面,普通精度高速轴(100r/min以M 12 15 20 25 30 40 50 60 下),长度在1m 以下的主传动轴,起重运输机的鼓轮配合孔和导轮的滚动面表面粗糙度表面粗糙度R粗糙度代号光洁度代号表面形状、特征加工方法应用范围ⅠⅡ除净毛刺铸、锻、冲压、热轧、冷轧用于保持原供应状况的表面微见刀痕粗车,刨,立铣,平铣,钻毛坯粗加工后的表面可见加工痕迹车,镗,刨,钻,平铣,立铣,锉,粗铰,磨,铣齿比较精确的粗加工表面,如车端面、倒角微见加工痕迹车,镗,刨,铣,刮1~2点/cm2,拉,磨,锉滚压,铣齿不重要零件的非结合面,如轴、盖的端面,倒角,齿轮及皮带轮的侧面、平键及键槽的上下面,轴或孔的退刀槽看不见加工痕迹车,镗,刨,铣,铰,拉,磨,滚压,铣齿,刮1~2点/cm2IT12级公差的零件的结合面,如盖板、套筒等与其它零件联接但不形成配合的表面,齿轮的非工作面,键与键槽的工作面,轴与毡圈的摩擦面可辨加工痕迹的方向车,镗,拉,磨,立铣,铰,滚压,刮3~10点/cm2IT8~IT12级公差的零件的结合面,如皮带轮的工作面,普通精度齿轮的齿面,与低精度滚动轴承相配合的箱体孔微辨加工痕迹的方向铰,磨,镗,拉,滚压,刮3~10点/cm2IT6~IT8厅级公差的零件的结合面;与齿轮、蜗轮、套筒等的配合面;与高精度滚动轴承相配合的轴颈;7级精度大小齿轮的工作面;滑动轴承轴瓦的工作面;7~8 级精度蜗杆的齿面不可辨加工痕迹的方向布轮磨,磨,研磨,超级加工IT5、IT6级公差的零件的结合面,与C级精度滚动轴承配合的轴颈;3、4、5级精度齿轮的工作面暗光泽面超级加工仪器导轨表面;要求密封的液压传动的工作面;塞的外表面;活汽缸的内表面注:1. 粗糙度代号I为第一种过渡方式。


平面直角坐标系中的距离公式两点间的距离公式在平面直角坐标系中,我们可以使用距离公式来计算两点之间的距离。
距离公式也被称为欧几里得距离,在数学中被广泛使用。
首先,我们可以计算出两个直角边AC和CB的长度,然后使用毕达哥拉斯定理求得斜边AB的长度,也就是点A和B的距离。
下面就是距离公式的推导过程:对于直角三角形ABC,直角边AC的长度等于点B的x坐标x2减去点A的x坐标x1,即AC=,x2-x1、同样地,直角边CB的长度等于点B的y坐标y2减去点A的y坐标y1,即CB=,y2-y1根据毕达哥拉斯定理,斜边AB的长度等于直角边AC和CB的长度的平方和的平方根,即AB=sqrt(AC²+CB²)。
将AC和CB的长度代入上式,我们可以得到两点之间的距离公式:AB=sqrt((x2-x1)²+(y2-y1)²)上述公式就是平面直角坐标系中两点间的距离公式。
举例来说明距离公式的应用。
假设点A(2,3)和点B(5,7)是平面上的两个点,我们希望计算出这两个点之间的距离。
根据距离公式,我们有AB=sqrt((5-2)²+(7-3)²)=sqrt(3²+4²)=sqrt(9+16)=sq rt(25)=5因此,点A和点B之间的距离为5个单位。
距离公式不仅适用于平面直角坐标系,也适用于三维空间中的点之间的距离计算。
在三维空间中,距离公式的形式类似,只是空间中的点需要用三个坐标来表示。
总结一下,平面上的两点间的距离公式为:AB=sqrt((x2-x1)²+(y2-y1)²)其中,A(x1,y1)和B(x2,y2)是平面上的两个点。
距离公式使用直角三角形的边长关系,根据毕达哥拉斯定理得出两点之间的距离。
距离公式可以帮助我们计算出平面上任意两点之间的距离,对于数学和现实生活中的问题求解都具有重要意义。
授课教师:爱华授课时间:(3)要确定每艘敌舰的位置,两个数据:距离和方位角.么?在学校的哪个方向上?这一方向上还有其他设施吗?怎么区分?(3)要确定京山相对于学校的位置,需要哪些数据?板书设计7.1.1 有序数对教学反思本课容比较简单,但涉及到实际情境,有些学生由于不理解实际情境造成不理解题意,从而出现解题错误.教师授课过程中应当加强学生对情境的理解,从情境中抽象出数学本质的知识,以利于学生解题.授课教师:授课时间:课题7.1.2 平面直角坐标系课时教学目标1.掌握平面直角坐标系的有关概念,会画平面直角坐标系.2通过实际问题抽象出平面直角坐标系及其相关概念,使学生认识平面直角坐标系的原点、横轴和纵轴等,会由坐标描点,由点写出坐标,让学生体会到平面上的点与有序实数对之间的对应关系.3.经历画平面直角坐标系,由点写出坐标和由坐标描点的过程,进一步渗透数形结合的数学思想,培养学生自主探究与合作交流的学习习惯.教学重点正确认识平面直角坐标系,会准确地由点写出坐标,由坐标描点.教学难点各象限及各坐标轴上点的坐标的特点,平面上的点与有序实数对之间的对应关系.教学方法探究法、演示法、练习法教学手段多媒体教学手段课型新授课教学环节教学容教师活动学生活动授课教师:授课时间:课题7.2.1 用坐标表示地理位置课时教学目1.掌握用坐标表示地理位置的方法.2.通过学生观察、探索用坐标表示地理位置的方法,发展学生数形结合的意识.3.通过用坐标表示地理位置的方法,让学生体验数学活动充满着探索与创造.学生体会了解。
图7-2-8播放央视新闻联播关于2014月3日市鲁甸县发生6.5级地震的新闻片段.新闻报道中是用什么方法表示地震位置授课教师:授课时间:。