初二平面几何习题集及规范标准答案

第一题、如图，F为。

0外一点，PA、PB分别切6于A、B, PCD为ST割线，CO 交CX）于另一点E, AC、EB交于点F,证明：CD平分匕ADF。

"证明方法一：如图，延长ED交CA于K,根据条件知四边形CADB为调和四边形，故ED、EC、EA、EB构成一组调和线束，进而知K、C、A、F构成一组调和点列。

而KD±CD, 故CD平分ZADFo 3证明方法二：如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半，且PA = PB,故点P为TkABF的外心。

于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。

又PA= PF,故CD 平分Z A DF。

3第二题、如图，AB为©0直径，C、D为O。

上两点，且在AB同侧，。

在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明：E、C、页、D四点共圆。

“证明：如图，延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。

又在圆内接六边形CCADDB中使用帕斯卡定理，知K、E、F三点共线，从而KM丄卽于価。

于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。

K第三题、如图，AB为。

直径，C、D为伽上两点'且在AB同侧，O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。

于点G,证明；ZCEF = 2/AGF。

“证明：如图，根据条件知匕CF D =典牌=(脸-®；(i对-命)=Z CAB + / DBA = ZECF + ZEDF；且EC = ED；故点E 为△CED 外心。

于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。

所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo，2 2第四題、如图，AB为直径，P为AB延长线上一点，PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点，AF交于K,求证：AP为ZXPCK外扬圆的切线。

初二上期几何习题集含答案1、如图：在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线，DE⊥AB垂足为E，DF⊥AC，垂足为点F，且BD=CD 求证：BE＝CF3、如图，点B和点C分别为∠MAN两边上的点，AB=AC。

（1）按下列语句画出图形：①AD⊥BC，垂足为D；②∠BCN的平分线CE与AD的延长线交于点E；③连结BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：____≌____，____≌____；（3）并选择其中的一对全等三角形予以证明。

已知：AB=AC，AD⊥BC，CE平分∠BCN，求证：△ADB≌△ADC；△BDE≌△CDE。

AB D CM NE4、如图，PB、PC分别是△ABC的外角平分线且相交于点P.求证：点P在∠A的平分线上AB C5、如图，△ABC中，p是角平分线AD，BE的交点. 求证：点p在∠C的平分线上6、下列说法中，错误的是（）A．三角形任意两个角的平分线的交点在三角形的内部B．三角形两个角的平分线的交点到三边的距离相等C．三角形两个角的平分线的交点在第三个角的平分线上D．三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图，AP、CP分别是△ABC外角∠MAC与∠NCA的平分线，它们相交于点P，PD⊥BM于点D，PF⊥BN于点F．求证：BP为∠MBN的平分线。

9、如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．求证：点C在∠AOB 的平分线上．10、如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.（1）若连接AM，则AM是否平分∠BAD？请你证明你的结论；（2）线段DM与AM有怎样的位置关系？请说明理由．11、八（1）班同学上数学活动课，利用角尺平分一个角（如图所示）．设计了如下方案：（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由；PM⊥OA，PN⊥OB．此方案是否可行？请说明理由．ADEBFC求证：（1）PE=PF；（2）点P在∠BAC的角平分线上。

八年级下数学几何题（有答案）八年级下期末复习5如图1，四边形ABCD为正方形，E在CD上，∠DAE的平分线交CD于F，BG⊥AF于G，交AE于H．（1）如图1，∠DEA=60°，求证：AH=DF；（2）如图2，E是线段CD上（不与C、D重合）任一点，请问：AH与DF有何数量关系并证明你的结论；（3）如图3，E是线段DC延长线上一点，若F是△ADE中与∠DAE相邻的外角平分线与CD的交点，其它条件不变，请判断AH与DF的数量关系（画图，直接写出结论，不需证明）．证明：（1）延长BG交AD于点S∵AF是HAS的角的平分线，BS⊥AF∴∠HAG=∠SAG，∠HGA=SGA=90°又∵AG=AG∴△AGH≌△AGS∴AH=AS，∵AB∥CD∴∠AFD=∠BAG，∵∠BAG+∠ABS=∠ABS+∠ASB=90°∴∠BAG=∠ASB∴∠ASB=∠AFD又∵∠BAS=∠D=90°，AB=AD∴△ABS≌△DAF∴DF=AS∴DF=AH．（2）DF=AH．同理可证DF=AH．（3）DF=AH如图，在△ABC中，点O是AC边上的一个动点（点O不与A、C 两点重合），过点O作直线MN ∥BC，直线MN与∠BCA的平分线相交于点E，与∠DCA（△ABC的外角）的平分线相交于点F．（1）OE 与OF相等吗？为什么？（2）探究：当点O运动到何处时，四边形AECF是矩形？并证明你的结论．（3）在（2）中，当∠ACB等于多少时，四边形AECF为正方形．（不要求说理由）解：（1）如图所示：作EG⊥BC，EJ⊥AC，FK⊥AC，F H⊥BF，因为直线EC，CF分别平分∠ACB与∠ACD，所以EG=EJ，FK=FH，在△EJO与△FKO中，∠AOE=∠CON ∠EJO=∠FKO EJ=FK ，所以△EJO≌△FKO，即OE=OF（2）当OA=OC，OE=OF时，四边形AECF是矩形，证明：∵OA=OC，OE=OF，∴四边形AECF为平行四边形，又∵直线MN与∠BCA的平分线相交于点E，与∠DCA（△ABC的外角）的平分线相交于点F．∴∠ACE=∠BCE，∠ACF=∠FCD，由∠BCE+∠ACE+∠ACF+∠FCD=180°，∴∠ECA+∠ACF=90°，即∠ECF=90°，∴四边形AECF为矩形；（3）由（2）可知，四边形AECF是矩形，要使其为正方形，再加上对角线垂直即可，即∠ACB=90°（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？即：FG=（AB+BC+AC）（直接写出结果即可）（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是解如图（1）FG=1 /2 （AB+BC+AC）；（2）答：FG=1 /2 （AB+AC-BC）；证明：延长AG交BC于N，延长AF交BC于M∵AF⊥BD，A G⊥CE，∴∠AGC=∠CGN=90°，∠AFB=∠BFM=90°在Rt△AGC和Rt△CGN中∠AGC=∠CGN=90°，CG=CG，∠ACG=∠NCG∴Rt△AGC≌Rt△CGN∴AC=CN，AG=NG同理可证：AF=FM，AB=BM．∴GF是△AMN的中位线∴GF=1/ 2 MN．∵AB+AC=MB+CN=BN+MN+CM+MN，BC=BN+MN+CM ∴AB+AC-BC=MN∴GF=1 /2 MN=1 /2 （AB+AC-BC）；（3）线段FG与△ABC三边之间数量关系是：GF=1/ 2 （AC+BC-AB）．已知：△ABC中，以AC、BC为边分别向形外作等边三角形ACD 和BCE，M为CD中点，N为CE 中点，P为AB中点．（1）如图1，当∠ACB=120°时，∠MPN的度数为；（2）如图2，当∠ACB=α（0°＜α＜180°）时，∠MPN的度数是否变化？给出你的证明．解：（1）∠MPN的度数为60°；（2）∠MPN的度数不变，仍是60°，理由如下：证明：取AC、BC的中点分别为F，G，连接MF、FP、PG、GN，∵MF是等边三角形ACD的中位线，∴MF=1 /2 AD=1 /2 AC，MF∥AD，∵PG是△ABC的中位线，∴PG=1/ 2 AC，PG∥AC，∴MF=PG，同理：FP=CG，∴四边形CFPG是平行四边形，∴∠CFP=∠CGP，∴∠MFC+∠CFP=∠CGN+∠CGP，即∠MFP=∠PGN，∴△MFP≌△PGN（SAS），∴∠FMP=∠GPN，∵PG∥AC，∴∠1=∠2，在△MFP中，∠MFC+∠CFP+∠FMP+∠FPM=180°，又∵∠MFC=60°，∴∠CFP+∠FMP+∠FPM=120°，∵∠CFP=∠1+∠3，∴∠1+∠3+∠FMP+∠FPM=120°，∵∠1=∠2，∠FMP=∠GPN，∴∠2+∠3+∠GPN+∠FPM=120°，又∵∠3+∠FPM+∠MPN+∠GPN+∠2=180°，∴∠MPN=60°．如图，在平面直角坐标系中，A是反比例函数y=k/x（x＞0）图象上一点，作AB⊥x轴于B点，AC⊥y轴于C点，得正方形OBAC的面积为16．（1）求A点的坐标及反比例函数的解析式；．（2）点P（m，16/3 ）是第一象限内双曲线上一点，请问：是否存在一条过P点的直线l与y轴正半轴交于D点，使得BD⊥PC？若存在，请求出直线l的解析式；若不存在，请说明理由；（3）连BC，将直线BC沿x轴平移，交y轴正半轴于D，交x轴正半轴于E点（如图所示），DQ⊥y轴交双曲线于Q点，QF⊥x轴于F点，交DE于H，M是EH的中点，连接QM、OM．下列结论：①QM+OM的值不变；②QM/OM的值不变．可以证明，其中有且只有一个是正确的，请你作出正确的选择并求值．解：（1）∵正方形OBAC的面积为16，∴A（4，4）；（2分）将A点代入反比例函数y=k /x （x＞0）中，得反比例函数的解析式：y=16/ x ；（2）将y=16/ 3 代入y=16 /x 得：P(3，16 /3 )；设存在点D，延长PC交x轴于E点；∵∠COE=∠DOB=90°，∠ECO=∠DCP，∴∠CEO=∠ODB；而OC=OB，∴△COE≌△BOD，∴OE=OD；而C（0，4），P(3，16 /3 )，∴直线CP的解析式为y=4 /9 x+4；当y=0时，x=-9，∴E（-9，0），故D（0，9），∴直线l的解析式为：y=-11/ 9 x+9（3）选②，值为1．连FM，∵DE∥BC，∴OE=OD=QF，而M是Rt△FHE的斜边中点，∴EM=HM=FM；∵∠OEH=∠QFM=45°，∴△QMF≌△OME；∴QM=OM；∴QM OM =1．。

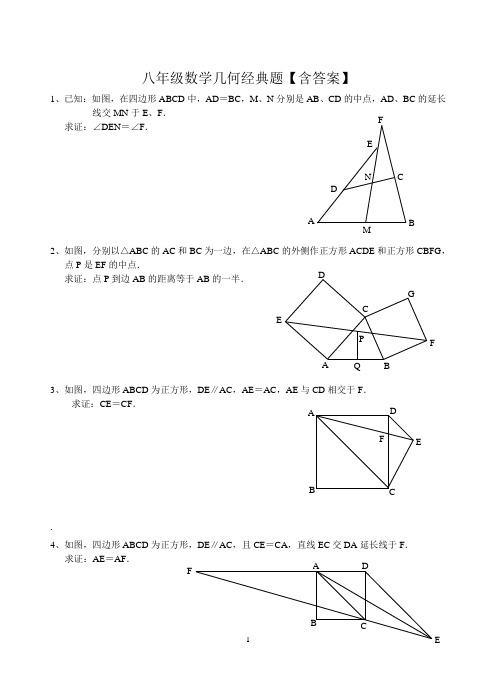
F八年级数学几何经典题【含答案】1、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．2、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．3、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．.4、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．B5、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF平分∠DCE ．求证：PA ＝PF ．6、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE ＝CF ．求证：∠DPA ＝∠DPC ．7如图，△ABC 中，∠C 为直角，∠A=30°，分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ，DE 与AB 交于F 。

求证：EF=FD 。

8如图，正方形ABCD 中，E 、F 分别为AB 、BC 的中点，EC 和DF 相交于G ，连接AG ，求证：AG=AD 。

9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA，九年级数学【答案】1.如下图连接AC 并取其中点Q ，连接QN 和QM ，所以可得∠QMF=∠F ，∠QNM=∠DEN 和∠QMN=∠QNM ，从而得出∠DEN ＝∠F 。

2.过E,C,F 点分别作AB 所在直线的高EG ，CI ，FH 。

可得PQ=2EG FH+。

由△EGA ≌△AIC ，可得EG=AI ，由△BFH ≌△CBI ，可得FH=BI 。

千里之行，始于足下。

初二平面几何知识点讲解及习题平面几何是几何学的一个分支，在平面几何中，我们研究的是在一个平面上的图形和其相关的性质。

初二阶段的平面几何主要包括直线与角度的性质、三角形的性质以及圆的相关知识。

下面我将就这些知识点进行详细讲解，并提供一些相应的习题。

一、直线与角度的性质1. 平行线与垂直线：平行线是指在同一个平面内，永远不会相交的两条直线。

而垂直线是指与另一条直线相交时，所成的角度为90度。

习题：1）在下面的平面图中，判断哪些线段是平行线。

参考答案：AB和CD是平行线。

2）在下面的平面图中，判断哪些线段是垂直线。

参考答案：线段AB和线段CD是垂直线。

2. 角的性质：角是由两条射线共同端点组成的图形。

常见的角有直角（90度）、锐角（小于90度）和钝角（大于90度）。

习题：1）下面的平面图中，判断哪些角是直角，哪些角是锐角，哪些角是钝角。

第1页/共3页锲而不舍，金石可镂。

参考答案：角A是直角，角B是锐角，角C是钝角。

二、三角形的性质1. 三角形的内角和：三角形的内角和等于180度。

习题：1）求下面三角形中缺失的角。

参考答案：角A=60度，角B=60度。

2. 三角形的分类：三角形可以根据边长和角度的大小进行分类。

根据边长，三角形可以分为等边三角形（三边相等）、等腰三角形（两边相等）和普通三角形（边长都不相等）。

根据角度，三角形可以分为直角三角形（有一个角为直角）、锐角三角形（三个角都为锐角）和钝角三角形（有一个角为钝角）。

习题：1）在下面的平面图中，判断三角形的类型。

参考答案：三角形ABC是等边三角形，三角形DEF是等腰三角形，三角形GHI是直角三角形。

三、圆的相关知识1. 圆的性质：圆是由一条曲线上各点到圆心的距离都相等的图形。

圆上的任意一条弧所对的圆心角都相等，而圆心角的度数等于所对的弧所夹的角度的一半。

千里之行，始于足下。

习题：1）在下面的平面图中，判断哪些是圆，哪些是弧。

参考答案：图中的(a)和(b)是圆，(c)和(d)是弧。

初二平面几何考试题及答案一、选择题（每题2分，共20分）1. 下列哪个图形是轴对称图形？A. 正方形B. 圆C. 长方形D. 等边三角形答案：B2. 一个圆的半径为5cm，那么它的周长是多少？A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案：C3. 一个三角形的内角和是多少度？A. 90°B. 180°C. 360°D. 540°答案：B4. 一个平行四边形的对角线互相平分，那么这个平行四边形是：A. 矩形B. 菱形C. 梯形D. 不规则四边形答案：A5. 如果一个角是直角的补角，那么这个角的度数是多少？A. 45°B. 90°C. 135°D. 180°答案：A6. 一个正六边形的内角是多少度？A. 60°B. 90°C. 120°D. 180°答案：C7. 一个圆的面积公式是：A. πr²B. πdC. π(r+d)²D. πr²/48. 一个三角形的外角等于与它相邻的内角的：A. 补角B. 余角C. 相等D. 两倍答案：A9. 一个矩形的对角线相等，那么这个矩形是：A. 正方形B. 长方形C. 梯形D. 不规则四边形答案：A10. 一个圆的内接四边形的对角线互相垂直，那么这个四边形是：A. 矩形B. 菱形C. 梯形D. 平行四边形答案：B二、填空题（每题2分，共20分）11. 一个直角三角形的两条直角边分别为3cm和4cm，那么它的斜边长是________cm。

答案：512. 一个正五边形的每个内角是________度。

答案：10813. 如果一个三角形的三边长分别为a, b, c，且满足a² + b² = c²，那么这个三角形是________三角形。

答案：直角14. 一个圆的半径增加1cm，那么它的面积增加了________πcm²。

几何作图（导学案）知识过关1. 说出日常生活现象中应用的数学原理：（1）如图1，计划把河水引到水池A 中，先作AB ⊥CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是__________________________________________．图1 图2（2）如图2，PC ∥AB ，QC ∥AB ，则点P ，C ，Q 在一条直线上，理由是_______________________________________．2. 估计下列角的度数，然后用量角器度量并填在横线上：（结果精确到1°）∠BOC =____，∠DOE =____，∠MON =_____，∠POQ =____．1. 常见几何语言书写：①连接AB ；②延长线段AB 到点C ，使BC =AB ； ③延长线段AB 交线段CD 的延长线于点E ； ④过点A 作AB ∥CD ； ⑤过点A 作AB ⊥CD 于点E ． 2. 几何作图：①理解题意，找准_____________； ②___________________；③位置不确定时，需考虑_______________．➢ 精讲精练1. 如图，已知四点A ，B ，C ，D ，按要求作图： （1）连接AB ，CD ；（2）延长CD 交AB 的延长线于点G ； （3）过点B 作直线BM ⊥CD ，垂足为点M ．Q CP AB QOOOPNMEDCB2. 如图，点M ，P 分别在直线AB 上和直线AB 外，以下是在此图基础上作图的过程及作法，请根据作图的过程叙述作法．ACB D3. 作一条线段等于已知线段．已知：如图，线段a ． 求作：线段AB ，使AB =a ． 作法：（1）作射线AP ；（2）以_________为圆心，_______为半径作弧，交射 线AP 于点B ．___________即为所求．4. 已知线段a ，b （），作一条线段，使它等于a +b ．作法：（1）作射线AP ；（2）在射线AP 上依次截取__________，_________． ___________即为所求．5. 如图，已知线段AB ，请用尺规按下列要求作图： （1）延长线段AB 到点C ，使BC =AB ； （2）延长线段BA 到点D ，使AD =AC ．a b ba BA6.在直线l上任取一点A，截取AB=8 cm，再截取AC=12 cm，则线段BC的长为______________．7.在直线l上任取一点A，截取AB=16 cm，再截取AC=40 cm，则点B与AC的中点D之间的距离为__________．8.已知A，B，C三点在同一条直线上，AB=60，BC=40，M，N分别为线段AB，BC的中点，则MN的长为__________．9.已知线段AB=16 cm，点C在直线AB上，AC=3BC，则BC的长为______________．10.从O点出发的三条射线OA，OB，OC，若∠AOB是直角，∠AOC为30°，则∠BOC的度数为_____________．11.已知∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，则∠MON的度数为_____________．12.已知∠AOB=40°，∠AOD=3∠AOB，OC平分∠AOB，OM平分∠AOD，则∠MOC的度数为_____________．13.已知∠AOB=48°，∠BOC=3∠AOC，OM平分∠AOC，ON平分∠AOB，则∠MON的度数为__________．【参考答案】➢知识过关1.（1）垂线段最短；（2）过直线外一点，有且只有一条直线与已知直线平行．2.30°，60°，110°，140°2.①关键词；②设计作图方案，作出草图；③分类讨论．➢精讲精练1.略2.（1）连接（2）PH⊥AB于点H（3）PQ∥AB3.作图略（2）点A，线段a长（3）线段AB4.作图略（2）AB=a，BC=b，线段AC5.略6.4cm或20cm7.4cm或36cm8.50或109.4cm或8cm10.60°或120°11.30°或60°12.40°或80°13.18°或36°几何作图（当堂过关）1.如图，已知点P在∠AOB的内部，过点P作PC∥OB，交OA于点C，过点P作PD⊥OA于点D．2.已知线段a，b，画一条线段，使它等于2a-b．（保留作图痕迹）ab3.已知∠AOB=80°，∠BOC=60°，OM平分∠AOB，ON平分∠BOC，则∠MON的度数为_____________，并作图说明．①作草图：②设计方案：【参考答案】1. 略2. 略3. 70°或10°，作图说明略几何作图（习题）➢ 例题示范例1：在直线l 上任取一点A ，截取AB =20cm ，再截取BC=50cm ，则AB 的中点D 与AC 的中点E 之间的距离为__________，并作图说明． 思路分析首先，理解题意，找关键词，其中l 为直线，AB ，BC 为l 上的两条线段． 其次，设计作图方案，作图．作直线l ，任取一点作为A ，取适当长作为AB ；此时点B 位置固定，但点C 可在点B 左侧或右侧，位置不定，故分两种情况． ①点C 在点B 左侧，如图，接着取AB 的中点D ，AC 的中点E ．设计算法： ②点C 在点B 右侧，如图，接着取AB 的中点D ，AC 的中点E ．设计算法：2050l2050l 11221225AB AC DE AD AE BC =+==+=2050l2050l综上，DE 的长度为25cm ．➢ 巩固练习1. 如图1，点C ，D 是直线AB 外两点，按下列要求作图： （1）____________________________________________； （2）____________________________________________． 得到的图形如图2，请在横线填上作法．2. 如图，已知线段AB ，按要求作图：①分别以点A 和点B 为圆心、以AB 的长为半径作弧，两弧相交于点C 和点D ；②作直线CD ，交线段AB 于点E ；③请通过测量猜想线段AB 和直线CD 的位置关系，线段AE 与线段BE 的数量关系．3. 作图：已知线段a ，b （），作一条线段，使它等于．（保留作图痕迹，不必写作法）4. 已知线段AB =15cm ，点C 在直线AB 上，且BC =2AB ，则线段AC 的长为________________，并作图说明．11221225AC AB DE AE AD BC =-==-=ABCD 图1图2A Ba b >a b -ba5. 已知点C 在直线AB 上，若AC =4cm ，BC =6cm ，E ，F 分别为线段AC ，BC 的中点，则EF 的长为_____________，并作图说明．6. 已知线段AB=24，点C 在直线AB 上，BC=3AC ，M ，N 分别为线段AB ，AC 的中点，则MN 的长为_____________，并作图说明．7. 已知从点O 出发的三条射线OA ，OB ，OC ，若∠AOB =60°，，则∠BOC 的度数为________________，并作图说明．8. 已知∠AOB 为直角，∠BOC =40°，OM 平分∠AOB ，ON 平分∠BOC ，则∠MON 的度数为_______________，并作图说明．9. 已知∠AOB =120°，∠AOC =4∠BOC ，OD 平分∠AOB ，OE 平分∠AOC ，则∠EOD 的度数为____________，并作图说明．【参考答案】 ➢ 巩固练习1. （1）作射线DC 交AB 于点E（2）过点C 作CF ⊥DE 于点C ，交AB 于点F 2. 作图略，AB ⊥CD ，AE =BE 3. 作图略13AOC AOB ∠∠O BA4.15cm或45cm，作图说明略5.1cm或5cm，作图说明略6.9或18，作图说明略7.40°或80°，作图说明略8.25°或65°，作图说明略9.12°或20°，作图说明略。

F八年级数学几何经典题【含答案】1、已知：如图，在四边形ABCD 中，AD ＝BC ，的中点，AD 、BC 的延长线交MN 于E 、F ． 求证：∠DEN ＝∠F ．2、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点． 求证：点P 到边AB 的距离等于ABB3、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．.4、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．5、设P 是正方形ABCD 一边BC 上的任一点，PF求证：PA ＝PF ．E6、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且AE ＝CF ．求证：∠DPA ＝∠DPC ．7如图，△ABC 中，∠C 为直角，∠A=30°，分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ，DE 与AB 交于F 。

求证：EF=FD 。

8如图，正方形ABCD 中，E 、F 分别为AB 、BC 的中点，EC 和DF 相交于G ，连接AG ，求证：AG=AD 。

FPDE CBA9、已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF，九年级数学【答案】1.如下图连接AC 并取其中点Q ，连接QN 和QM ，所以可得∠QMF=∠F ，∠QNM=∠DEN 和∠QMN=∠QNM ，从而得出∠DEN ＝∠F 。

2.过E,C,F 点分别作AB 所在直线的高EG ，CI ，FH 。

可得PQ=2EGFH。

由△EGA ≌△AIC ，可得EG=AI ，由△BFH ≌△CBI ，可得FH=BI 。

从而可得PQ=2AI BI=2AB，从而得证。

精心整理习题1如图，P为等边△ABC内一点，∠APB=113°，∠APC=123°，试说明：以AP、BP、CP为边长可以构成一个三角形，并确定所构成三角形的各内角的度数．BC 的边长是多少？把△APC绕点A顺时针旋转60°到△AMB，则AM=AP=2，BM=PC=4,∠PAM=60°连结PM，则△PAM是等边三角形，∴PM=2∴△ACD≌△BDE∴AC=BE=BC+CD习题5 如图,己知在△ABC中,AB=AC,∠BAC=90°,点D是BC上的任意一点,探究BD2+CD2与AD2的关系习题6 D,E是等腰直角三角形斜边BC所在直线上的两点，满足∠DAE=135°，求证CD2+BE2=DE2∵∠BAC=90°，AC=AB，∴将△ABE绕点A逆时针转90°，得△ACF，所以MB=MC=ME=MD角EMD=角MCD*2; 角EMB=角BCE*2所以角DMB=角EMD+角EMB=2*(角MCD+角MCB)=2*角C=90°所以BM=DM且BM垂直DM(2)证明:取AE的中点G,AC的中点F,连接DG,MG,BF,MF.又M为CE中点,则:MF=AE/2=DG;GM=AC/2=BF;GM∥AC;MF∥AE.(中位线的性质)得:∠MFC=∠EAC=∠EGM;又∠BFC=∠EGD=90度.则∠MFB=∠DGM. ∴?⊿BFM≌⊿MGD(SAS),BM=DM;∠FBM=∠GMD.又GM平行AC,BF垂直AC,则GM垂直BF.故∠FBM+∠BMG=90度=∠GMD+∠BMG,即∠BMD=90度,得:BM⊥DM.明显的对称。

如果P点距离AB与距离CD距离不一样大会是最小吗？显然不会，因为如果不一样明显可以在中线另一侧找到一个对应点拥有同样的距离。

因此P点一定在BC中垂线上，而Q的横坐标一定与P一致，原因不解释，很明显。

以A为原点，AD为x轴，BA为y轴建立坐标系，则P横坐标为500。

平面几何练习题及答案一、选择题1. 已知三角形ABC中，∠A=90°，AB=3cm，BC=4cm，求AC的长度。

A. 5cmB. 6cmC. 7cmD. √7cm2. 在矩形PQRS中，若PS=6cm，QR=8cm，求对角线PR的长度。

A. 10cmB. 12cmC. 14cmD. √(6²+8²)cm3. 圆O的半径为5cm，点A在圆上，点B在圆外，且OA=5cm，OB=10cm，求AB的长度。

A. 5cmB. 10cmC. 15cmD. √(10²-5²)cm二、填空题4. 已知等腰三角形的底边长为6cm，两腰长为5cm，求其面积。

答案：____cm²5. 已知直角三角形的两条直角边分别为3cm和4cm，求其外接圆的半径。

答案：____cm6. 已知正六边形的边长为a，求其内切圆的半径。

答案：____三、计算题7. 在三角形DEF中，DE=7cm，DF=8cm，EF=9cm，求三角形DEF的面积。

8. 已知圆的半径为r，圆心为O，点A在圆上，点B在圆外，OA=r，OB=2r，求AB的长度。

9. 已知矩形LMNP的长为10cm，宽为6cm，求其内切圆的半径。

四、证明题10. 证明：在直角三角形中，斜边的中线等于斜边的一半。

11. 证明：如果一个三角形的两边和其中一边上的高相等，那么这个三角形是等腰三角形。

12. 证明：在等边三角形中，每个内角都是60°。

五、解答题13. 已知圆的半径为r，求圆的周长和面积。

14. 已知矩形ABCD的长为a，宽为b，求对角线AC的长度。

15. 已知三角形ABC的三个顶点坐标分别为A(x1, y1)，B(x2, y2)，C(x3, y3)，求三角形ABC的面积。

答案：1. D2. D3. D4. 12cm²5. 2.5cm6. a/√37. 27cm²8. 5r9. 2cm10. 利用直角三角形斜边上的中线等于斜边的一半的性质证明。