安徽安庆五校联盟2015届高三下学期3月联考数学文试题word版含答案

2015年皖北协作区高三年级联考参考答案数学（文科）一、选择题1A、2B、3D、4C、5A、6C、7D、8C、9A、10D、二、填空题11、 25； 12、 9； 13、8 ； 14、,2()2()-∞-∞，＋； 15、①③④⑤ 三、解答题16．解：(1)由正弦定理，得3sin cos B C ＝()sin 13cos C B -化简可得 sin 3sin()C B C =+又A ＋B ＋C ＝π，所以sin C ＝3sin A ，因此sin sin A C ＝13. --------------------------6分 (2)由sin sin A C ＝13得c ＝3a . 由余弦定理及cos B ＝16得 b 2＝a 2＋c 2－2ac cos B ＝a 2＋9a 2－6a 2×16＝9a 2. 所以b ＝3a .又a ＋b ＋c ＝14.从而a ＝2，因此b ＝6. -----------------------------12分17.解：(1)因为“综合素质”科目中成绩等级为B 的考生有10人， 所以该考场有10400.25=人 所以该考场考生中“综合素质”科目中成绩等级为A 的人数为400.0753⨯= --------------4分（2）“综合素质”科目成绩为D 的频率为10.0750.2500.3750.2000.1----=所以该考场考生“综合素质”科目的平均分为900.075800.250700.375600.1500.26960⨯+⨯+⨯+⨯+⨯=>所以“综合素质”的考核合格 -----------------8分（3）该考场考生中“服务技能”科目中成绩等级为A 的人数为40(10.3750.3750.1500.025)3⨯----=所以两科考试中，共有6人得分等级为A ，又恰有两人的两科成绩等级均为A ，所以还有2人只有一个科目得分为A ，设这四人为甲，乙，丙，丁，其中甲，乙是两科成绩都是A 的同学，则在至少一科成绩等级为A 的考生中，随机抽取两人进行访谈，基本事件空间为{Ω={甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁}},有6个基本事件设“随机抽取两人进行访谈，这两人的两科成绩等级均为A ”为事件B ，所以事件B 中包含的基本事件有1个，则1()6p B =. -----------------12分18．（1）证明：如图，取AE 中点M ，连接BM 、FM ． F 是DE 中点，FM ∴是ADE ∆的中位线，//FM AD ∴，且12FM AD =， 又//BC AD ，且12BC AD =，//FM BC ∴且FM BC =， ∴四边形FMBC 是平行四边形，//FC MB ∴．FC ⊄面,ABE MB ⊂面ABE ，//FC ∴平面ABE ． -----------------6分（2）取DH 中点N ，连接FN 、EH ，F 是DE 的中点，1//,=2FN EH FN EH ∴且． ABC ∆是等腰直角三角形，AC BC =，M 是AB 的中点， EH AB ∴⊥ 又平面ABCD ⊥平面ABE ，平面ABCD 平面ABE AB =，EH ⊂平面ABCDEH ABCD ∴⊥平面 FN ABCD ∴⊥平面=S 111(12)21222DCH ADH BCH S S S ∆∆∆--=⨯+⨯⨯-⨯=梯形ABCD 又12FN EH ==111332F DCH DCH V S FN -∆∴==⨯=-----------------12分 或 由F 是ED 的中点且HC HD ⊥，得1112122F DCH E DCH V V HC HD HE --=== -----------------12分 19．解： 11(),31n n n n a a f a a +==+（） DAFC E HBM N1131113,113,n n n n n n a a a a a a +++∴==+∴-=∴数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项，3为公差的等差数列. -----------------6分1(2)113(1)32,1,32n n n n a a n =+-=-∴=-由（）得 -----------------7分111111,323133231n n a a n n n n +⎛⎫⋅=⋅=⋅- ⎪-+-+⎝⎭ 111111134473231n S n n ⎛⎫∴=-+-+⋅⋅⋅+- ⎪-+⎝⎭ 11=(1)33131n n n -=++ -----------------13分20．解：（1）原函数的定义域为()∞+，02'1)(xa x a x f -+=由题意3,1212)2(2'=∴=-+=a a a f -----------------5分 ()'212()ln 1()a g x a x x x a a g x x x x-=---=+- 2221(1)(1)x ax a x x a x x -++---+-== '()011g x x x a ===-由得，或-----------------7分'112()011()00112()1,1,0,1(1,)11,2()0011,12()0,1(1,);1,110,1,()0,1,a a g x x a g x x x a a g x a a a a g x a a g x a a a a g x ->>><<-<<<>->--+∞-==+∞<-<<<-+∞--≤≤若即时，由得由得或所以时，的增区间为（）减区间为（）,若即时，的减区间为（，）若即时，可得的减区间为（）,增区间为（）若即时的增区间为（）减1+∞区间为（，）综上所述：2,()1101,a g x a a >--∞+若时的增区间为（，）,减区间为（，1）,（） 2()0a g x =+∞若时，的减区间为（，）2()0,1(1,);1,1a g x a a <<-+∞-若1时，可得的减区间为（）,增区间为（） 1()0,1,(1,)a g x ≤+∞若时，的增区间为（）减区间为 ----------------------13分21．法一：解：（1） 由题意可知m>n>0, 22,.a m b n == 2112c c a =⎧⎪⎨=⎪⎩ 213,1,.24c a b ==∴= 13422=+∴y x 椭圆的方程为 -----------------4分 （2）设0000(,),(0,0),(0,)P x y x y Q t >>，则10220=+n y m x ， 12(,0),(,0)F c F c -1001(,),(,)F P x c y FQ c t ∴=+= 12,F P F Q O ⋅=000y t ∴+=(x +c)c ①2,,P F Q 三点共线00y t x c c∴=-- ② 由①②得0000()0cy c x c y x c-++⋅=- 22200x y c m n -==-即 -----------------------------------9分 220011m n x y m n+=+= 000011x n y nx y =-⎧⎨=⎩∴+=联立可解得 1P x y ∴+=点在定直线上 -------------------------------13分法二：解：（1） 由题意可知m>n>0,因为椭圆焦距为1，所以12=-n m ，43,1,2121==∴=-n m m n m ，所以离心率为 13422=+∴y x 椭圆的方程为 -----------------4分 （2）设)(0,0y x p 为第一象限内椭圆上的点，则10220=+ny m x ， )0,(22n m F F -∴为椭圆的右焦点，211001(()(PF y x Q F m F P x y FQ m ∴=∴-∴==的方程为120,00PF PF O x m n x ⋅=+-+=∴+=因为所以 22000m n x y --+=即 -----------------------------------9分 2211m n x y m n +=+=000011x ny n x y =-⎧⎨=⎩∴+=联立可解得1P x y ∴+=点在定直线上 -------------------------------13分。

安徽省安庆市2015届高考数学三模试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设i是虚数单位，若复数z1=3+2i，z2=4﹣mi（m∈R），且z1•z2为实数，则m的值为（）A．6 B．﹣6 C．D．﹣2．（5分）抛物线y=ax2（a＜0）的准线方程是（）A．y=﹣B．y=﹣C．y=D．y=3．（5分）函数f（x）=x2+cosx的图象大致是（）A．B．C．D．4．（5分）设{a n}是等比数列，则对任何n∈N*，都有=（）A．B．C．D．5．（5分）阅读程序框图，若输入m=4，n=6，则输出a，i分别是（）A．a=12，i=3 B．a=12，i=4 C．a=8，i=3 D．a=8，i=46．（5分）有四个游戏盘，将它们水平放稳后，在上面扔一颗玻璃小球，若小球落在阴影部分，则可中奖，小明要想增加中奖机会，应选择的游戏盘是（）A．B．C．D．7．（5分）x，y满足约束条件若z=x+ky的最小值为﹣2，则z的最大值为（）A．12 B．16 C．20 D．248．（5分）在空间四边形ABCD中，AB=AD，CB=CD．E，F，G，H分别是AB，BC，CD，DA的中点，则下列命题中正确的是（）A．E，F，G，H四点不共面B．EFGH是梯形C．EG⊥FH D．EFGH是矩形9．（5分）“a≤0”是“函数f（x）=|（ax﹣1）x|在区间（0，+∞）内单调递增”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件10．（5分）若定义域为D的函数f（x）满足：①f（x）在D内是单调函数；②存在[a，b]⊆D，使得f（x）在[a，b]上的值域为[，]，则称函数f（x）为“半值函数”．已知函h（x）=log c（c x+t）（c＞0，c≠1）是“半值函数”则实数t的取值范围为（）A．（0，+∞）B．（﹣∞，）C．（，+∞）D．（0，）二、填空题：本大题共5小题，每小题5分，共25分.11．（5分）如图是不锈钢保温饭盒的三视图，根据图中数据（单位：cm），求得该饭盒的表面积为cm2．12．（5分）调查某电脑公司的三名产品推销员，其工作年限与年推销金额数据如表：由表中数据算出线性回归方程=bx+a中的b=，若该电脑公司第四名推销员的工作年限为6年，则估计他的年推销金额为万元．推销员编号 1 2 3工作年限x（年） 3 5 10年推销金额y（万元） 2 3 413．（5分）已知△ABC的内角为A，B，C，2sinA=sinB=3sinC，则cosB的值是．14．（5分）已知函数f（x）的导函数为f′（x），且满足f（x）=3x2+2xf′（2），则f′（5）=．15．（5分）在△ABC中，=+k，=k+，其中k∈R，且|=1，||=2，与的夹角为120°对于以下结论：①|+|=；②若点D是边BC的中点，则=（+）；③若∠A为直角，则k=；④若∠A为钝角，则k＜且k≠﹣1或k＞；⑤若∠A为锐角，则＜k＜．其中所有正确命题的序号是（把你认为正确命题的序号都填上）．三、解答题：本大题共6小题，共75分.解答应写文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域.16．（12分）已知函数f（x）=2sin（x+）•cos（x+）﹣sin（2x+3π）．（1）求f（x）的最小正周期；（2）若将f（x）的图象向左平移个单位，得到函数g（x）的图象，求函数g（x）在区间上的最大值和最小值．17．（12分）某中学一位2015届高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如下表所示：积极参加班级工作不积极参加班级工作合计学习积极性高18 7 25学习积极性不高 6 19 25合计24 26 50（Ⅰ）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？（Ⅱ）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取两名学生参加某项活动，问两名学生中有1名男生的概率是多少？（Ⅲ）学生的积极性与对待班级工作的态度是否有关系？请说明理由．附：K2=p（K2≥k0）0.10 0.05 0.025 0.010 0.005 0.001k0 2.706 3.841 5.024 6.635 7.879 10.82818．（12分）如图，在空间几何体ABCDEF中，底面CDEF为矩形，DE=1，CD=2，AD⊥底面CDEF，AD=1，平面BEF⊥底面CDEF，且BE=BF=．（Ⅰ）证明：AB∥平面CDEF；（Ⅱ）求几何体A﹣DBC的体积V．19．（13分）设函数f（x）=lnx+ax2+bx（a，b∈R），其图象在点（1，f（1））处的切线平行于x轴．（Ⅰ）若a=1，求函数f（x）的极值；（Ⅱ）试讨论函数f（x）的单调性．20．（13分）已知数列{a n}的首项a1=1，a n+1=，n∈N+．（Ⅰ）证明：数列{}是等比数列；（Ⅱ）求数列{}的前n项和S n．21．（13分）设F1（﹣c，0），F2（c，0）分别是椭圆E：+=1（a＞b＞0）的左、右焦点．（Ⅰ）若点P（，2）在椭圆E上，且c=，求椭圆E的方程；（Ⅱ）已知椭圆E的离心率为，若过点F1（﹣c，0）的直线交椭圆E于A，B两点，且|AF1|=3|F1B|．证明：AB⊥AF2．安徽省安庆市2015届高考数学三模试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设i是虚数单位，若复数z1=3+2i，z2=4﹣mi（m∈R），且z1•z2为实数，则m的值为（）A．6 B．﹣6 C．D．﹣考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：直接利用复数的乘法运算法则化简，通过复数的概念求出m即可．解答：解：复数z1=3+2i，z2=4﹣mi（m∈R），z1•z2=12+2m+（8﹣3m）i．z1•z2为实数，由8﹣3m=0得，．故选：C．点评：本题考查复数的代数形式的混合运算，复数的基本概念的应用，基本知识的考查．2．（5分）抛物线y=ax2（a＜0）的准线方程是（）A．y=﹣B．y=﹣C．y=D．y=考点：抛物线的标准方程．专题：计算题；圆锥曲线的定义、性质与方程．分析：抛物线y=ax2（a＜0）化为标准方程，即可求出抛物线的准线方程．解答：解：抛物线y=ax2（a＜0）可化为，准线方程为．故选B．点评：本题考查抛物线的性质，考查学生的计算能力，抛物线方程化为标准方程是关键．3．（5分）函数f（x）=x2+cosx的图象大致是（）A．B．C．D．考点：函数的图象．专题：函数的性质及应用．分析：利用函数的奇偶性排除选项，然后利用特殊值判断即可．解答：解：易知函数是偶函数，故排除A，C．又f（0）=cos0=1，故排除B，故选：D．点评：本题考查函数的图象的判断，函数的奇偶性以及函数值的应用，考查分析问题解决问题的能力．4．（5分）设{a n}是等比数列，则对任何n∈N*，都有=（）A．B．C．D．考点：等比数列的性质．专题：等差数列与等比数列．分析：由等比数列的性质，可得a1a n+1=a2a n=…=a n+1a1，再由累乘法即可得到所求．解答：解：因为a1a n+1=a2a n=…=a n+1a1，所以，即，故=．故选B．点评：本题主要考查等比数列的性质、累乘求积法．属于中档题．5．（5分）阅读程序框图，若输入m=4，n=6，则输出a，i分别是（）A．a=12，i=3 B．a=12，i=4 C．a=8，i=3 D．a=8，i=4考点：程序框图．专题：阅读型；图表型；算法和程序框图．分析：由程序框图依次计算第一、第二、第三次运行的结果，直到满足条件满足a被6整除，结束运行，输出此时a、i的值．解答：解：由程序框图得：第一次运行i=1，a=4；第二次运行i=2，a=8；第三次运行i=3，a=12；满足a被6整除，结束运行，输出a=12，i=3．故选A．点评：本题考查了直到型循环结构的程序框图，解答的关键是读懂程序框图．6．（5分）有四个游戏盘，将它们水平放稳后，在上面扔一颗玻璃小球，若小球落在阴影部分，则可中奖，小明要想增加中奖机会，应选择的游戏盘是（）A．B．C．D．考点：几何概型．专题：概率与统计．分析：根据几何概型的概率公式，要使中奖率增加，则对应的面积最大即可．解答：解：要使中奖率增加，则对应的面积最大即可，则根据几何概型的概率公式可得，A．概率P=，B．概率P=，C概率P=，D．概率P=，则概率最大的为，故选：A．点评：本题主要考查几何概型的概率计算，比较基础．7．（5分）x，y满足约束条件若z=x+ky的最小值为﹣2，则z的最大值为（）A．12 B．16 C．20 D．24考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用数形结合即可求出k的值．解答：解：显然k＞0．联立解得，．过点时，直线在y轴上的截距最小，即最小，所以，解得k=4．过点C（4，4）时，z=x+4y取最大值20．故选：C点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合是解决本题的关键．8．（5分）在空间四边形ABCD中，AB=AD，CB=CD．E，F，G，H分别是AB，BC，CD，DA的中点，则下列命题中正确的是（）A．E，F，G，H四点不共面B．EFGH是梯形C．EG⊥FH D．EFGH是矩形考点：平面的基本性质及推论．专题：空间位置关系与距离．分析：根据中位线的性质判断EFGH是平行四边形，根据等腰三角形的性质判断垂直关系即可得到结论．解答：解：∵E，F，G，H分别是AB，BC，CD，DA的中点，∴FG∥BD，EF∥BD，且FG=BD，EF=/BD，即EF∥FG，EF=FG，即EFGH是平行四边形．取BD的中点P，则AP⊥BD，CP⊥BD，∴BD⊥面APC，BD⊥AC．即EFGH是矩形．故选：D．点评：本题考查空间中直线与干线之间的位置关系，解题的关键是掌握空间中直线与直线之间位置关系的判断方法，本题涉及到线线平行的证明，中位线的性质等要注意这些知识在应用时的转化方式．9．（5分）“a≤0”是“函数f（x）=|（ax﹣1）x|在区间（0，+∞）内单调递增”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：函数的性质及应用；简易逻辑．分析：对a分类讨论，利用二次函数的图象与单调性、充要条件即可判断出．解答：解：当a=0时，f（x）=|x|，在区间（0，+∞）内单调递增．当a＜0时，，结合二次函数图象可知函数f（x）=|（ax﹣1）x|在区间（0，+∞）内单调递增．若a＞0，则函数f（x）=|（ax﹣1）x|，其图象如图它在区间（0，+∞）内有增有减，从而若函数f（x）=|（ax﹣1）x|在区间（0，+∞）内单调递增则a≤0．∴a≤0是”函数f（x）=|（ax﹣1）x|在区间（0，+∞）内单调递增”的充要条件．故选：C．点评：本题考查了二次函数的图象与单调性、充要条件，考查了数形结合的思想方法，考查了推理能力与计算能力，属于中档题．10．（5分）若定义域为D的函数f（x）满足：①f（x）在D内是单调函数；②存在[a，b]⊆D，使得f（x）在[a，b]上的值域为[，]，则称函数f（x）为“半值函数”．已知函h（x）=log c（c x+t）（c＞0，c≠1）是“半值函数”则实数t的取值范围为（）A．（0，+∞）B．（﹣∞，）C．（，+∞）D．（0，）考点：对数函数的图像与性质；函数单调性的性质．专题：函数的性质及应用．分析：根据指数函数和对数函数的图象和性质以及复合函数的单调性可知h（x）都是R上的增函数，再根据“半值函数”的定义得到log c（c x+t）=，构造关于m的方程，根据根与系数的关系，即可得到结论．解答：解：∵h（x）=log c（c x+t）（c＞0，c≠1），c＞1或0＜c＜1，h（x）都是R上的增函数，∴，即log c（c x+t）=，即c x+t=有两不等实根，令c x=m（m＞0）∴t=m﹣m2有两不等正根，∴解得0＜t＜．故选：D．点评：本题考查了新定义，以及对数函数指数函数的图象和性质，复合函数的单调性，方程根的问题，属于中档题．二、填空题：本大题共5小题，每小题5分，共25分.11．（5分）如图是不锈钢保温饭盒的三视图，根据图中数据（单位：cm），求得该饭盒的表面积为900πcm2．考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：由已知中的三视图可得，该几何体是一个圆柱与半球球的组合体，计算圆柱的底面面积，侧面积，半球的曲面面积，相加可得答案．解答：解：由已知中的三视图可得，该几何体是一个圆柱与半球球的组合体，圆柱的底面半径（球半径）为r=10cm．圆柱的高为h=30cm，故组合体的表面积S=2πrh+3πr2=900πcm2，故答案为：900π．点评：本题考查了由三视图求几何体的表面积和体积，根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键．12．（5分）调查某电脑公司的三名产品推销员，其工作年限与年推销金额数据如表：由表中数据算出线性回归方程=bx+a中的b=，若该电脑公司第四名推销员的工作年限为6年，则估计他的年推销金额为3万元．推销员编号 1 2 3工作年限x（年） 3 5 10年推销金额y（万元） 2 3 4考点：线性回归方程．专题：概率与统计．分析：根据所给的两组数据，做出x和y的平均数，写出这组数据的样本中心点，根据线性回归方程一定过样本中心点，得到线性回归直线一定过的点的坐标．最后根据第4名推销员的工作年限为6年，即当x=6时，把自变量的值代入线性回归方程，得到y的预报值，即估计出第4名推销员的年推销金额．解答：解：由条件可知，，代入回归方程，可得a=，所以=，当x=6 时，，估计他的年推销金额为3万元．故答案为：3．点评：本题考查线性回归方程的意义，线性回归方程一定过样本中心点，本题解题的关键是正确求出样本中心点，题目的运算量比较小，是一个基础题．13．（5分）已知△ABC的内角为A，B，C，2sinA=sinB=3sinC，则cosB的值是．考点：正弦定理．专题：解三角形．分析：由已知等式求出sinA，sinB，sinC的比值，利用正弦定理求出a，b，c的比值，设出a，b，c，利用余弦定理表示出cosB，代入计算即可求出值．解答：解：∵2sinA=sinB=3sinC，∴sinA：sinB：sinC=3：2：2，利用正弦定理化简得：a：b：c=3：2：2，设a=3k，b=2k，c=2k，∴cosB===．故答案为：点评：此题考查了正弦、余弦定理，以及比例的性质，熟练掌握定理是解本题的关键．14．（5分）已知函数f（x）的导函数为f′（x），且满足f（x）=3x2+2xf′（2），则f′（5）=6．考点：导数的运算．专题：计算题．分析：将f′（2）看出常数利用导数的运算法则求出f′（x），令x=2求出f′（2）代入f′（x），令x=5求出f′（5）．解答：解：f′（x）=6x+2f′（2）令x=2得f′（2）=﹣12∴f′（x）=6x﹣24∴f′（5）=30﹣24=6故答案为：6点评：本题考查导数的运算法则、考查通过赋值求出导函数值．15．（5分）在△ABC中，=+k，=k+，其中k∈R，且|=1，||=2，与的夹角为120°对于以下结论：①|+|=；②若点D是边BC的中点，则=（+）；③若∠A为直角，则k=；④若∠A为钝角，则k＜且k≠﹣1或k＞；⑤若∠A为锐角，则＜k＜．其中所有正确命题的序号是①②③④⑤（把你认为正确命题的序号都填上）．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由条件利用两个向量的加减法及其几何意义，两个向量的数量积的定义和公式，一元二次不等式的解法，逐一判断各个选项是否正确，从而得出结论．解答：解：由题意可得，|=1，||=2，=1×2×cos120°=﹣1，∴|+|====，故①正确．若点D是边BC的中点，由=+k，=k+，可得==（+），故②正确．若∠A为直角，则=（+k）•（k+）=k（+）+（k2+1）=﹣k2+5k﹣1=0，求得k=，故③正确．若∠A为钝角，则=（+k）•（k+）=k（+）+（k2+1）=﹣k2+5k﹣1＜0，求得k＜或k＞，故④正确．若∠A为锐角，则=（+k）•（k+）=k（+）+（k2+1）=﹣k2+5k﹣1＞0，求得k＜，故⑤正确．故答案为：①②③④⑤．点评：本题主要考查平面向量的数量积、夹角、运算法则，一元二次不等式的解法，体现了转化的数学思想，属于中档题．三、解答题：本大题共6小题，共75分.解答应写文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域.16．（12分）已知函数f（x）=2sin（x+）•cos（x+）﹣sin（2x+3π）．（1）求f（x）的最小正周期；（2）若将f（x）的图象向左平移个单位，得到函数g（x）的图象，求函数g（x）在区间上的最大值和最小值．考点：函数y=Asin（ωx+φ）的图象变换；三角函数的周期性及其求法．专题：三角函数的图像与性质．分析：（1）利用倍角公式及诱导公式化简，然后由周期公式求周期；（2）由三角函数的图象平移得到函数g（x）的解析式，结合x的范围求得函数g（x）在区间上的最大值和最小值．解答：解：（1）====2sin（2x+）．∴f（x）的最小正周期为；（2）由已知得=，∵x∈，∴，故当，即时，；当，即x=0时，．点评：本题考查了三角恒等变换及其应用，考查了三角函数的图象和性质，考查了三角函数的最值，是基础题．17．（12分）某中学一位2015届高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如下表所示：积极参加班级工作不积极参加班级工作合计学习积极性高18 7 25学习积极性不高 6 19 25合计24 26 50（Ⅰ）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？（Ⅱ）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取两名学生参加某项活动，问两名学生中有1名男生的概率是多少？（Ⅲ）学生的积极性与对待班级工作的态度是否有关系？请说明理由．附：K2=p（K2≥k0）0.10 0.05 0.025 0.010 0.005 0.001k0 2.706 3.841 5.024 6.635 7.879 10.828考点：独立性检验的应用．专题：应用题；概率与统计．分析：（Ⅰ）随机调查这个班的一名学生，有50种情况，抽到不积极参加班级工作且学习积极性不高的学生，有19种情况，即可求出概率；（Ⅱ）利用列举法确定基本事件的个数，即可求出两名学生中有1名男生的概率是多少？（Ⅲ）求出K2，与临界值比较，即可得出结论．解答：解：（Ⅰ）随机调查这个班的一名学生，有50种情况，抽到不积极参加班级工作且学习积极性不高的学生，有19种情况，故概率是…（2分）（Ⅱ）设这7名学生为a，b，c，d，e，A，B（大写为男生），则从中抽取两名学生的所有情况是：ab，ac，ad，ae，aA，aB，bc，bd，be，bA，Bb，cd，ce，cA，cB，de，dA，dB，eA，eB，AB共21种情况，其中含一名男生的有10种情况，∴．…（8分）（Ⅲ）根据∴我们有99.9%把握认为“学生的学习积极性与对待班级工作的态度”有关系．…（12分）点评：本题考查独立性检验的应用和等可能事件的概率，本题解题的关键是正确利用观测值公式求出观测值，正确理解临界值对应的概率的意义．18．（12分）如图，在空间几何体ABCDEF中，底面CDEF为矩形，DE=1，CD=2，AD⊥底面CDEF，AD=1，平面BEF⊥底面CDEF，且BE=BF=．（Ⅰ）证明：AB∥平面CDEF；（Ⅱ）求几何体A﹣DBC的体积V．考点：棱柱、棱锥、棱台的体积；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（Ⅰ）过点B作BM⊥EF，利用平面与平面垂直的性质，可得BM⊥底面CDEF，利用AD⊥底面CDEF，可得BM∥AD，从而可证明四边形ADMB为平行四边形，即可证明AB∥平面CDEF；（Ⅱ）利用等体积转化，即可求几何体A﹣DBC的体积V．解答：（Ⅰ）证明：过点B作BM⊥EF，∵平面BEF⊥底面CDEF，且BE=BF=，∴M为等腰直角三角形底边EF的中点，∴BM⊥底面CDEF，∵AD⊥底面CDEF，∴BM∥AD，又∵AD=BM=1，∴四边形ADMB为平行四边形，∴AB∥DM，∵AB⊄底面CDEF，DM⊂底面CDEF，∴AB∥平面CDEF…（6分）（Ⅱ）解：∵（d为三棱锥B﹣ADC高）∵DE⊥DC，DE⊥AD，∴DE⊥平面ADC又∵平面BEF⊥底面CDEF，DE⊥EF，∴DE⊥平面BEF∴平面BEF∥平面ADC，∵d=ED=1，，∴V A﹣BCD==…（12分）点评：本题考查平面与平面垂直的性质，考查线面平行的判定，考查三棱锥体积的计算，考查学生分析解决问题的能力，属于中档题．19．（13分）设函数f（x）=lnx+ax2+bx（a，b∈R），其图象在点（1，f（1））处的切线平行于x轴．（Ⅰ）若a=1，求函数f（x）的极值；（Ⅱ）试讨论函数f（x）的单调性．考点：利用导数研究函数的单调性；利用导数研究函数的极值．专题：导数的综合应用．分析：（Ⅰ）先求出函数f（x）的导数，将a=1代入，求出f′（x）=0的根，从而求出函数的单调性，求出函数的极值；（Ⅱ）先求出函数g（x）的导数，通过讨论a的范围，从而求出的单调性．解答：解：（Ⅰ）f（x）=lnx+ax2+bx 的定义域为（0，+∞），f′（x）=2ax++b，∵图象在点（1，f（1））处的切线平行于x轴，∴f′（1）=2a+b+1=0，b=﹣2a﹣1，f′（x）=2ax+﹣2a﹣1=，当a=1时，．当时，f′（x）＞0，f（x）单调增；时，f′（x）＜0，f（x）单调减；x＞1时，f′（x）＞0，f（x）单调增．∴f（x）的极大值为，f（x）的极小值为f（1）=﹣2．（Ⅱ）由（Ⅰ）知：．∴a≤0时，x∈（0，1）f′（x）＞0，f（x）单调增，x∈（1，+∞）f′（x）＜0，f（x）单调减；时，x∈（0，1）f′（x）＞0，f（x）单调增，f′（x）＜0，f（x）单调减，f′（x）＞0，f（x）单调增；时，x∈（0，+∞）f′（x）＞0，f（x）单调增；时，f′（x）＞0，f（x）单调增，f′（x）＜0，f（x）单调减，x∈（1，+∞）f′（x）＞0，f（x）单调增．点评：本题考查了函数的单调性，考察导数的应用，考查分类讨论思想，是一道中档题．20．（13分）已知数列{a n}的首项a1=1，a n+1=，n∈N+．（Ⅰ）证明：数列{}是等比数列；（Ⅱ）求数列{}的前n项和S n．考点：数列的求和；等比关系的确定．专题：等差数列与等比数列．分析：（Ⅰ）由题意化简递推公式后，代入化简后，利用等比数列的定义即可证明结论；（Ⅱ）由（Ⅰ）和等比数列的通项公式求出a n，利用错位相减法、分组求和法、等差、等比数列的前n项和公式，求出数列的前n项和S n．解答：证明：（Ⅰ）由题意得，a n+1=，则=（1+），∴=（），又a1=1，则，∴数列{}是以为首项、为公比的等比数列，∴a n=2+（n﹣1）×=（n+3），∴=，则，，两式相减得，==，∴S n=；（Ⅱ）由（I）得，=，则，∴=，令，①，②，①﹣②得，==，则，所以S n=T n+1+2+3+…+n=+=．点评：本题考查了等比数列的定义、通项公式，等差、等比数列的前n项和公式，以及错位相减法、分组求和法求数列的和，属于中档题．21．（13分）设F1（﹣c，0），F2（c，0）分别是椭圆E：+=1（a＞b＞0）的左、右焦点．（Ⅰ）若点P（，2）在椭圆E上，且c=，求椭圆E的方程；（Ⅱ）已知椭圆E的离心率为，若过点F1（﹣c，0）的直线交椭圆E于A，B两点，且|AF1|=3|F1B|．证明：AB⊥AF2．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线中的最值与范围问题．分析：（Ⅰ）因为F1，，且点在椭圆E上，列式求得椭圆方程．（Ⅱ）在△AF1F2中和在△ABF2中，分别利用余弦定理求得，再根据条件列出等式求解．解答：解：（Ⅰ）因为F 1，，且点在椭圆E 上，所以．因此b2=a2﹣c2=9﹣3=6．故椭圆E的方程为．…（5分）（Ⅱ）因为，所以．设|F1B|=t（t＞0），则|AF1|=3t，|AB|=4t．在△AF1F2中，，在△ABF2中，…（10分）所以=，整理得，3at=a2，a=3t．于是|AF2|=3t=|AF1|，|BF2|=5t，|AB|=4t，∠A=90°，故AB⊥AF2．…（13分）点评：本题主要考查求椭圆方程的方法和利用余弦定理解决综合问题得能力，属于中档题，再2015届高考中时常涉及．。

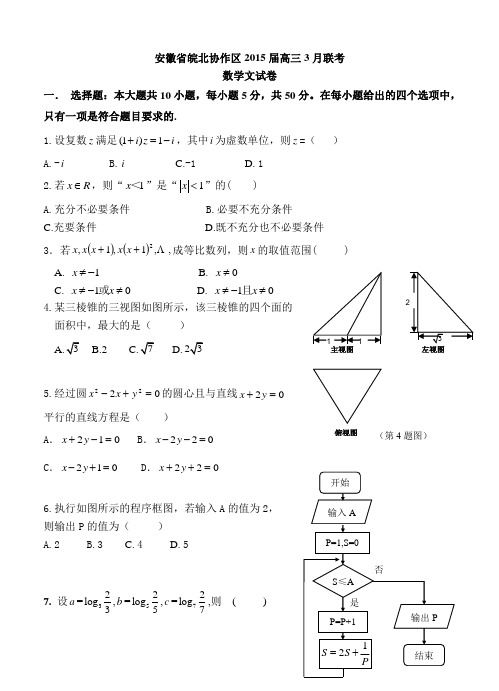
左视图俯视图 （第4题图）安徽省皖北协作区2015届高三3月联考数学文试卷一． 选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的.1.设复数z 满足(1)1i z i +=-，其中i 为虚数单位，则z =（ ） A.-i B.i C.-1 D. 12.若x R ∈，则“1x ＜”是“1x <”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3．若)()(,,1,1,2++x x x x x 成等比数列，则x 的取值范围( )A. 1x ≠-B. 0x ≠C. 10x x ≠-≠或D. 10x x ≠-≠且4.某三棱锥的三视图如图所示，该三棱锥的四个面的 面积中，最大的是（） B.2 C. D.5.经过圆0222=+-y x x 的圆心且与直线02=+y x 平行的直线方程是（ ）A ．012=-+y xB ．220x y --=C ．210x y -+=D ．022=++y x6.执行如图所示的程序框图，若输入A 的值为2， 则输出P 的值为（ ） A.2 B.3 C. 4 D. 57. 设a =32log 3,b =52log 5,c =72log 7,则 ( )A. c b a >>B. b c a >>C. a c b >>D. a b c >>8.函数321x x y =-的图像大致是（ ）9. 定义在R 上的函数的图像关于直线23=x 对称，且对任意的实数x 都有3()()2f x f x =-+，(1)1,f -=(0)2f =-，则(2013)(2014)(2015)f f f ++= ( )A ．0B ．－2C ．1D ．210. 已知, a b 是单位向量，a b ⋅ =0.若向量 c 满足2,c a b -+=则 c 的最大值为（ ）1 B.2 1 2二．填空题：本大题共5小题，每小题5分，共25分。

2014-2015学年安徽省安庆市五校联盟高三（下）3月月考数学试卷（文科） 一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知集合A={1，2，}，集合B={y|y=x2，x∈A}，则A∩B=（ ） A． {} B． {2} C． {1} D． ? 2．已知i是虚数单位，若（2﹣i）?z=i3，则z=（ ） A． B． C． D． 3．下列函数中，在区间（0，+∞）上为增函数的是（ ） A． y=ln（x﹣1） B． y=|x﹣1| C． D． y=sinx+2x 4．抛物线的焦点坐标是（ ） A．（0，﹣1） B．（0，1） C．（1，0） D．（﹣1，0） 5．将函数y=sinx的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是（ ） A． y=sin（2x﹣） B． y=sin（2x﹣） C． y=sin（x﹣） D． y=sin（x﹣） 6．已知A，B，C为△ABC的三个内角，命题p：A=B；命题q：sinA=sinB．则￢p是￢q的（ ） A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 7．若直线x+y=a+1被圆（x﹣2）2+（y﹣2）2=4所截得的弦长为2，则a=（ ） A． 1或5 B．﹣1或5 C． 1或﹣5 D．﹣1或﹣5 8．已知向量=（3，﹣4），=（6，﹣3），=（2m，m+1）．若，则实数m的值为（ ） A． B．﹣3 C． D．﹣ 9．对任意实数a，b定义运算“?”：，设f（x）=（x2﹣1）?（4+x），若函数y=f（x）+k 的图象与x轴恰有三个不同交点，则k的取值范围是（ ） A．（﹣2，1） B． [0，1] C． [﹣2，0） D． [﹣2，1） 10．P为椭圆+=1上任意一点，EF为圆N：（x﹣1）2+y2=4的任意一条直径，则?的取值范围是（ ） A． [0，15] B． [5，15] C． [5，21] D．（5，21） 二.填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡的相应位置. 11．已知直线l1：ax+2y+6=0，l2：x+（a﹣1）y+a2﹣1=0，若l1⊥l2，则a=． 12．已知a＞0，b＞0，且点（a，b）在直线x+y=2上，则2a+2b的最小值为 ． 13．设m＞1，在约束条件下，目标函数z=x+my的最大值等于2，则m=． 14．已知sinθ﹣cosθ=，θ∈（0，π），则tanθ=． 15．若函数f（x）=x3+a|x﹣1|在[0，+∞）上单调递增，则实数a的取值范围是 ． 三.解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内. 16．（12分）（2015春?安庆月考）设向量=（sin2x，sin），=（cos，﹣cos2x），f（x）=?． （1）求f（x）的最小正周期； （2）求f（x）在区间[0，π]上的单调递减区间． 17．（12分）（2015春?安庆月考）公差d＞0的等差数列{an}中，a1=2，a1、a2、a4成等比数列； （1）求数列{an}的通项公式； （2）数列{bn}满足an=+++…+，求数列{bn}的通项公式． 18．（12分）（2014春?芜湖期末）△ABC中内角A、B、C的对边分别为a、b、c，且2acosC=2b ﹣c． （Ⅰ）求角A的大小； （Ⅱ）如果a=1，求b+c的取值范围． 19．（13分）（2015春?哈尔滨校级期中）已知函数f（x）=lnx﹣ax，其中a＞0． （1）当a=1时，求f（x）在[1，e]上的最大值； （2）若1≤x≤e时，函数f（x）的最大值为﹣4，求函数f（x）的表达式． 20．（13分）（2015春?安庆月考）已知数列{an}的前n项和为Sn，a1=1，an+1=2Sn+1（n∈N*）． （1）求数列{an}的通项公式； （2）求数列{}的前n项和Tn． 21．（13分）（2012?长春模拟）如图，椭圆经过点（0，1），离心率． （l）求椭圆C的方程； （2）设直线x=my+1与椭圆C交于A，B两点，点A关于x轴的对称点为A′（A′与B不重合），则直线A′B与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由． 2014-2015学年安徽省安庆市五校联盟高三（下）3月月考数学试卷（文科） 参考答案与试题解析 一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知集合A={1，2，}，集合B={y|y=x2，x∈A}，则A∩B=（ ） A． {} B． {2} C． {1} D． ? 考点：交集及其运算． 专题：集合． 分析：将A中的元素代入集合B中的等式中求出y的值，确定出B，求出A与B的交集即可． 解答：解：当x=1时，y=1；当x=2时，y=4；当x=时，y=， ∴B={1，4，}， ∴A∩B={1}． 故选：C． 点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2．已知i是虚数单位，若（2﹣i）?z=i3，则z=（ ） A． B． C． D． 考点：复数代数形式的乘除运算． 专题：计算题． 分析：利用复数的运算法则和共轭复数的意义，即可得出． 解答：解：∵（2﹣i）?z=i3，∴（2+i）（2﹣i）z=﹣i（2+i），5z=﹣2i+1， ∴z=， 故选：A． 点评：本题考查了复数的运算法则和共轭复数的意义，属于基础题． 3．下列函数中，在区间（0，+∞）上为增函数的是（ ） A． y=ln（x﹣1） B． y=|x﹣1| C． D． y=sinx+2x 考点：函数单调性的判断与证明． 专题：函数的性质及应用． 分析：结合对数函数，指数函数，三角函数的图象及性质，分别对各个选项进行判断，从而得出答案． 解答：解：对于A：定义域是（1，+∞），∴y=ln（x﹣1）在（1，+∞）递增， 对于B：y=|x﹣1|在（0，1）递减，在（1，+∞）递增， 对于C：y=在（0，+∞）递减， 对于D：y'=cosx+2＞0，所以y=sinx+2x在区间（0，+∞）上为增函数， 故选：D． 点评：本题考查了函数的单调性问题，考查了对数函数，指数函数，三角函数的性质，是一道基础题． 4．抛物线的焦点坐标是（ ） A．（0，﹣1） B．（0，1） C．（1，0） D．（﹣1，0） 考点：抛物线的简单性质． 专题：计算题． 分析：把抛物线的方程化为标准方程，求出 p值和开口方向，从而写出焦点坐标． 解答：解：抛物线的标准方程为 x2=﹣4y，开口向下， p=2，=1，故焦点为（0，﹣1）， 故选 A． 点评：本题考查抛物线的标准方程，以及简单性质的应用． 5．将函数y=sinx的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是（ ） A． y=sin（2x﹣） B． y=sin（2x﹣） C． y=sin（x﹣） D． y=sin（x﹣） 考点：函数y=Asin（ωx+φ）的图象变换． 专题：分析法． 分析：先根据左加右减进行左右平移，然后根据横坐标伸长到原来的2倍时w变为原来的倍进行横向变换． 解答：解：将函数y=sinx的图象上所有的点向右平行移动个单位长度，所得函数图象的解析式为y=sin（x﹣） 再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是y=sin （x﹣）． 故选C． 点评：本题主要考查三角函数的平移变换．平移的原则是左加右减、上加下减． 6．已知A，B，C为△ABC的三个内角，命题p：A=B；命题q：sinA=sinB．则￢p是￢q的（ ） A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 考点：必要条件、充分条件与充要条件的判断． 专题：简易逻辑． 分析： A，B，C为△ABC的三个内角，A=B?sinA=sinB，继而得到p是q的充分必要条件，所以￢p是￢q的充分必要条件．问题得以解决． 解答：解：∵A，B，C为△ABC的三个内角，A=B?sinA=sinB， ∴p?q，q?p， ∴p是q的充分必要条件， ∴￢p是￢q的充分必要条件． 故选：C． 点评：本题以三角形为载体，考查命题充要条件的意义和判断方法，属基础题． 7．若直线x+y=a+1被圆（x﹣2）2+（y﹣2）2=4所截得的弦长为2，则a=（ ） A． 1或5 B．﹣1或5 C． 1或﹣5 D．﹣1或﹣5 考点：直线与圆相交的性质． 专题：直线与圆． 分析：由已知求出圆心到直线的距离，再由点到直线的距离公式列式求得a的值． 解答：解：∵直线x+y=a+1被圆（x﹣2）2+（y﹣2）2=4所截得的弦长为2， ∴圆心（2，2）到直线x+y﹣a﹣1=0的距离为d=． 由点到直线的距离公式得：，解得：a=1或5． 故选：A． 点评：本题考查直线和圆的位置关系，考查了点到直线的距离公式的应用，是基础的计算题． 8．已知向量=（3，﹣4），=（6，﹣3），=（2m，m+1）．若，则实数m的值为（ ） A． B．﹣3 C． D．﹣ 考点：平行向量与共线向量；平面向量的坐标运算． 专题：平面向量及应用． 分析：先求得得==（3，1），再由，则这两个向量的坐标对应成比例，解方程求得实数m 的值，可得结论． 解答：解：由题意可得==（3，1），若， 则这两个向量的坐标对应成比例，即， 解得m=﹣3， 故选：B． 点评：本题主要考查两个向量共线的性质，两个向量坐标形式的运算，属于基础题． 9．对任意实数a，b定义运算“?”：，设f（x）=（x2﹣1）?（4+x），若函数y=f（x）+k 的图象与x轴恰有三个不同交点，则k的取值范围是（ ） A．（﹣2，1） B． [0，1] C． [﹣2，0） D． [﹣2，1） 考点：根的存在性及根的个数判断． 专题：函数的性质及应用． 分析：化简函数f（x）的解析式，作出函数y=f（x）的图象，由题意可得，函数y=f （x）与y=﹣k的图象有3个交点，结合图象求得结果．． 解答：解：当（x2﹣1）﹣（x+4）＜1时，f（x）=x2﹣1，（﹣2＜x＜3）， 当（x2﹣1）﹣（x+4）≥1时，f（x）=x+4，（x≥3或x≤﹣2）， 函数y=f（x）=的图象如图所示： 由图象得：﹣2≤k＜1，函数y=f（x）与y=﹣k的图象有3个交点， 即函数y=f（x）+k的图象与x轴恰有三个公共点； 故答案选：D． 点评：本题主要考查根据函数的解析式作出函数的图象，体现了化归与转化、数形结合的数学思想，属于基础题． 10．P为椭圆+=1上任意一点，EF为圆N：（x﹣1）2+y2=4的任意一条直径，则?的取值范围是（ ） A． [0，15] B． [5，15] C． [5，21] D．（5，21） 考点：椭圆的简单性质． 专题：圆锥曲线的定义、性质与方程． 分析：利用=﹣化简可知?=﹣4，通过a﹣c≤||≤a+c，计算即得结论． 解答：解：?=（+）?（+）=（+）?（﹣）=﹣=﹣4， ∵a﹣c≤||≤a+c，即3≤||≤5， ∴?的范围是[5，21]， 故选：C． 点评：本题考查椭圆的简单性质，注意解题方法的积累，属于中档题． 二.填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡的相应位置. 11．已知直线l1：ax+2y+6=0，l2：x+（a﹣1）y+a2﹣1=0，若l1⊥l2，则a=． 考点：直线的一般式方程与直线的垂直关系． 专题：直线与圆． 分析：由两直线互相垂直，可得两直线系数间的关系，由此列关于a的方程求得a值． 解答：解：∵直线l1：ax+2y+6=0，l2：x+（a﹣1）y+a2﹣1=0，且l1⊥l2， ∴a×1+2（a﹣1）=0，即a+2a﹣2=0，解得a=． 故答案为：． 点评：本题考查了直线的一般式方程与直线垂直间的关系，关键是对垂直条件的记忆与应用，是基础题． 12．已知a＞0，b＞0，且点（a，b）在直线x+y=2上，则2a+2b的最小值为　4　． 考点：基本不等式． 专题：不等式的解法及应用． 分析：点（a，b）在直线x+y=2上，可得a+b=2．再利用基本不等式的性质、指数运算性质即可得出． 解答：解：∵点（a，b）在直线x+y=2上，∴a+b=2． 又a＞0，b＞0， 则2a+2b≥2=2=2=4，当且仅当a=b=1时取等号． ∴2a+2b的最小值为最小值为4． 故答案为：4． 点评：本题考查了基本不等式的性质、指数运算性质，考查了推理能力与计算能力，属于中档题． 13．设m＞1，在约束条件下，目标函数z=x+my的最大值等于2，则m=． 考点：简单线性规划． 专题：不等式的解法及应用． 分析：根据m＞1，可以判断直线y=mx的倾斜角位于区间（）上，由此判断出满足约束条件件的平面区域的形状，再根据目标函数z=x+my对应的直线与直线y=mx垂直，且在直线y=mx 与直线x+y=1交点处取得最大值，由此可得关于m的方程，从而求得m值． 解答：解：∵m＞1，由约束条件作出可行域如图， 直线y=mx与直线x+y=1交于（）， 目标函数z=x+my对应的直线与直线y=mx垂直，且在（）处取得最大值， 由题意可知，又∵m＞1，解得m=1+． 故答案为：1+． 点评：本题考查的知识点是简单线性规划的应用，其中根据平面直线方程判断出目标函数z=x+my对应的直线与直线y=mx垂直，且在（）点取得最大值，并由此列出关于m的方程是解答本题的关键，是中档题． 14．已知sinθ﹣cosθ=，θ∈（0，π），则tanθ=． 考点：同角三角函数基本关系的运用． 专题：三角函数的求值． 分析：把已知等式两边平方，利用完全平方公式及同角三角函数间基本关系化简，求出sin θ+cosθ的值，与已知等式联立求出sinθ与cosθ的值，即可确定出tanθ的值． 解答：解：对sinθ﹣cosθ=①，平方得1﹣2sinθcosθ=，即2sinθcosθ=， 由θ∈（0，π），知θ∈（0，）， ∵（sinθ+cosθ）2=1+2sinθcosθ=， ∴sinθ+cosθ=②， 联立①②，解得：sinθ=，cosθ=， 则tanθ=， 故答案为： 点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键． 15．若函数f（x）=x3+a|x﹣1|在[0，+∞）上单调递增，则实数a的取值范围是　[﹣3，0]　． 考点：带绝对值的函数；函数单调性的判断与证明． 专题：函数的性质及应用． 分析：由条件求得f′（x），根据当x≥1时，f′（x）≥0求得a的范围；当0≤x＜1时，f′（x）≥0，求得a的范围．再把2个a的范围取交集，即得所求． 解答：解：函数f（x）=x3+a|x﹣1|=，f′（x）=， ∵f（x）在[0，+∞）上单调递增，当x≥1时，f′（x）=3x2+a≥0，∴a≥﹣3； 当0≤x＜1时，f′（x）=3x2﹣a≥0，∴a≤0． 综上可得，﹣3≤a≤0， 故答案为：[﹣3，0]． 点评：本题主要考查对由绝对值的函数，函数的单调性的性质，属于基础题． 三.解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内. 16．（12分）（2015春?安庆月考）设向量=（sin2x，sin），=（cos，﹣cos2x），f（x）=?． （1）求f（x）的最小正周期； （2）求f（x）在区间[0，π]上的单调递减区间． 考点：两角和与差的正弦函数；平面向量数量积的运算． 专题：三角函数的图像与性质；平面向量及应用． 分析：（1）由条件利用两个向量的数量积公式求得f（x）的解析式，再根据正弦函数的周期性得出结论． （2）由条件根据正弦函数的单调性求得f（x）的减区间，再结合x∈[0，π]，进一步确定函数的减区间． 解答：解：（1）由题意可得f（x）=?=sin2xcos﹣sincos2x=sin（2x﹣）， 故函数的最小正周期为=π． （2）令2kπ+≤2x﹣≤2kπ+，求得kπ+≤x≤kπ+， 故函数的减区间为[kπ+，kπ+]，k∈z． 再根据x∈[0，π]，可得函数的减区间为[，]． 点评：本题主要考查两个向量的数量积公式，三角函数的恒等变换，正弦函数的周期性和单调性，属于中档题． 17．（12分）（2015春?安庆月考）公差d＞0的等差数列{an}中，a1=2，a1、a2、a4成等比数列； （1）求数列{an}的通项公式； （2）数列{bn}满足an=+++…+，求数列{bn}的通项公式． 考点：数列递推式；等比数列的性质． 专题：等差数列与等比数列． 分析：（1）利用（a1+d）2=a1（a1+3d），计算即得结论； （2）通过an=+++…+与an﹣1=++…+作差，结合an=2n、计算即得结论． 解答：解：（1）∵a1、a2、a4成等比数列， ∴（a1+d）2=a1（a1+3d）， 整理得：d=a1=2， ∴an=a1+（n﹣1）d=2n； （2）∵an=+++…+…①， ∴an﹣1=++…+…②． ①﹣②得：an﹣an﹣1=（n≥2）， 又∵an=2n， ∴bn=2（2n+1）=2n+1+2（n≥2）， 当n=1时，b1=6适合上式， ∴bn=2（2n+1）=2n+1+2． 点评：本题考查数列的通项，注意解题方法的积累，属于中档题． 18．（12分）（2014春?芜湖期末）△ABC中内角A、B、C的对边分别为a、b、c，且2acosC=2b ﹣c． （Ⅰ）求角A的大小； （Ⅱ）如果a=1，求b+c的取值范围． 考点：正弦定理；余弦定理． 分析：（Ⅰ）利用正弦定理以及两角和与差的三角函数，化简方程，即可求角A的余弦值，得到A的值； （Ⅱ）利用正弦定理区别b，c的值，b+c为B的正弦函数，通过三角函数值域，求出b+c 的取值范围． 解答：解：（Ⅰ）2acosC=2b﹣c，由正弦定理可得：sinAcosC+sinC=sinB， sinB=sin（A+C）=sinAcosC+cosAsinC．∴sinC=cosAsinC，∵sinC≠0， ∴cosA=， 角A的大小为：； （Ⅱ）由正弦定理可得：b=，， ∴b+c===， ∵∴， ∴∈， ∴， ∴b+c的取值范围：（1，2]． 点评：本题考查正弦定理的应用，三角函数的化简求值，函数的值域的应用． 19．（13分）（2015春?哈尔滨校级期中）已知函数f（x）=lnx﹣ax，其中a＞0． （1）当a=1时，求f（x）在[1，e]上的最大值； （2）若1≤x≤e时，函数f（x）的最大值为﹣4，求函数f（x）的表达式． 考点：利用导数求闭区间上函数的最值． 专题：导数的概念及应用． 分析：（1）将a=1代入，求出函数f（x）的导数，从而求出函数的单调区间和最值； （2）通过讨论a的范围，结合函数的单调性以及f（x）max=﹣4，从而求出a的值，进而求出函数的表达式． 解答：解：f′（x）=﹣a=，（a＞0，x＞0） （1）当a=1时，f′（x）=， ∴x∈[1，e]时，f′（x）＜0， ∴f（x）在[1，e]上单调递减，最大值为f（1）=﹣1． （2）∵f′（x）=﹣a， 令f（x）在（0，）上单调递增，在（，+∞）上单调递减． ①当0＜＜1，即a＞1时，f（x）max=f（1）=﹣4，解得a=4符合题意； ②当1≤≤e，即≤a≤1时，f（x）max=f（）=﹣4，解得：a=e3＞1（舍去）； ③当＞e，即0＜a＜时，f（x）max=f（e）=﹣4，解得：a=＞（舍去）． 综上，f（x）=lnx﹣4x． 点评：本题考查了函数的单调性、最值问题，考查导数的应用，是一道中档题． 20．（13分）（2015春?安庆月考）已知数列{an}的前n项和为Sn，a1=1，an+1=2Sn+1（n∈N*）． （1）求数列{an}的通项公式； （2）求数列{}的前n项和Tn． 考点：数列的求和；数列递推式． 专题：等差数列与等比数列． 分析：（1）通过an+1=2Sn+1与an=2Sn﹣1+1（n≥2）作差、整理可知数列{an}是首项为1、公比为3的等比数列，进而计算可得结论； （2）通过an=3n﹣1可知=，利用错位相减法计算即得结论． 解答：解：（1）∵an+1=2Sn+1（n∈N*）， ∴an=2Sn﹣1+1（n≥2）， 两式相减得：an+1=3an（n≥2）， 由an+1=2Sn+1得：a2=2a1+1=3， ∴a2=3a1满足上式， ∴数列{an}是首项为1、公比为3的等比数列， ∴an=3n﹣1； （2）∵an=3n﹣1， ∴=， ∴Tn=++…++， ∴Tn=++…++， 两式相减得：Tn=3+2（++…+）﹣=4﹣， ∴Tn=6﹣． 点评：本题考查数列的通项及前n项和，注意解题方法的积累，属于中档题． 21．（13分）（2012?长春模拟）如图，椭圆经过点（0，1），离心率． （l）求椭圆C的方程； （2）设直线x=my+1与椭圆C交于A，B两点，点A关于x轴的对称点为A′（A′与B不重合），则直线A′B与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由． 考点：椭圆的标准方程；直线与圆锥曲线的综合问题． 专题：综合题；压轴题． 分析：（1）把点（0，1）代入椭圆方程求得a和b的关系，利用离心率求得a和c的关系，进而联立方程求得a和b，则椭圆的方程可得 （2）把直线方程与椭圆方程联立消去y，设出A，B的坐标，则A′的坐标可推断出，利用韦达定理表示出y1+y2和y1y2，进而可表示出A′B的直线方程，把y=0代入求得x的表达式，把x1=my1+1，x2=my2+1代入求得x=4，进而可推断出直线A′B与x轴交于定点（4，0）． 解答：解：（1）依题意可得，解得a=2，b=1． 所以，椭圆C的方程是； （2）由 得（my+1）2+4y2=4，即（m2+4）y2+2my﹣3=0， 设A（x1，y1），B（x2，y2） 则A′（x1，﹣y1）． 且． 经过点A′（x1，﹣y1）， B（x2，y2）的直线方程为． 令y=0，则 又∵x1=my1+1，x2=my2+1．∴当y=0时， 这说明，直线A′B与x轴交于定点（4，0）． 点评：本题主要考查了椭圆的标准方程，直线与椭圆的位置关系．考查了学生基础知识的综合运用．。

正视图俯视图侧视图安庆2015届高三年级第三次模拟考试数学(文科)试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试时间120分钟。

注意事项：1．答题前，务必在试题卷答题卡规定的地方填写自己的班级、姓名、考场号、座位号。

2．答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3．答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰。

作图题可先用铅笔在答题卡规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚。

必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效。

4．保持卡面清洁，不折叠，不破损。

第I 卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的.1．设i 是虚数单位，则复数324321i i i -+-等于（ ） A ．i 62-- B ．i 22+- C ．i 24+ D ．i 64-2．已知集合{}04|2>-=x x A ，{}02|<-=x x B ，则()B A C R ⋂等于（ ） A ．)2,(-∞B ．[]2,2-C ．()2,2-D ．)2,2[-3．“3=m ”是“函数m x x f =)(为实数集R 上的奇函数”的（ ）.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4．在区间[]0,π上随机取一个实数x ，使得1sin 0,2x ⎡⎤∈⎢⎥⎣⎦的概率为（ ）A ．1πB ．2πC ．13D ．235．将函数π()sin(2)3f x x =+的图象向右平移ϕ个单位，得到的图象关于原点对称，则ϕ的最小正值为（ ）A ．π6B ．π3C ．5π12 6．已知某几何体的三视图，则该几何体的体积是（A ．12B ．24C ．36D ．482 3 5 5 7 920 1 4 810 3 3 4 534 1 2 2 56 97．直线10x my ++=与不等式组30,20,20x y x y x +-≥⎧⎪-≥⎨⎪-≤⎩表示的平面区域有公共点，则实数m 的取值范围是（ ）A ．14,33⎡⎤⎢⎥⎣⎦B ．41,33⎡⎤--⎢⎥⎣⎦C ．3,34⎡⎤⎢⎥⎣⎦D ．33,4⎡⎤--⎢⎥⎣⎦8．已知圆心为O ，半径为1的圆上有不同的三个点C B A ,,，其中0=⋅OB OA ，存在实数,λμ满足0=++OB u OA OC λ，则实数,λμ的关系为（ ） A ．221λμ+= B ．111λμ+= C ．1λμ= D ．1λμ+=9．已知抛物线28y x =的准线与双曲线()222210,0x y a b a b-=>>相交于A 、B 两点，双曲线的一条渐近线方程是y x =，点F 是抛物线的焦点，且△FAB 是等边三角形，则该双曲线的标准方程是（ ）A ．183222=-y xB ．221163x y -=C ．221632x y -=D ．221316x y -= 10．对于函数()x f x ae x =-，若存在实数,m n ，使得()0f x ≤的解集为[](),m n m n <，则实数a 的取值范围是（ ）A ． ()1,00,e ⎛⎫-∞⋃ ⎪⎝⎭B ． ()1,00,e ⎛⎤-∞⋃ ⎥⎝⎦C ．10,e ⎛⎫⎪⎝⎭D ． 10,e ⎛⎤⎥⎝⎦第II 卷（非选择题，共100分）二、填空题：本大题共5小题，每小题5分，共25分，把答案填在题中横线上。

文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第I 卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1．已知集合11,22A ⎧⎫=⎨⎬⎩⎭,集合{}2,B y y x x A =|=∈,则AB =( )(A )12⎧⎫⎨⎬⎩⎭(B ){}2 (C ){}1 (D )φ 2. 已知i 是虚数单位,若()32i z i -⋅=,则z =( )(A )1255i - (B )2155i -+ (C )2155i -- (D )1255i +3. 下列函数中,在区间()0,+∞上为增函数的是( ) (A )()ln 1y x =- (B )1y x =-(C )13xy ⎛⎫= ⎪⎝⎭(D )sin 2y x x =+4.抛物线214y x =-的焦点坐标是( ) (A )()1,0- (B )()2,0- (C )()0,1- (D )()0,2- 5.将函数sin y x =的图象上所有的点向右平移10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( ) (A )sin 25y x π⎛⎫=-⎪⎝⎭(B ) sin 210y x π⎛⎫=-⎪⎝⎭(C )1sin 210y x π⎛⎫=-⎪⎝⎭ (D )1sin 220y x π⎛⎫=- ⎪⎝⎭6.已知A ,B ,C 为ABC ∆的三个内角,命题p :A B =;命题q :sin sin A B =.则p ⌝是q ⌝的( ) (A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件7.若直线1x y a +=+被圆()()22224x y -+-=所截得的弦长为则a =( ) (A )1或5 (B )1-或5 (C )1或5- (D )1-或5-8.已知向量()3,4OA =-,()6,3OB =-,()2,1OC m m =+,若AB ∥OC ,则实数m 的值为( )(A )15 (B )35- (C )17- (D )3-9.对任意实数a 、b ,定义运算“⊙”：a ⊙b ,1,1b a b a a b -≥⎧=⎨-<⎩，设()()21f x x =-⊙()4x k ++，若函数()f x 的图像与x 轴恰有三个公共点，则k 的取值范围是（ ） (A )()2,1- (B )[]0,1 (C )[)2,0- (D )[)2,1-10. P 为椭圆2211615x y +=上任意一点，EF 为圆()22:14N x y -+=的任意一条直径，则 PE PF ⋅的取值范围是（ ）(A )[]0,15 (B )[]5,15 (C )[]5,21 (D )()5,21第II 卷(非选择题 共100分)二.填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置.11．已知直线1:260l ax y ++=，()22:110l x a y a +-+-=，若12l l ⊥，则a =＿＿。

安徽省示范高中2015届高三第三次联考金榜教育·2015届安徽省示范高中高三第三次联考数学（文科）参考答案一：选择题1 【答案】C2 【答案】A 【解析】时，，，。

反之不成立，也可以。

故选A。

3 【答案】B【解析】5127 cos sin-+131313αα-==.4 【答案】A【解析】由na==，所以12(21)(32)(1)5na a a n n+++=-+-+++-=，即，即，解得.选A.5【答案】D【解析】由五点作图法知，= -6 【答案】D【解析】依题意，函数对称轴为,且在上为增函数，因为，，，所以,即选择D.7【答案】A【解析】特称命题的否定为：对任意实数，都有，选；8【答案】A【解析】0000000sin sin75sin(3045)sin30cos45sin45cos304A==+=+=由可知, ,所以,由正弦定理得1sin2sin24ab BA=⋅==,故选A9【答案】D【解析】建立如图所示的直角坐标系，则()()()()0,0,0,4,2,4,4,0A B C D，从而，故()()3,2,3,2PA PB=--=-，从而。

10【答案】D【解析】方法一：时，在上单调递增，符合题意。

若则22()(2)24g x k x kx=--+在上单调递增，若，此时符合题意；若则且，解得，所以的取值范围是。

方法二：求导得''2(),()2(2)2f x kg x k x k==--，若显然符合题意，若，当则，即时符合题意，否则，且'2()2(2)20g k k k k =--≥，化简得232(2)0300k k k k ⎧->⎪-≥⎨⎪<⎩，解得，所以实数的取值范围是，选D 。

二：填空题 11【答案】【解析】222||()()2||||2||||cos 7||73a b a b a b a a b b a b a b a b a b π+=++=++=++=⇒+=. 12【答案】【解析】，所以，((0)+3)(1)f f f e ==. 13【答案】【解析】由题设及正弦定理，所以2221cos 22b c aA bc +-==，. 14【答案】【解析】由题意得，又，得，设等比数列的公比为，可得，解得，，。

资料概述与简介 语文试题 本试卷分为第I卷（阅读题）和第II卷（表达题）。

全卷满分150分，考试时间150分钟。

第I卷（阅读题，共66分） 一、阅读下面的文字，完成1~3题。

（9分） 城乡文化的交融 过去，社会文化同生活方式一样，也可以分为城市文化和乡村文化，两者之间似乎泾渭分明。

城市文化认为乡村文化缺乏文化含量，而乡村文化则认为城市文化缺少生活气息。

改革开放以来，在市场经济的推动下，我国城市化以前所未有的速度发展，城市文化与乡村文化之间的关系也发生了根本的变化，逐渐由界线分明走向相互渗透，趋于统一。

其中农村文化更多地表现出向城市文化靠拢的趋势。

当然，这种统一并不是简单地将乡村文化包容在城市文化之中。

实际上，两者之间的融合经历了一个复杂的过程，在这一过程之中，乡村文化和城市文化都经历了根本的变化。

应该说，在这个过程中，乡村文化的确呈现出衰落的迹象，如在广大农村，许多地方存在着自己的地方戏曲，它们代表了不同地方的“文化风味”，是乡村文化的重要组成部分。

但在城市文化的猛烈冲击下，这些地方戏曲日益失去了往日的吸引力，特别是对青年的吸引力。

现在的农村青年和城市青年一样，喜欢的是流行歌曲，在此情况下，一些地方戏曲，特别是一些小的地方戏曲的衰落就是难免的。

但是，大凡为历代所传承的文化都不会如此脆弱。

我们看到，有些地方文化在与城市文化的交融中脱颖而出。

而且某些乡村文化在逐渐融入城市文化，并成为城市文化的一个组成部分。

如东北大秧歌一直是东北乡村流行的一种文化形式，但在今天，人们更多地是通过电视看到大秧歌。

而这些节目的制作者，是戴着大众的“眼镜”来生产这些节目的。

到最后，连跳大秧歌的人都认为，电视上的大秧歌是“标准”的大秧歌。

这样，经过改造的大秧歌已不再是原来意义上独立存在的乡村文化，而成了城市大众文化的一个组成部分和构成要素了。

再看城市文化。

如果说城市化的进程对于乡村文化来说是一个衰落过程的话，那么它对于城市文化而言则是一个扩张的过程。

2015年皖北协作区高三年级联考参考答案数学（文科）一、选择题1A、2B、3D、4C、5A、6C、7D、8C、9A、10D、二、填空题11、 25； 12、 9； 13、8 ； 14、,2()2()-∞-∞，＋； 15、①③④⑤ 三、解答题16．解：(1)由正弦定理，得3sin cos B C ＝()sin 13cos C B -化简可得 sin 3sin()C B C =+又A ＋B ＋C ＝π，所以sin C ＝3sin A ，因此sin sin A C ＝13. --------------------------6分 (2)由sin sin A C ＝13得c ＝3a . 由余弦定理及cos B ＝16得 b 2＝a 2＋c 2－2ac cos B ＝a 2＋9a 2－6a 2×16＝9a 2. 所以b ＝3a .又a ＋b ＋c ＝14.从而a ＝2，因此b ＝6. -----------------------------12分17.解：(1)因为“综合素质”科目中成绩等级为B 的考生有10人， 所以该考场有10400.25=人 所以该考场考生中“综合素质”科目中成绩等级为A 的人数为400.0753⨯= --------------4分（2）“综合素质”科目成绩为D 的频率为10.0750.2500.3750.2000.1----=所以该考场考生“综合素质”科目的平均分为900.075800.250700.375600.1500.26960⨯+⨯+⨯+⨯+⨯=>所以“综合素质”的考核合格 -----------------8分（3）该考场考生中“服务技能”科目中成绩等级为A 的人数为40(10.3750.3750.1500.025)3⨯----=所以两科考试中，共有6人得分等级为A ，又恰有两人的两科成绩等级均为A ，所以还有2人只有一个科目得分为A ，设这四人为甲，乙，丙，丁，其中甲，乙是两科成绩都是A 的同学，则在至少一科成绩等级为A 的考生中，随机抽取两人进行访谈，基本事件空间为{Ω={甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁}},有6个基本事件设“随机抽取两人进行访谈，这两人的两科成绩等级均为A ”为事件B ，所以事件B 中包含的基本事件有1个，则1()6p B =. -----------------12分 18．（1）证明：如图，取AE 中点M ，连接BM 、F M ． F 是DE 中点，FM ∴是ADE ∆的中位线，//FM AD ∴，且12FM AD =， 又//BC AD ，且12BC AD =，//FM BC ∴且FM BC =， ∴四边形FMBC 是平行四边形，//FC MB ∴．FC ⊄面,ABE MB ⊂面ABE ，//FC ∴平面ABE ． -----------------6分（2）取DH 中点N ，连接FN 、EH ，F 是DE 的中点，1//,=2FN EH FN EH ∴且． ABC ∆是等腰直角三角形，AC BC =，M 是AB 的中点， E H A B∴⊥ 又平面ABCD ⊥平面ABE ，平面ABCD 平面ABE AB =，EH ⊂平面ABCD EH ABCD ∴⊥平面FN ABCD ∴⊥平面 =S 111(12)222212222322DCH ADH BCH S S S ∆∆∆--=⨯+⨯-⨯⨯-⨯⨯=梯形ABCD 又 1222FN EH == 11322133222F DCH DCH V S FN -∆∴==⨯⨯=-----------------12分 或 由F 是ED 的中点且HC HD ⊥，得1112122F DCH E DCH V V HC HD HE --=== -----------------12分 19．解： 11(),31n n n n a a f a a +==+（） DAFC E HBM N1131113,113,n n n n n n a a a a a a +++∴==+∴-=∴数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项，3为公差的等差数列. -----------------6分1(2)113(1)32,1,32n n n n a a n =+-=-∴=-由（）得 -----------------7分111111,323133231n n a a n n n n +⎛⎫⋅=⋅=⋅- ⎪-+-+⎝⎭ 111111134473231n S n n ⎛⎫∴=-+-+⋅⋅⋅+- ⎪-+⎝⎭ 11=(1)33131n n n -=++ -----------------13分20．解：（1）原函数的定义域为()∞+，02'1)(xa x a x f -+=由题意3,1212)2(2'=∴=-+=a a a f -----------------5分 ()'212()ln 1()a g x a x x x a a g x x x x-=---=+- 2221(1)(1)x ax a x x a x x-++---+-== '()011g x x x a ===-由得，或 -----------------7分'112()011()00112()1,1,0,1(1,)11,2()0011,12()0,1(1,);1,110,1,()0,1,a a g x x a g x x x a a g x a a a a g x a a g x a a a a g x ->>><<-<<<>->--+∞-==+∞<-<<<-+∞--≤≤若即时，由得由得或所以时，的增区间为（）减区间为（）,若即时，的减区间为（，）若即时，可得的减区间为（）,增区间为（）若即时的增区间为（）减1+∞区间为（，）综上所述： 2,()1101,a g x a a >--∞+若时的增区间为（，）,减区间为（，1）,（） 2()0a g x =+∞若时，的减区间为（，）2()0,1(1,);1,1a g x a a <<-+∞-若1时，可得的减区间为（）,增区间为（） 1()0,1,(1,)a g x ≤+∞若时，的增区间为（）减区间为 ----------------------13分21．法一：解：（1） 由题意可知m>n>0, 22,.a m b n == 2112c c a =⎧⎪⎨=⎪⎩ 213,1,.24c a b ==∴= 13422=+∴y x 椭圆的方程为 -----------------4分 （2）设0000(,),(0,0),(0,)P x y x y Q t >>，则10220=+n y m x ， 12(,0),(,0)F c F c -1001(,),(,)FP x c y FQ c t ∴=+= 12,F P F Q O ⋅=000y t ∴+=(x +c)c ①2,,P F Q 三点共线00y t x c c∴=-- ② 由①②得0000()0cy c x c y x c-++⋅=- 22200x y c m n -==-即 -----------------------------------9分 220011m n x y m n+=+= 000011x n y nx y =-⎧⎨=⎩∴+=联立可解得 1P x y ∴+=点在定直线上 -------------------------------13分法二：解：（1） 由题意可知m>n>0,因为椭圆焦距为1，所以12=-n m ，43,1,2121==∴=-n m mn m ，所以离心率为 13422=+∴y x 椭圆的方程为 -----------------4分 （2）设)(0,0y x p 为第一象限内椭圆上的点，则10220=+n y m x ， )0,(22n m F F -∴为椭圆的右焦点， 020*********()(0,),(,0)(,)(,)y PF y x m n x m n y m nQ F m n m n x F P x m n y y m nF Q m n m n x ∴=-----∴----∴=+--=---的方程为1220002000,00PF PF O y m n x m n m n m n x y x m n m n x ⋅=--+-+=--∴+-+=--因为所以22000m n x y --+=即 -----------------------------------9分 220011m n x y m n +=+=000011x ny n x y =-⎧⎨=⎩∴+=联立可解得1P x y ∴+=点在定直线上 -------------------------------13分。