2010数学建模A题答案论文 储油罐的变位识别与罐容表标定
- 格式:pdf
- 大小:577.64 KB
- 文档页数:21

储油罐的变位识别与罐容表标定的积分方程模型摘要:本文通过建立积分方程组模型:()()()()()()()()()()()()()1110022010313120444235454334,0,0,,cos ,,cos ,,cos ,,x d H C V x h x x H x H C V x h x H x H x H C V H S A x B x dx h x H x H x H C C V H x h x H x H C C V H x h x h H H x H ααα==≤≤⎧⎪-⎪==≤≤⎪⎪-⎪=+--=≤≤⎨⎪⎪-=--=≤≤⎪⎪=--=≤≤⎪⎩⎰刻画、描述和揭示了储油罐由于地基变化而引起的罐体变位时储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系。
合理的假设当储油罐在软土地基所加荷载不大时,地基变形小;当荷载增大到一定程度后.油罐地基沉降速率变快,由于地基内孔隙水来不及消散,地基变形保持体积不变,导致土体侧向移动,从而引起远罐地表土隆起,近罐地表土沉降,随着荷载的增加和时间的延续,地基内孔隙水压力逐渐消散,土体固结而产生沉降,使得隆起的地表又逐渐下沉,经过一段时间后,趋于稳定,即储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系曲线就是先是有坡度的,然后有一个平缓的部分,还有一个有坡度的部分。
再利用非线性回归分析的方法通过附表中的数据将α与β非线性拟合出来 ,且拟合效果高度逼近理论结果,从而在模型中任意给出重要参数()S x (油面横切面的面积),1l (倾斜时油箱左下顶点到油位探针底部的距离),2l (倾斜时油位探针底部距油箱右下顶点的距离), 3l (倾斜时油箱右上顶点到油面的距离)的值,便可以描述出储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系。
以此为基础,给出了两个问题较完备的答案。
关键词:积分方程;非线性回归分析;非线性拟合;油面高度;罐容表标定刻度一 问题的重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。

基于微元法的变位储油罐罐容表标定问题摘要加油站当地下储油罐发生一定程度变位时,需要重新标定其罐容表,优化“油位计量管理系统”,目的是得到地下储油罐内油量的真实值,所以研究该问题对加油站具有重要意义。
本文主要利用微元法建立积分模型,解决了储油罐的变位识别与罐容表标定的问题,得到了实验储油罐变位后罐容表新的标定值,实际储油罐变位后储油量与油位高度及变位参数之间的关系,以及实际储油罐变位后罐容表新的标定值。
问题一中,首先对纵向倾斜的小椭圆油罐进行分析,将油罐从罐中无油到加满油的过程分为7个部分来分析,分别是:(1)从罐中无油到将油加到刚好不接触油浮子;(2)从油开始接触油浮子到油灌满倾斜角但刚好不接触罐右侧壁;(3)从罐中油开始接触右侧壁到油灌到左侧壁中点水平线;(4)油从左侧壁中点灌到左侧壁终点水平线;(5)油从左侧壁终点灌到右侧壁中点水平线;(6)油从右侧壁中点灌到油浮子刚好显示油满;(7)从油浮子刚好显示油满到将油罐灌满。
分别分析这7个加油的过程,建立模型,用微元法求解每个部分罐中油体积的变化,根据体积的变化得到油面高度的变化,将变位后的油面高度与无变位时的油面高度作比较,分析得出变位对罐容表的影响。
最后由变位后油面的高度,用Matlab编程序得到变位后罐容表新的标定值。
问题二中,经过对实际储油罐的形状与倾斜及偏转角度情况的分析,我们利用割补法建立罐体变位后的数学模型,先分别分析储油罐只纵向倾斜和只横向偏转的情况,用h的函数关系式,再分析储油罐同时纵向倾微元法得到罐中油体积与变位后罐容表刻度斜和横向偏转的情况,我们将模型转变为先将储油罐横向偏转,然后在横向偏转的基础上再纵向倾斜,由所给的实际储油罐的数据,分别结合只进行纵向倾斜和只进行横向偏转的情况,用拟合的方法,利用Simpson公式,近似得到了倾斜角α=4.5230,偏转角β=1.220。
在α和β确定之后,罐内储油量与油位高度及倾斜角α、偏转角β的关系式即转化为油体积与油位高度的关系式,进而计算得到变位后油位间隔为10cm的罐容表新标定值。

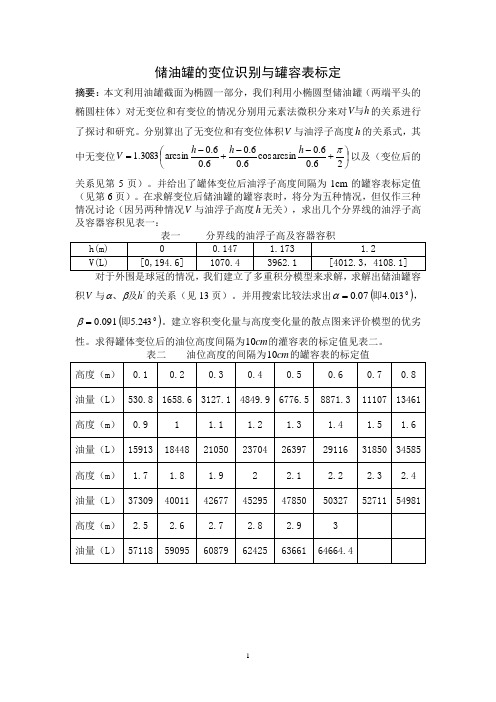
储油罐的变位识别与罐容表标定摘要:本文利用油罐截面为椭圆一部分,我们利用小椭圆型储油罐(两端平头的椭圆柱体)对无变位和有变位的情况分别用元素法微积分来对h V 与的关系进行了探讨和研究。
分别算出了无变位和有变位体积V 与油浮子高度h 的关系式,其中无变位⎪⎭⎫⎝⎛+--+-=26.06.0arcsincos 6.06.06.06.0arcsin3083.1πh h h V 以及(变位后的关系见第5页)。
并给出了罐体变位后油浮子高度间隔为1cm 的罐容表标定值(见第6页)。
在求解变位后储油罐的罐容表时,将分为五种情况,但仅作三种情况讨论(因另两种情况V 与油浮子高度h 无关),求出几个分界线的油浮子高及容器容积见表一:积V 与‘及、h βα的关系(见13页)。
并用搜索比较法求出07.0=α()0013.4即,091.0=β()0243.5即。
建立容积变化量与高度变化量的散点图来评价模型的优劣性。
求得罐体变位后的油位高度间隔为cm 10的灌容表的标定值见表二。
1.问题的提出加油站是一个地区在机动车辆运行系统中必不可少的元素。
而通常加油站都有若干个储存燃油的地下储油罐,且采用流量计和油位计来测量进与出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
但实际情况是:由于储油罐在使用一段时间后,由于地基变形等原因,会使罐体的位置会发生纵向倾斜和横向偏转等变化,从而导致罐容表发生改变。
所以需要对罐容表进行重新标定。
其中,给出了图1 一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2 其罐体纵向倾斜变位的示意图,图3 罐体横向偏转变位的截面示意图。
图4 小椭圆型储油罐(两端平头的椭圆柱体)。
(1)为了掌握罐体变位对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。

全国大学生数学建模竞赛A题获奖—储油罐的变位识别与罐容表标定2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是:A题储油罐的变位识别与罐容表标定我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):日期:2010年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型,在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据,最后分析误差及评价模型的合理性。
对于问题一的任一种情形,我们均建立笛卡尔坐标系,当储油罐无变位时,利用微元法得到体积关于h的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。

12010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数, 并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
(先检测误差补偿的可靠性,然后进行计算0-10,10-20…..)附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据地平线 图1 储油罐正面示意图油位探针2误差补偿公式:油位探针地平线 图2 储油罐纵向倾斜变位后示意图(b) 小椭圆油罐截面示意图水平线1.2m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线油位探针(a )无偏转倾斜的正截面图。
题目: 储油罐的变位识别与罐容表标定【摘 要】本文根据题目要求,针对具体问题建立相应的数学模型,并对问题进行精确求解,逐层深入比较题给数据与理论求解值同时分析它们之间的关系,据此得出合理的结论。
对于问题一,首先,采用截面法建立数学模型对无变位及有变位的理论油容量与油位高度之间的关系表达式。
然后,根据附件1所给的无变位进油时油高求出对应理论油量并与所给实际油量值相比较,发现两者的相对偏差σ基本成一稳定值3.371%,并根据两者之间的关系求出理论油量的修正函数,同时将偏差函数运用于无变位出油中,通过比较相邻两时刻绝对出油量的相对误差(均值为41021.3-⨯)检验修正函数的正确性。
接着,根据对应倾斜变位进油油高的校正理论油量与实际油量相比较,分析得出纵向变位时液位较小时罐容表读数偏小,液位较高时读数偏大的结论。
最后运用MATLAB 编写程序对变位后罐容按油位高度间隔为1cm 的进行标定,结果见附表1。
对于问题二,由于横向倾斜不影响体积的计算,只影响油面高度实际值h 与罐容表测量值*h 之间的关系。
于是,先根据三重积分与截面法计算只有纵向倾斜的情况下罐容与倾斜角度α和h 的关系),(h f V y α=。
然后,根据油面高度与横向偏转角度β及*h 关系),(*h f h β=得罐内储油量与油位高度及纵向倾斜角度α和横向偏转角度β之间的一般关系),,(*h f V y βα=。
取0,0==βα(无变位时),根据附件2中油位高度计算出相应油量,发现与附件所给油量容积几乎完全一致。
接着利用附件2中实际出油量与理论出油量的差值的平方和最小的条根据误差最小原则选取)244.4,129.2(==βα,求得罐容表标定值部分数据量与理论出油量近似相等,验证模型的正确性和可靠性。
并进行了模型推广,进行了基于MATLAB 的GUI 设计。
关键词:截面法,三重积分,遍历法,NDEPSO 算法,GUI 设计一问题的重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):A我们的参赛报名号为(如果赛区设置报名号的话):J0901所属学校(请填写完整的全名):西北工业大学参赛队员(打印并签名) :1. 王艺霖2. 卜千3. 孟阅然指导教师或指导教师组负责人(打印并签名):彭国华日期: 2009 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要解决储油罐的变位识别与罐容表标定问题的核心是寻求在不同状态下油位高度与对应罐容的函数关系。
针对问题一,利用椭圆柱体的对称特征,在确定变位后油位高度与不变位的油位高度的内在关系基础上,将变位后的罐容的求解转化为对应的不变位的罐容的求解,大大简化了其计算难度,并且得到了罐容与油位高度的解析表达式;进一步得到罐体变位后使罐容表整体往上或往下移动这一结论,同时给出了相应变位角的罐容表标定值。
在进行了误差数值和原因多方面分析后,使用修正补差方法,顺利地减小了误差。
针对问题二,通过计算分析,发现球冠体的积分很难得到一个显式解析式,因此,采用数字积分的方法解决本问题。
首先,根据油位高度及附近的几何关系,及体积变化速率/V h ∆∆最大处的角度关系,建立起α、β与进/出油量、显示油量容积之间的等式,进而解出 2.1α≈︒和 4.3β≈︒的结果;然后,将其代入罐容模型,采用复合Simpson 算法近似计算体积积分,得到修正罐容表,并与进/出油量进行比较,得出相对误差,检验模型的正确性与可靠性。
储油罐的变位识别和罐容表标定随着科学技术和社会经济的发展,目前业界公认的油站有液位测量设备磁制伸缩型液位仪因其在测量精度及灵敏度为其他测量方法无法比拟而在油品零售行业普遍使用。
而通常的加油站都有若干储存燃油的储油罐。
可是,由于储油罐的地基变形等原因,使罐体的位置发生变化,从而导致罐容表发生改变。
因此,我们针对解决储油罐的变为识别与罐容表标定问题建立相关数学模型,并进行了分析讨论。
对于问题一,要掌握罐体变位后对罐容表的影响,序言将罐体的变位前后罐内油高测值代入罐容表查得相应的油高罐容值,以确定罐中油品的体积量变化情况,得到合理的评价变位后罐容表影响的体系。
我们从罐体的位置没发生变化和发生变化后两个方面进行考虑,利用数学方法中的微积分通过计算得到罐体变化后罐中油品的体积量,再与原罐中油品的体积量对比、核对。
两种情况下,油品的体积量误差越小,模型拟合精度越高,同时,由于罐容标定是每隔1cm 确定一个容积值,这样罐容表中只有整厘米数油高具有对应地容积值,当油高介于整厘米数之间时就需要通过内插法来求取对应的容积值。
对于问题二,要根据实际储油罐,建立罐体变位后表达罐容表罐内储油量与油位高度及实位参数间的关系的数学模型来确定定位参数,也即是一个标准的参数识别问题,那么最小二乘法拟合是解决此类问题的工具。
同理,要得知罐体变位后油位高度间隔为10的罐容表标定值,也需要利内插法求取相应的容积值。
关键词:应用 罐容表 模型拟合 内插法 最小二乘法拟合 容积值椭圆筒的部分容积计算: 椭圆方程为:2222121x y R R += 即y = 液高为2H(CD =2H ) 即 12()y R H =-- 亦即为直线AB 方程将1y 代入椭圆方程得1x =12()y R H =--液体截面面积为:()1210x S H R dx ⎡=-+⎢⎣⎰2211121)]sin H R R H R R -=-+-由图212.05t 0.40H α--⎰⎰知, WP H = 1QO L = QG D = 0C O L = 1()cos FW Q H α=- FP =cos D αWP FD FW =-=1()cos cos D D H αα-- 则1()cos cos D H D H αα=--,整理得:21tan cos H H D αα=- AB 为倾斜时的液面,矩形面积 2SEKOC H L = 在梯形ABOC 中,11tan BO H L α=+ tan AC BO L α=- t a n A C B O L α=- 梯形的面积1()2ABOC S BO AC L =+ 令 11tan N N L α=+则 1(tan )2ABOC S N N Lg L α=+- 1(2tan )2N L L α=- 因ECOK ABOC S S =则21(tan )2H L N L L α=- 即2tan 2L H N α=- (1) 将:2111tan tan tan cos H N H L D L αααα=+=-+ 代入(1)得:221tan ()tan cos 2H L H D L ααα=-+- 若液面降至如图1 的1CM 以下,利用矩形面积等于直角三角形面积的方法导出2H 与H 的系,这时,矩形底长小于L ,矩形和三角形底长均为tan N α,矩形面积2S H Nlot α= 直角三角形的面积21cot 2S N α=12.05tan 0.40H α--⎰⎰。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):A我们的参赛报名号为(如果赛区设置报名号的话):J0901所属学校(请填写完整的全名):西北工业大学参赛队员(打印并签名) :1. 王艺霖2. 卜千3. 孟阅然指导教师或指导教师组负责人(打印并签名):彭国华日期: 2009 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要解决储油罐的变位识别与罐容表标定问题的核心是寻求在不同状态下油位高度与对应罐容的函数关系。
针对问题一,利用椭圆柱体的对称特征,在确定变位后油位高度与不变位的油位高度的内在关系基础上,将变位后的罐容的求解转化为对应的不变位的罐容的求解,大大简化了其计算难度,并且得到了罐容与油位高度的解析表达式;进一步得到罐体变位后使罐容表整体往上或往下移动这一结论,同时给出了相应变位角的罐容表标定值。
在进行了误差数值和原因多方面分析后,使用修正补差方法,顺利地减小了误差。
针对问题二,通过计算分析,发现球冠体的积分很难得到一个显式解析式,因此,采用数字积分的方法解决本问题。
首先,根据油位高度及附近的几何关系,及体积变化速率/V h ∆∆最大处的角度关系,建立起α、β与进/出油量、显示油量容积之间的等式,进而解出 2.1α≈︒和 4.3β≈︒的结果;然后,将其代入罐容模型,采用复合Simpson 算法近似计算体积积分,得到修正罐容表,并与进/出油量进行比较,得出相对误差,检验模型的正确性与可靠性。