下载文档原格式
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A我们的参赛报名号为（如果赛区设置报名号的话）：A甲1112所属学校（请填写完整的全名）：中国海洋大学参赛队员(打印并签名) ：1. 刘光鹏2. 刘红阳3. 孙迪指导教师或指导教师组负责人(打印并签名)：指导教师组日期： 2010 年 9 月 13 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：储油罐的变位识别与罐容表标定模型摘要针对两种卧式储油罐变位后的标定问题，本文利用微分思想、数值逼近、拟合的原理，建立了卧式罐不变位和变位时的油量随油高模型。
针对小椭圆油罐，首先，根据几何特征写成体积的积分式。
然后，将积分变量离散化，用MATLAB的编程计算实现了规定1cm的等间距油高时精确的罐内油量。
给出了间隔1cm的变位后的标定表（见附录一）。
针对实际储油罐，首先在未发生变位时，同样利用积分知识通过组合形式写出积分表达式。
然后将变量离散化求的很小的间隔内油量值，并用3次多项式逼近作为表达式，通过MATLAB画图发现拟合较好。
当发生变位时，利用近似的体积等价法，将变位油高等价一个未变位高度。
利用积分表达式计算，并通过相邻的油位高度与实际体积之间的关系，求得α的平均值为0.033弧度，β平均值为0.035弧度，但考虑到具体情况不能简单的认为β就是0.035。
储油罐的变位识别与罐容表标定摘 要本文对A 试题进行了分析和研究。
为了解决加油站中储油罐的变位识别与罐容表标定问题，同时分析罐体变位对罐容表的影响，通过建立出在不同油位值情况下比较精准的罐内油位高度与储油量的函数关系模型，利用采集到的小椭圆型储油罐和实际储油罐的实验数据，借助相关软件对问题进行深入研究。
针对问题一：为了研究罐体变位后对罐容表的影响，本文首先根据所给的简化小椭圆型储油罐（两端平头的椭圆柱体），利用微元法，建立出在不同油位值情况下的平头罐体油位高度与储油量的函数对应关系——积分模型（模型一）。
对于倾斜角为 4.1a =︒的纵向变位情况，通过等面积法找到倾斜时油标显示值H 1与对应同体积的水平状态下液高2H 的函数关系，从而得出倾斜角为 4.1a =︒时罐内油位高度与储油量的函数关系。
利用添加多项式对模型进行校正，用MATLAB 软件编程得到所加多项式的参数，得到贴近实际的油位高度与储油量的数学关系模型，并运用该模型得到初始油标值为0，间隔1cm 的罐容表标定值。
再用SPSS 软件中的曲线估计过程拟合得到小椭圆储油罐无变位时油位高度与储油量的函数关系，求解得到无变位时的罐容表。
通过比较小椭圆储油罐无变位和变位斜角为 4.1a =︒时的罐容表标定值，分析出罐体变位前后储油量最大差值大约为270L ，较小差值65L ，平均差值为178.87L ，说明小椭圆罐体变位后对罐容表的影响是很大的。
针对问题二：研究主体为圆柱体、两端为球冠体的实际储油罐，对其进行分段计算，主体1V 的求法沿用问题一中所建立的分段函数数学模型，两端球冠体采用近似椭球的体积求法。
建立出含有参数纵向倾斜角度α和横向偏转角度β的实际罐体显示与储油量的函数对应关系——积分模型（模型二）。
并根据所给采集数据在MATLAB 软件中利用最小二乘法估计出变位参数角度α和β的数值： 2.779, 4.693αβ==将得到的α和β估计值代入模型二中的分段函数关系式中，通过计算理论的累加出油量与检测数据的累加出油量差值，用SPSS 软件中的曲线估计过程拟合得到罐内探针、管线等所占的体积与显示油高的函数关系，并作为修正因子带入的建立的模型二中，得到修正后的模型二（实际罐体显示油高与储油量的函数关系式）。
储油罐的变位识别与罐容表标定的积分方程模型摘要：本文通过建立积分方程组模型：()()()()()()()()()()()()()1110022010313120444235454334,0,0,,cos ,,cos ,,cos ,,x d H C V x h x x H x H C V x h x H x H x H C V H S A x B x dx h x H x H x H C C V H x h x H x H C C V H x h x h H H x H ααα==≤≤⎧⎪-⎪==≤≤⎪⎪-⎪=+--=≤≤⎨⎪⎪-=--=≤≤⎪⎪=--=≤≤⎪⎩⎰刻画、描述和揭示了储油罐由于地基变化而引起的罐体变位时储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系。
合理的假设当储油罐在软土地基所加荷载不大时，地基变形小；当荷载增大到一定程度后．油罐地基沉降速率变快，由于地基内孔隙水来不及消散，地基变形保持体积不变，导致土体侧向移动，从而引起远罐地表土隆起，近罐地表土沉降，随着荷载的增加和时间的延续，地基内孔隙水压力逐渐消散，土体固结而产生沉降，使得隆起的地表又逐渐下沉，经过一段时间后，趋于稳定，即储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系曲线就是先是有坡度的，然后有一个平缓的部分，还有一个有坡度的部分。
再利用非线性回归分析的方法通过附表中的数据将α与β非线性拟合出来 ，且拟合效果高度逼近理论结果，从而在模型中任意给出重要参数()S x (油面横切面的面积)，1l (倾斜时油箱左下顶点到油位探针底部的距离)，2l (倾斜时油位探针底部距油箱右下顶点的距离), 3l (倾斜时油箱右上顶点到油面的距离)的值，便可以描述出储油罐内油面高度i H 与罐容表标定刻度()i h x 之间的关系。
以此为基础，给出了两个问题较完备的答案。
关键词：积分方程；非线性回归分析；非线性拟合；油面高度；罐容表标定刻度一 问题的重述通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。
基于微元法的变位储油罐罐容表标定问题摘要加油站当地下储油罐发生一定程度变位时，需要重新标定其罐容表，优化“油位计量管理系统”，目的是得到地下储油罐内油量的真实值，所以研究该问题对加油站具有重要意义。
本文主要利用微元法建立积分模型，解决了储油罐的变位识别与罐容表标定的问题，得到了实验储油罐变位后罐容表新的标定值，实际储油罐变位后储油量与油位高度及变位参数之间的关系，以及实际储油罐变位后罐容表新的标定值。
问题一中，首先对纵向倾斜的小椭圆油罐进行分析，将油罐从罐中无油到加满油的过程分为7个部分来分析，分别是：（1）从罐中无油到将油加到刚好不接触油浮子；（2）从油开始接触油浮子到油灌满倾斜角但刚好不接触罐右侧壁；（3）从罐中油开始接触右侧壁到油灌到左侧壁中点水平线；（4）油从左侧壁中点灌到左侧壁终点水平线；（5）油从左侧壁终点灌到右侧壁中点水平线；（6）油从右侧壁中点灌到油浮子刚好显示油满；（7）从油浮子刚好显示油满到将油罐灌满。
分别分析这7个加油的过程，建立模型，用微元法求解每个部分罐中油体积的变化，根据体积的变化得到油面高度的变化，将变位后的油面高度与无变位时的油面高度作比较，分析得出变位对罐容表的影响。
最后由变位后油面的高度，用Matlab编程序得到变位后罐容表新的标定值。
问题二中，经过对实际储油罐的形状与倾斜及偏转角度情况的分析，我们利用割补法建立罐体变位后的数学模型，先分别分析储油罐只纵向倾斜和只横向偏转的情况，用h的函数关系式，再分析储油罐同时纵向倾微元法得到罐中油体积与变位后罐容表刻度斜和横向偏转的情况，我们将模型转变为先将储油罐横向偏转，然后在横向偏转的基础上再纵向倾斜，由所给的实际储油罐的数据，分别结合只进行纵向倾斜和只进行横向偏转的情况，用拟合的方法，利用Simpson公式，近似得到了倾斜角α=4.5230,偏转角β=1.220。
在α和β确定之后，罐内储油量与油位高度及倾斜角α、偏转角β的关系式即转化为油体积与油位高度的关系式，进而计算得到变位后油位间隔为10cm的罐容表新标定值。
全国大学生数学建模竞赛储油罐地变位识别与罐容表标定参赛学校：重庆工商大学承诺书我们仔细阅读了中国大学生数学建模竞赛地竞赛规则．我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外地任何人（包括指导教师）研究、讨论与赛题有关地问题．我们知道，抄袭别人地成果是违反竞赛规则地，如果引用别人地成果或其他公开地资料（包括网上查到地资料），必须按照规定地参考文献地表述方式在正文引用处和参考文献中明确列出．我们郑重承诺，严格遵守竞赛规则，以保证竞赛地公正、公平性．如有违反竞赛规则地行为，我们将受到严肃处理．我们参赛选择地题号是（从A/B/C/D中选择一项填写）： A我们地参赛报名号为（如果赛区设置报名号地话）：所属学校（请填写完整地全名）：重庆工商大学参赛队员 (打印并签名) ：1．王文姣2．白洋3．吴静指导教师或指导教师组负责人 (打印并签名)：袁德美日期： 2010 年 9 月 13日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编）：储油罐地变位识别与罐容表标定摘要油品地数量管理在油品地经营过程中占有很重要地地位,其中储油罐罐容表地标定是加油站中油品管理地关键.但由于储油罐地长时间使用会导致地基变形,罐体地位置会发生纵向倾斜和横向偏转等变化（以下称为变位）, 从而需要定期对罐容表进行重新标定.因此能够正确地解决好罐容表地标定问题,将会给现实生活中加油站等储油行业地操作带来方便.本文主要解决储油罐地变位识别及罐容表地标定问题.我们根据积分“无限细分,无限求和”地思想,通过建立积分模型,将储油罐划分为无数个连续地椭圆形截面.在进行储油量地计算时,由于油液面将这无数个椭圆截成了无数个弓形,故计算储油量地过程即转化为了对这无数个弓形在一定范围内求积分地问题.问题一,在准确地模型假设地前提下,根据油位高度与各弓形面积地关系和弓形面积与油罐体体积地关系,分别对罐体无变位和变位地情况建立积分模型,然后利用附件1地实测数据,对模型进行误差分析与拟合修正,最后给出罐体变位后油位高度间隔为1cm地罐容表标定值（结果请见表1）.问题二,在问题一地基础上,首先我们同样采用积分地思想求得罐内储油量与油位高度及变位参数（纵向倾斜角度和横向偏转角度）之间地一般关系.然后根据对问题二地模型所求得地数据α=︒，与附件2所给地实际检测数据进行运算可以得到理想地、值，我们求解得出 2.07β=︒.进而利用α，β得到油位高度间隔为10cm地罐容表标定值（结果请见表2）.4.98另外在去掉温度对储油量不会产生影响地假设条件下,我们对模型进行了进一步地改进. 为了消除温度地影响,我们考虑了油品地体积随温度变化地关系.利用经验公式.将油品体积全部转化为固定温度下地数据,然后再进行比较分析.关键词：优化处理；拟合；罐容表标定；微积分模型；最小二乘法.一、问题重述通常加油站都有若干个储存燃油地地下储油罐，并且一般都有与之配套地"油位计量管理系统"，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定地罐容表（即罐内油位高度与储油量地对应关系）进行实时计算，以得到罐内油位高度和储油量地变化情况．许多储油罐在使用一段时间后，由于地基变形等原因，使罐体地位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变．按照有关规定，需要定期对罐容表进行重新标定．在不考虑外界环境地影响下，现解决如下问题：1．为了掌握罐体变位后对罐容表地影响，利用小椭圆型储油罐（两端平头地椭圆柱体），分别对罐体无变位和倾斜角为地纵向变位两种情况做了实验，得出实验数据．并在所得数据地基础上建立数学模型，研究罐体变位后对罐容表地影响，并算出罐体变位后油位高度间隔为1cm 地罐容表标定值．2．在实际情况下，罐体变位后标定罐容表地标定值与理论上是有偏差地，但也存在着一定地联系，因此问题二需要找出罐内储油量与油位高度及变位参数（纵向倾斜角度和横向偏转角度）之间地一般关系．在对实际情况下罐体变位后进/出油过程中地实际检测数据进行分析与运算后，我们建立一数学模型，并通过其确定变位参数，同时求得罐体变位后油位高度间隔为10cm地值．罐容表标定[]1二、问题分析储油罐罐体地变位识别是油位计量管理系统中地重要环节之一，而油品地数量管理是加油站等经营部门地基础工作，同时它又在其经营过程中占有重要地位．目前，由于地基变形等原因，出现了一些不规范地问题．故对罐体变位识别是确定一个规范地、科学地、精确地油位计量管理系统地必要前提．问题一要解决地是小椭圆形罐体纵向倾斜变位后对罐容表地影响问题．对于此类问题，我们通常利用高等数学中地定积分方法来求解．其一般思想为“求和、取极限” []2.我们根据附件1所给出地小椭圆形罐体在无变位和变位时地进/出油量与油位高度地实验数据最后来修正模型．综上所述，先讨论小椭圆形罐体无变位时，储油量与油位高度之间地关系，建立积分模型一并且根据模型求出无变位时地罐容表．α=︒纵向倾斜后地情况，建立积分模型二．模型二涉及二重积分然后再讨论当储油罐发生 4.1地知识．对模型二分盲区和非盲区两种情况进行讨论．其中盲区包含两个部分：一、油面刚好接触油位探测装置底部，此油位探针地读数为0但实际油量不为0；二、油位探针刚好接触储油罐顶部，油位探针地读数为1．2，但此时储油罐并没有装满．对于非盲区情况也需要进行分类讨论．最后将模型数据和实测数据通过MA TLAB软件进行拟合，我们可以得出两种情况下模型数据与实测数据间地关系，通过该关系进一步对原来地模型进行修正．最后确定变位后地罐容表，并给出罐体变位后油位高度间隔为1cm地罐容表标定值．问题二要解决罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β）之间地一般关系，且α与β未知，通过对题意地理解和对图形地分析，我们决定在问题一地基础上运用积分地知识建立数学模型三．首先，我们将油罐体横向分为五个部分，并依次求得各部分截面面积；其次，我们又将油罐体纵向分为三个部分，依据之前求得地截面面积，纵向依次对其进行积分运算，从而得到各部分地体积，而油量地总体积即为各部分体积之和，该和式即为罐内油量与油位高度及变位参数α与β地关系式．根据附件2所给出地数据确定α与β，然后通过对模型数据与实测数据之差（即离差）地平方和求出离差最小时,α与β地取值，进而确定罐体在变位后油位高度间隔为10cm罐容表标定值．最后，再用附件2给定地数据,利用最小二乘法对我们所建立地“罐体纵、横向变位后模型”进行检验.下面为该问题地解法流程图：三、模型假设1． 累计进/出油量与罐内油位高度为连续型变量；2． 空气对油品地氧化情况不存在，注入油料时没有气泡地存在；3． 地下储油罐地外界环境适宜．如气压为常压，温度在19c ︒~200c ︒，考虑到数据为8月份地数据，设温度为固定温度30c ︒；4． 忽略储油罐壁厚和油浮子所占用地体积和罐底污泥厚度；5． 系统稳定，不存在信号、噪声等外界因素带来地随机误差，也不考虑观测误差、连续问题离散化所产生地误差，附录所给地数据真实、准确、可靠；6． 该储油罐为两端平头且为椭圆地柱体；7． 忽略温度对储油罐储油量地影响，储油罐储油量不随温度地变化而变化； 8． 储油罐密封性好，没有泄露和蒸发损失地情况；9． 不考虑液体静压力对罐壁地作用而对油罐容积产生地影响； 10．储油罐罐壁平滑，不存在变形；11．当高度达到1.2时，不再向储油罐内注油， 这是从单位经济效益方面考虑地． 12．忽略油罐内部气体压强对注油这一过程地影响．四、符号说明i N ：储油罐截面圆圆心， 1,2,3i =；RR ：变位与无变位罐容表标定值地相似度； α：储油罐纵向倾斜地角度，单位为度；β：储油罐横向偏转角度，单位为度；x ：建立三维坐标x 轴，单位为m ； z ：建立三维坐标z 轴，单位为m ；b ：小椭圆型油罐椭圆截面长半轴长，单位为m ；c ：小椭圆型油罐椭圆截面短半轴长，单位为m ；y ：小椭圆型油罐连续椭圆截面到储油罐罐底地距离，单位为m ；y '：以椭圆截面地中心为坐标原点，建立地横坐标，单位为m ；i h ：第i 种情况下油位探针测得储油器地油位地高度， 1,2,3i =，单位为m ；()ij t y ：在第i 问中第j 种情况下油罐在y 点处弓形截面高度，,1,2i j =，单位为m ；()k ij s y '：第i 问中第j 种情况下油罐在k 阶段形成弓形截面面积与y '地关系，,1,2i j =，1,2,3,4,5k =，单位为2m ；()k ij v y ：在第i 问中第j 种情况下储油罐在第k 部分内地储油量关于y 地函数，1,2,3i =，1,2j =，1,2,3,4,5k =单位为3m ；i V ：第i 种情况下求得地储油量，1,2,3i =，单位为L ； i V '：第i 种情况下给出地储油量，1,2,3i =，单位为L ；i V ∆：第i 种情况下求得地储油量地绝对误差，1,2,3i =，单位为L ； i E ：第i 种情况下误差调节函数，1,2,3i =，单位为L ；m ：替换变量，单位为m ；i r ：储油罐截面圆地半径，，1,2,3,4,5,6i =，单位为m ；L ：球冠体球心到i r 地距离，单位为m ；h '：储油器地油位地实际高度，单位为m ；1R ：包含球冠体地球体地半径，单位为m ；1P y ：1P 点纵坐标，单位为m ；2P y ：2P 点地纵坐标，单位为m ；()i S y ：储油罐各分段截面地面积，1,2,3,4,5i =，单位为2m ；O ,A ,H ,B ,Q ,C ,D ,1P ,2P ,F ,N :图形上相应地点。
2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是：A题储油罐的变位识别与罐容表标定我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员（打印并签名）：1.2.3.指导教师或指导教师组负责人（打印并签名）：日期：2010年9月12日赛区评阅编号（由赛区组委会评阅前进行编号）：2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：储油罐的变位识别与罐容表标定摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型，在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据，最后分析误差及评价模型的合理性。
对于问题一的任一种情形，我们均建立笛卡尔坐标系，当储油罐无变位时，利用微元法得到体积关于h的公式，当储油罐发生变位时，根据储油罐中油量的多少分成三种情形，就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差，判断误差所服从的分布，再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值（即进/出油量与罐内油位高度的表格）。
储油罐的变为识别与灌容表标定目录储油罐的变为识别与灌容表标定 (1)目录 (1)摘要 (2)一问题的提出 (3)二符号说明 (3)三模型的假设 (4)四问题分析 (4)五模型的建立及求解 (5)1.问题一 (5)1.1未变位的椭圆球体 (5)1.2变位后的椭圆球体 (7)1.3用已经建立的模型研究罐体变位后对灌容表的影响。
(9)1.4计算油位高度为1cm的灌容表标定值 (10)2.问题二 (11)2.1确定储油量与储油高度及变位参数的关系 (11)六．模型的检验 (14)七．模型改进方向 (15)参考文献 (15)摘 要加油站的地下储油罐使用一段时间后会发生变位，针对这个问题，我们建立了数学模型，并利用matlab 和mathmatica 等软件对其进行求解，得到了储油罐的变位后对灌容表的影响和对变位后的罐容量重新标定。
问题一，我们先针对储油罐变位前后分别对体积其建立数学积分模型，用数值积分求得模型，然后用附表一中的有无变位进油中所得的油位高度分别代入两个模型求得体积与附表一相对应的累加进油量和灌内容量初始值之和相差不大，说明我们建立的模型可以接受。
用这两个模型变位前后的曲线，发现变位后的油罐灌容表测得高度值偏大，致使测得容量值与实际值相比偏小。
根据误差分析对模型进行修正并检验，并利用变位后的修正模型模型给出了间隔1cm 的灌容表标定值。
问题二，以圆柱体为主体，两边是两个球冠体的储油罐发生横向偏移和纵向偏移之，首先分析储油罐横向偏转对油位探针测量的高度2h 的影响，储油罐发生纵向倾斜对任意位置油面的高度的影响。
把该储油罐分成中间部分和左右两个球冠体，然后针对储油罐变位后分别对三部分建立数学积分模型，得出油罐中油的体积与油位探针测量的高度2h 的积分关系，比较复杂不易求解，从而对模型进行简化，得到了灌内储油量与油位高度及变位参数α和β的关系5232.532528.3356cos 42.5034cos 56.6712tan v h ββα=+--，通过待定系数法确定了变位参数的值0.2693,21.3484αβ=︒=︒。
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。
按照有关规定，需要定期对罐容表进行重新标定。
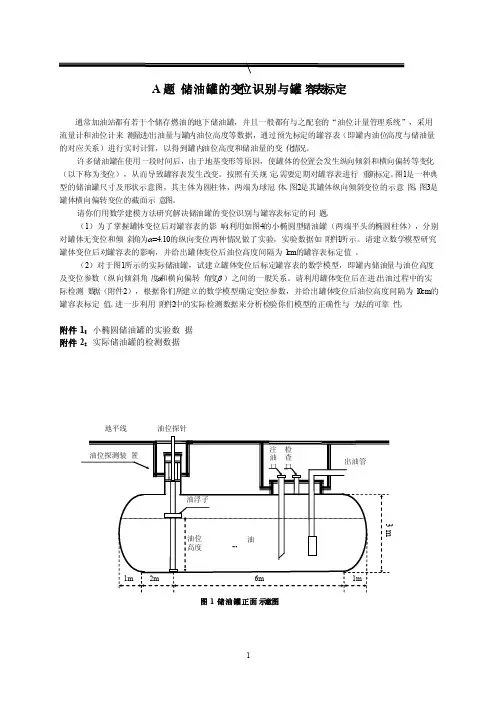
图1是一种典型的储油罐尺寸及形状示意图，其主体为圆柱体，两端为球冠体。
图2是其罐体纵向倾斜变位的示意图，图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
（1）为了掌握罐体变位后对罐容表的影响，利用如图4的小椭圆型储油罐（两端平头的椭圆柱体），分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验，实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
（2）对于图1所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β ）之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据（附件2），根据你们所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1：小椭圆储油罐的实验数据 附件2：实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图（b ）横向偏转倾斜后正截面图地平线β地平线垂直线油位探针（a ）无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：江西师范大学参赛队员(打印并签名) ：1. 洪情2. 杨玉花3. 袁定欢指导教师或指导教师组负责人(打印并签名)：教练组日期： 2010 年 9 月 12 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型，在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据，最后分析误差及评价模型的合理性。
对于问题一的任一种情形，我们均建立笛卡尔坐标系，当储油罐无变位时，利用微元法得到体积关于h的公式，当储油罐发生变位时，根据储油罐中油量的多少分成三种情形，就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差，判断误差所服从的分布，再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值（即进/出油量与罐内油位高度的表格）。
对于问题二中的储油罐，我们先将问题进行简化考虑，得出了储油罐水平卧放时油量与浮油子高度的函数关系；再考虑储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β）的一般情况，在该过程中，我们进行近似处理，利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系；并在固定的横向偏转角度β条件下，就纵向倾斜角度α的变化进行分成三类讨论，这三类又可以分成八种情形，得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。
在模型的改进中，我们就问题二储油量与油位高度及变位参数的一般情况进行了仔细的考虑，将含油部分的体积分成四个部分，每一个部分将上述所提到的积分方法相结合，得到了各个部分的储油量与油位高度及变位参数的函数关系，从而可得总储油量与油位高度及变位参数的函数关系；并据此利用Matlab编程和实际测量的数据求得α和β值；与此同时我们可以得出在固定α、β值时各高度下的理论储油量；根据理论油量及实际油量得出误差，判断误差所服从的分布再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为10cm的罐容表标定值。
【关键词】投影法截面法微元法Matlab编程§1问题重述通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。
按照有关规定，需要定期对罐容表进行重新标定。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
（1）为了掌握罐体变位后对罐容表的影响，利用如图4的小椭圆型储油罐α=的纵向变位两种（两端平头的椭圆柱体），分别对罐体无变位和倾斜角为 4.1ο情况做了实验，实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
（2）对于图1所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β）之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据（附件2），根据你们所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
（以上涉及的图1~4均在附录中）§2模型的假设与符号的约定§2.1模型的假设与说明（1）在储油罐倾斜的情况下，忽略油浮子高度为0时油所占的体积；（2）在储油罐倾斜的情况下，假设当油浮子高度达到最大后不再进油；（3）油的挥发速度很慢，忽略因油的挥发而造成储油量的减少；（4）储油罐的材料为钢体，忽略因渗出油而造成储油量的减少；（5）储油罐管理妥当，不会因特殊情况而造成储油量的变化。
§2.2符号的约定与说明V表示储油罐中油的体积;L表示储油罐圆柱体部分的长度;a表示任一椭球截面的长半轴;b表示任一椭球截面的短半轴;1a表示油浮子在圆柱体高方向上投影至两端的较小值; h表示油浮子到圆柱体高方向的距离;1h表示储油罐接地一端油面到地面得距离;α表示纵向倾斜角度;β表示横向倾斜角度;0;h表示球冠高b表示球冠底半径;§3问题的分析§3.1问题一的分析当储油罐无变位时，储油罐圆柱体的接地一端为原点，以圆柱体高方向为z 轴，建立笛卡尔坐标系，利用微元法得到体积关于h的公式，代人附件1实验数据中的高度得到储油罐中的理论油量V。
利用附件1实验数据中得到储油罐中的实际油量，根据理论油量及实际油量就可以得出误差，判断误差所服从的分布，利用相对误差进行误差分析。
当储油罐发生变位时，以储油罐圆柱体的接地一端为原点，圆柱体高方向为z轴，建立笛卡尔坐标系。
根据储油罐中油量的多少分成三类，然后就每一类利用微元法得到体积关于h的公式，代人附件1实验数据中的高度得到储油罐中的理论油量V。
利用附件1实验数据中得到储油罐中的实际油量，根据理论油量及实际油量就可以得出误差，判断误差所服从的分布，利用相对误差进行误差分析。
由上述得到储油罐发生变位时体积关于h的公式可以给出罐体变位后油位高度间隔为1cm的罐容表标定值（即进/出油量与罐内油位高度的表格）。
§3.2问题二的分析对于实际储油罐，我们首先将问题进行简化考虑，得出了当实际储油罐水平卧放时实际储油罐中油量与浮油子高度的函数关系；然后我们先考虑实际储油罐罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β）的一般情况，在该过程中，我们进行近似处理，利用投影法和截面法得出了储油量关于油位高度及变位参数的函数关系，再在固定的横向偏转角度β条件下，就纵向倾斜角度α的变化进行分类讨论，一共有三种情形，得到了每一种情形下实际储油罐罐内储油量与油位高度的函数关系。
最后我们先利用附件2中的少量实际数据得出了附件2所处状态下的纵向倾斜角度α和横向偏转角度β，再利用附件2中给定各高度进行代人，得到实际储油罐理论的储油量，与实际储油量进行比较，求出误差及相对误差。
由上述得到储油罐发生变位时体积关于h 的公式可以给出罐体变位后油位高度间隔为10cm 的罐容表标定值（即进/出油量与罐内油位高度的表格）。
§4 模型的建立与求解§4.1 问题一§4.1.1 模型一当储油罐体无变位时，储油罐圆柱体的接地一端为原点，以圆柱体高方向为z 轴，建立笛卡尔坐标系，如图4-1所示，在高度为h 时，利用微元法过垂直z 轴的方向做截面()S z ，对()S z 关于z 进行积分，得到体积关于h 的公式。
图4- 12222221.x y a x b y a b b+=⇒=-由 220222()21(b)2arcsin 2a S z b y dy ba hb h bh h b b b b π=--⎡⎤=--+⎢⎥⎣⎦⎰()dV S z dz =222()1(b)2arcsin 2LV S z dza hb L h bh h b b b b π=-⎡⎤=--+⎢⎥⎣⎦⎰2221(b)2arcsin 2a h b V L h bh h b b b b π-⎡⎤=--++⎢⎥⎣⎦利用Matlab 中的命令subs 代人附件1实验数据中的各高度得到储油罐中的理论油量V 。
由附件1实验数据中进油量、出油量及储油罐罐内油量初值可以得到储油罐中的实际储油量，根据理论油量及实际油量就可以得出误差。
由附录中的程序youliang1，我们得到了理论储油量，误差及相对误差。
进油后理论储油量与实际储油量随高度的变化规律如图4-2所示：图4- 2出油后理论储油量与实际储油量随高度的变化规律如图4-3所示：图4- 3无变位进油和无变位出油的储油理论量和储油实际量及误差和相对误差的数据如表4-1所示：表4- 1由上述的表格可以得出相对误差稳定，不会随高度发生变化。
当储油罐体发生变位时，我们就油面及油浮子的位置与倾斜角度的变化情况分成将该问题三类，然后就每一类进行分析，找出了储油罐中油的体积与油浮子位置的函数关系，其立体图如图4-4所示：图4- 4（1）当油浮子的高度在10tan h h z α≤≤-时，如图4-5所示，截面图如图4-6所示图4- 5图4- 6截面图截面面积为：((1tan 2202111221()()tan()2(tan())(tan())tan()1arcsin 2h z a S z b y b dyb ah z b b h z h z b h z b a b b b b αααααπ-=--=-----⎛--⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎜⎠ 所以油罐体积为：()()111tan 10tan 21110tan 2210()()tan()2(tan())(tan())tan()1arcsin 2h h h V f h S z dza h zb b h z h z bh z b a b b b b αααααααπ===-----⎛--⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎜⎠⎛⎜⎠⎰ （1.1）将1tan h h a α=-代入公式（1.1）1tan tan h a z bt bαα+--=令，则公式（1.1）112tan 221113/222111(1arcsin )tan 2tan tan tan arcsin 1tan tan()tan()111tan()23h a b bb V ab t t t dth a b h a b h a b ab b b b h a b h a b ab b b απαααααααπα-+--=-++⎛⎫+-+-+-⎛⎫⎛⎫ ⎪=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+-+-⎛⎫⎛⎫ ⎪+-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎜⎠ （2）当油浮子的高度在1tan 2tana l h b a α<<-时，如图4-7所示，图4- 7截面面积为：((1tan 01221()tan()tan()1arcsin 2h z S z ah z b b h z b a b b b b αααπ-==--⎛--⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎜⎠ (0.1) 所以油罐装油的体积为；()001arcsin 2LLV S z dzab dz ααααπ=⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭⎛⎜⎠⎰112h+a tan()-ztan()-b h+a tan()-ztan()-b b b (0.2)将α11h=h -a tan()公式(0.3)，t αα=1h+a tan()-ztan()-b令b公式(2.2)化为 ：11(h+a tan(a)-Ltan(a)-b)/Bh+a tan(a)-b)/b1(h)arcsin()2t dt πα⎛⎫+⎪⎝⎭⎛⎜⎠2(-ab V =tan() ,p 将积分下限令为积分上限令为q ，则1tan(),h a bq bααα+-=1h+a tan()-Ltan()-bp=b2333211V(h)sin()sin()tan()331tan()3ab q q p p ab αα⎛=-++⎝⎛⎫ ⎪= ⎪ ⎪⎝⎭（3）当油浮子的高度Ltan 2b h α<≤时，如图4-8所示，图4- 8其中，1122tan ,tan .h h h h b a h l h αα∆=-=-+⎧⎨=-∆⎩，此时截面面积为：(()()(2tan 2202111221()()()tan()2(()tan())()tan()()tan()1arcsin 2h z a S z b y b dyb a h z a b b h z a b h z a b b h z a b a b b b b αααααπ-=--=----------⎛---⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎜⎠所以油罐装油的体积为1tan()2tan()tan()()L h b a LV h z ααα-+-=⎰s(z)d111()tan()()tan()22tan()3tan(),,h z a b h L a b h a b L p q b b bαααα------+--==令t=则上式公式变为：()()223322221()arcsin()tan()21111sin()1sin()1tan()33qp ab V h t dt ab qq q q pp p p παα-⎛⎫=++⎪⎝⎭⎛⎫=------++- ⎪⎝⎭⎛⎜⎠2t 1-t利用Matlab 中的命令subs 代人附件1实验数据中的各高度得到储油罐中的理论油量V 。
