中考数学几何中的类比探究综合测试卷

1.如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．（1）求∠CAE的度数；（2）取AB边的中点F，连接CF、CE，试证明四边形AFCE是矩形．2.如图①，在△ABC中,AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点, ED 为一边，作∠DEF=∠A，另一边EF交AC于点F.(1)求证:四边形ADEF为平行四边形；(2)当点D为AB中点时，▱ADEF的形状为；(3)延长图①中的DE到点G, 使EＧ＝DE，连接AE,AG,FG得到图②若AD =AG, 判断四边形AEGF的形状，并说明理由.3.【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．【探究展示】（1）证明：AM=AD+MC；（2）AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．【拓展延伸】（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．4,在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．（1）观察猜想：如图1，当点D在线段BC上时，①BC与CF的位置关系为：．②BC，CD，CF之间的数量关系为；（2）数学思考：如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）拓展延伸如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2√2，BC，请求出GE的长．CD=145.如图，四边形ABCD 是边长为2，一个锐角等于60°的菱形纸片，将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点 D 重合，按顺时针方向旋转这个三角形纸片，使它的两边分别交CB，BA（或它们的延长线）于点E，F；①当CE=AF 时，如图①，DE 与DF 的数量关系是；②继续旋转三角形纸片，当CE≠AF 时，如图②，（1）的结论是否成立？若成立，加以证明；若不成立，请说明理由；③再次旋转三角形纸片，当点E，F 分别在CB，BA 的延长线上时，如图③，请直接写出DE 与DF 的数量关系．6.（1）问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系.小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论.（2）（类比引申）如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足________关系时，仍有EF=BE+FD.（3）（探究应用）如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD.已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（√3﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，√2=1.41，√3=1.73）7.在菱形ABCD 中，∠ ABC=60° ，点P 是射线BD 上一动点，以AP 为边向右侧作等边△ APE ，点E 的位置随着点P 的位置变化而变化．（ 1 ）如图1 ，当点 E 在菱形ABCD 内部或边上时，连接CE ，BP 与CE 的数量关系是，CE 与AD 的位置关系是；（ 2 ）当点E 在菱形ABCD 外部时，（ 1 ）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（选择图 2 ，图3 中的一种情况予以证明或说理）；（ 3 ）如图4 ，当点P 在线段BD 的延长线上时，连接BE ，若AB=2 ，BE=2 ，求四边形ADPE 的面积8,如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PB=PE，连接PD，O为AC 中点．（1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；（2）如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由；（3）如图3，当点P在AC的延长线上时，请你在图3中画出相应的图形（尺规作图，保留作图痕迹，不写作法），并判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．。

类比探究综合测试（通用版）试卷简介:测试学生在处理类比探究问题过程中，有没有类比照搬的意识，能否根据题干或者问与问之间的联系，照搬辅助线，照搬思路来解决问题，同时考查学生对于类比探究中中点结构、旋转结构、平行结构这三种特殊结构的处理思路。

一、单选题(共6道，每道16分)1.如图1，△ABC和△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，点D在AB边上．连接EC，取EC的中点F，连接AF，DF．为了证明AF⊥DF，AF=DF，我们只需要延长DF交线段AC于点G，说明AF是等腰直角三角形ADG的中线即可．现将△BDE旋转至如图2所示的位置，使点E在AB的延长线上，点D在CB的延长线上，其他条件不变，类比上面的做法，为了证明AF⊥DF，AF=DF，我们需要作的辅助线是( )A.连接ADB.过点C作CG⊥DF，交DF的延长线于点GC.延长DF交AC的延长于点G，连接ADD.延长DF到G，使DF=FG，连接CG，AD，AG答案：D解题思路：在图1中，给出的辅助线达到的一个效果就是保证F是等腰直角三角形ADG斜边的中点，满足DF=FG．若在图2中达到同样的效果，需要延长DF到G，使DF=FG，这样再连接AD，AG之后才能保证F是等腰直角三角形ADG斜边的中点．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）在试题1图2的证明中，说明△ADG是等腰直角三角形之前，证明AD=AG 需要直接使用到某对三角形全等，则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案：D解题思路：要证明AD=AG，我们需要证明△ABD≌△ACG．根据上一题的分析，如图，延长DF到G，使DF=FG，连接CG，AD，AG，容易证明△DEF≌△GCF，∴CG=ED=BD，∠DEF=∠GCF，∴DE∥CG，∴∠GCD=∠BDE=90°，∴∠GCA=∠DBA=135°．又∵AC=AB，∴△ABD≌△ACG（SAS）．（为了证明AF⊥DF，AF=DF，接下来需要根据得出的条件，说明∠DAG=90°，进而说明AF是等腰直角三角形ADG斜边上的中线）试题难度：三颗星知识点：中考数学几何中的类比探究3.如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF．利用旋转的思想很容易证明DE+BF=EF；如图2，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且．则DE，BF，EF之间的数量关系为( )A. B.C.DE+2BF=EFD.DE+BF=EF答案：D解题思路：在图1中，旋转思想考虑了两个方面，一个是AB=AD，能够实现旋转，一个是，能够将角度放在一起，所以图1中的证明是将△DAE旋转，使得AD 与AB重合，这是一种思想，作辅助线的时候是延长CB到点G，使得BG=DE，最后证明GF=EF．图2中有同样的两个结构：AB=AD，，所以照搬分析图1的思路来研究数量关系．如图，延长CB到点G，使得BG=DE，连接AG．易证△ADE≌△ABG，∴AE=AG，BG=DE，∠DAE=∠BAG，∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF．∵，∴∠GAF=∠EAF．又∵AF=AF，∴△GAF≌△EAF，∴GF=EF，∴EF=GB+BF=DE+BF，即DE，BF，EF满足的数量关系是DE+BF=EF．试题难度：三颗星知识点：类比探究问题4.（上接第3题）如图3，在四边形ABCD中，AB=AD，E，F分别为DC，BC边上的点，且满足，当∠ABC与∠ADC满足( )时，可使得DE+BF=EF．A.∠ABC=∠ADCB.∠ABC+∠ADC=180°C.∠ABC=2∠ADC-180°D.∠ABC+2∠ADC=270°答案：B解题思路：试题3中图1和图2的证明，都是利用旋转的思想来证明DE+BF=EF，从作辅助线开始到结束，整个分析有以下几点：延长CB到点G，使得BG=DE，证明△ABG≌△ADE（SAS），导出∠GAF=∠EAF，进而证明△GAF≌△EAF（SAS），之后导出线段关系．若在图3中用此方法证明，首先延长CB到点G，使得BG=DE，要证明△ABG和△ADE全等，需要保证∠ABG=∠ADE，也就是需要∠ABC+∠ADC=180°，所以需要添加的条件是∠ABC+∠ADC=180°．添加条件之后的证明如下：如图，延长CB到点G，使得BG=DE，连接AG．∵∠ABC+∠ADC=180°，∠ABC+∠ABG=180°，∴∠ABG=∠ADE．又∵AB=AD，BG=DE，∴△ADE≌△ABG，∴AE=AG，BG=DE，∠DAE=∠BAG，∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF．∵，∴∠GAF=∠EAF．又∵AF=AF，∴GF=EF，∴EF=GB+BF=DE+BF．试题难度：三颗星知识点：类比探究问题5.如图，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．若BD=2CD，CF=mAF，则的值是( )A. B.C. D.答案：B解题思路：如图，过点D作DG∥AC，交AB于点G．设CD=a，BD=2a，AF=b，CF=mb．∵△BDG∽△BCA，∴∴，BG=2AG．设AG=c，BG=2c，∴，即∴∴试题难度：三颗星知识点：中考数学几何中的类比探究6.如图，D是△ABC的边BC上一点，过点D的一条直线交AC的延长线于点F，交AB于点E．若BD=aCD，CF=bAF，则的值是( )A. B.C. D.答案：D解题思路：如图，过点D作DG∥AC，交AB于点G．设CD=m，BD=am，AF=n，CF=bn．∵△BDG∽△BCA，∴∴，BG=aAG．设AG=c，BG=ac，∵△EAF∽△EGD，∴，即∴∴．试题难度：三颗星知识点：中考数学几何中的类比探究。

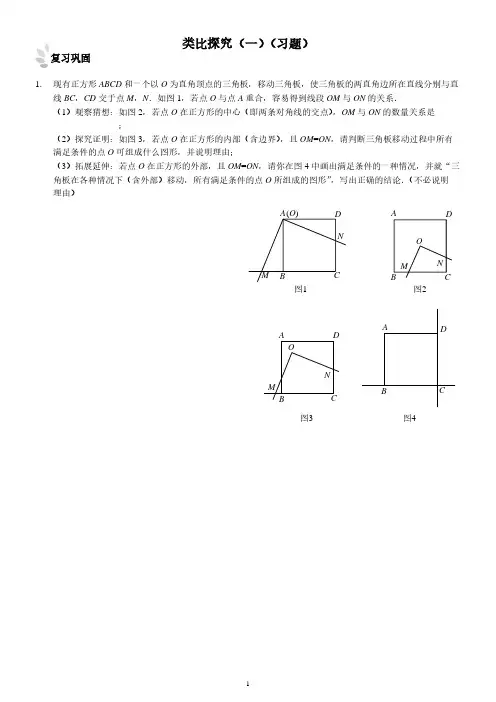
类比探究（一）（习题）1. 现有正方形ABCD 和一个以O 为直角顶点的三角板，移动三角板，使三角板的两直角边所在直线分别与直线BC ，CD 交于点M ，N ．如图1，若点O 与点A 重合，容易得到线段OM 与ON 的关系． （1）观察猜想：如图2，若点O 在正方形的中心（即两条对角线的交点），OM 与ON 的数量关系是_______________；（2）探究证明：如图3，若点O 在正方形的内部（含边界），且OM =ON ，请判断三角板移动过程中所有满足条件的点O 可组成什么图形，并说明理由；（3）拓展延伸：若点O 在正方形的外部，且OM =ON ，请你在图4中画出满足条件的一种情况，并就“三角板在各种情况下（含外部）移动，所有满足条件的点O 所组成的图形”，写出正确的结论．（不必说明 理由）图1A BCD M (O )NNO M DCBA图2NOM DCBA 图3ABCD图4复习巩固2. （1）问题发现：如图1，在等边△ABC 中，点D 为BC 边上一动点，DE ∥AB 交AC 于点E ，将AD 绕点D 顺时针旋转60°得到DF ，连接CF ．则AE 与FC 的数量关系是_________，∠ACF 的度数为________． （2）拓展探究：如图2，在Rt △ABC 中，∠ABC =90°，∠ACB =60°，点D 为BC 边上一动点，DE ∥AB 交AC 于点E ，当∠ADF =∠ACF =90°时，求AEFC的值． （3）解决问题：如图3，在△ABC 中，BC :AB =m ，点D 为BC 的延长线上一点，过点D 作DE ∥AB 交AC 的延长线于点E ，直接写出当∠ADF =∠ACF =∠ABC 时，AEFC的值．3. 如图，在Rt △ABC 中，AC =BC =4，∠ACB =90°，正方形BDEF 的边长为2，将正方形BDEF 绕点B 旋转一周，连接AE ，BE ，CD ． （1）猜想：CDAE的值是___________，直线CD 与直线AE 相交所成的锐角度数是_____________． （2）探究：直线DE 与AF 垂直时，求线段CD 的长；（3）拓展：取AE 的中点M ，连接FM ，直接写出线段FM 长的取值范围．图1ABCD EF图2AB CD EF图3AB CDE F图1FEDCBA图2A B C图3ABC【参考答案】1. （1）OM =ON ；（2）三角板移动过程中所有满足条件的点O 可组成对角线AC ，理由略；（3）图略；三角板在各种情况下（含外部）移动，所有满足条件的点O 所组成的图形是直线AC 或过点C 且与直线AC 垂直的直线． 2. （1）AE =FC ；60°；（2）AEFC = （3）1AE FC m=．3. （1）2；45°；（2）CD ；（3FM ≤。

2017中考第22题类比探索题专题一例1.1问题发现如图1;△ACB和△DCE均为等边三角形;点A、D、E在同一直线上;连接BE填空：1∠AEB的度数为；2线段BE之间的数量关系是 ..2拓展探究如图2;△ACB和△DCE均为等边三角形;∠ACB=∠DCE=900; 点A、D、E在同一直线上;CM为△DCE中DE边上的高;连接BE..请判断∠AEB的度数及线段CM、AE、BE之间的数量关系;并说明理由..3解决问题如图3;在正方形ABCD中若点P满足PD=1;且∠BPD=900;请直接写出点A到BP的距离..例2.如图1;将两个完全相同的三角形纸片ABC和DEC重合放置;其中∠C=90°;∠B=∠E=30°.1操作发现如图2;固定△ABC;使△DEC绕点C旋转;当点D恰好落在AB边上时;填空：①线段DE与AC的位置关系是_________；②设△BDC的面积为S1;△AEC的面积为S2;则S1与S2的数量关系是_________________.2猜想论证当△DEC 绕点C 旋转到图3所示的位置时;小明猜想1中S 1与S 2的数量关系仍然成立;并尝试分别作出了△BDC 和△AEC 中BC 、CE 边上的高;3拓展探究已知∠ABC =60°交BC 于点E 如图4. 若在射线BA 上存在点F ;使S △DCF =S △BDE ;请直接写出．．．．相应的BF 的长. 专题训练1.等腰△PAB 中; ∠PAB=900;点C 是AB 上一点与A 、B 不重合;连接PC;将线段PC 绕点C 顺时针旋转900;得到线段DC;连接PD 、BD.探究∠PBD 的度数;以及线段AB 及BD 、BC 的数量关系.⑴尝试探究：如图点C 在线段AB 上;可通过证明△PAC ∽△PBD;得出结论：∠PBD= ；AB= 不需要证明⑵类比探索：点C 在直线AB 上;且在点B 右侧;还能得出与⑴相同的结论吗 请写出你得出的结论并证明;⑶拓展迁移: 点C 在直线AB 上;且在点A 左侧;请补充完成图形;并直接写出得到的结论.2.如图①;正方形AEFG 的边长为1;正方形ABCD 的边长为3;且点F 在AD 上. ⑴求△DBF 的面积;AD BEC图1AC图2图3EE CB 图4⑵把正方形AEFG绕点A逆时针方向旋转450;得到图②;求图②中的△DBF的面积;⑶把正方形AEFG绕点A旋转一周;在旋转过程中; △DBF存在最大值与最小值;请直接写出最大值 ;最小值3.提出问题1如图1;在等边△ABC中;点M是BC上的任意一点不含端点B、C;连结AM;以AM为边作等边△AMN;连结CN．求证：∠ABC=∠ACN．类比探究2如图2;在等边△ABC中;点M是BC延长线上的任意一点不含端点C;其它条件不变;1中结论∠ABC=∠ACN还成立吗请说明理由．拓展延伸3在等腰△ABC中;BA=BC;点M是BC上的任意一点不含点B、C;连结AM;以AM为边作等腰△AMN;使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系;并说明理由．4.某数学兴趣小组开展了一次课外活动;过程如下：如图1;正方形ABCD中;AB=6;将三角板放在正方形ABCD上;使三角板的直角顶点与D点重合．三角板的一边交AB于点P;另一边交BC的延长线于点Q．1求证：DP=DQ；2如图2;小明在图1的基础上作∠PDQ的平分线DE交BC于点E;连接PE;他发现PE和QE存在一定的数量关系;请猜测他的结论并予以证明；3如图3;固定三角板直角顶点在D点不动;转动三角板;使三角板的一边交AB的延长线于点P;另一边交BC的延长线于点Q;仍作∠PDQ的平分线DE交BC延长线于点E;连接PE;若AB：AP=3：4;请帮小明算出△DEP的面积．5.已知两个共一个顶点的等腰Rt△ABC;Rt△CEF;∠ABC=∠CEF=90°;连接AF;M是AF的中点;连接MB、ME．1如图1;当CB与CE在同一直线上时;求证：MB∥CF；2如图1;若CB=a;CE=2a;求BM;ME的长；3如图2;当∠BCE=45°时;求证：BM=ME．6.有一副直角三角板;∠BAC=90°;AB=AC=6;在三角板DEF中;∠FDE=90°;DF=4;DE=．将这副直角三角板按如图1所示位置摆放;点B与点F重合;直角边BA与FD在同一条直线上．现固定三角板ABC;将三角板DEF沿射线BA方向平行移动;当点F运动到点A时停止运动．1如图2;当三角板DEF运动到点D到点A重合时;设EF与BC交于点M;则∠EMC= 度；2如图3;当三角板DEF运动过程中;当EF经过点C时;求FC的长；3在三角板DEF运动过程中;设BF=x;两块三角板重叠部分的面积为y;求y与x的函数解析式;并求出对应的x取值范围．7.已知四边形ABCD中;E、F分别是AB、AD边上的点;DE与CF交于点G．（第25题图）图3图2图1FEPCBDAFEPDCBAFEPDCBA1如图①;若四边形ABCD 是矩形;且DE ⊥CF;求证CDADCF DE =； 2如图②;若四边形ABCD 是平行四边形;试探究：当∠B 与∠EGC 满足什么关系时;使得CDADCF DE =成立 并证明你的结论； 3如图③;若BA =BC =6;DA =DC =8;∠BAD ＝90°;DE ⊥CF ;请直接写出CFDE的值． 8.如图;矩形ABCD 中;∠ACB =o 30;将一块直角三角板的直角顶点P 放在两对角线AC ;BD 的交点处;以点P 为旋转中心转动三角板;三角板的两直角边分别于边AB ;BC 所在的直线交于E ;F .1当PE ⊥AB ;PF ⊥BC 时;如图1;则PEPF的值为 . 2现将三角板绕点P 逆时针旋转αo o 060α<<角;如图2;求PEPF的值； 3在2的基础上继续旋转;当o o 6090α<<;且使AP :PC =1：2时;如图3;PEPF的值是否变化 证明你的结论.操作体验用一张矩形纸片折等边三角形． 第一步;对折矩形纸片ABCDAB ＞BC 图①;使AB 与DC 重合;得到折痕EF ;把纸片展平图②．第二步;如图③;再一次折叠纸片;使点C 落在EF 上的P 处;并使折痕经过点B ;得到折痕BG ;折出PB ;PC ;得到△PB C ． 1说明△PBC 是等边三角形． 数学思考2如图④．小明画出了图③的矩形ABCD 和等边三角形PB C ．他发现;在矩形ABCD 中把△PBC 经过图形变化;可以得到图⑤中的更大的等边三角形．请描述图形变第24题图③ABCDF GE化的过程．3已知矩形一边长为3cm ;另一边长为acm ．对于每一个确定的a 的值;在矩形中都能画出最大的等边三角形．请画出不同情形的示意图;并写出对应的a 的取值范围． 问题解决4用一张正方形铁片剪一个直角边长分别为4cm 和1cm 的直角三角形铁片;所需正方形铁片的边长的最小值为 cm ．如图1;点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上;AE ＝DG ;求证：2S 四边形EFGH ＝S 矩形ABCD ．S 表示面积实验探究：某数学实验小组发现：若图1中AH ≠BF ;点G 在CD 上移动时;上述结论会发生变化;分别过点E 、G 作BC 边的平行线;再分别过点F 、H 作AB 边的平行线;四条平行线分别相交于点A 1、B 1、C 1、D 1;得到矩形A 1B 1C 1D 1．如图2;当AH ＞BF 时;若将点G 向点C 靠近DG ＞AE ;经过探索;发现：2S 四边形EFGH ＝S矩形ABCD＋1111A B C D S 矩形．如图3;当AH ＞BF 时;若将点G 向点D 靠近DG ＜AE ;请探索S四边形EFGH、S矩形ABCD与1111A B C D S 矩形之间的数量关系;并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题：1如图4;点E 、F 、G 、H 分别是面积为25的正方形ABCD 各边上的点;已知AH ＞BF ;AE ＞DG ;S四边形EFGH ＝11;HF 求EG 的长．2如图5;在矩形ABCD 中;AB ＝3;AD ＝5;点E 、H 分别在边AB 、AD 上;BE ＝1;DH ＝2;点F、G分别是边BC、CD上的动点;且FG连接EF、HG;请直接写出四边形EFGH面积的最大值．点E在边CD上移动;连接AE;将如图;在矩形纸片ABCD中;已知AB＝1;BC多边形ABCE沿直线AE翻折;得到多边形AB′C′E;点B、C的对应点分别为点B′、C′．1当B′C′恰好经过点D时如图1;求线段CE的长；2若B′C′分别交边AD;CD于点F;G;且∠DAE＝22.5°如图2;求△DFG的面积；3在点E从点C移动到点D的过程中;求点C′运动的路径长．如图;已知正方形ABCD的边长为4;点P是AB边上的一个动点;连接CP;过点P 作PC的垂线交AD于点E;以PE为边作正方形PEFG;顶点G在线段PC上;对角线EG、PF相交于点O．1若AP=1;则AE= ；2①求证：点O一定在△APE的外接圆上；②当点P从点A运动到点B时;点O也随之运动;求点O经过的路径长；3在点P从点A到点B的运动过程中;△APE的外接圆的圆心也随之运动;求该圆心到AB边的距离的最大值．如图1;△ABC中;∠B=30°;AB=3;BC=4;则△ABC的面积等于．探究图2是同学们熟悉的一副三角尺;一个含有30°的角;较短的直角边长为a；另一个含有45°的角;直角边长为b;小明用两副这样的三角尺拼成一个平行四边形ABCD如图3;用了两种不同的方法计算它的面积;从而推出sin;小丽用两副这样的三角尺拼成了一个矩形EFGH如图4;也推出sin;请你写出小明或小丽推出sin的具体说理过程．应用在四边形ABCD中;AD∥BC;∠D=75°;BC=6;CD=5;AD=10如图51点E在AD上;设t=BE+CE;求t2的最小值；2点F在AB上;将△BCF沿CF翻折;点B落在AD上的点G处;点G是AD的中点吗说明理由．。

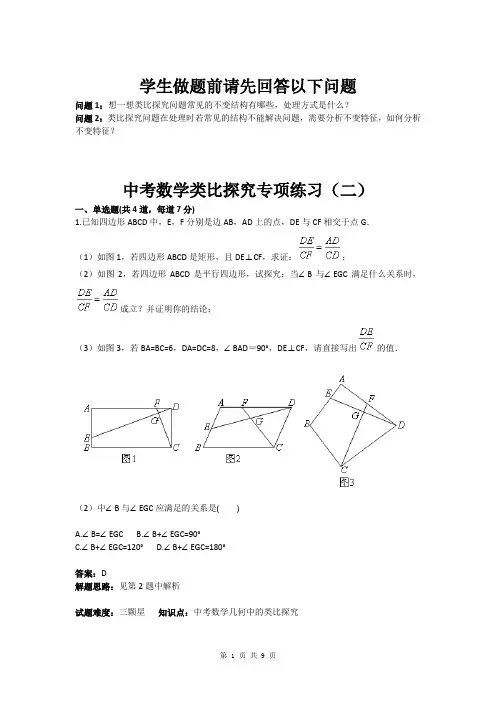
学生做题前请先回答以下问题问题1：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？问题2：类比探究问题在处理时若常见的结构不能解决问题，需要分析不变特征，如何分析不变特征？中考数学类比探究专项练习（二）一、单选题(共4道，每道7分)1.已知四边形ABCD中，E，F分别是边AB，AD上的点，DE与CF相交于点G．（1）如图1，若四边形ABCD是矩形，且DE⊥CF，求证：；（2）如图2，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；（3）如图3，若BA=BC=6，DA=DC=8，∠BAD＝90°，DE⊥CF，请直接写出的值．（2）中∠B与∠EGC应满足的关系是( )A.∠B=∠EGCB.∠B+∠EGC=90°C.∠B+∠EGC=120°D.∠B+∠EGC=180°答案：D解题思路：见第2题中解析试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（3）中的值为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究3.问题情境：张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，P为BC 边上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．小军的证明思路是：如图2，连接AP，由△ABP与△ACP的面积之和等于△ABC的面积可以证得：PD+PE=CF．小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．（1）变式探究：如图3，当点P在BC的延长线上时，其他条件不变，求证：PD-PE=CF；（2）结论运用：如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H，若AD=8，CF=3，求PG+PH的值；（3）迁移拓展：图5是一个航模的截面示意图，已知在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且，．M，N分别为AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．（2）中PG+PH的值为( )A.3B.4C.5D.答案：B解题思路：见第4题中解析试题难度：三颗星知识点：翻折变换（折叠问题）4.（上接第3题）（3）中△DEM与△CEN的周长之和为( )A.6B.C. D.答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边的一半。

类比探究专项训练（三）一、单选题(共5道，每道20分)1.在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD 之间的关系，小明准备分情况进行讨论．当E是AB中点时，如图1，小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，再由CE=DE可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．但是当E不是AB中点时，就不能照搬上述方式进行证明，此时小明想到了另外一种方式：过点E作EF∥BC，交AC于点F，也能证明AE=BD．（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要使用一对三角形全等，则证明此对三角形全等不能使用的条件是( )A.AASB.ASAC.SASD.SSS答案：D解题思路：1．解题要点①要在图2中照搬小明的思路，需要明白小明的思路在图1中是怎么证明的．考虑不能利用E是中点带来的结论，所以证明时，要避开中点带来的结论（AE=BE，∠ECB=30°），用其他条件来讨论．过点E作EF∥BC，交AC于点F，则△AEF是等边三角形，AE=EF=AF，能够证明△EFC≌△DBE，EF=BD，进而得到AE=BD．②在图2中，同样作出辅助线，如图所示，照搬①中的证明思路，先得到△AEF是等边三角形，AE=EF，再证明△EFC≌△DBE．关键在于判断三角形全等能够使用的条件有哪些．由题意得，BE=FC．∵∠ABC=∠AFE=60°，∴∠DBE=∠EFC=120°．∵∠D+∠DEB=60°，∠ECD+∠ECF=60°，∠D=∠ECD，∴∠DEB=∠ECF．同时∠D=∠ECD=∠CEF，即两个三角形中，三组内角分别对应相等，同时BE=CF，CE=DE，则证明△EFC≌△DBE可以使用AAS，ASA，SAS，不能使用的是SSS．③思考前面的证明过程，不变的特征是：△ABC是等边三角形，CE=DE．作平行线是为了得到等边三角形，进而得到全等三角形．④整个证明的路线图是：作辅助线；判断等边三角形（△AEF）；证明△EFC≌△DBE．2．解题过程我们利用SAS来证明AE=BD，具体过程如下：如图，过点E作EF∥BC，交AC于点F．则∠AEF=∠ABC=∠A=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠D=∠ECD．∵∠ABC=∠ACB，∴∠D+∠DEB=∠ECD+∠ECF，∴∠DEB=∠ECF，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）当点E在BA的延长线上时，如图3，点D在BC边上，且CE=DE，按照下面的操作，能够证明AE=BD的是( )A.直接证明△EAC≌△BDEB.①过点A作AF∥BC，交EC于点F；②△AEF是等边三角形；③△AFC≌△BDEC.①过点E作EF∥BC，交CA的延长线于点F；②△AEF是等边三角形；③△EFC≌△DBED.①过点A作AF∥BC，交EC于点F，连接DF；②四边形FDBE是等腰梯形答案：C解题思路：1．解题要点此题中△ABC是等边三角形及CE=DE没有发生变化，所以可照搬（1）中的思路．作辅助线；判断等边三角形（△AEF）；证明△EFC≌△DBE．作出的辅助线是：过点E作EF∥BC，交CA的延长线于点F．2．解题过程完整的证明过程如下：如图，过点E作EF∥BC，交CA的延长线于点F．则∠AEF=∠B=∠EAF=∠BAC=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠EDC=∠ECD，∴∠B+∠BED=∠ACB+∠FCE．∵∠B=∠ACB，∴∠BED=∠FCE，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．试题难度：三颗星知识点：中考数学几何中的类比探究3.正方形ABCD中，O是对角线AC的中点，P是对角线AC上一动点，连接PB．（1）过点P作PF⊥CD于点F，PE⊥PB，交CD（或CD的延长线）于点E，如图1和图2所示，则DF和EF之间的数量关系是( )A. B.C.DF=EFD.答案：C解题思路：①题目当中的一个明显特征是，∠BPE是斜直角，通过补成弦图的方式来处理问题：如图，延长FP，交AB于点G．则四边形AGFD是矩形，△AGP是等腰直角三角形．此时能够证明△PFE≌△BGP，∴EF=PG=AG=DF．②由于在图1和图2中，PB⊥PE没有发生变化，PF⊥CD也没有发生变化，所以可以通过相同的思路分析（相同的辅助线，相同的证明思路）．2．解题过程以图1为例，如图，延长FP，交AB于点G．易知四边形AGFD是矩形，△AGP是等腰直角三角形，∴AG=DF=PG，AD=GF=AB，∴BG=PF．又∵∠EFP=∠PGB，∠EPF=90°-∠GPB=∠PBG，∴△PFE≌△BGP，∴EF=PG，∴DF=EF．试题难度：三颗星知识点：中考数学几何中的类比探究4.（上接第3题）（2）在（1）中，当点P在线段OA上时，如图所示，则线段PA，PC，CE 之间的数量关系为( )A. B.C. D.答案：D解题思路：①由于PA，PC都是斜放置的线段，所以考虑借助图形中出现的等腰直角三角形，将PA，PC转到正方形的边上，利用正方形和等腰直角三角形边长之间的关系对目标进行研究．②借助于（1）中作出的辅助线，能够得到．这样就把PA，PC，CE之间的关系转化为三条线段CF，EF，CE之间的关系．③整个思考过程：DF=EF；利用等腰直角三角形的线段关系：；CF=CE+EF．2．解题过程如图，由（1）可知DF=EF．在等腰直角三角形AGP中，，在等腰直角三角形PFC中，，而CF=CE+EF，∴，∴，即线段PA，PC，CE之间的数量关系为．试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第3，4题）（3）在（1）中，当点P在线段OC上时（不与点O，C重合），类比（2）中的做法，可以判断线段PA，PC，CE之间的数量关系为( )A. B.C. D.答案：C解题思路：1．解题要点（2）和（3）的区别仅在于点P在线段OA上和点P在线段OC上．PF⊥CD，PE⊥PB没有发生变化，所以可照搬（2）中的思路．2．解题过程如图，延长FP，交AB于点G，由（1）可知DF=EF．在等腰直角三角形AGP中，，在等腰直角三角形PFC中，，而CF=EF-CE，∴，∴，即线段PA，PC，CE之间的数量关系为．试题难度：三颗星知识点：中考数学几何中的类比探究。

类比探究综合测试（四）一、单选题(共6道，每道16分)1.在正方形ABCD中，对角线AC，BD相交于点O，点P在线段BC上（不与点B重合），且，PE交OB于点E，过点B作BF⊥PE于点F，交AC于点G．（1）如图1，当点P与点C重合时，的值为( )A.1B.C. D.答案：B解题思路：如图1，∵四边形ABCD是正方形，∴OB=OP，∠EOP=∠GOB=90°，∴∠1+∠2=90°．∵PF⊥BG，，∴，∠1+∠3=90°，∴∠2=∠3，∴△GOB≌△EOP（AAS），∴BG=PE，∴．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）如图2，当点P与点C不重合时，通过观察、测量、猜想，可得的值为( )A.1B.C. D.答案：B解题思路：如图2，过点P作PM//AC，交BG于点M，交BD于点N．∵四边形ABCD是正方形，∴∠BOC=90°，∠OBC=45°．∵PM//AC，∴∠BPM=∠ACB，∠MNB=∠ENP=90°，∴△BNP是等腰直角三角形，BN=PN，∠1+∠2=90°．∵PF⊥BG，，∴∠1+∠3=90°，，∴∠2=∠3，，∴△BMN≌△PEN（AAS），∴BM=PE，∴．试题难度：三颗星知识点：中考数学几何中的类比探究3.（上接第1，2题）（3）如图3，把题干中的正方形ABCD改为菱形，其他条件不变，若∠ACB=α，则的值为( )（用含α的式子表示）A. B.tanαC. D.答案：D解题思路：如图3，过点P作PM//AC，交BG于点M，交BD于点N．∵四边形ABCD是菱形，∴∠BOC=90°．∵PM//AC，∴∠BPM=∠ACB=α，∠MNB=∠ENP=90°，∴∠1+∠2=90°．∵PF⊥BG，，∴∠1+∠3=90°，，∴∠2=∠3，，∴△BMN∽△PEN，∴．∵，∴．在Rt△BNP中，，∴．试题难度：三颗星知识点：中考数学几何中的类比探究4.将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得到，我们将这种变换记为[θ，n]．（1）如图1，对△ABC作变换[60，]，得到，则的值为_______，直线BC与直线所夹的锐角为______．( )A. B.C. D.答案：D解题思路：如图1，由题意，，∴，．又∵∠1=∠2，∴，即直线BC与直线所夹的锐角为60°．试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第4题）（2）如图2，在△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]，得，使点在同一条直线上，且四边形为矩形，则θ和n的值分别为( )A. B.C. D.答案：D解题思路：∵四边形为矩形，∴．∵∠BAC=30°，∴，即θ=60．在中，∵，∴，即n=2．综上，θ和n的值分别为60，2．试题难度：三颗星知识点：中考数学几何中的类比探究6.（上接第4，5题）（3）如图3，在△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]，得，使点在同一条直线上，且四边形为平行四边形，则θ和n的值分别为( )A. B.C. D.答案：C解题思路：∵AB=AC，∠BAC=36°，∴∠ABC=∠ACB=72°．由题意，．∵四边形为平行四边形，∴AC′∥BB′，∴，∴，∴，∴．∵，∴，∴．设AB=x，则，∴，∴，∴，∴．综上，θ和n的值分别为．试题难度：三颗星知识点：中考数学几何中的类比探究。

中招考试几何类比探究题集锦（附参考答案）参考答案与试题解析一．解答题（共11小题）1．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ABD≌△ACF；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，请直接写出DE2，BD2，CE2三者之间的等量关系．【解答】解：（1）∵点D关于直线AE的对称点为F，∴EF=DE，AF=AD，∠DAE=∠EAF=α∴∠CAE+∠CAF=α∵∠BAC=2∠DAE=2α．∴∠BAD+∠CAE=∠BAC﹣∠DAE=α，∴∠BAD=∠CAF，在△ABD和△ACF中，第1页（共33页）第2页（共33页）∴△ABD ≌△ACF （SAS ），（2）由（1）知，△ABD ≌△ACF （SAS ），∴CF=BD ，∠ACF=∠B ，∵AB=AC ，∠BAC=2α，α=45°，∴△ABC 是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB +∠ACF=45°+45°=90°，在Rt △CEF 中，由勾股定理得，EF 2=CF 2+CE 2，∴DE 2=BD 2+CE 2，（3）DE 2=BD 2+CE 2；理由：如图，∵∠BAC=2∠DAE=2α．∴∠DAE=α，∵点D 关于直线AE 的对称点为F ，∴EF=DE ，AF=AD ，∠DAE=∠EAF=α∴∠CAF=∠EAF +∠CAE=α+∠CAE∴∠BAD=∠BAC ﹣∠DAC=2α﹣∠DAC=2α﹣（∠DAE ﹣∠CAE ）=2α﹣（α﹣∠CAE）=α+∠CAE∴∠BAD=∠CAF，在△ABD和△ACF中，∴△ABD≌△ACF（SAS），∴CF=BD，∠ACF=∠B，∵AB=AC，∠BAC=2α，α=45°，∴△ABC是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB+∠ACF=45°+45°=90°，在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，∴DE2=BD2+CE2，2．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系（直接写出结果即可）．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第（1）题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF 均为等第3页（共33页）边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．【解答】解：（1）DE=BD+CE．理由如下：如图1，∵BD⊥l，CE⊥l，∴∠BDA=∠AEC=90°又∵∠BAC=90°，∴∠BAD+∠CAE=90°，∠BAD+∠ABD=90°，∴∠CAE=∠ABD在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD；（2）如图2，∵∠BDA=∠AEC=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α，第4页（共33页）∴∠CAE=∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE；（3）DF=EF．理由如下：由（2）知，△ADB≌△CAE，BD=EA，∠DBA=∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°，∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE，∵BF=AF在△DBF和△EAF中，，∴△DBF≌△EAF（SAS），∴DF=EF，∠BFD=∠AFE，第5页（共33页）∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形．∴DF=EF．3．（1）问题发现如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：①∠ACE的度数为60°；②线段AC、CD、CE之间的数量关系为AC=CD+CE．（2）拓展探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC 上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．（3）解决问题如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．第6页（共33页）【解答】解：（1）①∵△ABC和△ADE均为等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=∠B=60°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE=∠B=60°，故答案为：60°；②线段AC、CD、CE之间的数量关系为：AC=CD+CE；理由是：由①得：△BAD≌△CAE，∴BD=CE，∵AC=BC=BD+CD，∴AC=CD+CE；故答案为：AC=CD+CE；（2）∠ACE=45°，AC=CD+CE，理由是：如图2，∵△ABC和△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，∴AB=AC，AD=AE，∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，第7页（共33页）∴△ABD≌△ACE，∴BD=CE，∠ACE=∠B=45°，∵BC=CD+BD，∴BC=CD+CE，∵在等腰直角三角形ABC中，BC=AC，∴AC=CD+CE；（3）如图3，过A作AC的垂线，交CB的延长线于点F，∵∠BAD=∠BCD=90°，AB=AD=2，CD=1，∴BD=2，BC=，∵∠BAD=∠BCD=90°，∴∠BAD+∠BCD=180°，∴A、B、C、D四点共圆，∴∠ADB=∠ACB=45°，∴△ACF是等腰直角三角形，由（2）得：AC=BC+CD，∴AC===．第8页（共33页）4．【探究发现】如图1，△ABC是等边三角形，∠AEF=60°，EF交等边三角形外角平分线CF所在的直线于点F，当点E是BC的中点时，有AE=EF成立；【数学思考】某数学兴趣小组在探究AE、EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（B，C除外）任意一点时（其它条件不变），结论AE=EF仍然成立．假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在备用图1中画出图形，并证明AE=EF．【拓展应用】当点E在线段BC的延长线上时，若CE=BC，在备用图2中画出图形，并运用上述结论求出S△ABC ：S△AEF的值．【解答】证明：第一种情况：点E是线段BC上的任意一点，可作三种辅助线：方法一：如图1，在AB上截取AG，使AG=EC，连接EG，第9页（共33页）∵△ABC是等边三角形，∴AB=BC，∠B=∠ACB=60°．∵AG=EC，∴BG=BE，∴△BEG是等边三角形，∠BGE=60°，∴∠AGE=120°．∵FC是外角的平分线，∠ECF=120°=∠AGE．∵∠AEC是△ABE的外角，∴∠AEC=∠B+∠GAE=60°+∠GAE．∵∠AEC=∠AEF+∠FEC=60°+∠FEC，∴∠GAE=∠FEC．在△AGE和△ECF中，∴△AGE≌△ECF（ASA），∴AE=EF；方法二：在CA上截取CG=CE，连结GE，证明类似方法一；方法三：延长FC到G，使CG=CE，连结EG，易证△CEG是等边三角形，第10页（共33页）∴CE=EG，∠G=∠ACB=60°，∠CEG=∠AEF=60°，∴∠CEG+∠CEF=∠AEF+∠CEF，即∠GEF=∠AEC，∴△GEF≌△CEA，∴AE=EF．第二种情况：点E是线段BC延长线上的任意一点如图2，可作三种辅助线：①在CF上截取CG=CE，连接GE②延长AC到G，使CG=CE，连结EG；③或延长BA到G，使BG=BE，连结EG．第②种添加辅助线的方法证明如下：证明：延长AC到G，使CG=CE，连结EG，易证△CEG为等边三角形，∴∠G=∠ECF=60°，EG=CE，又∠AEG=∠CEG+∠AEC=60°+∠AEC，∠CEF=∠AEF+∠AEC=60°+∠AEC，第11页（共33页）∴∠AEG=∠CEF，∴△AEG≌△FEC，∴AE=EF．第三种情况：点E是线段BC反向延长线上的任意一点如图3，可作三种辅助线：①延长AB到G，使BG=BE，连结EG；②延长CF到G，使CG=CE，连结EG；③在CE上截取CG=CF，连结GF现就第①种添加辅助线的方法证明如下：证明：延长AB到G，使BG=BE，连结EG，易证△BEG为等边三角形，∴∠G=∠ECF=60°，第12页（共33页）∵∠AEB+∠BAE=∠ABC=60°，∠AEB+∠CEF=∠AEF=60°，∴∠BAE=∠CEF，∵AB=BC，BG=BE，∴AB+BG=BC+BE，即AG=CE，∴△AEG≌△EFC，∴AE=EF．拓展应用：如图4：作CH⊥AE于H点，∴∠AHC=90°．由数学思考得AE=EF，又∵∠AEF=60°，∴△AEF是等边三角形，∴△ABC∽△AEF．第13页（共33页）∵CE=BC=AC，△ABC是等边三角形，∴∠CAH=30°，AH=EH．∴CH=AC，AH=AC，AE=AC，∴．∴==．5．问题情境：在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．（1）操作发现：当点O为AC中点时：①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系：AE2+CF2=EF2（无需证明）；②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的结论是否成立．若成立，请证明；若不成立，请说明理由；第14页（共33页）（2）类比延伸：当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若=，请直接写出=．【解答】解：（1）①猜想：AE2+CF2=EF2，连接OB，如图1，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB+∠BOF=∠FOC+∠BOF．∴∠EOB=∠FOC，在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；故答案为：AE2+CF2=EF2；第15页（共33页）②成立．证明：连结OB．如图2，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB=∠FOC．在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；（2）=，如图3，过点O作OM⊥AB于M，ON⊥BC于N．∵∠B=90°，第16页（共33页）∴∠MON=90°，∵∠EOF=90°，∴∠EOM=∠FON．∵∠EMO=∠FNO=90°，∴△OME∽△ONF，∴=，∵△AOM和△OCN为等腰直角三角形，∴△AOM∽△OCN，∴=，∵=，∴=，故答案为．第17页（共33页）第18页（共33页）6．阅读发现：（1）如图①，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，AB=BC=3，BD=BE=1，连结CD ，AE ．易证：△BCD ≌△BAE ．（不需要证明） 提出问题：（2）在（1）的条件下，当BD ∥AE 时，延长CD 交AE 于点F ，如图②，求AF 的长．解决问题：（3）如图③，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，连结CD ，AE ．当∠BAE=45°时，点E 到AB 的距离EF 的长为2，求线段CD的长为 ．【解答】（2）解：如图②中，AB与CF交于点O．由（1）可知：△BCD≌△BAE，∴∠OAF=∠OCB，CD=AE，∵∠AOF=∠COB，∴∠AFO=∠CBO=90°，∴CF⊥AE，∵BD∥AE，∴BD⊥CF，在RT△CDB中，∵∠CDB=90°，BC=3，BD=1，∴CD=AE==2，∵∠BDF=∠DFE=∠DBE=90°，∴四边形EFDB是矩形，∴EF=BD=1，∴AF=AE﹣EF=2﹣1．（3）解：在RT△ABC，RT△EBD中，∵∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，∴AB=BC，BE=BD，∴==，∵∠ABC=∠EBD=90°，∴∠ABE=∠DBC，∴△ABE∽△CBD，∴==，第19页（共33页）第20页（共33页）在RT △AEF 中，∵∠AFE=90°，∠EAF=45°，EF=2，∴AF=EF=2，AE=2，∴=，∴CD=．故答案为．7．如图1，两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现：如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，请猜想（1）中S1与S2的数量关系是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）拓展探究已知∠ABC=60°，BD平分∠ABC，BD=CD，BC=9，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请求相应的BF的长．【解答】解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC=CD，∵∠BAC=90°﹣∠B=90°﹣30°=60°，第21页（共33页）∴△ACD是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE，∴DE∥AC；故答案为：DE∥AC；②∵∠B=30°，∠C=90°，∴CD=AC=AB，∴BD=AD=AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2=×2×2=2；故答案为：S1=S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°﹣90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，，第22页（共33页）∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF1=S△BDE；过点D作DF2⊥BD，∵∠ABC=60°，F1D∥BE，∴∠F2F1D=∠ABC=60°，∵BF1=DF1，∠F1BD=∠ABC=30°，∠F2DB=90°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=×60°=30°，∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°，∠CDF2=360°﹣150°﹣60°=150°，∴∠CDF1=∠CDF2，第23页（共33页）∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=×60°=30°，又∵BD=4，∴BE=×6÷cos30°=3÷=2，∴BF1=2，BF2=BF1+F1F2=2+2=4，故BF的长为2或4．8．问题解决：如图（1），将正方形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN．当时，求的值．类比归纳：第24页（共33页）在图（1）中，若，则的值等于；若，则的值等于；若（n 为整数），则的值等于．（用含n的式子表示）联系拓广：如图（2），将矩形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN，设，则的值等于．（用含m，n的式子表示）【解答】解：（1）方法一：如图（1﹣1），连接BM，EM，BE．由题设，得四边形ABNM和四边形FENM关于直线MN对称．∴MN垂直平分BE，∴BM=EM，BN=EN．∵四边形ABCD是正方形，∴∠A=∠D=∠C=90°，设AB=BC=CD=DA=2．∵，∴CE=DE=1．第25页（共33页）设BN=x，则NE=x，NC=2﹣x．在Rt△CNE中，NE2=CN2+CE2．∴x2=（2﹣x）2+12，解得x=，即BN=．在Rt△ABM和在Rt△DEM中，AM2+AB2=BM2，DM2+DE2=EM2，∴AM2+AB2=DM2+DE2．设AM=y，则DM=2﹣y，∴y2+22=（2﹣y）2+12，解得y=，即AM=（6分）∴．方法二：同方法一，BN=．如图（1﹣2），过点N做NG∥CD，交AD于点G，连接BE．∵AD∥BC，∴四边形GDCN是平行四边形．∴NG=CD=BC．同理，四边形ABNG也是平行四边形．∴AG=BN=∵MN⊥BE，∴∠EBC+∠BNM=90度．∵NG⊥BC，∴∠MNG+∠BNM=90°，第26页（共33页）∴∠EBC=∠MNG．在△BCE与△NGM中，∴△BCE≌△NGM，EC=MG．∵AM=AG﹣MG，AM=﹣1=．∴．（2）如图1，当四边形ABCD为正方形时，连接BE，=，不妨令CD=CB=n，则CE=1，设BN=x，则EN=x，EN2=NC2+CE2，x2=（n﹣x）2+12，x=；作MH⊥BC于H，则MH=BC，又点B，E关于MN对称，则MN⊥BE，∠EBC+∠BNM=90°；而∠NMH+∠BNM=90°，故∠EBC=∠NMH，则△EBC≌△NMH，∴NH=EC=1，AM=BH=BN﹣NH=﹣1=则：==．故当=，则的值等于；若=，则的值等于；第27页（共33页）（3）若四边形ABCD为矩形，连接BE，=，不妨令CD=n，则CE=1；又==，则BC=mn，同样的方法可求得：BN=，BE⊥MN，易证得：△MHN∽△BCE．故=，=，HN=，故AM=BH=BN﹣HN=，故==．故答案为：；；；．第28页（共33页）第29页（共33页）9．阅读理解：如图1，在直角梯形ABCD 中，AB ∥CD ，∠B=90°，点P 在BC 边上，当∠APD=90°时，易证△ABP ∽△PCD ，从而得到BP•PC=AB•CD ，解答下列问题．（1）模型探究：如图2，在四边形ABCD 中，点P 在BC 边上，当∠B=∠C=∠APD 时，结论BP•PC=AB•CD 仍成立吗？试说明理由；（2）拓展应用：如图3，M 为AB 的中点，AE 与BD 交于点C ，∠DME=∠A=∠B=45°且DM 交AC 于F ，ME 交BC 于G ．AB=，AF=3，求FG 的长．【解答】解：（1）∵∠APC=∠APD +∠CPD ，∠APC=∠BAP +∠B （三角形外角定理），∠B=∠APD （已知），∴∠BAP=∠CPD，又∵∠B=∠C，∴△ABP∽△PCD∴=，∴BP•PC=AB•CD；（2）∵∠AFM=∠DME+∠E（三角形外角定理），∠DME=∠A（已知），∴∠AFM=∠A+∠E（等量代换），又∠BMG=∠A+∠E（三角形外角定理），∴∠AFM=∠BMG．∵∠A=∠B，∴△AMF∽△BGM．当∠A=∠B=45°时，∠ACB=180°﹣∠A﹣∠B=90°，即AC⊥BC且AC=BC．∵M为AB的中点，∴AM=BM=，AC=BC=4．又∵△AMF∽△BGM，∴，∴BG===，又∵，CF=4﹣3=1，∴．第30页（共33页）10．基本模型如下图，点B、P、C在同一直线上，若∠B=∠1=∠C=90°，则△ABP∽△PCD成立，（1）模型拓展如图1，点B、P、C在同一直线上，若∠B=∠1=∠C，则△ABP∽△PCD成立吗？为什么？（2）模型应用①如图2，在等腰梯形ABCD中，AD∥BC，AD=1，AB=2，BC=4，在BC上截取BP=AD，作∠APQ=∠B，PQ交CD于点Q，求CQ的长；②如图3，正方形ABCD的边长为1，点P是线段BC上的动点，作∠APQ=90°，PQ交CD于Q，当P在何处时，线段CQ最长？最长是多少？【解答】解：（1）成立，∵∠A=180°﹣（∠B+∠APB），第31页（共33页）∠CPD=180°﹣（∠1+∠APB），∠B=∠1，∴∠A=∠CPD，∵∠B=∠C，∴△ABP∽△PCD；（2）①∵四边形ABCD是等腰梯形，∴∠B=∠C，∵∠B=∠APQ，∴∠B=∠APQ=∠C，由（1）知，△ABP∽△PCD，∴=，∴=，∴CQ=；②设BP=x，CQ=y．∵∠B=∠APQ=90°，∴△ABP∽△PCQ，∴=，即=，∴y=﹣x2+x=﹣（x﹣）2+，第32页（共33页）∴当x=时，y=，最大即当P是BC的中点时，CQ最长，最长为．第33页（共33页）。

类比探究专题1. 如图1，在Rt △ABC 中，∠BAC =90°，AB =AC ，点D ，E 分别在边AB ，AC上，AD =AE ，连接DC ，BE ，点P 为DC 的中点． （1）观察猜想图1中，线段AP 与BE 的数量关系是________，位置关系是________； （2）探究证明把△ADE 绕点A 逆时针方向旋转到图2的位置，小航猜想（1）中的结论仍然成立，请你证明小航的猜想； （3）拓展延伸把△ADE 绕点A 在平面内自由旋转，若AD =4，AB =10，请直接写出线段AP 的取值范围．（1）操作：如图1，点O 为线段MN 的中点，直线PQ 与MN 相交于点O ，请利用图1画出一对以点O 为对称中心的全等三角形．（不写画法）根据上述操作得到的经验完成下列探究活动：（2）探究一：如图2，在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE =∠EAF ，AF 与DC 的延长线相交于点F ．试探究线段AB 与AF ，CF 之间的等量关系，并证明你的结论． （3）探究二：如图3，DE ，BC 相交于点E ，BA 交DE 于点A ，且BE :EC =1:2，∠BAE =∠EDF ，CF ∥AB ．若AB =5，CF =1，求DF 的长度．PEDA BC 图1PEDABC图2图1M NQ PO图2F EDC B AAB C D E F图32.特殊：（1）如图1，在等腰直角三角形ABC中，∠ACB=90°．作CM平分∠ACB交AB于点M，点D为射线CM上一点，以点C为旋转中心将线段CD逆时针旋转90°得到线段CE，连接DE交射线CB于点F，连接BD，BE．填空：①线段BD，BE的数量关系为_________________；②线段BC，DE的位置关系为_________________．一般：（2）如图2，在等腰三角形ABC中，∠ACB=α，作CM平分∠ACB交AB于点M，点D为△ABC外部射线CM上一点，以点C为旋转中心将线段CD逆时针旋转α度得到线段CE，连接DE，BD，BE．请判断（1）中的结论是否成立，请说明理由．特殊：（3）如图3，在等边三角形ABC中，作BM平分∠ABC交AC于点M，点D为射线BM上一点，以点B为旋转中心将线段BD逆时针旋转60°得到线段BE，连接DE交射线BA于点F，连接AD，AE．若AB=4，当△ADM 与△AFD全等时，请直接写出DE的值．M F ED CB A图1EMDCBA图2MFEDC BA图33. 已知△ABC 中，CA =CB ，0°＜∠ACB ≤90°．点M ，N 分别在边CA ，CB 上（不与端点重合），BN =AM ，射线AG ∥BC 交BM 延长线于点D ，点E 在直线AN 上，EA =ED ．（1）【观察猜想】如图1，点E 在射线NA 上，当∠ACB =45°时， ①线段BM 与AN 的数量关系是_________； ②∠BDE 的度数是____________．（2）【探究证明】如图2，点E 在射线AN 上，当∠ACB =30°时，判断并证明线段BM 与AN 的数量关系，求∠BDE 的度数；（3）【拓展延伸】如图3，点E 在直线AN 上，当∠ACB =60°时，AB =3，点N 是BC 边上的三等分点，直线ED 与直线BC 交于点F ，请直接写出线段CF 的长．图1A B CD ENMG图2AB CD MN EG 图3A BCG4.如图，在Rt△ABC中，∠ACB=90°，BC mAC n=，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m=n，点E在线段AC上，则DEDF=__________．（2）数学思考：①如图2，若点E在线段AC上，则DEDF=__________（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明．（3）拓展应用：若ACBC=DF=CE的长．FEDC BA图1图2ABCDEFDB FECA图3DC BA备用图5. （1）【问题发现】如图1，△ABC 和△CEF 都是等腰直角三角形，∠BAC =∠EFC =90°，点E 与点A 重合，则线段BE 与AF 的数量关系为__________； （2）【拓展研究】在（1）的条件下，将△CEF 绕点C 旋转，连接BE ，AF ，线段BE 与AF 的数量关系有无变化？仅就图2的情形给出证明； （3）【问题发现】当AB =AC =2，△CEF 旋转到B ，E ，F 三点共线时，直接写出线段AF 的长．（1）问题发现：如图1，在△ABC 中，∠BAC =90°，AB =AC ，点D 是BC 的中点，以点D 为顶点作正方形DFGE ，使点A ，C 分别在DE 和DF 上，连接BE ，AF ，则线段BE 和AF 数量关系是________．（2）类比探究：如图2，保持△ABC 固定不动，将正方形DFGE 绕点D 旋转α（0＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC =DF =2，在（2）的旋转过程中，连接AE ，请直接写出AE 的最大值．F图1CBA (E )EABC图2F备用图CBA图1A BC DEF G图2GFED CB A 备用图A BC DEFG6.在菱形ABCD中，∠ABC=60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．（1）如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是__________，CE与AD的位置关系是__________．（2）当点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（选择图2，图3中的一种情况予以证明）．（3）如图4，当点P在线段BD的延长线上时，连接BE，若AB=BE= ADPE的面积．（直接写出结果）P EDCBA图1图2ABCDEPPEDCBA图3图4ABCDEP7. （1）操作发现如图1，AD 是等边三角形ABC 的角平分线，请你按下列要求画图：过点A 作AM ⊥AB ，过点C 作CN ∥AB ，AM 与CN 相交于点E ．则AD 与AE 的数量关系是________，∠EAC =________°． （2）问题探究将图1中的△AEC 绕点A 逆时针旋转，点C 落在点F 的位置，连接EC ，DF ，如图2所示，请你探究DF 与EC 的数量关系并说明理由． （3）拓展延伸若（2）中等边△ABC 的边长为2，当F A ⊥AC 时，请直接写出DF 2的值．在Rt △ABC 中，∠BAC =90°，AC =AB =4，D ，E 分别是边AB ，AC 的中点，若等腰Rt △ADE 绕点A 逆时针旋转，得到等腰Rt △AD 1E 1，设旋转角为α（0＜α≤180°），记直线BD 1与CE 1的交点为P ．（1）问题发现如图1，当α=90°时，线段BD 1的长等于__________，线段CE 1的长等于__________． （2）探究证明如图2，当α=135°时，求证：BD 1=CE 1，且BD 1⊥CE 1． （3）问题解决求点P 到AB 所在直线的距离的最大值．（直接写出结果）图1AB CD图2EFDCBA备用图CBAE1(D1)ABCDE PEDCBAD1E1图2图18. 如图1，在正方形ABCD 和正方形AB′C′D′中，AB =2，AB′=，连接CC′．（1）问题发现：CC BB'='__________；（2）拓展探究：将正方形AB′C′D′绕点A 逆时针旋转，记旋转角为θ，连接BB′，试判断：当0°≤θ＜360°时，CC BB ''的值有无变化？请仅就图2中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C ，C′，D′三点共线时BB′的长．问题发现：如图1，△ABC 是等边三角形，点D 是边AB 上的一点，过点D 作DE ∥BC 交AC 于E ，则线段BD 与CE 的数量关系为___________；拓展探究：如图2，将△ADE 绕点A 逆时针旋转角α（0°＜α＜360°），上面的结论是否仍然成立？如果成立，请就图中给出的情况加以证明；问题解决：如果△ABC的边长等于AD =2，直接写出当△ADE 旋转到DE 与AC 所在的直线垂直时BD 的长．D′C′B′ABCD 图1图2DCBA B′C′D′A BCD备用图图1EDCBA 图2ABCDE备用图E D A9. 如图1，已知点G 在正方形ABCD 的对角线AC 上，GE ⊥BC ，垂足为点E ，GF ⊥CD ，垂足为点F ． （1）证明与推断：①求证：四边形CEGF 是正方形；②推断AGBE的值为_______．（2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转α角（0°＜α＜45°），如图2所示，试探究线段AG 与BE 之间的数量关系，并说明理由． （3）拓展与运用：正方形CEGF 在旋转过程中，当B ，E ，F 三点在一条直线上时，如图3所示，延长CG 交AD 于点H ．若AG =6，GH=BC =________．GFDC BAE图1ABCD EFG图2H GF EDCBA 图310. （1）阅读理解利用旋转变换解决数学问题是一种常用的方法．如图1，点P 是等边三角形ABC 内一点，P A =1，PB，PC =2．求∠BPC 的度数． 为利用已知条件，不妨把△BPC 绕点C 顺时针旋转60°得△AP′C ，连接PP′，则PP′的长为__________；在△P AP′中，易证∠P AP′=90°，且∠PP′A 的度数为__________，综上可得∠BPC 的度数为__________． （2）类比迁移 如图2，点P 是等腰Rt △ABC 内一点，∠ACB =90°，P A =2，PB，PC =1．求∠APC 的度数． （3）拓展应用如图3，在四边形ABCD 中，BC =3，CD =5，AB =AC =12AD ，∠BAC =2∠ADC ，请直接写出BD 的长．P′ABCP图1图2P CBAD图3C BA11. 如图，在□ABCD 中，AC 与BD 交于点O ，以点O 为顶点的∠EOF 的两边分别与边AB ，AD 交于点E ，F ，且∠EOF 与∠BAD 互补． （1）观察猜想若四边形ABCD 是正方形，则线段OE 与OF 有何数量关系？请直接写出结论．（2）延伸探究若四边形ABCD 是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由． （3）拓展证明若AB :AD =m :n ，探索线段OE 与OF 的数量关系，并证明你的结论．（1）阅读理解：如图1，在四边形ABCD 中，AB ∥DC ，E 是BC 的中点，若AE 是∠BAD 的平分线，试判断AB ，AD ，DC 之间的等量关系．解决此问题可以用如下方法：延长AE 交DC 的延长线于点F ，易证△AEB ≌△FEC ，得到AB =FC ，从而把AB ，AD ，DC 转化在一个三角形中即可判断．AB ，AD ，DC 之间的等量关系为_____________；（2）问题探究：如图2，在四边形ABCD 中，AB ∥DC ，AF 与DC 的延长线交于点F ，E 是BC 的中点，若AE 是∠BAF 的平分线，试探究AB ，AF ，CF 之间的等量关系，并证明你的结论．（3）问题解决：如图3，AB ∥CF ，AE 与BC 交于点E ，BE :EC =2:3，点D 在线段AE 上，且∠EDF =∠BAE ，试判断AB ，DF ，CF 之间的数量关系，并证明你的结论．A BCDOEFABCD EF图1ABCDE F图2A BCDE F图312. 如图1，菱形ABCD 与菱形GECF 的顶点C 重合，点G 在对角线AC 上，且∠BCD =∠ECF =60°． （1）问题发现： AGBE的值为__________． （2）探究与证明：将菱形GECF 绕点C 按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG 与BE 之间的数量关系，并说明理由． （3）拓展与运用：菱形GECF 在旋转过程中，当点A ，G ，F 三点在一条直线上时，如图3所示，连接CG 并延长，交AD 于点H ，若CE =2，GHAH 的长为__________．已知∠AOB =90°，点C 是∠AOB 的角平分线OP 上的任意一点，现有一个直角∠MCN 绕点C 旋转，两直角边CM ，CN 分别与直线OA ，OB 相交于点D ，点E ．（1）如图1，若CD ⊥OA ，猜想线段OD ，OE ，OC 之间的数量关系，并说明理由．（2）如图2，若点D 在射线OA 上，且CD 与OA 不垂直，则（1）中的数量关系是否仍成立？如成立，请说明理由；如不成立，请写出线段OD ，OE ，OC 之间的数量关系，并加以证明．图1AB CDEFGG FE DCB A图2H图3AB CD E FG（3）如图3，若点D 在射线OA 的反向延长线上，且OD =2，OE =8，请直接写出线段CE 的长度．图1OABC D EMPN N PMED CBAO图2图3O ABCD E MPN13.如图，在矩形ABCD中，AB=8，AD=6，点E，F分别是边DC，DA的中点，四边形DFGE为矩形，连接BG．（1）问题发现在图1中，CEBG__________．（2）拓展探究将图1中的矩形DFGE绕点D旋转一周，在旋转过程中，CEBG的大小有无变化？请仅就图2的情形给出证明． （3）问题解决当矩形DFGE 旋转至B ，G ，E 三点共线时，请直接写出线段CE 的长．GFED CBA 图1图2ABCDEFG备用图ABCD14. 四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD 等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD 中，AB =AD ，CB =CD ，则AC 与BD 的位置关系是__________，请说明理由．（2）试探究图1中四边形ABCD 的两组对边AB ，CD 与BC ，AD 之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt △ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ，连接CE ，BG ，GE ，已知AC =4，AB =5，求GE 的长．观察猜想（1）如图1，在Rt △ABC 中，∠BAC =90°，AB =AC =3，点D 与点A 重合，点E 在边BC 上，连接DE ，将线段DE 绕点D 顺时针旋转90°得到线段DF ，连接BF ，BE 与BF 的位置关系是_________，BE +BF =_________； 探究证明（2）在（1）中，如果将点D 沿AB 方向移动，使AD =1，其余条件不变，如图2，判断BE 与BF 的位置关系，并求BE +BF 的值，请写出你的理由或计算过程； 拓展延伸ABCD图1图2DCB AABCDEFG图3（3）如图3，在△ABC 中，AB =AC ，∠BAC =α，点D 在边BA 的延长线上，BD =n ，连接DE ，将线段DE 绕着点D 顺时针旋转，旋转角∠EDF =α，连接BF ，则BE +BF 的值是多少？请用含有n ，α的式子直接写出结论．图1A (D )B CE FD FE C B A 图2图3A C D E F。

中考数学几何中的类比探究综合测试卷一、单选题(共6道，每道16分)1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(1)当∠MAN绕点A旋转到BM=DN时(如图1),线段BM、DN、MN之间的数量关系为()A.BM+DN=MNB.BM+DN=MNC.BM+DN=MND.不能确定答案：A试题难度：三颗星知识点：类比探究问题2.已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.小明猜测线段BM,DN和MN之间的数量关系为BM+DN=MN.理由如下:如图, ① .∵四边形ABCD是正方形, ∴AB=AD,∠D=∠ABC=∠ABE =90°, ∴△ABE≌△ADN, ∴∠BAE=∠DAN,AE=AN, ∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°, ∵∠MAN=45°, ∴∠EAM=45°, 又∵AM=AM, ∴② , ∴MN=ME,∵ME=BM+BE=BM+DN, ∴BM+DN=MN. ①,②处横线上所填内容分别是()A.延长BC至点E,使得BE=DN;△EAM≌△NAMB.延长CB至点E,使得BE=CN;△EAM≌△NAMC.延长CB至点E,使得BE=DN;△EAM≌△NAMD.延长CB至点E,使得BE=DN;△EMA≌△NAM答案：C试题难度：三颗星知识点：类比探究问题3.已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间的数量关系为()A.BM+DN=MNB.DN -BM =MNC.DN - MN =2 BMD.BM+DN=2MN答案：B试题难度：三颗星知识点：类比探究问题4.在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(1)若点E是线段AC的中点,如图1,则BE与EF的数量关系为BEEF;A.>B.=C.<D.不能确定答案：B试题难度：三颗星知识点：类比探究问题5.在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(2)若点E是线段AC上的任意一点,其它条件不变.如图2,判断线段BE、EF有怎样的数量关系并证明.小宇同学展示出如下正确的作法:解:BE=EF,证明如下:如图2, ① ,∵四边形ABCD为菱形, ∴AB=BC, 又∵∠ABC=60°, ∴△ABC是等边三角形, ∴AB=AC,∠ACB=60°, 又∵EG∥BC, ∴∠AGE=∠ABC=60°, 又∵∠BAC=60°, ∴△AGE是等边三角形, ∴AG=AE, ∴BG=CE, 又∵CF=AE, ∴GE=CF, 又∵∠BGE=∠ECF=120°, ∴② , ∴BE=EF; ①,②处横线上所填内容分别是()A.过点E作EG∥BC,交AB于点G;△BAE≌△ECFB.过点E作EG∥BC,交AB于点G;△BGE≌△EFCC.过点E作EG∥BC,交AB于点G;△BGE≌△ECFD.过点E作EG∥BC,交AB于点G;△BEA≌△ECF答案：C试题难度：三颗星知识点：类比探究问题6.在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(3)如图3,若点E是线段AC延长线上的任意一点,其它条件不变.求证:BE=EF.参考小宇同学的作法,第一步应为③ .接下来的证明过程如下:∵四边形ABCD为菱形, ∴AB=BC, 又∵∠ABC=60°, ∴△ABC是等边三角形, ∴AB=AC,∠ACB=60°, 又∵EG∥BC, ∴∠AGE=∠ABC=60°, 又∵∠BAC=60°, ∴△AGE是等边三角形, ∴AG=AE, ∴BG=CE, 又∵CF=AE, ∴GE=CF, 又∵∠BGE=∠ECF=60°, ∴④ , ∴BE=EF. ③,④处横线上所填内容分别是()A.过点E作EG∥BC,交BA延长线于点G;△BGE≌△ECFB.过点E作EG∥BC,交AB延长线于点G;△BCE≌△FECC.过点E作EG∥BC,交BA延长线于点G;△BCE≌△FECD.过点E作EG∥BC,交AB延长线于点G;△BGE≌△ECF答案：D试题难度：三颗星知识点：类比探究问题。

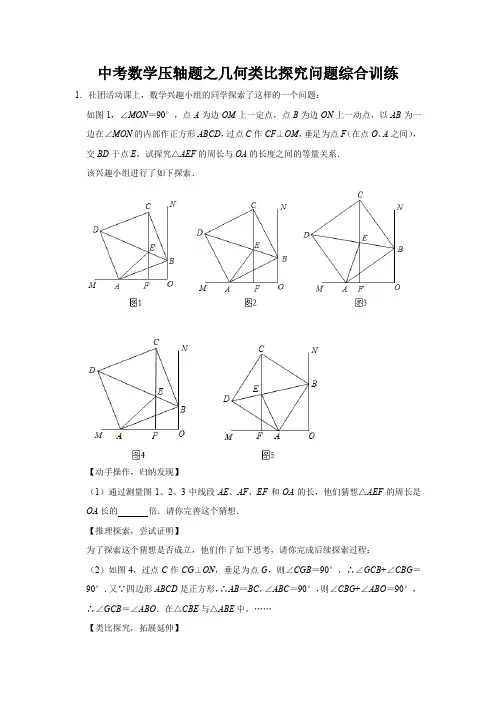
中考数学压轴题之几何类比探究问题综合训练1．社团活动课上，数学兴趣小组的同学探索了这样的一个问题：如图1，∠MON＝90°，点A为边OM上一定点，点B为边ON上一动点，以AB为一边在∠MON的内部作正方形ABCD，过点C作CF⊥OM，垂足为点F（在点O、A之间），交BD于点E，试探究△AEF的周长与OA的长度之间的等量关系．该兴趣小组进行了如下探索．【动手操作，归纳发现】（1）通过测量图1、2、3中线段AE、AF、EF和OA的长，他们猜想△AEF的周长是OA长的倍．请你完善这个猜想．【推理探索，尝试证明】为了探索这个猜想是否成立，他们作了如下思考，请你完成后续探索过程：（2）如图4，过点C作CG⊥ON，垂足为点G，则∠CGB＝90°，∴∠GCB+∠CBG＝90°．又∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝90°，则∠CBG+∠ABO＝90°，∴∠GCB＝∠ABO．在△CBE与△ABE中，……【类比探究，拓展延伸】（3）如图5，当点F在线段OA的延长线上时，直接写出线段AE、EF、AF与OA长度之间的等量关系为．2．小明遇到这样一个问题：如图1，△ABC是等边三角形，点D为BC的中点，且满足∠ADE＝60°，DE交等边△ABC外角平分线CE所在直线于点E，试探究AD与DE的数量关系．小明发现，过点D作DF∥AC，交AB于点F，通过构造全等三角形，经过推理论证，能够得到AD与DE的数量关系．（1）AD与DE相等吗？请你说明理由；【类比探究】（2）当点D是线段BC上（不与点B，C重合）任意一点时，其它条件不变，如图2，试猜想AD与DE之间的数量关系，并证明你的结论；【拓展应用】（3）当点D在BC的延长线上，且满足CD＝BC，连接AE，其它条件不变，如图3，若AD＝6，求DE的长．3．已知：Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，点P是BC边上的一个动点，（1）如图①，若点P与点D重合，连接AP，则AP与BC的位置关系是；（2）如图②，若点P在线段BD上，过点B作BE⊥AP于点E，过点C作CF⊥AP于点F，则CF，BE和EF这三条线段之间的数量关系是；（3）如图③，在（2）的条件下若BE的延长线交直线AD于点M，找出图中与CP相等的线段，并加以证明．（4）如图④，已知BC＝4，AD＝2，若点P从点B出发沿着BC向点C运动，过点B 作BE⊥AP于点E，过点C作CF⊥AP于点F，设线段BE的长度为d1，线段CF的长度为d2，试求出点P在运动的过程中d1+d2的最大值．4．如图1，△ABC为等边三角形，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转60°得到线段CN，连接BN，直线BN交射线AE 于点D．（1）直接写出直线BD与射线AE相交所成锐角的度数；（2）如图2，当射线AE与AC的夹角∠EAC为钝角时，其他条件不变，（1）中结论是否发生变化？如果不变，加以证明；如果变化，请说明理由；（3）如图3，在等腰Rt△ABC中，∠ACB＝90°，射线AE交BC于点H，∠EAC＝15°，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，连接BN，直线BN交射线AE于点D．G，F分别是AH，AB 的中点．求证：CD＝GF．5．【问题探索】如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E分别在AC、BC 边上，DC＝EC，连接DE、AE、BD，点M、N、P分别是AE、BD、AB的中点，连接PM、PN、MN．探索BE与MN的数量关系．聪明的小华推理发现PM与PN的关系为，最后推理得到BE与MN的数量关系为．【深入探究】将△DEC绕点C逆时针旋转到如图2的位置，判断（1）中的BE与MN的数量关系是否仍然成立，如果成立，请写出证明过程，若不成立，请说明理由；【解决问题】若CB＝8，CE＝2，在将图1中的△DEC绕点C逆时针旋转一周的过程中，当B、E、D三点在一条直线上时，求MN的长度．6．已知：△ABC是等腰直角三角形，∠ACB＝90°，动点P在斜边AB所在的直线上，把线段CP绕着点C逆时针旋转90°得到CQ，连接PQ，探究并解决下列问题：（1）如图1，若点P在线段AB上，请直接写出P A2，PB2，PQ2三者之间的数量关系：；（2）如图2，若点P在线段AB的延长线上，（1）中的结论是否仍然成立，若成立请给予证明；若不成立请说明理由；（3）若动点P满足＝，求的值．7．在△ABC中，CA＝CB，∠ACB＝α（0°＜α＜180°）．点P是平面内不与A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，CP．点M是AB的中点，点N是AD的中点．（1）问题发现如图1，当α＝60°时，的值是，直线MN与直线PC相交所成的较小角的度数是．（2）类比探究如图2，当α＝120°时，请写出的值及直线MN与直线PC相交所成的较小角的度数，并就图2的情形说明理由．（3）解决问题如图3，当α＝90°时，若点E是CB的中点，点P在直线ME上，请直接写出点B，P，D在同一条直线上时的值．8．如图1所示，矩形ABCD中，点E，F分别为边AB，AD的中点，将△AEF绕点A逆时针旋转α（0°＜α≤360°），直线BE、DF相交于点P．（1）若AB＝AD，将△AEF绕点A逆时针旋转至如图2所示的位置，则线段BE与DF 的数量关系是．（2）若AD＝nAB（n≠1），将△AEF绕点A逆时针旋转，则（1）中的结论是否仍然成立？若成立，请就图3所示的情况加以证明，若不成立，请写出正确结论，并说明理由．（3）若AB＝8，BC＝12，将△AEF旋转至AE⊥BE，请算出DP的长．9．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB的中点，点P为直线BC 上的动点（不与点B点C重合），连接OC、OP，将线段OP绕点P顺时针旋转60°，得到线段PQ，连接BQ．（1）观察猜想：如图①，线段BQ与CP的数量关系是；∠CBQ＝；（2）探究证明：如图②，当点P在CB的延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由．10．已知△ABC和△ADE，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，连接BD，CE．（1）如图1，当点E在AB边上时，试判断线段BD，CE之间的关系是．（2）将图1中的△ADE绕点A旋转至如图2所示位置时，探究线段BD，CE之间的关系，并说明理由；（3）将图1中的△ADE绕点A旋转至DE与直线AC垂直，直线BD交直线CE于点F，若AB＝15，AD＝5，请直接写出线段BF的长度．11．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°．（1）当点D在AC上时，如图1，试猜想线段BD和CE的数量关系是；位置关系是．（2）将图1中的△ADE绕点A顺时针旋转α角，（0°＜α＜90°），如图2，（1）中的结论是否成立，若成立，请给出证明；若不成立说明理由．12．如图1，在△ABC中，已知∠ACB＝90°，AC＝BC，点D，E分别在边AC，BC上，且CD＝CE，此时显然AD＝BE，AD⊥BE成立．若保持△ABC不动，将△DCE绕点C 逆时针旋转，旋转角为α．（Ⅰ）如图2，当0°＜α＜90°时，问：AD＝BE，AD⊥BE是否成立？若成立，请证明，若不成立，请说明理由；（Ⅱ）如图3，当α＝45°时，延长BE交AD于点F，若CE＝，BC＝3，则线段EF ＝（直接写出结果即可）．13．已知△ABC和△ADE都是等腰三角形，AB＝AC，AD＝AE．∠DAE＝∠BAC．【初步感知】（1）特殊情形：如图①．若点D，E分别在边AB，AC上，则DB EC．（填“＞”、“＜”或“＝”）（2）发现证明：如图②，将图①中的△ADE绕点A旋转，当点D在△ABC外部，点E 在△ABC内部时，求证：DB＝EC．【深入探究】（1）如图③，△ABC和△ADE都是等边三角形，点C，E，D在同一条直线上，则∠CDB 的度数为线段CE，BD之间的数量关系为；（2）如图④，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，AM为△ADE中DE边上的高．则∠CDB的度数为；线段AM．BD，CD之间的数量关系为；【拓展提升】如图⑤，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，将△ADE绕点A逆时针旋转，连接BE、CD．当AB＝5．AD＝2时，在旋转过程中，△ADE与△ADC的面积和的最大值为．14．已知△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上的一动点（点D不与点B、发现问题：如图1，当点D在边BC上时，（1）请写出BD和CE之间的位置关系为，并猜想BC和CE、CD之间的数量关系：．尝试探究：（2）如图2，当点D在边BC的延长线上且其他条件不变时，（1）中BD和CE之间的位置关系，BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；拓展延伸：（3）如图3，当点D在边CB的延长线上且其他条件不变时，若BC＝7，CE＝5，直接写出线段ED的长．15．已知△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上的一动点（点D不与点B、发现问题：如图1，当点D在边BC上时，（1）请写出BD和CE之间的位置关系为，并猜想BC和CE、CD之间的数量关系：．尝试探究：（2）如图2，当点D在边BC的延长线上且其他条件不变时，（1）中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；拓展延伸：（3）如图3，当点D在边CB的延长线上且其他条件不变时，若BC＝6，CE＝2，求线段ED的长．16．已知Rt△ABC中，AB＝AC，∠BAC＝90°，点D为直线BC上的一动点（点D不与点B、C重合），以AD为边作Rt△ADE，AD＝AE，连接CE．（1）发现问题：如图①，当点D在边BC上时，①请写出BD和CE之间的数量关系，位置关系；②线段CE、CD、BC之间的关系是；（2）尝试探究：如图②，当点D在边BC的延长线上且其他条件不变时，（1）中CE、CD、BC之间存在的数量关系是否成立？若成立，请证明；若不成立，请说明理由；（3）拓展延伸：如图③，当点D在边CB的延长线上且其他条件不变时，若BC＝4，CE＝2，求线段CD的长．17．在Rt△ABC中与Rt△DCE中，∠ACB＝∠DCE＝90°，∠BAC＝∠DEC＝30°，AC＝DC＝，将Rt△DCE绕点C顺时针旋转，连接BD，AE，点F，G分别是BD，AE的中点，连接CF，CG．（1）观察猜想如图1，当点D与点A重合时，CF与CG的数量关系是，位置关系是；（2）类比探究当点D与点A不重合时，（1）中的结论是否成立？如果成立，请仅就图2的情形给出证明；如果不成立，请说明理由．（3）问题解决在Rt△DCE旋转过程中，请直接写出△CFG的面积的最大值与最小值．18．综合与实践动手操作如图1，在Rt△ABC中，∠C＝90°，将△ABC绕点A逆时针旋转90°得到△AED．延长ED分别交CB于点F，交AB于点G，连接AF．思考探究（1）∠CAF＝°，∠EAG＝°；（2）若BC＝（+1）AC，则①∠DAG＝°；②＝，请证明你的结论；开放拓展（3）如图2，若改变旋转角，已知AC＝3，BC＝4，当∠EAF＝90°时，△AFB的面积为．19．如图，已知在△ABC和△DCE中，∠ACB＝∠DCE，且满足＝＝k，将△DEC绕点C旋转．连接BD，F，G，H分别是AB，BD，DE的中点，连接FG，GH．（1）当k＝1时，①如图（1），点D在AC边上时，判断FG，GH的数量关系是；②如图（2），点D不在AC边上时，①中的结论是否成立，并说明理由；（2）如图（3），当k＝时，探索FG，GH的数量关系．直接写出探究结论，不需证明．20．如图1，已知△ABC和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点D在线段AC上，点F为AB的中点，点M为BE的中点，点N为AD的中点．（1）如图1，请直接写出∠FMN的大小以及FM和MN之间的数量关系．（2）如图2，将△DCE绕点C顺时针旋转，此时（1）中的结论是否成立？若成立，请证明，若不成立，请写出相应正确的结论．（3）如图3，若AB＝4，CE＝2，在将△DCE绕点C顺时针旋转360°过程中，直线BD，AE交于点G，△ABG的面积的最小值为．21．在△ABC和△DEC中，∠ACB＝∠DCE＝90°，△DEC绕点C逆时针旋转，连接BD，F，G，H分别是AB，BD，DE的中点，连接FG，FH，HG．（1）如图1，当∠A＝∠EDC＝45°，点D在AC边上时，直接猜想FG，HG的数量关系和位置关系是；（2）如图2，当∠A＝∠EDC＝45°，点D不在AC边上时，（1）猜想的结论是否成立？如果成立，请证明；如果不成立，请说明理由；（3）如图3，当∠A＝∠EDC＝30°时，猜想FG，HG的数量关系和位置关系，请直接写出猜想结论．。

中考数学类比探究型几何综合题专题训练【类型1】通过位置变化（图形变换）进行类比探究〖例1〗已知：如图，等边△AOB的边长为4，点C为OA中点．（1）如图1，将OC绕点O顺时针旋转，使点C落到OB边的点D处，设旋转角为α（0°＜α≤360°）．则此时α＝；此时△COD是三角形（填特殊三角形的名称）．（2）如图2，固定等边△AOB不动，将（1）中得到的△OCD绕点O逆时针旋转，连接AC，BD，设旋转角为β（0°＜β≤360°）．①求证：AC＝BD；②当旋转角β为何值时，OC∥AB，并说明理由；③当A、C、D三点共线时，直接写出线段BD的长．〖例2〗现有与菱形有关的三幅图，如图：（1）（感知）如图①，AC是菱形ABCD的对角线，∠B＝60°，E、F分别是边BC、CD上的中点，连结AE、EF、AF．若AC＝2，则CE+CF的长为．（2）（探究）如图②，在菱形ABCD中，∠B＝60°．E是边BC上的点，连结AE，作∠EAF＝60°，边AF交边CD于点F，连结EF．若BC＝2，求CE+CF的长．（3）（应用）在菱形ABCD中，∠B＝60°．E是边BC延长线上的点，连结AE，作∠EAF＝60°，边AF交边CD延长线于点F，连结EF．若BC＝2，EF⊥BC时，借助图③求△AEF的周长．〖尝试练习〗1．如图1，等边△ABC与等边△BDE的顶点B重合，D、E分别在AB、BC上，AB＝2√2，BD＝2．现将等边△BDE从图1位置开始绕点B顺时针旋转，如图2，直线AD、CE相交于点P．（1）在等边△BDE旋转的过程中，试判断线段AD与CE的数量关系，并说明理由；（2）在等边△BDE顺时针旋转180°的过程中，当点B到直线AD的距离最大时，求PC的长；（3）在等边△BDE旋转一周的过程中，当A、D、E三点共线时，求CE的长．2．△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．（1）探究猜想如图1，当点D在线段BC上时，①BC与CF的位置关系为：；②BC、CD、CF之间的数量关系为：；（2）深入思考如图2，当点D在线段CB的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）拓展延伸如图3，当点D在线段BC的延长线上时，正方形ADEF对角线交于点O．若已知AB＝2√2，CD ＝14BC，请求出OC的长．3．如图1，正方形ABCD与正方形AEFG有公共的顶点A，且正方形AEFG的边AE，AG分别在正方形ABCD的边AB，AD上，显然BE＝DG，BE⊥DG．（1）将图1的正方形AEFG绕点A转动一定的角度到图2的位置．求证：①BE＝DG；②BE⊥DG；（2）如图3，若点D，G，E在同一条直线上，且正方形ABCD的边长是4√2，正方形AEFG的边长为3√2，求BE的长．【类型2】通过形状变化进行类比探究〖例3〗如图1，在△ABC中，AB＝AC，∠BAC＝α．D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转α，得到AE，连接DE，CE．（1）求证：CE＝BD；（2）若α＝60°，其他条件不变，如图2．请猜测线段AC，CD，CE之间的数量关系，并说明理由；（3）若α＝90°，其他条件不变，如图3，请写出∠ACE的度数及线段AD，BD，CD之间的数量关系，并说明理由．〖例4〗如图1，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且PC ＝PE，PF交CD于点F．（1）求证：∠PCD＝∠PED；（2）连接EC，求证：EC＝√2AP；（3）如图2，把正方形ABCD改成菱形ABCD，其他条件不变，当∠DAB＝60°时，请直接写出线段EC和AP的数量关系．〖尝试练习〗4．已知菱形ABCD和菱形DEFG有公共的顶点D，C点在DE上，且∠ADC＝∠EDG，连接AE，CG，如图1．（1）试猜想AE与CG有怎样的数量关系（直接写出关系，不用证明）；（2）将菱形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG．你认为（1）中的结论是否还成立？若成立，请给出证明；若不成立，请说明理由；（3）在（2）的条件下，如果∠ADC＝∠EDG＝90°，如图3，你认为AE和CG是否垂直？若垂直，请给出证明；若不垂直，请说明理由．5．已知在平行四边形ABCD中，AB≠BC，将△ABC沿直线AC翻折，点B落在点E处，AD与CE相交于点O，联结DE．（1）如图1，求证：AC∥DE；（2）如图2，如果∠B＝90°，AB＝√3，BC＝√6，求△OAC的面积；（3）如果∠B＝30°，AB＝2√3，当△AED是直角三角形时，求BC的长．6．如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF 为邻边作平行四边形ECFG．（1）求证：四边形ECFG是菱形；（2）连结BD、CG，若∠ABC＝120°，则△BDG是等边三角形吗？为什么？（3）若∠ABC＝90°，AB＝10，AD＝24，M是EF的中点，求DM的长．【自主反馈】7．如图1，△ABC是等边三角形，点D，E分别是BC，AB上的点，且BD＝AE，AD与CE交于点F．（1）求∠DFC的度数；（2）将CE绕着点C逆时针旋转120°，得到CP，连接AP，交BC于点Q．①补全图形（图2中完成）；②用等式表示线段BE与CQ的数量关系，并证明．8．已知△ABC是等腰三角形．（1）如图1，若△ABC，△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，求证：△ABD ≌△ACE；（2）如图2，若△ABC为等边三角形，将线段AC绕点A逆时针旋转90°，得到AD，连接BD，∠BAC的平分线交BD于点E，连接CE．①求∠AED的度数；②试探究线段AE、CE、BD之间的数量关系，并证明．9．在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△AED，点B、C的对应点分别是E、D．（1）如图1，当点E恰好在AC上时，求∠CDE的度数；（2）如图2，若α＝60°时，点F是边AC中点，求证：DF＝BE；（3）如图3，点B、C的坐标分别是（0，0），（0，2），点Q是线段AC上的一个动点，点M 是线段AO上的一个动点，是否存在这样的点Q、M使得△CQM为等腰三角形且△AQM为直角三角形？若存在，请直接写出满足条件的点M的坐标；若不存在，请说明理由．10．在等腰直角三角形纸片ABC中，点D是斜边AB的中点，AB＝10，点E为BC上一点，将纸片沿DE折叠，点B的对应点为点B'．（1）如图①，连接CD，则CD的长为；（2）如图②，B'E与AC交于点F，DB'∥BC．①求证：四边形BDB'E为菱形；②连接B'C，则△B'FC的形状为；（3）如图③，则△CEF的周长为．11．已知正方形ABCD，以CE为边在正方形ABCD外部作正方形CEFG，连AF，H是AF的中点，连接BH，HE．（1）如图1所示，点E在边CB上时，则BH，HE的关系为；（2）如图2所示，点E在BC延长线上，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请给出新的结论并证明．（3）如图3，点B，E，F在一条直线上，若AB＝13，CE＝5，直接写出BH的长．12．（1）操作发现：如图1，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．猜想线段GF与GC有何数量关系？并证明你的结论．（2）简单应用：在（1）中，如果AB＝4，AD＝6，求CG的长．（3）类比探究：如图2，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．13．我们知道，平行四边形的对边平行且相等，利用这一性质，可以为证明线段之间的位置关系和数量关系提供帮助．重温定理，识别图形（1）如图①，我们在探究三角形中位线DE和第三边BC的关系时，所作的辅助线为“延长DE到点F，使EF＝DE，连接CF”，此时DE与DF在同一直线上且DE＝12DF，又可证图中的四边形为平行四边形，可得BC与DF的关系是，于是推导出了“DE∥BC，DE＝12BC”．寻找图形，完成证明（2）如图②，四边形ABCD和四边形AEFG都是正方形，△BEH是等腰直角三角形，∠EBH＝90°，连接CF、CH．求证CF＝√2BE．构造图形，解决问题（3）如图③，四边形ABCD和四边形AEFG都是菱形，∠ABC＝∠AEF＝120°，连接BE、CF．直接写出CF与BE的数量关系．类比探究型几何综合题专题训练（不用相似）答案与解析〖例1〗解：（1）如图1，∵△AOB是等边三角形，∴AO＝BO＝AB，∠AOB＝60°，∵将OC绕点O顺时针旋转，使点C落到OB边的点D处，∴OC＝OD，∠COD＝∠AOB＝60°＝α，∴△COD是等边三角形，答案为：60°，等边；（2）①∵△COD是等边三角形，∴OC＝OD，∠COD＝∠AOB＝60°，∴∠AOC＝∠BOD，又∵AO＝BO，∴△AOC≌△BOD（SAS），∴AC＝BD；②如图2，当点C在点O的上方时，若OC∥AB，∴∠AOC＝∠OAB＝60°＝β，如图2﹣1，当点C在点O的下方时，若OC∥AB，∴∠ABO＝∠BOC＝60°，∴β＝360°﹣60°﹣60＝240°，综上所述：β＝60°或240°；③如图3，当点D在线段AC上时，过点O作OE⊥AC于E，∵等边△AOB的边长为4，点C为OA 中点，∴AO＝AB＝OB＝4，OC＝OD＝CD＝2，∵∠AOB＝∠COD＝60°，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD，∵OE⊥CD，OC＝OD，∴CE＝DE＝1，∴OE＝√OC2−CE2＝√3，∴AE＝√OA2−OE2＝√13，∴AC＝AE+CE＝1+√13＝BD；如图4，当点C在线段AD上时，过点O作OF⊥AD于F，同理可求DF＝CF＝1，AF＝√13，∴AC＝BD＝√13﹣1，综上所述：BD＝√13+1或√13﹣1．〖例2〗解：（1）感知：∵四边形ABCD是菱形，∴BC＝CD＝AB＝2，∵E，F分别是边BC，CD的中点，∴CE＝12BC，CF＝12CD＝1，∴CE+CF＝2．故答案为：2．（2）探究：如图，连结AC．∵四边形ABCD是菱形，∴AB＝BC，AB∥CD．∴∠B+∠BCD＝180°．∵∠B＝60°，∴△ABC是等边三角形，∠BCD＝120°．∴∠BAC＝∠ACB＝60°，AB＝AC．∴∠ACF＝∠B＝60°．∵∠EAF＝60°，∴∠BAC﹣∠CAE＝∠EAF﹣∠CAE．∴∠BAE＝∠CAF．∴△ABE≌△ACF（ASA）．∴BE＝CF．∴CE+CF＝BC＝2．（3）应用：如图所示：∵四边形ABCD是菱形，∴AB＝BC，AB∥CD．∴∠B+∠BCD＝180°．∵∠B＝60°，∴△ABC是等边三角形，∠BCD＝120°．∴∠BAC＝∠ACB＝60°，AB＝AC．∴∠CAD＝∠B＝60°．∵∠EAF＝60°，∴∠CAD﹣∠DAE＝∠EAF ﹣∠DAE．∴∠CAE＝∠DAF．∵∠ACE＝∠ADF，AC＝AD∴△ACE≌△ADF（ASA）．∴CE＝DF，AE＝AF，∵∠EAF＝60°，∴△AEF为等边三角形，∵EF⊥BC，∠ECF＝60°，∴CF＝2CE，∵CD＝BC＝2，∴CE＝2，∴EF=√CF2−CE2=2√3，∴△AEF的周长为6√3．〖尝试练习〗1．解：（1）AD＝CE，理由：∵△ABC与△BDE都是等边三角形，∴AB＝BC，BD＝BE，∠ABC＝∠DBE ＝60°，∴∠ABD ＝∠CBE ， ∴△ABD ≌△CBE （SAS ），∴AD ＝CE ；（2）如图2，过点B 作BH ⊥AD 于H ，在Rt △BHD 中，BD ＞BH ，∴当点D ，H 重合时，BD ＝BH ，∴BH ≤BD ，∴当BD ⊥AD 时，点B 到直线AD 的距离最大，∴∠EDP ＝90°﹣∠BDE ＝30°，同（1）的方法得，△ABD ≌△CBE （SAS ），∴∠BEC ＝∠BDA ＝90°，EC ＝AD ，在Rt △ABD 中，BD ＝2，AB ＝2√2， 根据勾股定理得，AD ＝√AB 2−BD 2＝2， ∴CE ＝2，∵∠BEC ＝90°，∠BED ＝60°， ∴∠DEP ＝90°﹣60°＝30°＝∠EDP ， ∴DP ＝EP ，如图2﹣1，过点P 作PQ ⊥DE 于Q ， ∴EQ ＝12DE ＝1，在Rt △EQP 中，∠PEQ ＝30°， ∴EP ＝EQ cos∠DEP ＝2√33，∴PC ＝2−2√33； （3）①当点D 在AE 上时，如图3，∴∠ADB ＝180°﹣∠BDE ＝120°，∴∠BDE ＝60°， 过点B 作BF ⊥AE 于F ，在Rt △BDF 中，∠DBF ＝30°，BD ＝2， ∴DF ＝1，BF ＝√3，在Rt △ABF 中，根据勾股定理得，AF ＝√AB 2−BF 2＝√5，AD ＝AF ﹣DF ＝√5﹣1，∴CE ＝AD ＝√5﹣1； ②当点D 在AE 的延长线上时，如图4，同①的方法得，AF ＝√5，DF ＝1，∴AD ＝AF +DF ＝√5+1，∴CE ＝AD ＝√5+1， 即满足条件的CE 的长为√5+1和√5﹣1． 2．解：（1）①正方形ADEF 中，AD ＝AF ， ∵∠BAC ＝∠DAF ＝90°，∴∠BAD ＝∠CAF ， 又∵AB=AC ，∴△DAB ≌△FAC （SAS ），∴∠ABC ＝∠ACF ，∵AB ＝AC ，∠BAC ＝90°，∴∠ABC ＝∠ACB ＝45°，∴∠ACB +∠ACF ═45°+45°＝90°， 即BC ⊥CF ；②△DAB ≌△FAC ，∴CF ＝BD ，∵BC ＝BD +CD ， ∴BC ＝CF +CD ；故答案为：BC ＝CF +CD ；（2）CF ⊥BC 成立；BC ＝CD +CF 不成立，CD ＝CF +BC ．理由如下：∵正方形ADEF 中，AD ＝AF ，∵∠BAC ＝∠DAF ＝90°，∴∠BAD ＝∠CAF ，又∵AB=AC ， ∴△DAB ≌△FAC （SAS ），∴∠ABD ＝∠ACF ， ∵∠BAC ＝90°，AB ＝AC ， ∴∠ACB ＝∠ABC ＝45°．∴∠ABD ＝180°﹣45°＝135°，∴∠BCF ＝∠ACF ﹣∠ACB ＝135°﹣45°＝90°，∴CF ⊥BC ． ∵CD ＝DB +BC ，DB ＝CF ，∴CD ＝CF +BC ．（3）过点A 作AH ⊥BC 于点H ，过点E 作EM ⊥BD 于点M ，EN ⊥CF 于点N ， ∵∠BAC ＝90°，AB ＝AC ＝2√2， ∴BC ＝4，∴CD ＝14BC ＝1，∴BD ＝5， 由（2）同理可证得△DAB ≌△FAC ，∴BC ⊥CF ，CF ＝BD ＝5，∵四边形ADEF 是正方形，∴OD ＝OF ，∵∠DCF ＝90°， ∴DF ＝√CD 2+CF 2＝√26，∴OC ＝√262．3．证明：（1）如图2，延长DG交BE于H，∵四边形ABCD，四边形AEFG是正方形，∴AB＝AD，AG＝AE，∠DAB＝∠GAE＝90°，∴∠DAG＝∠BAE，∴△DAG≌△BAE（SAS），∴BE＝DG，∠ADG＝∠ABE，∵∠C+∠CBA+∠ABE+∠BHD+∠CDH＝360°，∴90°+90°+∠ADG+∠CDH+∠BHD＝360°，∴∠BHD＝90°，∴DG⊥BE；（2）如图3，连接BD，∵正方形ABCD的边长是4√2，正方形AEFG的边长为3√2，∴BD＝√2AD＝8，GE＝√2AE＝6，∵BD2＝DE2+BE2，∴64＝（6+BE）2+BE2，∴BE＝√23﹣3．〖例3〗证明：（1）∵将线段AD绕点A逆时针旋转α，∴AD＝AE，∠DAE＝α，∴∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）∴BD＝CE；（2）AC＝CD+CE，理由如下：∵AB＝AC，∠BAC＝60°∴△ABC是等边三角形，∴AC＝BC，由（1）可知：BD＝CE，∴BC＝BD+CD＝CE+CD，∴AC＝CD+CE；（3）∠ACE＝45°，BD2+CD2＝2AD2，理由如下：∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵△BAD≌△CAE∴∠ACE＝∠ABC＝45°，∴∠BCE＝∠ACE+∠ACB＝90°，∴CE2+CD2＝DE2，∵AD＝AE，∠DAE＝90°，∴DE2＝2AD2，∴CE2+CD2＝2AD2，∴BD2+CD2＝2AD2．〖例4〗（1）证明：∵四边形ABCD是正方形，∴AD＝DC，∠ADP＝∠CDP＝45°，又∵PD=PD，∴△ADP≌△CDP（SAS），∴∠PAD＝∠PCD，AP＝CP，∵PC＝PE，∴AP＝PE，∴∠PAD＝∠PED，∴∠PCD＝∠PED；（2）证明：∵四边形ABCD是正方形，∴∠ADC＝∠EDF＝90°，由（1）知，∠PCD＝∠PED，∵∠CFP＝∠EFD（对顶角相等），∴180°﹣∠CFP﹣∠PCD＝180°﹣∠EFD﹣∠PED，即∠CPF＝∠EDF＝90°，∵PC＝PE，∴△CPE是等腰直角三角形，∴EC＝√2CP，由（1）知，AP＝CP，∴EC＝√2AP；（3）解：AP＝CE；理由如下：∵四边形ABCD是菱形，∠DAB＝60°，∴AB＝BC，∠ABP＝∠CBP ＝60°，∠BAD＝∠BCD，∠EDC＝∠DAB＝60°，又∵PB=PB，∴△ABP≌△CBP（SAS），∴PA＝PC，∠BAP＝∠BCP，∴∠DAP＝∠DCP，∵PC＝PE，∴PA＝PE，∴∠DAP＝∠AEP，∴∠DCP＝∠AEP，∵∠CFP＝∠EFD，∴180°﹣∠CFP﹣∠PCF＝180°﹣∠EFD﹣∠AEP，即∠CPF＝∠EDF＝60°，∴△EPC是等边三角形，∴PC＝EC，∴EC＝AP，〖尝试练习〗4．解：（1）AE＝CG，理由如下：∵四边形ABCD和四边形DEFG都是菱形，∴DA＝DC，DE＝DG，又∵∠ADE=∠CDG，∴△DAE≌△DCG（SAS），∴AE＝CG；（2）成立，理由如下：∵∠ADC＝∠EDG，∴∠ADC﹣∠EDC＝∠EDG﹣∠EDC，即∠ADE＝∠CDG，又∵DA＝DC，DE＝DG，∴△DAE≌△DCG（SAS），∴AE＝CG；（3）AE ⊥CG ，理由如下：延长线段AE 、GC 交于点H ，∵AD ∥BC ，∴∠CEH ＝∠DAE ， 由（2）可知，△DAE ≌△DCG ，∴∠DAE ＝∠DCG ，∴∠CEH ＝∠DCG ，∵四边形ABCD 是菱形，∠ADC ＝90°， ∴四边形ABCD 是正方形，∴∠BCD ＝90°，∴∠ECH +∠DCG ＝90°，∴∠ECH +∠CEH ＝90°，∴∠CHE ＝90°，∴AE ⊥CG ． 5．（1）证明：由折叠的性质得：△ABC ≌△△ AEC ，∴∠ACB ＝∠ACE ，BC ＝EC ，∵四边形ABCD 是平行四边形，∴AD ＝BC ，AD ∥BC ．∴EC ＝AD ，∠ACB ＝∠CAD ，∴∠ACE ＝∠CAD ，∴OA ＝OC ，∴OD ＝OE ，∴∠ODE ＝∠OED ，∵∠AOC ＝∠DOE ，∴∠CAD ＝∠ACE ＝∠OED ＝∠ODE ，∴AC ∥DE ；（2）解：∵平行四边形ABCD 中，∠B ＝90°，∴四边形ABCD 是矩形，∴∠CDO ＝90°，CD ＝AB ＝√3，AD ＝BC ＝√6，由（1）得：OA ＝OC ，设OA ＝OC ＝x ，则OD ＝√6﹣x ，在Rt △OCD 中，由勾股定理得：（√3）2+（√6﹣x ）2＝x 2，解得：x ＝3√64，∴OA ＝3√64，∴△OAC 的面积＝12OA ×CD ＝12×3√64×√3＝9√28；（3）解：分两种情况：①如图3，当∠EAD ＝90°时，延长EA 交BC 于G ，∵AD ＝BC ，BC ＝EC ，∴AD ＝EC ， ∵AD ∥BC ，∠EAD ＝90°，∴∠EGC ＝90°， ∵∠B ＝30°，AB ＝2√3，∴∠AEC ＝30°， ∴GC ＝12EC ＝12BC ，∴G 是BC 的中点， 在Rt △ABG中，BG ＝√32AB ＝3，∴BC ＝2BG ＝6；②如图4，当∠AED ＝90°时∵AD ＝BC ，BC ＝EC ，∴AD ＝EC ，由折叠的性质得：AE ＝AB ，∴AE ＝CD ，又∵AC=AC ，∴△ACE ≌△CAD （SSS ）， ∴∠ECA ＝∠DAC ，∴OA ＝OC ，∴OE ＝OD ， ∴∠OED ＝∠ODE ，∴∠AED ＝∠CDE ， ∵∠AED ＝90°，∴∠CDE ＝90°，∴AE ∥CD ， 又∵AB ∥CD ，∴B ，A ，E 在同一直线上， ∴∠BAC ＝∠EAC ＝90°， ∵Rt △ABC 中，∠B ＝30°，AB ＝2√3， ∴AC ＝√33AB ＝2，BC ＝2AC ＝4；综上所述，当△AED 是直角三角形时，BC 的长为4或6．6．证明：（1）∵AF 平分∠BAD ，∴∠BAF ＝∠DAF ，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥CD ，∴∠DAF ＝∠CEF ，∠BAF ＝∠CFE ，∴∠CEF ＝∠CFE ，∴CE ＝CF ， 又∵四边形ECFG 是平行四边形， ∴四边形ECFG 为菱形；（2）△BDG 是等边三角形，理由如下：∵四边形ABCD 是平行四边形，∴AB ∥DC ，AB ＝DC ，AD ∥BC ，∵∠ABC ＝120°，∴∠BCD ＝60°，∠BCF ＝120°，由（1）知，四边形CEGF 是菱形，∴CE ＝GE ，∠BCG ＝12∠BCF ＝60°， ∴CG ＝GE ＝CE ，∠DCG ＝120°，∵EG ∥DF ， ∴∠BEG ＝120°＝∠DCG ，∵AE 是∠BAD 的平分线，∴∠DAE ＝∠BAE ，∵AD ∥BC ， ∴∠DAE ＝∠AEB ，∴∠BAE ＝∠AEB ，∴AB ＝BE ，∴BE ＝CD ，∴△BEG ≌△DCG （SAS ），∴BG ＝DG ，∠BGE ＝∠DGC ，∴∠BGD ＝∠CGE ，∵CG ＝GE ＝CE ，∴△CEG 是等边三角形， ∴∠CGE ＝60°，∴∠BGD ＝60°，∵BG ＝DG ， ∴△BDG 是等边三角形；（3）如图2中，连接BM ，MC ，∵∠ABC ＝90°，四边形ABCD 是平行四边形，∴四边形ABCD是矩形，又由（1）可知四边形ECFG为菱形，∠ECF＝90°，∴四边形ECFG为正方形．∵∠BAF＝∠DAF，∴BE＝AB＝DC，∵M为EF中点，∴∠CEM＝∠ECM＝45°，∴∠BEM＝∠DCM＝135°，∴△BME≌△DMC（SAS），∴MB＝MD，∠DMC＝∠BME．∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，∴△BMD是等腰直角三角形．∵AB＝10，AD＝24，∴BD＝√AB2+AD2＝26，∴DM＝√22BD＝13√2．【自主反馈】7．解：（1）∵△ABC是等边三角形，∴AB＝AC＝BC，∠BAC＝∠B＝∠ACB＝60°，又∵BD=AE，∴△ABD≌△CAE（SAS），∴∠BAD＝∠ACE，∵∠BAD+∠DAC＝60°，∴∠DFC＝∠ACE+∠DAC＝60°；（2）①根据题意补全图形如图2所示：②线段BE与CQ的数量关系为：CQ＝12BE；理由如下：∵CE绕着点C逆时针旋转120°，得到CP，∴CE＝CP，∠ECP＝120°，∵∠DFC＝60°，∴AD∥CP，∴∠ADC＝∠DCP，∵△ABD≌△CAE，∴CE＝AD，∴AD＝CP，∴△ADQ≌△PCQ（AAS），∴CQ＝DQ＝12CD，∵AB＝BC，BD＝AE，∴BE＝CD，∴CQ＝12BE．8．解：（1）∵△ABC，△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，∴AB＝AC，AD＝AE，∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△ABD≌△ACE（SAS）；（2）①∵△ABC是等边三角形，∴AB＝AC，∠BAC＝60°，由旋转知，AC＝AD，∠CAD＝90°，∴AB＝AD，∠BAD＝∠BAC+∠CAD＝150°，∴∠D＝12（180°﹣∠BAD）＝15°，∵AE是∠BAC的平分线，∴∠CAE＝12∠BAC＝30°，∴∠DAE＝∠CAD+∠CAE＝120°，∴∠AED＝180°﹣∠D﹣∠DAE＝45°；②BD＝2CE+√2AE；证明：如图，∵△ABC是等边三角形，∴AB＝AC，∵AE是∠BAC的角平分线，∴∠BAE＝∠CAE，∵AE＝AE，∴△BAE≌△CAE（SAS），∴BE＝CE，过点A作AF⊥AE交DE于F，∴∠EAF＝90°，由旋转知，∠CAD＝90°，∴∠CAE＝∠DAF，由①知，∠AED＝45°，∴∠AFE＝45°＝∠AEF，∴AE＝AF，∴EF＝√2AE，∵AC＝AD，∴△ACE≌△ADF（SAS），∴DF＝CE，∴BD＝BE+EF+DF＝CE+√2AE+CE ＝2CE+√2AE．9．解：（1）∵∠ABC＝90°，∠BAC＝30°，∴∠ACB＝60°，∵△ABC绕点A顺时针旋转α得到△AED，点E恰好在AC上，∴CA＝AD，∠EAD＝∠BAC＝30°，∴∠ACD＝∠ADC＝12（180°﹣30°）＝75°，∵∠EDA＝∠ACB＝60°，∴∠CDE＝∠ADC﹣∠EDA＝15°；（2）连接BF，∵点F是边AC中点，∴BF＝AF＝12AC，∵∠BAC＝30°，∴BC＝12AC，∴∠FBA＝∠BAC＝30°，∵△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE＝∠CAD＝60°，CB ＝DE ，∠DEA ＝∠ABC ＝90°， ∴DE ＝BF ，延长BF 交AE 于点G ，则∠BGE ＝∠GBA +∠BAG ＝90°， ∴∠BGE ＝∠DEA ，∴BF ∥ED ，∴四边形BFDE 是平行四边形，∴DF ＝BE ； （3）∵点B 、C 的坐标分别是（0，0），（0，2）， ∴BC ＝2，∵∠ABC ＝90°，∠BAC ＝30°， ∴AC ＝4，AB ＝2√3，若∠QMA ＝90°，CQ ＝MQ 时，如图3，设CQ ＝QM ＝x ，∠CAB ＝30°，∴AQ ＝2x ，AM ＝√3x ， ∴AC ＝x +2x ＝3x ＝4，∴x ＝43，∴AM ＝43√3，∴BM ＝AB ﹣AM ＝2√3﹣4√33＝2√33，∴点M （2√33，0）；若∠AQM ＝90°，CQ ＝QM 时，如图4， 设CQ ＝QM ＝x ，∠CAB ＝30°， ∴AQ ＝√3x ，AM ＝2x ， ∴AC ＝x +√3x ＝4，∴x ＝2√3﹣2，∴AM ＝4√3﹣4， ∴BM ＝2√3﹣（4√3﹣4）＝4﹣2√3， ∴点M （4﹣2√3，0）；综上所述：M （2√33，0）或（4﹣2√3，0）．10．（1）解：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，AB ＝10，∴CD ＝12AB ＝5（2）①证明：由折叠的性质得：B 'D ＝BD ，B 'E ＝BE ，∠B 'DE ＝∠BDE ，∵DB '∥BC ，∴∠B 'DE ＝∠BED ，∴∠BDE ＝∠BED ，∴BD ＝BE ，∴B 'D ＝BE ，∴四边形BDB 'E 是平行四边形，又∵B 'D ＝BD ，∴四边形BDB 'E 为菱形；②解：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，∴CD ＝12AB ＝BD ， 由折叠的性质得：B 'D ＝BD ，∴CD ＝B 'D ，∴∠DCB '＝∠DB 'C ，∵∠ACB ＝90°，∴AC ⊥BC ，∵DB '∥BC ，∴DB '⊥AC ，∴∠ACB '＝90°﹣∠DB 'C ，由①得：四边形BDB 'E 为菱形， ∴AB ∥B 'E ，∵CD ⊥AB ，∴CD ⊥B 'E ， ∴∠EB 'C ＝90°﹣∠DCB '，∴∠ACB '＝∠EB 'C ， ∴FB '＝FC ，即△B 'FC 为等腰三角形；（3）解：连接B 'C ，如图③所示：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，AB ＝10，∴BC ＝√22AB ＝5√2，∠B ＝45°，CD ＝12AB ＝BD ，∠ACD ＝12∠ACB ＝45°，由折叠的性质得：B 'D ＝BD ，∠B '＝∠B ＝45°， ∴CD ＝B 'D ，∴∠DCB '＝∠DB 'C ，∴∠FCB '＝∠FB 'C ，∴CF ＝B 'F ，∴△CEF 的周长＝EF +CF +CE ＝EF +B 'F +CE ＝B 'E +CE ＝BE +CE ＝BC ＝5√2； 11．解：（1）BH ⊥HE ，BH ＝HE ；理由如下： 延长EH 交AB 于M ，如图1所示： ∵四边形ABCD 和四边形CEFG 是正方形，∴AB ∥CD ∥EF ，AB ＝BC ，CE ＝FE ，∠ABC ＝90°，∴∠AMH ＝∠FEH ，∵H 是AF 的中点，∴AH ＝FH ，∴△AMH ≌△FEH （AAS ）， ∴AM ＝FE ＝CE ，MH ＝EH ，∴BM ＝BE ，∵∠ABC＝90°，∴BH⊥HE，BH＝12ME＝HE；（2）结论仍然成立．BH⊥HE，BH＝HE．理由如下：延长EH交BA的延长线于点M，如图2所示：∵四边形ABCD是正方形，四边形EFGC是正方形，∴∠ABE＝∠BEF＝90°，AB＝BC，AB∥CD∥EF，CE＝FE，∴∠HAM＝∠HFE，∴△AHM≌△FHE（ASA），∴HM＝HE，AM＝EF＝CE，∴BM＝BE，∵∠ABE＝90°，∴BH⊥EH，BH＝12EM＝EH；（3）延长EH到M，使得MH＝EH，连接AH、BH，如图3所示：同（2）得：△AMH≌△FEH（SAS），∴AM＝FE＝CE，∠MAH＝∠EFH，∴AM∥BF，∴∠BAM+∠ABE＝180°，∴∠BAM+∠CBE＝90°，∵∠BCE+∠CBE＝90°∴∠BAM＝∠BCE，∴△ABM≌△CBE（SAS），∴BM＝BE，∠ABM＝∠CBE，∴∠MBE＝∠ABC＝90°，∵MH＝EH，∴BH⊥EH，BH＝12EM＝MH ＝EH，在Rt△CBE中，BE＝√CB2−CE2＝12，∵BH＝EH，BH⊥EH，∴BH＝√22BE＝6√2．12．解：（1）GF＝GC．理由如下：如图1，连接GE，∵E是BC的中点，∴BE＝EC，∵△ABE沿AE折叠后得到△AFE，∴BE＝EF，∴EF＝EC，∵四边形ABCD是矩形，∴∠C＝∠B＝90°，∴∠EFG＝90°，∴Rt△GFE≌Rt△GCE（HL），∴GF＝GC；（2）设GC＝x，则AG＝4+x，DG＝4﹣x，在Rt△ADG中，62+（4﹣x）2＝（4+x）2，解得x＝94．∴GC＝94；（3）（1）中的结论仍然成立．证明：如图2，连接FC，∵E是BC的中点，∴BE＝CE，∵将△ABE沿AE折叠后得到△AFE，∴BE＝EF，∠B＝∠AFE，∴EF＝EC，∴∠EFC＝∠ECF，∵矩形ABCD为平行四边形，∴∠B＝∠D，∵∠ECD＝180°﹣∠D，∠EFG＝180°﹣∠AFE＝180°﹣∠B＝180°﹣∠D，∴∠ECD＝∠EFG，∴∠GFC＝∠GFE﹣∠EFC＝∠ECG﹣∠ECF＝∠GCF，∴∠GFC＝∠GCF，∴FG＝CG；即（1）中的结论仍然成立．13．解：（1）∵AE＝CE，DE＝EF，∠AED＝∠CEF，∴△AED≌△CEF（SAS），∴AD＝CF，∠ADE＝∠F，∴BD∥CF，∵AD＝BD，∴BD＝CF，∴四边形BCFD是平行四边形，∴DF＝BC，DF∥BC，（2）证明：∵四边形ABCD是正方形∴AB＝BC，∠ABC＝90°，即∠ABE+∠CBE＝90°∵△BEH是等腰直角三角形，∴EH＝2BE＝2BH，∠BEH＝∠BHE＝45°，∠EBH＝90°，即∠CBH+∠CBE＝90°∴∠ABE＝∠CBH，∴△ABE≌△CBH（SAS），∴AE＝CH，∠AEB＝∠CHB，∴∠CHE＝∠CHB﹣∠BHE＝∠CHB﹣45°＝∠AEB﹣45°，∵四边形AEFG是正方形，∴AE＝EF，∠AEF＝90°，∴EF＝HC，∠FEH＝360°﹣∠AEF﹣∠AEB﹣∠BEH＝225°﹣∠AEB，∴∠CHE+∠FEH＝∠AEB﹣45°+225°﹣∠AEB＝180°，∴EF∥HC且EF＝HC，∴四边形EFCH是平行四边形，∴CF＝EH＝√2BE；（3）CF＝√3BE，如图，过点B作BH，使∠EBH＝120°，且BH＝BE，连接EH、CH，则∠BHE＝∠BEH＝30°，∵∠ABC＝∠EBH＝120°，∴∠ABE＝∠CBH，∵AB＝BC，BE＝BH，∴△AEB≌△CHB（SAS），∴CH＝AE＝EF，∠CHB＝∠AEB，∵∠CHE＝∠CHB﹣∠BHE＝∠AEB﹣30°，∠FEH＝360°﹣∠AEF﹣∠AEB﹣∠BEH＝210°﹣∠AEB，∴∠CHE+∠FEH＝180°，∴CH∥EF且CH＝EF，∴四边形EFCH是平行四边形，∴CF＝EH，过B作BN⊥EH于N，在△EBH中，∠EBH＝120°，BH＝BE，∴∠BEN＝30°，EH＝2EN，BE，∴EN＝√32∴EH＝√3BE，∴CF＝EH＝√3BE．。

中考数学真题分类汇编——几何综合题(含答案)类型1 类比探究的几何综合题类型2 与图形变换有关的几何综合题类型3 与动点有关的几何综合题类型4 与实际操作有关的几何综合题类型5 其他类型的几何综合题类型1 类比探究的几何综合题（2018苏州）（2018烟台）（2018东营）（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=33，BO：CO=1:3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．请回答：∠ADB= °，AB= ．（2）请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=33，∠ABC=∠ACB=75°， BO：OD=1:3，求DC的长．（2018长春）(第24题图1) (第24题图2) (第24题图3)（2018陕西）（2018齐齐哈尔）（2018河南）（2018仙桃）问题：如图①，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A 逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；探索：如图②，在Rt△ABC与Rt△ADE中，AB=AC，AD=AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；应用：如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD的长．（2018襄阳）如图(1)，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．(1)证明与推断：①求证：四边形CEGF是正方形；的值为；②推断：AGBE(2)探究与证明：将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图(2)所示，试探究线段AG与BE 之间的数量关系，并说明理由；(3)拓展与运用正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图(3)所示，延长CG交AD于点H．若AG=6，GH=22，则BC= ．（2018淮安）（2018咸宁）（2018黄石）在△ABC 中，E 、F 分别为线段AB 、AC 上的点（不与A 、B 、C 重合）. （1）如图1，若EF ∥BC ，求证：AEF ABC S AE AFS AB AC∆∆= （2）如图2，若EF 不与BC 平行，（1）中的结论是否仍然成立？请说明理由；（3）如图3，若EF 上一点G 恰为△ABC 的重心，34AE AB =,求AEFABC S S ∆∆的值.BBB（2018山西）（2018盐城）【发现】如图①，已知等边ABC ，将直角三角形的60角顶点D 任意放在BC 边上（点D 不与点B 、C 重合），使两边分别交线段AB 、AC 于点E 、F .（1）若6AB=，4AE=，2BD=，则CF=_______；（2）求证：EBD DCF∆∆.【思考】若将图①中的三角板的顶点D在BC边上移动，保持三角板与AB、AC的两个交点E、F都存在，连接EF，如图②所示.问点D是否存在某一位置，使ED平分BEF∠且FD平分CFE∠？若存在，求出BDBC的值；若不存在，请说明理由.【探索】如图③，在等腰ABC∆中，AB AC=，点O为BC边的中点，将三角形透明纸板的一个顶点放在点O处（其中MON B∠=∠），使两条边分别交边AB、AC于点E、F（点E、F均不与ABC∆的顶点重合），连接EF.设Bα∠=，则AEF∆与ABC∆的周长之比为________（用含α的表达式表示）.（2018绍兴）（2018达州）（2018菏泽）（2018扬州）问题呈现如图1，在边长为1的正方形网格中，连接格点D、N和E、C，DN与EC相交于点P，求tan CPN∠的值.方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形.观察发现问题中CPN∠不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题.比如连接格点M、N，可得∠就变换到中Rt DMN∆.∠=∠，连接DM，那么CPNMN EC，则DNM CPN//问题解决（1）直接写出图1中tan CPN ∠的值为_________；（2）如图2，在边长为1的正方形网格中，AN 与CM 相交于点P ，求cos CPN ∠的值； 思维拓展（3）如图3，AB BC ⊥，4AB BC =，点M 在AB 上，且AM BC =，延长CB 到N ，使2BN BC =，连接AN 交CM 的延长线于点P ，用上述方法构造网格求CPN ∠的度数.（2018常德）已知正方形ABCD 中AC 与BD 交于O 点，点M 在线段BD 上，作直线AM 交直线DC 于E ,过D 作DH AE ⊥于H ,设直线DH 交AC 于N .（1）如图14，当M 在线段BO 上时，求证：MO NO =；（2）如图15，当M 在线段OD 上，连接NE ,当//EN BD 时，求证：BM AB =； （3）在图16，当M 在线段OD 上，连接NE ,当NE EC ⊥时，求证：2AN NC AC =⋅.（2018滨州）（2018湖州）（2018自贡）如图，已知AOB 60∠=,在AOB ∠的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合，它的两条边分别与直线OA OB 、相交于点D E 、 .⑴当DCE ∠绕点C 旋转到CD 与OA 垂直时（如图1），请猜想OE OD +与OC 的数量关系，并说明理由；⑵当DCE ∠绕点C 旋转到CD 与OA 不垂直时，到达图2的位置，⑴中的结论是否成立？并说明理由； ⑶当DCE ∠绕点C 旋转到CD 与OA 的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD OE 、与OC 之间又有怎样的数量关系？请写出你的猜想，不需证明.（2018嘉兴、舟山）O BOO B图3.（2018淄博）（1）操作发现：如图①，小明画了一个等腰三角形ABC ，其中AB AC =，在ABC ∆的外侧分别以,AB AC 为腰作了两个等腰直角三角形ABD ACE ，，分别取,BD CE ，BC 的中点,,M N G ，连接,GM GN .小明发现了：线段GM 与GN 的数量关系是 ；位置关系是 . （2）类比思考：如图②，小明在此基础上进行了深入思考.把等腰三角形ABC 换为一般的锐角三角形，其中AB AC >，其它条件不变，小明发现的上述结论还成立吗？请说明理由. （3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究.向ABC ∆的内侧分别作等腰直角三角形,ABD ACE ，其它条件不变，试判断GMN ∆的形状，并给与证明.类型2 与图形变换有关的几何综合题（2018宜昌）在矩形ABCD 中，12AB =，P 是边AB 上一点，把PBC 沿直线PC 折叠，顶点B 的对应点是点G ，过点B 作BE CG ⊥，垂足为E 且在AD 上，BE 交PC 于点F . (1)如图1，若点E 是AD 的中点，求证:AEB DEC ∆∆≌； (2) 如图2，①求证: BP BF =；②当AD 25=，且AE DE <时，求cos PCB ∠的值； ③当BP 9=时，求BE EF 的值.图1 图2 图2备用图 23.(1)证明：在矩形ABCD 中，90,A D AB DC ∠=∠==, 如图1，又AE DE =，图1∆≅∆,ABE DCE(2)如图2，图2①在矩形ABCD中，90∠=,ABC∆沿PC折叠得到GPC∆BPC∠=∠∴∠=∠=,BPC GPC PGC PBC90⊥BE CG∴,BE PG//∴∠=∠GPF PFBBPF BFP∴∠=∠∴=BP BFAD=时，②当25∠=BEC90∴∠+∠=,90AEB CED90AEB ABE ∠+∠=,CED ABE ∴∠=∠ 又90A D ∠=∠=,ABE DEC ∴∆∆∽AB DEAE CD∴=∴设AE x =，则25DE x =-，122512xx -∴=， 解得19x =，216x =AE DE <9,16AE DE ∴==, 20,15CE BE ∴==,由折叠得BP PG =，BP BF PG ∴==,//BE PG , ECF GCP ∴∆∆∽EF CEPG CG∴=设BP BF PG y ===，152025y y -∴=253y ∴=则253BP = 在Rt PBC ∆中，PC =,cos 10BC PCB PC ∠=== ③若9BP =,解法一：连接GF ，（如图3）90GEF BAE ∠=∠=, //,BF PG BF PG =∴四边形BPGF 是平行四边形BP BF =,∴平行四边形BPGF 是菱形//BP GF ∴, GFE ABE ∴∠=∠, GEF EAB ∴∆∆∽EF ABGF BE∴=129108BE EF AB GF ∴==⨯= 解法二：如图2，90FEC PBC ∠=∠=,EFC PFB BPF ∠=∠=∠, EFC BPC ∴∆∆∽EF CEBP CB∴=又90BEC A ∠=∠=, 由//AD BC 得AEB EBC ∠=∠,AEB EBC ∴∆∆∽AB CEBE CB∴=AE EFBE BP∴=129108BE EF AE BP ∴==⨯=解法三：（如图4）过点F 作FH BC ⊥，垂足为HBPF PFEGS BF BFS EF PG BE∆==+四边形图41212BFC BEC S BF EF BC EFBE S BC ∆∆⋅===⨯ 912EFBE ∴=129108BE EF ∴=⨯=（2018邵阳）（2018永州）（2018无锡）（2018包头）（2018赤峰）（2018昆明）（2018岳阳）（2018宿迁）（2018绵阳）（2018南充）（2018徐州）类型3 与动点有关的几何综合题（2018吉林）（2018黑龙江龙东）（2018黑龙江龙东）（2018广东）已知Rt△OAB，∠OAB=90o，∠ABO=30o，斜边OB=4，将Rt△OAB绕点O顺时针旋转60o，如图25-1图，连接BC.（1）填空：∠OBC=_______o；（2）如图25-1图，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图25-2图，点M、N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒.设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？（结果可保留根号）（2018衡阳）（2018黔东南）如图1，已知矩形AOCB，6cm s的AB cm=，动点P从点A出发，以3/=，16BC cm速度向点O运动，直到点O为止；动点Q同时从点C出发，以2/cm s的速度向点B运动，与点P同时结束运动.（1）点P 到达终点O 的运动时间是________s ，此时点Q 的运动距离是________cm ； （2）当运动时间为2s 时，P 、Q 两点的距离为________cm ； （3）请你计算出发多久时，点P 和点Q 之间的距离是10cm ；（4）如图2，以点O 为坐标原点，OC 所在直线为x 轴，OA 所在直线为y 轴，1cm 长为单位长度建立平面直角坐标系，连结AC ，与PQ 相交于点D ，若双曲线ky x=过点D ，问k 的值是否会变化？若会变化，说明理由；若不会变化，请求出k 的值.（2018青岛）已知：如图，四边形ABCD ，//,AB DC CB AB ⊥，16,6,8AB cm BC cm CD cm ===，动点P 从点D 开始沿DA 边匀速运动，动点Q 从点A 开始沿AB 边匀速运动，它们的运动速度均为2/cm s .点P 和点Q 同时出发，以QA QP 、为边作平行四边形AQPE ，设运动的时间为()t s ，05t <<.根据题意解答下列问题： （1）用含t 的代数式表示AP ；（2）设四边形CPQB 的面积为()2S cm ，求S 与t 的函数关系式； （3）当QP BD ⊥时，求t 的值；（4）在运动过程中，是否存在某一时刻t ，使点E 在ABD ∠的平分线上？若存在，求出t 的值；若不存在，请说明理由.（2018广州）如图12，在四边形ABCD 中，∠B=60°，∠D=30°，AB=BC. (1)求∠A+∠C 的度数（2）连接BD,探究AD,BD,CD 三者之间的数量关系，并说明理由。

专项训练（一）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）如图所示，现有一张边长为4的正方形纸片ABCD ，点P 为正方形AD 边上的一点（不与点A ，点D 重合），将正方形纸片折叠，使点B 落在P 处，点C 落在G 处，PG 交DC 于H ，折痕为EF ，连接BP ，BH ． （1）求证：∠APB =∠BPH ．（2）当点P 在边AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论．（3）设AP 为x ，四边形EFGP 的面积为S ，求出S 与x 的函数关系式，试问S 是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．（备用图）A EBPDH GFCCFGH DPBEA备用图专项训练（二）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）数学课上，魏老师出示图1和下面框中条件：图1 图2（1）①当点C 与点F 重合时，如图2所示，可得AMDM的值为___________； ②在平移过程中，AMDM的值为___________（用含x 的代数式表示）． （2）将图2中的三角板ABC 绕点C 逆时针旋转，原题中的其他条件保持不变．当点A 落在线段DF 上时，如图3所示，请计算AMDM的值． （3）将图1中的三角板ABC 绕点C 逆时针旋转m 度，090m ≤，原题中的其他条件保持不变，如图4所示，请计算AMDM的值（用含x 的代数式表示）．图3 图4如图1，两块等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上，∠ABC =∠DEF =90°，AB =1，DE =2．将直线EB 绕点E 逆时针旋转45°，交直线AD 于点M ．将图1中的三角板ABC 沿直线l 向右平移，设C ，E 两点间的距离为x ．专项训练（三）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）已知：线段OA ⊥OB ，点C 为OB 中点，D 为线段OA 上一点．连接AC ，BD 交于点P ．（1）如图1，当OA =OB ，且D 为OA 中点时，求APPC的值； （2）如图2，当OA =OB ，且14AD OA 时，求tan ∠BPC 的值； （3）如图3，当AD :OA :OB =1:n:tan ∠BPC 的值．A OCBDPA BPCDO O DCPBA图1 图2 图3专项训练（四）做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日22.（10分）如图，在矩形ABCD中，点M是AD的中点，AD=CD=，直角∠PME绕点M进行旋转，其两边分别和BC，CD交于点P和点E，连接PE交MC于点Q．（1）判断线段MP，ME的数量关系，并进行证明；（2）当动点P，E分别在线段BC和CD上运动时，设PC=x，MQ=y，求y 与x的函数关系式；（3）在（2）中，当y取最小值时，判断PE与BM的位置关系，并说明理由．PQE M DCB A专项训练（五）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）如图，在平行四边形ABCD 中，AB =5，BC =10，F 为AD 的中点，CE ⊥AB 于E ，设∠ABC =α（60°≤α<90°）． （1）当α=60°时，求CE 的长． （2）当60°<α<90°时，①是否存在正整数k ，使得∠EFD =k ∠AEF ？若存在，求出k 的值；若不存在，请说明理由．②连接CF ，当CE 2 CF 2取最大值时，求tan ∠DCF 的值．FDCBEA专项训练（六）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）点A ，B 分别是两条平行线m ，n 上任意一点，在直线n 上找一点C ，使BC =kAB ，连接AC ，在线段AC 上任取一点E ，作∠BEF =∠ABC ，EF 交直线m 于点F ．（1）如图1，当∠ABC =90°，k =1时，判断线段EF 和EB 之间的数量关系，并证明．（2）如图2，当∠ABC =90°，k ≠1时，（1）中结论还成立吗？若成立，请证明；若不成立，请重新判断线段EF 和EB 之间的数量关系．（3）如图3，当0°<∠ABC <90°，k =1时，探究EF 和EB 之间的数量关系，并证明．mnAF CB Emn A F E CBB CEF A图1 图2 图3专项训练（七）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）如图1，在等腰Rt △ABC 和等腰Rt △CDE （CD >BC ）中，点C ，B ，D 在同一直线上，点M 是AE 的中点．（1）探究线段MD ，MB 的位置及数量关系，并证明．（2）将图1中的△CDE 绕点C 顺时针旋转45°，使△CDE 的斜边CE 恰好与△ABC 的边BC 垂直，如图2，原问题中的其他条件不变，则（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．（3）若将图2中的△ABC 绕点C 逆时针旋转大于0°且小于45°的角，如图3，原问题中的其他条件不变，则（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．EMDC BA图1EM DBA图2ABCDM图3专项训练（八）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）如图1，四边形ABCD 是正方形，点E 是边BC 的中点．∠AEF =90°，且EF 交正方形外角∠DCG 的平分线CF 于点F ． （1）求证：AE =EF ．（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上除B ，C 外的任意一点”，其他条件不变，那么结论“AE =EF ”仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由．（3）如图3，点E 是BC 延长线上除C 点外的任意一点，其他条件不变，结论“AE =EF ”仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由．GAB C DFE图1E FDC B AG图2FDBAG图3专项训练（九）做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日22.（10分）问题背景（1）如图1，△ABC中，DE∥BC，分别交AB，AC于D，E两点，过点E 作EF∥AB，交BC于点F．请按图示数据填空：四边形DBFE的面积S=_________，△EFC的面积S1=_________，△ADE 的面积S2=__________．专项训练（十）做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日22. （10分）如图，在△ABC 中，AB =AC =10厘米，BC =12厘米，D 是BC 的中点，点P 从B 出发，以a 厘米/秒（a >0）的速度沿BA 匀速向点A 运动，点Q 同时以1厘米/秒的速度从D 出发，沿DB 匀速向点B 运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为t 秒．P D BA专项训练（十一）做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日22.（10分）如图，在Rt△ABC中，∠C=90°，AB=25cm，AC=20cm．点P从点A出发，沿AB的方向匀速运动，速度为5cm/s；同时点M从点C出发，沿CA的方向匀速运动，速度为4cm/s．过点M作MN∥AB，交BC于点N．设运动的时间为t秒（0<t<5）．（1）用含t的代数式表示线段MN的长．（2）连接PN，是否存在某一时刻t，使得四边形AMNP为菱形？若存在，求出此时t的值；若不存在，请说明理由．（3）连接PM，PN，是否存在某一时刻t，使得点P在线段MN的垂直平分线上？若存在，求出此时t的值；若不存在，请说明理由．AC （备用图）（ABC专项训练（十二）做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日参考答案22．（1）证明略；（2）△PDH 的周长不发生变化，证明略； （3）21282S x x =-+，当x =2时，S 存在最小值，最小值为6．中考数学动态几何、类比探究专项训练（二）参考答案22．（1）①1；②2x； （2）1AMDM =； （3）2AM x DM =．中考数学动态几何、类比探究专项训练（三）参考答案22．（1）APPC=2； （2）tan ∠BPC 12=；（3）tan ∠BPC =．中考数学动态几何、类比探究专项训练（四）参考答案22．（1）MP =ME ，证明略；（2）2144y x =+；（3）当y 取最小值时，PE ∥BM ，理由略．参考答案22．（1）CE=．．（2）①存在，k=3；②tan∠DCF3中考数学动态几何、类比探究专项训练（六）参考答案22．（1）EF=EB，证明略；（2）不成立，此时EB=kEF；（3）EF=EB，证明略．中考数学动态几何、类比探究专项训练（七）参考答案22．（1）MD⊥MB，MD=MB，证明略；（2）不发生变化，证明略；（3）不发生变化，证明略．中考数学动态几何、类比探究专项训练（八）参考答案22．（1）证明略；（2）结论仍成立，证明略；（3）结论仍成立，证明略．中考数学动态几何、类比探究专项训练（九）参考答案22．（1）6，9，1；（2）证明略；（3）18．参考答案22．（1）1813t=；（2）①PQ154=厘米；②不存在，理由略．中考数学动态几何、类比探究专项训练（十一）参考答案22．（1）MN=5t；（2）存在，209t=；（3）存在，16057t=．中考数学动态几何、类比探究专项训练（十二）参考答案22．（1）BC=10；（2）5017t=；（3）102560 3817或或．。

初中数学相似之类比探究综合测试卷一、单选题(共3道，每道30分)1.如图(1),正方形AEGH的顶点E,H在正方形ABCD的边上,则HD:GC:EB的结果是( )A.2:3:2B.1:1:1C.2:6:3D.答案：D试题难度：三颗星知识点：相似之类比探究2.尝试探究:将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),请探究HD:GC:EB的值.解题思路:首先,可证△ADH≌△ABE,则HD:EB=________;其次,连接AC、AG,则△AGC和△AEB 的关系是__________,则GC:EB=________;最后,HD:GC:EB=______________.以上横线处,依次所填正确的是( )①1:1;②;③全等;④相似;⑤3:2;⑥;⑦2:6:3;⑧;A.①;④;⑥;⑧B.①;③;⑤;⑧C.②;④;⑥;⑧D.②;③;⑥;⑦答案：A试题难度：三颗星知识点：相似之类比探究3.类比延伸:把图(2)中的正方形都换成矩形,如图(3),且DA:AB=HA:AE=m:n,请探究HD:GC:EB的值.解题思路:类比第2题,可证△ADH和△ABE的关系是________,则HD:EB=________;其次,连接AC,AG,则△ABC和△AEG的关系是__________,则△AGC和△AEB的关系是__________,则GC:EB=________;最后,HD:GC:EB=______________.以上横线处,依次所填正确的是( )①相似;②全等;③m:n;④n:m;⑤;⑥;⑦;⑧A.①;③;①;①;⑥;⑧B.①;③;①;①;⑥;⑦C.①;④;①;①;⑤;⑧D.②;③;①;①;⑥;⑧答案：B试题难度：三颗星知识点：相似之类比探究。

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合___________________先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找______________．结合所求目标，依据_____________，大胆猜测、尝试、验证问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？类比探究综合测试（二）一、单选题(共6道，每道16分)1.如图1，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．（1）若BD=CD，CF=2AF，则的值为( )A.2B.C. D.2.（上接第1题）（2）如图2，若BD=CD，CF=mAF，则的值为( )（用含m的代数式表示）A. B.C. D.3.（上接第1，2题）（3）如图3，将原题改为“过点D的一条直线交AC的延长线于点F，交AB于点E”，若BD=nCD，CF=mAF，则的值为( )（用含m，n的代数式表示）A. B.C. D.4.类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°，则∠C 的度数为( )（1）∠C的度数为( )A.70°B.130°C.80°D.30°5.（上接第4题）（2）在探究“等对角四边形”性质时，小红画了一个“等对角四边形”ABCD （如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．那么小红的发现是正确的吗？猜想是正确的吗？( )A.小红的发现是正确的，猜想也是正确的B.小红的发现是正确的，猜想是错误的C.小红的发现是错误的，猜想也是错误的D.小红的发现是错误的，猜想是正确的6.（上接第4，5题）（3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．则对角线AC的长为( )A. B.C. D.。