2020河南中考数学复习专题专题 类比探究题.pptx
- 格式:pptx
- 大小:281.18 KB
- 文档页数:25
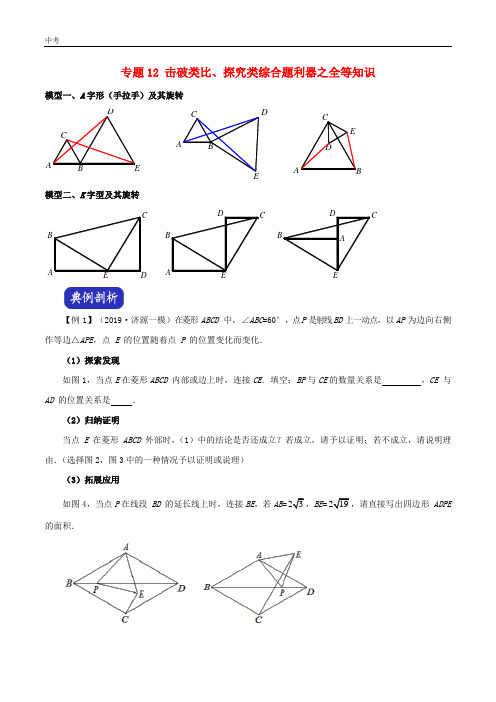
专题12 击破类比、探究类综合题利器之全等知识模型一、A字形(手拉手)及其旋转A BCDEA BC DEA BCDE模型二、K字型及其旋转AD CEBD CEB AA DCEB【例1】(2019·济源一模)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.(1)探索发现如图1,当点E在菱形ABCD内部或边上时,连接CE.填空:BP与CE的数量关系是,CE与AD的位置关系是.(2)归纳证明当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.(选择图2,图3中的一种情况予以证明或说理)(3)拓展应用如图4,当点P在线段BD的延长线上时,连接BE,若AB=23,BE=219,请直接写出四边形ADPE 的面积.图1 图2图3 图4 【答案】(1)BP=CE,CE⊥AD;(2)(3)见解析.【解析】解:(1)连接AC,延长CE至AD,∵四边形ABCD是菱形,∠ABC=60°,∴∠BAD=120°,∴∠BAC=60°,∠CAD=60°,∴△ABC是等边三角形,∴AB=AC,∵△APE是等边三角形,∴AP=AE,∠PAE=60°,∴∠BAP=∠CAE,∴△BAP≌△CAE,∴BP=CE,∵∠ABC=60°,∴∠ABP=30°,∵△BAP≌△CAE,∴∠ABP=∠ACE=30°,∵∠CAD=60°,∴∠ACE+∠CAD=90°,即CD⊥AD.(2)结论仍然成立,理由如下:(以图2为例)连接AC,设CE与AD交于点H,∵四边形ABCD是菱形,∠ABC=60°,∴△ABC和△ACD是等边三角形,∠ABD=∠CBD=30°,∴AB=AC,∠BAC=60°,∵△APE是等边三角形,∴AP=AE,∠PAE=60°,∴∠BAP=∠CAE,∴△BAP≌△CAE,∴BP=CE,∠ACE=∠ABP=30°,∵∠CAH=60°,∴∠AHC=90°,即CE⊥AD;(3)连接AC交BD于O,连接CE,由(2)知,CE⊥BC,∵AB=23BE=19在Rt△BCF中,由勾股定理得:CE=8,由△BAP≌△CAE,得:BP=CE,BD=6,∴DP=BP-BD=2,AO,在Rt△AOP中,由勾股定理得:AP=∴S=S△ADP+S△APE=(2122⨯【变式1-1】(2019·周口二模)在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.(1)如图1,图2,若△ABC为等腰直角三角形,问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是_____________,数量关系是______________;深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;类比拓展:(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=,当BM=_________时,BP的最大值为__________.图1CBMNBC图2图3CBA MNP图1 图2 图3【答案】(1)BN⊥AM,BN=AM;(2)见解析,(3)2, 1.【解析】解:(1)由AC=BC,∠ACM=∠BCN,CM=CN,可证△ACM≌△BCN,∴BN=AM,∠A=∠CBN=45°,∴∠ABN=90°,即BN⊥AM.(2)BN ⊥AM ,BN =AM ;理由如下:A∵△ABC 是等腰直角三角形,∴AC =BC ,∠A =∠ABC =45°,∠ACB =90°, 同理,∠NCM =90°,NC =MC , ∴∠ACM =∠BCN , ∴△ACM ≌△BCN ,∴BN =AM ,∠A =∠CBN =45°, ∴∠ABN =90°,即BN ⊥AM .(3)过C 作CG ⊥BC 交BA 的延长线于G ,过C 作CH ⊥AB 于H ,如图所示,G易证△GCM ≌△BCN , 由(2)知,BN ⊥AB , ∴△CHM ∽△MBP ,∴CH HMBM BP =, 即44BM BM BP-=, 设BM =x , 则BP =()21214x -+, ∴当BM =2时,BP 取最小值,最小值为1.【例2】(2018·洛阳三模)在正方形ABCD中,动点E、F分别从D、C两点出发,以相同的速度在直线DC,CB上移动.(1)如图1,当点E在边CD上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理由;(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,请你直接写出△ACE为等腰三角形时CE:CD的值;(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.【答案】见解析.【解析】解:(1)AE=DF,AE⊥DF,理由如下:∵四边形ABCD是正方形,∴AD=DC,∠ADE=∠DCF=90°,由题意知:DE=CF,∴△ADE≌△DCF,∴AE=DF,∠DAE=∠FDC,∵∠ADE=90°,∴∠ADP+∠CDF=90°,∴∠ADP+∠DAE=90°,∴∠APD=180°﹣90°=90°,∴AE⊥DF;(2)(1)中的结论还成立,CE:CD2或2,理由如下:①如图,当AC=CE时,设正方形ABCD的边长为a,由勾股定理得:AC=CE=2a,则CE:CD=2a:a=2;②如图,当AE=AC时,设正方形ABCD的边长为a,由勾股定理得:AC=AE=2a,∵四边形ABCD是正方形,∴∠ADC=90°,即AD⊥CE,∴DE=CD=a,∴CE:CD=2a:a=2;故,CE:CD=2或2;(3)∵点P在运动中∠APD=90°,∴点P的路径是以AD为直径的圆,如图,设AD的中点为Q,连接CQ并延长交圆Q于点P,此时CP的长度最大,在Rt△QDC中,由勾股定理得:QC=5,∴CP=QC+QP=5+1,即线段CP的最大值是5+1.【变式2-1】(2019·西华县一模)如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的数量关系是,位置关系是;(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.图1 图2 图3【答案】(1)FG=CE,FG∥CE;(2)(3)见解析.【解析】解:(1)FG=CE,FG∥CE;∵BF=CE,BC=CD,∠FBC=∠DCE=90°,∴△BCF≌△CDE,∴∠DEC=∠CFB,∵∠CFB+∠FCB=90°,∴∠DEC+∠FCB=90°,即CF⊥DE,∵DE⊥EG,∴EG∥CF,∴EG=DE=CF,∴四边形FCEG是平行四边形,∴FG=CE,FG∥CE;(2)∵BF=CE,BC=CD,∠FBC=∠DCE=90°,∴△BCF≌△CDE,∴∠DEC=∠CFB,CF=DE,∵∠CFB+∠FCB=90°,∴∠DEC+∠FCB=90°,即CF⊥DE,∵DE⊥EG,∴EG∥CF,∴EG=DE=CF,∴四边形FCEG是平行四边形,∴FG=CE,FG∥CE;(3)成立.由上可证:△CBF≌△DCE,得:∠BCF=∠CDE,CF=DE,∵EG=DE,∴CF=EG,∵DE⊥EG∴∠DEC+∠CEG=90°∵∠CDE+∠DEC=90°∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.1.(2019·河南南阳一模)我们定义:如图1,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB’,把AC绕点A逆时针旋转β得到AC’,连接B’C’,当α+β=180°时,我们称△AB’C’是△ABC的“旋补三角形”,△AB’C’边B’C’上的中线AD是△ABC的旋补中线,点A叫旋补中心.特例感知:(1)在图2,图3中,△AB’C’是△ABC的“旋补三角形”,△AB’C’边B’C’上的中线AD是△ABC 的旋补中线,①如图2,当△ABC是等边三角形时,AD与BC的数量关系是②如图3,当∠BAC=90°,BC=8时,则AD的长为猜想论证:(2)如图1,当△ABC是任意三角形时,猜想AD与BC的数量关系,并给予证明.【分析】(1)①由△ABC是等边三角形,得AB=BC=AC=AB’=AC’,∠BAC=60°,∠BAC+∠B’AC’=180°,得∠B’=∠C’=30°,即BC=2AD;②可利用“直角三角形中,斜边的中线等于斜边的一半”,证得:BC=2AD,AD=4;(2)BC=2AD,利用倍长中线构造全等三角形,延长AD至M使DM=AD,连接B’M,C’M,证得△ABC≌△B’AM,得BC=AM,BC=2AD.【解析】解:(1)①∵△ABC是等边三角形,∴AB=BC=AC=AB’=AC’,∠BAC=60°,∵DB’=DC’,∴AD⊥B’C’,∵BAC+∠B’AC’=180°,∴∠B’AC’=120°,∴∠B’=∠C’=30°,∴BC=2AD,即:答案为BC=2AD.②∵∠BAC=90°,BAC+∠B’AC’=180°,∴∠B’AC’=∠BAC=90°∵AB=AB’,AC=AC’,∴△BAC≌△B’AC’,∴BC=B’C’,∵B’D=DC’,∴BC=2AD,∵BC=8,∴AD=4;(2)结论:BC=2AD,理由如下:如图,延长长AD至M使DM=AD,连接B’M,C’M,∵AD=DM,B’D=DC’,∴四边形AC’MB’是平行四边形,∴AC’=B’M=AC,∵∠BAC+∠B’AC’=180°,∠AB’M+∠B’AC’=180°,∴∠BAC=∠AB’M,∵AB=AB’,∴△BAC≌△AB’M,∴BC=AM,即BC=2AD.2.(2019·郑州外国语测试)已知如图1所示,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,DE⊥AB 交BC于E,点F是AE的中点,(1)写出线段FD与线段FC的关系并证明;(2)如图2所示,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC 的关系是否变化,写出结论并证明;(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=22,直接写出线段BF的范围.【答案】见解析.【解析】解:(1)FD=FC,FD⊥FC,理由如下:由题意知:∠ADE=∠ACE=90°,AF=EF,∴DF=AF=EF=CF,∴∠FAD=∠FDA,∠FAC=∠FCA,∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=2∠FAC,∵CA=CB,∠ACB=90°,∴∠BAC=∠B=45°,∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,∴FD=FC,FD⊥FC.(2)结论不变,理由如下:延长AC至M使得CM=AC,延长ED至N,使DN=DE,连接BN、BM、EM、AN,延长ME交AN于H,交AB于O,如图所示,∵BC⊥AM,AC=CM,∴AB=BM,同理得:BE=BN,∵∠ABM=∠EBN,∠NBA=∠EBM,∴△ABN≌△MBE,∴AN=EM,∠BAN=∠BME,∵AF=FE,AC=CM,∴CF=12EM,CF∥EM,同理,FD=12AN,FD∥AN,∴FD=FC,∵∠BME+∠BOM=90°,∠BOM=∠AOH,∴∠BAN+∠AOH=90°,∴∠AHO=90°,即AN⊥MH,∴FD⊥FC.(3)由题意知,当点E落在线段AB上时,BF的长最大,如图所示,此时BF=32,当点E落在AB的延长线上时,BF的长最小,如图所示,此时,BF2,2≤BF2.3.(2019·偃师一模)特殊:(1)如图 1,在等腰直角三角形ABC中,∠ACB=90°.作CM平分∠ACB 交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD,BE.填空:①线段BD,BE的数量关系为;②线段BC,DE的位置关系为.一般:(2)如图 2,在等腰三角形ABC中,∠ACB=α,作CM平分∠ACB交AB于点M,点D为△ABC 外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE,BD,BE.请判断(1)中的结论是否成立,请说明理由.特殊:(3)如图 3,在等边三角形 ABC 中,作 BM 平分∠ABC 交 AC 于点 M ,点 D 为射线 BM 上一点,以点 B 为旋转中心将线段 BD 逆时针旋转 60°得到线段 BE ,连接 DE 交射线 BA 于点 F ,连接 AD ,AE .若 AB =4,当△ADM 与△AFD 全等时,请直接写出 DE 的值.图1 图2图3【答案】(1)BD =BE ,BC ⊥DE ;(2)(3)见解析.【解析】解:(1)由题意知:∠ACM =∠BCM =45°,由旋转知,∠DCE =90°,CD =CE ,∴∠ECB =∠DCB =45°,∵BC =BC ,∴△BCD ≌△BCE ,∴BD =BE ,∵CD =CE ,∴BC 是线段DE 的垂直平分线,∴BC ⊥DE ,(2)成立,理由如下,∵CM 平分∠ACB ,∠ACB =α,∴∠ACM =∠BCM =2α,由旋转知,∠DCE =α,CD =CE ,∴∠BCD =∠BCE =2α又∵BC =BC ,∴△BCD ≌△BCE ,∴BD =BE ,∴BC 是线段DE 的垂直平分线,∴BC ⊥DE .(3)①如图3,可证得:∠ABE =∠ABD =30°,AB ⊥DE ,由△ADM ≌△ADF ,得:∠FAD =∠MAD =30°,∴AF =BF =2,∴DE =2DF ,在Rt △ADF 中,DF =AF ·tan ∠DAF即DE=3. ②如下图所示,BD同理,得∠FBD=30°,AB =AD =4,∠ADF =∠ADM=30°,∴DE =2DF综上所述,DE 的长为:3,4.(2019·省实验一模)观察猜想(1)如图①,在Rt △ABC 中,∠BAC =90°,AB =AC =3,点D 与点A 重合,点E 在边BC 上,连接DE ,将线段DE 绕点D 顺时针旋转90°得到线段DF ,连接BF ,BE 与BF 的位置关系是 ,BE +BF = ;探究证明(2)在(1)中,如果将点D 沿AB 方向移动,使AD =1,其余条件不变,如图②,判断BE 与BF 的位置关系,并求BE +BF 的值,请写出你的理由或计算过程;(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE 绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.图1 图2 图3【答案】(1)BF⊥BE;BC;(2)(3)见解析.【解析】解:(1)∵∠EAF=∠BAC=90°,∴∠EAF-∠BAE=∠BAC-∠BAE,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为: BF⊥BE,BC.(2)过D作DH∥AC交BC于H,∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可证得:BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD =DH =2,∴BH =22,∴BF +BE =BH =22;(3)过D 作DH ∥AC 交BC 的延长线于H ,作DM ⊥BC 于M .∵AC ∥DH ,∴∠ACH =∠H ,∠BDH =∠BAC =α,∵AB =AC ,∴∠ABC =∠ACB∴∠DBH =∠H ,∴DB =DH ,∵∠EDF =∠BDH =α,∴∠BDF =∠HDE ,∵DF =DE ,DB =DH ,∴△BDF ≌△HDE ,∴BF =EH ,∴BF +BE =EH +BE =BH ,∵DB =DH ,DM ⊥BH ,∴BM =MH ,∠BDM =∠HDM ,∴BM =MH =BD •sin 2α.∴BF +BE =BH =2n •sin 2α.5.(2019·濮阳二模)在△ABC 中,AC =BC ,∠ACB =α,点D 为直线BC 上一动点,过点D 作DF ∥AC 交AB 于点F ,将AD 绕点D 顺时针旋转α得到ED ,连接BE .(1)特例猜想如图1,当α=90°时,试猜想:①AF与BE的数量关系是;②∠ABE=;(2)拓展探究如图(2),当0°<α<90°时,请判断AF与BE的数量关系及∠ABE的度数,并说明理由.(3)解决问题如图(3),在△ABC中,AC=BC,AB=8,∠ACB=α,点D在射线BC上,将AD绕点D顺时针旋转α得到ED,连接BE,当BD=3CD时,请直接写出BE的长度.图1 图2 图3【答案】(1)AF=BF,90°;(2)(3)见解析.【解析】解:(1)设AB交DE于O.∵∠ACB=90°,AC=BC,∴∠ABC=45°,∵DF∥AC,∴∠FDB=∠C=90°,∴∠DFB=∠DBF=45°,∴DF=DB,∵∠ADE=∠FDB=90°,∴∠ADF=∠EDB,∵DA=DE,∴△ADF≌△EDB,∴AF=BE,∴∠DAF=∠E,∵∠AOD=∠EOB,∴∠ABE=∠ADO=90°,所以答案为AF=BF,90°.(2)结论:AF=BE,∠ABE=α.理由如下:∵DF‖AC∴∠ACB=∠FDB=α,∠CAB=∠DFB,∵AC=BC,∴∠ABC=∠CAB,∴∠ABC=∠DFB,∴DB=DF,∵∠ADF=∠ADE﹣∠FDE,∠EDB=∠FDB﹣∠FDE,即∠ADF=∠EDB,∵AD=DE,∴△ADF≌△EDB,∴AF=BE,∠AFD=∠EBD∵∠AFD=∠ABC+∠FDB,∠DBE=∠ABD+∠ABE,∴∠ABE=∠FDB=α.(3)分两种情况讨论:①当点D在线段BC上时,由(2)可知:BE=AF,∵DF∥AC,∴14 AF CDBA BC==,∵AB=8,∴AF=2,∴BE=AF=2,②当点D在BC的延长线上时,∵AC∥DF,∴12 AF CDBA BC==,∵AB=8,∴AF=4,即BE=4,综上所述,BE的长度为2或4.6.(2019·开封二模)问题发现如图1,△ABC是等边三角形,点D是边AD上的一点,过点D作DE∥AC交AC于E,则线段BD与CE有何数量关系?拓展探究如图2,将△ADE绕点A逆时针旋转角α(0°<α<360°),上面的结论是否仍然成立?如果成立,请就图中给出的情况加以证明.问题解决如果△ABC的边长等于23,AD=2,直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长.图1 图2 备用图【答案】见解析.【解析】解:(1)如图1,BD=CE,理由是:∵△ABC是等边三角形,∴AB=AC,∵DE∥BC,∴△ADE是等边三角形,即AD=AE,∴BD=CE;(2)结论仍然成立,由图1得:AD=AE,由旋转性质得:∠BAD=∠CAE,∵AB=AC,∴△BAD≌△CAE,∴BD=CE;(3)分两种情况讨论,①如图所示,过D作DG⊥AB,垂足为G,∵AF⊥DE,AD=AE,∴∠DAF=∠EAF=30°,∴∠BAD=30°,由AD=2,得:DG=1,AG3由AB=3BG3由勾股定理得:BD=2.②如图,由(2)中证明可知:△BAD≌△CAE,∴BD=CE,∵AD=AE,DE⊥AC,∠ADE=60°∴∠EAF=∠FAD=30°,∴EF=FD=12AD=1,∴AF=3,∴CF=AC+CF=33,在Rt△EFC中,由勾股定理得:EC=27,∴BD=EC=27,综上所述,BD的长为2或27.7.(2019·安阳二模)(1)问题发现:如图1,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,则AB,AD,DC之间的数量关系为.(2)问题探究:如图2,在四边形ABCD中,AB∥DC,E是BC的中点,点F是DC的延长线上一点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的数量关系,并证明你的结论(3)问题解决:如图3,AB∥CD,点E在线段BC上,且BE:EC=3:4.点F在线段AE上,且∠EFD =∠EAB,直接写出AB,DF,CD之间的数量关系.图1 图2 图3【答案】(1)AD=AB+CD;(2)(3)见解析.【解析】解:(1)结论:AD=AB+CD.理由:∵AB∥CF,∴∠CFE=∠EAB,∵CE=EB,∠CEF=∠AEB,∴△CEF≌△BEA,∴AB=CF.∵AF平分∠DAB,∴∠DAF=∠EAB,∵∠EAB=∠CFE,∴∠DAF=∠DFA,∴AD=DF,∵DF=DC+CF=CD+AB,∴AD=AB+CD.(2)结论:AB=AF+CF.理由:延长AE、DC交于G,∵AB∥DG,∴∠G=∠EAB,∵CE=EB,∠CEG=∠BEA,∴△CEG≌△BEA,∴AB=CG,∠G=∠EAB,∵AE平分∠FAB,∴∠FAG=∠EAB,∵∠G=∠EAB,∴∠FAG=∠G,∴FA=FG,∵CG=CF+FG=CF+AF,∴AB=AF+CF.(3)结论:AB=34(CD+DF).延长AE、CD交于G.∵CG∥AB,∴34BE ABCE CG==,∠G=∠A,∴AB=34 CG,∵∠DFE=∠A,∴∠DFG=∠G,∴DF=DG,∴CD+DF=CD+DG=CG,∴AB=34(CD+DF).8.(2019·中原名校大联考)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点,(1)【观察猜想】图1中,线段AP与BE的数量关系是,位置关系是.(2)【探究证明】把△ADE绕点A逆时针旋转到图2的位置,(1)中的猜想是否仍然成立?若成立请证明,否请说明理由;(3)【拓展延伸】把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出线段AP长度的最大值和最小值.图1 图2【答案】(1)AP=12BE,PA⊥BE;(2)(3)见解析.【解析】解:(1)设PA交BE于点O.∵AD=AE,AC=AB,∠DAC=∠EAB,∴△DAC≌△EAB,∴BE=CD,∠ACD=∠ABE,∵∠DAC=90°,DP=PC,∴PA=12CD=PC=PD,∴PA=12BE,∠C=∠PAE,∵∠CAP+∠BAO=90°,∴∠ABO+∠BAO=90°,∴∠AOB=90°,∴PA⊥BE,(2)结论成立.理由:延长AP至M,使PM=PA,连接MC,延长PA交BE于O.∵PA=PM,PD=PC,∠APD=∠CPM,∴△APD≌△MPC,∴AD=CM,∠ADP=∠MCP,∴AD∥CM,∴∠DAC+∠ACM=180°,∵∠BAC=∠EAD=90°,∴∠EAB=∠ACM,∵AB=AC,AE=CM,∴△EAB≌△MCA,∴BE=BM,∠CAM=∠ABE,∵PA=12AM,PA=12BE,∵∠CAM+∠BAO=90°,∴∠ABE+∠BAO=90°,∴∠AOB=90°,∴PA⊥BE.(3)∵AC=10,CM=4,∴10﹣4≤AM≤10+4,∴6≤AM≤14,∵AM=2AP,∴3≤PA≤7.∴PA的最大值为7,最小值为3.9.(2018·新乡一模)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角.(1)BD与CE的数量关系是:;(2)把图1的△ABC绕点A旋转一定的角度,得到如图2所示的图形.①求证:BD=CE;②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由.(3)若AD=10,AB=6,把图1中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围.图1 图2【答案】(1)=;(2)(3)见解析. 【解析】解:∵AD=AE,AB=BC,∴AD-AB=AE-AC,即BD=CE;(2)①∵∠DAE=∠BAC,∴∠DAE+∠BAE=∠BAC+∠BAE.即∠BAD=∠CAE.在△ABD和△ACE中,AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△ACE(SAS)∴BD=CE.②BD与CE所在直线的夹角与∠DAE的度数相等. 延长DB交CE于点F.OF BEC∵△ABD≌△ACE,∴∠ADB=∠AEC∵∠AOD=∠EOF,∴180°-∠ADB-∠AOD =180°-∠AEC-∠EOF,即∠DAE=∠DFE③当B在线段AD上时,BD最小,最小值为10-6=4;当B在线段DA延长线上时,BD最大,最大值为10+6=16,即4≤BD≤16.10.(2019·河南模拟)【问题探索】(1)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D,E分别在AC、BC边上,DC=CE,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN. 探索BE与MN的数量关系. 聪明的小华推理发现PM、PN的关系为,最后推理得到BE与MN的数量关系为.【深入探究】(2)将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;【答案】见解析.【解析】解:(1)PM=PN,PM⊥PM;BE2MN;∵AM=ME,AP=PB,∴PM∥BE,PM=12 BE,同理:PN∥AD,PN=12 AD,∵AC=BC,CD=CE,∴AD=BE,∴PM=PN,∵∠ACB=90°,∴AC⊥BC,∴∵PM∥BC,PN∥AC,∴PM⊥PN,∴△PMN的等腰直角三角形,∴MN2PM,∴MN2×12 BE,∴BE2MN.(2)结论仍然成立.连接AD、延长BE交AD于点H.∵△ABC和△CDE是等腰直角三角形,∴CD=CE,CA=CB,∠ACB=∠DCE=90°,∴∠ACD=∠ECB,∴△ECB≌△DCA,∴BE=AD,∠DAC=∠EBC,∠AHB=180°-(∠HAB+∠ABH)=180°-(45°+∠HAC+∠ABH)=∠180°-(45°+∠HBC+∠ABH)=90°,∴BH⊥AD,∵M、N、P分别为AE、BD、AB的中点,∴PM∥BE,PM=12BE,PN∥AD,PN=12AD,∴PM=PN,∠MPN=90°,∴BE=2PM 2MN2.。


河南中考数学类比探究学生精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-中考数学类比探究 实战演练(一)22.(10分)如图1,在矩形ABCD 中,AB =mBC ,E 为BC 上一点,且BC =nBE ,连接AE ,过点B 作BM⊥AE ,交AE 于点M ,交AC 于点N .(1)如图2,当m =1,n =3时,求证:AN =3CN ; (2)如图3,当m =1时,求AN 与CN 之间的数量关系;图1NM E DCBACBADE M N 图2图3N M E DCBA.中考数学类比探究 实战演练(二)22. (10分)小华遇到这样一个问题:在菱形ABCD 中,∠ABC =60°,边长为4,在菱形ABCD 内部有一点P ,连接PA ,PB ,PC ,求PA +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是:如图1,将△APC 绕点C 顺时针旋转60°,恰好旋转至△DEC ,连接PE ,BD ,则BD 的长即为所求.(1)请你写出在图1中,PA +PB +PC 的最小值为________. (2)参考小华思考问题的方法,解决下列问题:①如图2,在△ABC 中,∠ACB =30°,BC =6,AC =5,在△ABC 内部有一点P ,连接PA ,PB ,PC ,求PA +PB +PC 的最小值.②如图3,在正方形ABCD 中,AB =5,P 为对角线BD 上任意一点,连接PA ,PC ,请直接写出PA +PB +PC 的最小值(保留作图痕迹).图1PADBEC BCPA图2P图3DCBA图1F E DCBA 中考数学类比探究 实战演练(三)22. (10分)如图,在Rt △ABC 中,∠ACB =90°,BC =nAC ,CD ⊥AB 于D ,点E 是直线AC 上一动点,连接DE , 过点D 作FD ⊥ED ,交直线BC 于点F ,连接EF .(1)探究发现:如图1,若n =1,点E 在线段AC 上,则tan ∠EFD =____.(2)数学思考:①如图2,若点E 在线段AC 上,则tan ∠EFD =____(用含n 的代数式表示). ②当点E 在直线AC 上运动时,①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.从“点E 是线段AC 延长线上的任意一点”或“点E 是线段AC 反向延长线上的任意一点”中,任选一种情况,在图3中画出图形,给予相应的证明或理由.(3)拓展应用:若AC,BC=DF=,请直接写出CE 的长.图2F E DCBA图3DCBA中考数学类比探究 实战演练(四)22. (10分)已知:在△AOB 与△COD 中,OA =OB ,OC =OD ,∠AOB =∠COD =90°.(1)如图1,点C ,D 分别在边OA ,OB 上,连接AD ,BC ,点M 为线段BC 的中点,连接OM ,则线段AD 与OM 之间的数量关系是__________,位置关系是_________.(2)如图2,将图1中的△COD 绕点O 逆时针旋转,旋转角为α(0°<α<90°).连接AD ,BC ,点M 为线段BC 的中点,连接OM .请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由.(3)如图3,将图1中的△COD 绕点O 逆时针旋转到使△COD 的一边OD 恰好与△AOB 的一边OA 在同一条直线上时,点C 落在OB 上,点M 为线段BC 的中点,请你判断(1)中线段AD 与OM 之间的数量关系是否发生变化,写出你的猜想,并加以证明.O图1M D C BAO图2MDCBA图3中考数学类比探究实战演练(五)22.(10分)如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.(1)求证:EF=EG.(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,求EFEG的值.E(A)B CDFGGFDCBAE图1图1GFDCBAEEACDFG(B)图1图2图3图2EACDFG(B)图2图3图3中考数学类比探究 实战演练(六)22. (10分)如图1,在等腰Rt △ABC 和等腰Rt △CDE (CD >BC )中,点C ,B ,D 在同一直线上,点M 是AE 的中点,连接MD ,MB .(1)探究线段MD ,MB 的位置关系及数量关系,并证明.(2)将图1中的△CDE 绕点C 顺时针旋转45°,使△CDE 的斜边CE 恰好与△ABC 的边BC 垂直,如图2,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若将图2中的△ABC 绕点C 逆时针旋转大于0°且小于45°的角,如图3,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.EMDCBA图1M DCBA图2ABCDM图3中考数学类比探究 实战演练(七)22. (10分)已知:在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边作正方形ADEF ,连接CF .(1)如图1,当点D 在线段BC 上时,求证:①BD ⊥CF ;②CF =BC -CD .(2)如图2,当点D 在线段BC 的延长线上时,其他条件不变,请直接写出CF ,BC ,CD 三条线段之间的关系.(3)如图3,当点D 在线段BC 的反向延长线上时,且点A ,F 分别在直线BC 的两侧,其他条件不变.①请直接写出CF ,BC ,CD 三条线段之间的关系;②若连接正方形的对角线AE ,DF ,交点为O ,连接OC ,探究△AOC 的形状,并说明理由.EDBACF图1EDA C F图2OEDB ACF图3中考数学类比探究 实战演练(八)22. (10分)在△ABC 中,∠A =90°,点D 在线段BC 上,∠EDB =12∠C ,BE ⊥DE ,垂足为E ,DE 与AB 相交于点F .(1)如图1,若点D 与点C 重合,AB =AC ,探究线段BE 与FD 的数量关系.(2)如图2,若点D 与点C 不重合,AB =AC ,探究线段BE 与FD 的数量关系,并加以证明;(3)如图3,若点D 与点C 不重合,AB =kAC ,求BEFD的值(用含k 的式子表示). C B (D )AFE图1CB DAFE图2CBD AFE图3中考数学类比探究 实战演练(九)22. (10分)点A ,B 分别是两条平行线m ,n 上任意一点,在直线n 上找一点C ,使BC =kAB ,连接AC ,在直线AC 上任取一点E ,作∠BEF =∠ABC ,EF 交直线m 于点F . (1)如图1,当∠ABC =90°,k =1时,判断线段EF 和EB 之间的数量关系,并证明.(2)如图2,当∠ABC =90°,k ≠1时,(1)中的结论还成立吗?若成立,请证明;若不成立,请重新判断线段EF 和EB 之间的数量关系.(3)如图3,当0°<∠ABC <90°,k =1时,探究EF 和EB 之间的数量关系,并证明.A FCB EA F ECBBCEFAnm图1 图2 图3中考数学类比探究实战演练(十)22.(10分)在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明CE=CF;(2)如图2,若∠ABC=90°,G是EF的中点,连接DB,DG,直接写出∠BDG的度数;(3)如图3,若∠ABC =120°,FG ∥CE ,且FG =CE ,连接DB ,DG ,求∠BDG 的度数.A BC EF D图1A BC EF DG图2A BC E FDG图3中考数学类比探究 实战演练(十一)图2BC QP E FAAF E (P )Q CB图122. (10分)已知点P 是Rt △ABC 斜边AB 上一动点(不与点A ,B 重合),分别过点A ,B 向直线CP 作垂线,垂足分别为E ,F ,Q 是斜边AB 的中点.(1)如图1,当点P 与点Q 重合时,AE 与BF 的位置关系是___________,QE 与QF 的数量关系是______________.(2)如图2,当点P 不与点Q 重合时,试判断QE 与QF 的数量关系,并给予证明.(3)如图3,当点P 在线段BA (或AB )的延长线上时,(2)中的结论是否仍然成立?请画出图形并给予证明.中考数学类比探究 实战演练(十二)22. (10分)问题解决:如图1,将正方形纸片ABCD 折叠,使点B 落在CD 边上的点E 处(不与点C ,D 重合),压平后得到折痕MN .当12CE CD =时,求AMBN的值. 类比归纳:在图1中,若13CE CD =,则AM BN 的值为__________;若14CE CD =,则AMBN 的值为__________;若1CE CD n =(n 为整数),则AMBN的值为__________.(用含n 的式子表示)联系拓广:如图2,将矩形纸片ABCD 折叠,使点B 落在CD 边上的点E 处(不与点C D ,重合),压平后得到折痕MN ,设1AB BC m =(1m >),1CE CD n =,则AMBN的值为_______.(用含m n ,的式子表示)图2图1CBD A FEM N CBDA FEM N。



类比探究专题1. 如图1,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D ,E 分别在边AB ,AC上,AD =AE ,连接DC ,BE ,点P 为DC 的中点. (1)观察猜想图1中,线段AP 与BE 的数量关系是________,位置关系是________; (2)探究证明把△ADE 绕点A 逆时针方向旋转到图2的位置,小航猜想(1)中的结论仍然成立,请你证明小航的猜想; (3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出线段AP 的取值范围.(1)操作:如图1,点O 为线段MN 的中点,直线PQ 与MN 相交于点O ,请利用图1画出一对以点O 为对称中心的全等三角形.(不写画法)根据上述操作得到的经验完成下列探究活动:(2)探究一:如图2,在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE =∠EAF ,AF 与DC 的延长线相交于点F .试探究线段AB 与AF ,CF 之间的等量关系,并证明你的结论. (3)探究二:如图3,DE ,BC 相交于点E ,BA 交DE 于点A ,且BE :EC =1:2,∠BAE =∠EDF ,CF ∥AB .若AB =5,CF =1,求DF 的长度.PEDA BC 图1PEDABC图2图1M NQ PO图2F EDC B AAB C D E F图32.特殊:(1)如图1,在等腰直角三角形ABC中,∠ACB=90°.作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD,BE.填空:①线段BD,BE的数量关系为_________________;②线段BC,DE的位置关系为_________________.一般:(2)如图2,在等腰三角形ABC中,∠ACB=α,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE,BD,BE.请判断(1)中的结论是否成立,请说明理由.特殊:(3)如图3,在等边三角形ABC中,作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD,AE.若AB=4,当△ADM 与△AFD全等时,请直接写出DE的值.M F ED CB A图1EMDCBA图2MFEDC BA图33. 已知△ABC 中,CA =CB ,0°<∠ACB ≤90°.点M ,N 分别在边CA ,CB 上(不与端点重合),BN =AM ,射线AG ∥BC 交BM 延长线于点D ,点E 在直线AN 上,EA =ED .(1)【观察猜想】如图1,点E 在射线NA 上,当∠ACB =45°时, ①线段BM 与AN 的数量关系是_________; ②∠BDE 的度数是____________.(2)【探究证明】如图2,点E 在射线AN 上,当∠ACB =30°时,判断并证明线段BM 与AN 的数量关系,求∠BDE 的度数;(3)【拓展延伸】如图3,点E 在直线AN 上,当∠ACB =60°时,AB =3,点N 是BC 边上的三等分点,直线ED 与直线BC 交于点F ,请直接写出线段CF 的长.图1A B CD ENMG图2AB CD MN EG 图3A BCG4.如图,在Rt△ABC中,∠ACB=90°,BC mAC n=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则DEDF=__________.(2)数学思考:①如图2,若点E在线段AC上,则DEDF=__________(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明.(3)拓展应用:若ACBC=DF=CE的长.FEDC BA图1图2ABCDEFDB FECA图3DC BA备用图5. (1)【问题发现】如图1,△ABC 和△CEF 都是等腰直角三角形,∠BAC =∠EFC =90°,点E 与点A 重合,则线段BE 与AF 的数量关系为__________; (2)【拓展研究】在(1)的条件下,将△CEF 绕点C 旋转,连接BE ,AF ,线段BE 与AF 的数量关系有无变化?仅就图2的情形给出证明; (3)【问题发现】当AB =AC =2,△CEF 旋转到B ,E ,F 三点共线时,直接写出线段AF 的长.(1)问题发现:如图1,在△ABC 中,∠BAC =90°,AB =AC ,点D 是BC 的中点,以点D 为顶点作正方形DFGE ,使点A ,C 分别在DE 和DF 上,连接BE ,AF ,则线段BE 和AF 数量关系是________.(2)类比探究:如图2,保持△ABC 固定不动,将正方形DFGE 绕点D 旋转α(0<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC =DF =2,在(2)的旋转过程中,连接AE ,请直接写出AE 的最大值.F图1CBA (E )EABC图2F备用图CBA图1A BC DEF G图2GFED CB A 备用图A BC DEFG6.在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是__________,CE与AD的位置关系是__________.(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明).(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=BE= ADPE的面积.(直接写出结果)P EDCBA图1图2ABCDEPPEDCBA图3图4ABCDEP7. (1)操作发现如图1,AD 是等边三角形ABC 的角平分线,请你按下列要求画图:过点A 作AM ⊥AB ,过点C 作CN ∥AB ,AM 与CN 相交于点E .则AD 与AE 的数量关系是________,∠EAC =________°. (2)问题探究将图1中的△AEC 绕点A 逆时针旋转,点C 落在点F 的位置,连接EC ,DF ,如图2所示,请你探究DF 与EC 的数量关系并说明理由. (3)拓展延伸若(2)中等边△ABC 的边长为2,当F A ⊥AC 时,请直接写出DF 2的值.在Rt △ABC 中,∠BAC =90°,AC =AB =4,D ,E 分别是边AB ,AC 的中点,若等腰Rt △ADE 绕点A 逆时针旋转,得到等腰Rt △AD 1E 1,设旋转角为α(0<α≤180°),记直线BD 1与CE 1的交点为P .(1)问题发现如图1,当α=90°时,线段BD 1的长等于__________,线段CE 1的长等于__________. (2)探究证明如图2,当α=135°时,求证:BD 1=CE 1,且BD 1⊥CE 1. (3)问题解决求点P 到AB 所在直线的距离的最大值.(直接写出结果)图1AB CD图2EFDCBA备用图CBAE1(D1)ABCDE PEDCBAD1E1图2图18. 如图1,在正方形ABCD 和正方形AB′C′D′中,AB =2,AB′=,连接CC′.(1)问题发现:CC BB'='__________;(2)拓展探究:将正方形AB′C′D′绕点A 逆时针旋转,记旋转角为θ,连接BB′,试判断:当0°≤θ<360°时,CC BB ''的值有无变化?请仅就图2中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C ,C′,D′三点共线时BB′的长.问题发现:如图1,△ABC 是等边三角形,点D 是边AB 上的一点,过点D 作DE ∥BC 交AC 于E ,则线段BD 与CE 的数量关系为___________;拓展探究:如图2,将△ADE 绕点A 逆时针旋转角α(0°<α<360°),上面的结论是否仍然成立?如果成立,请就图中给出的情况加以证明;问题解决:如果△ABC的边长等于AD =2,直接写出当△ADE 旋转到DE 与AC 所在的直线垂直时BD 的长.D′C′B′ABCD 图1图2DCBA B′C′D′A BCD备用图图1EDCBA 图2ABCDE备用图E D A9. 如图1,已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,垂足为点E ,GF ⊥CD ,垂足为点F . (1)证明与推断:①求证:四边形CEGF 是正方形;②推断AGBE的值为_______.(2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG 与BE 之间的数量关系,并说明理由. (3)拓展与运用:正方形CEGF 在旋转过程中,当B ,E ,F 三点在一条直线上时,如图3所示,延长CG 交AD 于点H .若AG =6,GH=BC =________.GFDC BAE图1ABCD EFG图2H GF EDCBA 图310. (1)阅读理解利用旋转变换解决数学问题是一种常用的方法.如图1,点P 是等边三角形ABC 内一点,P A =1,PB,PC =2.求∠BPC 的度数. 为利用已知条件,不妨把△BPC 绕点C 顺时针旋转60°得△AP′C ,连接PP′,则PP′的长为__________;在△P AP′中,易证∠P AP′=90°,且∠PP′A 的度数为__________,综上可得∠BPC 的度数为__________. (2)类比迁移 如图2,点P 是等腰Rt △ABC 内一点,∠ACB =90°,P A =2,PB,PC =1.求∠APC 的度数. (3)拓展应用如图3,在四边形ABCD 中,BC =3,CD =5,AB =AC =12AD ,∠BAC =2∠ADC ,请直接写出BD 的长.P′ABCP图1图2P CBAD图3C BA11. 如图,在□ABCD 中,AC 与BD 交于点O ,以点O 为顶点的∠EOF 的两边分别与边AB ,AD 交于点E ,F ,且∠EOF 与∠BAD 互补. (1)观察猜想若四边形ABCD 是正方形,则线段OE 与OF 有何数量关系?请直接写出结论.(2)延伸探究若四边形ABCD 是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由. (3)拓展证明若AB :AD =m :n ,探索线段OE 与OF 的数量关系,并证明你的结论.(1)阅读理解:如图1,在四边形ABCD 中,AB ∥DC ,E 是BC 的中点,若AE 是∠BAD 的平分线,试判断AB ,AD ,DC 之间的等量关系.解决此问题可以用如下方法:延长AE 交DC 的延长线于点F ,易证△AEB ≌△FEC ,得到AB =FC ,从而把AB ,AD ,DC 转化在一个三角形中即可判断.AB ,AD ,DC 之间的等量关系为_____________;(2)问题探究:如图2,在四边形ABCD 中,AB ∥DC ,AF 与DC 的延长线交于点F ,E 是BC 的中点,若AE 是∠BAF 的平分线,试探究AB ,AF ,CF 之间的等量关系,并证明你的结论.(3)问题解决:如图3,AB ∥CF ,AE 与BC 交于点E ,BE :EC =2:3,点D 在线段AE 上,且∠EDF =∠BAE ,试判断AB ,DF ,CF 之间的数量关系,并证明你的结论.A BCDOEFABCD EF图1ABCDE F图2A BCDE F图312. 如图1,菱形ABCD 与菱形GECF 的顶点C 重合,点G 在对角线AC 上,且∠BCD =∠ECF =60°. (1)问题发现: AGBE的值为__________. (2)探究与证明:将菱形GECF 绕点C 按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG 与BE 之间的数量关系,并说明理由. (3)拓展与运用:菱形GECF 在旋转过程中,当点A ,G ,F 三点在一条直线上时,如图3所示,连接CG 并延长,交AD 于点H ,若CE =2,GHAH 的长为__________.已知∠AOB =90°,点C 是∠AOB 的角平分线OP 上的任意一点,现有一个直角∠MCN 绕点C 旋转,两直角边CM ,CN 分别与直线OA ,OB 相交于点D ,点E .(1)如图1,若CD ⊥OA ,猜想线段OD ,OE ,OC 之间的数量关系,并说明理由.(2)如图2,若点D 在射线OA 上,且CD 与OA 不垂直,则(1)中的数量关系是否仍成立?如成立,请说明理由;如不成立,请写出线段OD ,OE ,OC 之间的数量关系,并加以证明.图1AB CDEFGG FE DCB A图2H图3AB CD E FG(3)如图3,若点D 在射线OA 的反向延长线上,且OD =2,OE =8,请直接写出线段CE 的长度.图1OABC D EMPN N PMED CBAO图2图3O ABCD E MPN13.如图,在矩形ABCD中,AB=8,AD=6,点E,F分别是边DC,DA的中点,四边形DFGE为矩形,连接BG.(1)问题发现在图1中,CEBG__________.(2)拓展探究将图1中的矩形DFGE绕点D旋转一周,在旋转过程中,CEBG的大小有无变化?请仅就图2的情形给出证明. (3)问题解决当矩形DFGE 旋转至B ,G ,E 三点共线时,请直接写出线段CE 的长.GFED CBA 图1图2ABCDEFG备用图ABCD14. 四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD 等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD 中,AB =AD ,CB =CD ,则AC 与BD 的位置关系是__________,请说明理由.(2)试探究图1中四边形ABCD 的两组对边AB ,CD 与BC ,AD 之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt △ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连接CE ,BG ,GE ,已知AC =4,AB =5,求GE 的长.观察猜想(1)如图1,在Rt △ABC 中,∠BAC =90°,AB =AC =3,点D 与点A 重合,点E 在边BC 上,连接DE ,将线段DE 绕点D 顺时针旋转90°得到线段DF ,连接BF ,BE 与BF 的位置关系是_________,BE +BF =_________; 探究证明(2)在(1)中,如果将点D 沿AB 方向移动,使AD =1,其余条件不变,如图2,判断BE 与BF 的位置关系,并求BE +BF 的值,请写出你的理由或计算过程; 拓展延伸ABCD图1图2DCB AABCDEFG图3(3)如图3,在△ABC 中,AB =AC ,∠BAC =α,点D 在边BA 的延长线上,BD =n ,连接DE ,将线段DE 绕着点D 顺时针旋转,旋转角∠EDF =α,连接BF ,则BE +BF 的值是多少?请用含有n ,α的式子直接写出结论.图1A (D )B CE FD FE C B A 图2图3A C D E F。
欢迎共阅第六讲几何类比探究(一)几何类比探究是河南中考数学的重点、难点,虽是考试难点,但依然有法可破!【知识点睛?】1.?类比探究一般会围绕一个不变结构进行考查.常见结构有:平行结构、直角结构、旋转结构、中点结构.?PA=①线段PB= ,PC= ;②猜想:PA2,PB2,PQ2三者之间的数量关系为;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)例3.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC.以点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合).如图1,DE与AC交于点P,易证:BD=DP.(1)在图2中,DE与CA的延长线交于点P,则BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由.(2)在图3中,DE与AC的延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.2.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB的中点,点P为直线BC上的动点(不与点B、点C重合),连接OC,OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系:________________;(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.图1 图2 图33如图,△ABC中,点E,P在边AB上,且AE=BP,过点E,P作BC的平行线,4、在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长交AB于点F.(1)如图1,当∠BAC=90°,∠B=30°,DE=EA时,求FBFA的值;(2)如图2,当△ABC为锐角三角形,DE=EA时,求FBFA的值;(3)如图3,当△ABC为锐角三角形,DE=nEA时,求FBFA的值.第六讲几何类比探究(二)例1.如图1,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD 交于点E和点F(点F与点C,D不重合).(1)如图1,当α=90°时,DE,DF,AD之间满足的数量关系是____________;(2)如图2,将图1中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,特殊发现:如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).问题探究:把图1中的△AEF绕着点A顺时针旋转.(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由.(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)记ACkBC,当k为何值时,△CPE总是等边三角形(请直接写出k的值,不必说明理由)?例4.(2017洛阳一模)(10分)如图①,C为线段BE上的一点,分别以BC 和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN(1)线段MN和GD的数量关系是,位置关系是;(1)发现:在图1中,=;(2)应用:如图2,将△ADE绕点A旋转,请求出的值;(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出的值.例7.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.(1)如图1,求证:AE=BD;(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.。