半导体物理6
- 格式:ppt
- 大小:14.35 MB
- 文档页数:76

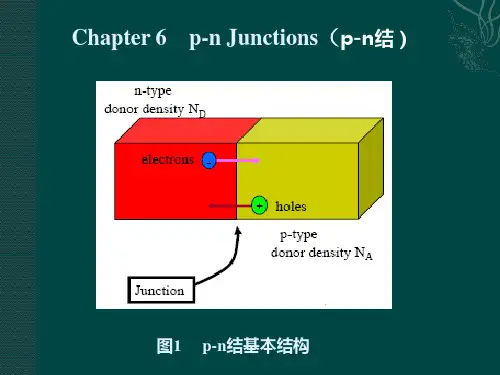







第6章 p-n 结1、一个Ge 突变结的p 区n 区掺杂浓度分别为N A =1017cm -3和N D =5´1015cm -3,求该pn 结室温下的自建电势。
解:pn 结的自建电势结的自建电势 2(ln)D A D iN N kT V qn=已知室温下,0.026kT =eV ,Ge 的本征载流子密度1332.410 cm i n -=´代入后算得:1517132510100.026ln0.36(2.410)D V V ´´=´=´4.4.证明反向饱和电流公式(证明反向饱和电流公式(证明反向饱和电流公式(6-356-356-35)可改写为)可改写为)可改写为2211()(1)i s n n p p b k T J b q L L s s s =++ 式中npb m m =,n s 和p s 分别为n 型和p 型半导体电导率,i s 为本征半导体电导率。
证明:将爱因斯坦关系式p p kT D qm =和nnkT D q m =代入式(式(6-356-356-35))得 0000()p n p n S p n n pn p n p p nn p J kT n kT p kT L L L L m m m m m m =+=+因为002i p p n n p=,002i n nn p n =,上式可进一步改写为,上式可进一步改写为00221111()()S n p i n p i n p p p n n n p p nJ kT n qkT n L p L n L L m m m m m m s s =+=+ 又因为又因为()i i n p n q s m m =+22222222()(1)i i n p i p n q n q b s m m m =+=+即22222222()(1)i i i n p p n q q b s s m m m ==++ 将此结果代入原式即得证将此结果代入原式即得证2222221111()()(1)(1)n p i i Sp np pn np pnqkT b kT J q b LL q b L L m m s s mssss=+=××+++ 注:严格说,迁移率与杂质浓度有关,因而同种载流子的迁移率在掺杂浓度不同的p 区和n区中并不完全相同,因而所证关系只能说是一种近似。


第三部分 载流子输运现象一、半导体导电性 1、电导率(电阻率)实际问题中,通过半导体的电流往往是不均匀的。
不能只讲通过半导体的总电流强度而必须具体地分析电流的不均匀分布。
图1 用探针测电流 图2 集成片的电流分布( 图1电流形成一个以探针针尖为中心、沿半径四外散开的电流分布图2从表面向内,每一层杂质浓度都不一样,通过它的电流在各层之间是不均匀的,越近表面电流越强。
)为了描述导电体内各点电流强弱的不均匀性,通常采用欧姆定律的微分形式:可从欧姆定律RVI =导出,取一个长为L ,横截面为S 的均匀导电体,当两端加电压V 时,在这样一个形状规则的均匀材料中,电流是均匀的,电流密度j 在各处是一样的。
总电流强度Sj I =同时,电场强度也是均匀的,有LE V = 则,RLESj = 得,E j ρ1=其中LRS=ρ,即材料的电阻率。
单位: 定义,ρσ1=,称为电导率。
单位:所以,欧姆定律的微分形式E j σ= 。
单位:安培/厘米2 (A/cm 2);注意:在这里,微分形式的欧姆定律虽然是从均匀导电情况导出的,显然,它也适用于非均匀的情况。
因为对于非均匀导体,我们可以取一个小体积元,当小体积元足够小时,可以看成是均匀的。
从微分欧姆定律看出,材料的导电能力是用电导率来表示。
通过前面学习已知,一般掺杂半导体在常温范围内导电性能主要由掺杂决定。
那末,电导率和掺杂是什么关系呢?要解决这个问题,就有必要分析—下,在电场作用下载流子如何形成电流的机理。
下面我们结合N 型半导体分析这个问题。
我们应当知道,即使没有电场作用,电子也并不是静止不动的,而是象气体中分子那样,杂乱无章地进行热运动。
由于电子质量比分子小得多,所以,电子热运动的速度比气体分子要大得多。
具体说,按照热运动理论,微观粒子无规则热运动的平均动能与绝对温度T 有如下关系:平均热运动动能2*2123t n k v m kT E ==如果用V t 表示半导体中电子的平均热运动速度,T=300K, 并且代入电子质量m 。