半导体物理第六章1
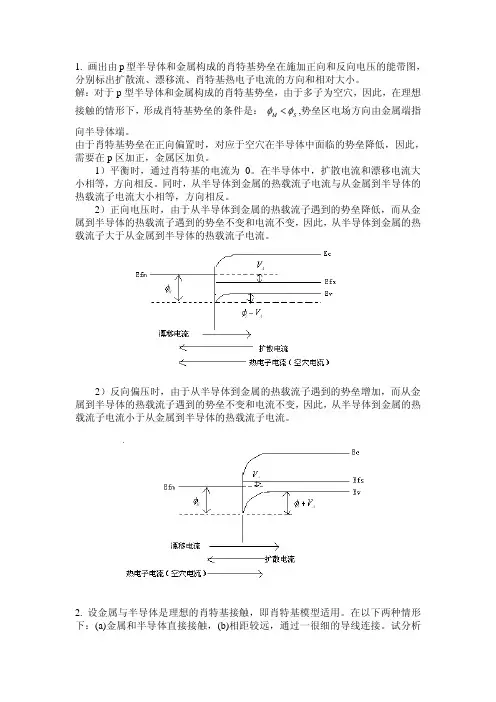
- 格式:pdf
- 大小:396.92 KB
- 文档页数:10








第6章 p-n 结1、一个Ge 突变结的p 区n 区掺杂浓度分别为N A =1017cm -3和N D =5´1015cm -3,求该pn 结室温下的自建电势。
解:pn 结的自建电势结的自建电势 2(ln)D A D iN N kT V qn=已知室温下,0.026kT =eV ,Ge 的本征载流子密度1332.410 cm i n -=´代入后算得:1517132510100.026ln0.36(2.410)D V V ´´=´=´4.4.证明反向饱和电流公式(证明反向饱和电流公式(证明反向饱和电流公式(6-356-356-35)可改写为)可改写为)可改写为2211()(1)i s n n p p b k T J b q L L s s s =++ 式中npb m m =,n s 和p s 分别为n 型和p 型半导体电导率,i s 为本征半导体电导率。
证明:将爱因斯坦关系式p p kT D qm =和nnkT D q m =代入式(式(6-356-356-35))得 0000()p n p n S p n n pn p n p p nn p J kT n kT p kT L L L L m m m m m m =+=+因为002i p p n n p=,002i n nn p n =,上式可进一步改写为,上式可进一步改写为00221111()()S n p i n p i n p p p n n n p p nJ kT n qkT n L p L n L L m m m m m m s s =+=+ 又因为又因为()i i n p n q s m m =+22222222()(1)i i n p i p n q n q b s m m m =+=+即22222222()(1)i i i n p p n q q b s s m m m ==++ 将此结果代入原式即得证将此结果代入原式即得证2222221111()()(1)(1)n p i i Sp np pn np pnqkT b kT J q b LL q b L L m m s s mssss=+=××+++ 注:严格说,迁移率与杂质浓度有关,因而同种载流子的迁移率在掺杂浓度不同的p 区和n区中并不完全相同,因而所证关系只能说是一种近似。

第六章 非平衡载流子处于热平衡状态的半导体在一定温度下载流子密度是一定的。
但在外界作用下,热平衡状态将被破坏,能带中的载流子数将发生明显改变,产生非平衡载流子。
在半导体中非平衡载流子具有极其重要的作用,许多效应都是由它们引起的,如晶体管电流放大,半导体发光和光电导等都与非平衡载流子密切相关。
在大多数情况下,非平衡载流子都是在半导体的局部区域产生的,这些载流子除了在电场作用下作漂移运动外,还要作扩散运动。
本章主要讨论非平衡载流子的运动规律及其产生和复合机理。
§6-1 非平衡载流子的产生和复合一.非平衡载流子的产生。
若用n 0和p 0分别表示热平衡时的电子和空穴密度,则当对半导体施加外界作用使之处于非平衡状态时,半导体中的载流子密度就不再是n 0和p 0了,要比它们多出一部分。
比平衡态多出的这部分载流子称过剩载流子,习惯上也称非平衡载流子。
设想有一块n 型半导体,若用光子能量大于其禁带宽度的光照射该半导体,则可将其价带中的电子激发到导带,使导带比热平衡时多出了一部分电子n ∆,价带多出了一部分空穴p ∆,从而有:0n n n -=∆ (6-1) 0p p p -=∆ (6-2) 且 n ∆=p ∆ (6-3) 式中,n 和p 分别为非平衡状态下的电子和空穴密度,n ∆称非平衡多子,p ∆称非平衡少子,对于p 型半导体则相反。
n ∆和p ∆统称非平衡载流子。
图6-1为光照产生非平衡载流子的示意图。
通过光照产生非平衡载流子的方法称光注入,如果非平衡载流子密度远小于热平衡多子密度则称小注入。
虽然小注入对多子密度的影响可以忽略,但是对少子密度的影响却可以很大。
光注入产生的非平衡载流子可以使半导体的电导率由热平衡时的0σ增加到σσσ∆+=0,其中,σ∆称附加电导率或光电导,并有:p n pe ne μμσ∆+∆=∆ (6-4) 若n ∆=p ∆,则 )(p n pe μμσ+∆=∆ (6-5) 通过附加电导率的测量可直接检验非平衡载流子是否存在。

山东大学《半导体物理》期末复习知识点第六章 pn结6.1 理论概要与重点分析(1)pn结是将同种半导体材料的n型和p型两部分紧密结合在一起,在交界处形成一个结,即称为pn结。
为使性能优越,一般采用合金法、扩散法、外延生长法和离子注入法等,改变其掺杂性质来实现这种“紧密接触”的。
pn结是重要半导体器件,如结型晶体管及其相应的集成电路的工作核心。
设两种杂质的交界面为xj,如果杂质有一个较宽的补偿过度阶段,为缓变结,较深的扩散法一般属此种情况。
(2)由于在结的两边两种载流子相差悬殊而发生扩散。
n区中的电子流入p区,在结附近留下不可以移动的电离施主;同样p区中的空穴流入n区在结的附近留下不可移动的电离受主,形成一个n区为正,p区为负的电偶极层,产生由n区指向p区的自建电场,此电场的作用是阻止载流子进一步相互扩散。
或者说产生了一个与扩散相反的载流子漂移,当两者达到平衡时,载流子通过结的净流动为零,达到平衡。
建立起一个稳定的空间电荷区和一个稳定的自建电场。
n型的一边带正电,电动势高;p型一边带负电,电势低,所产生电动势差称为pn结接触电动势差。
这个电动势差对n型区的电子和p型区的空穴各自向对方,运动都形成势垒,使整个结构在结区形成能带弯曲,其弯曲的高度称为势垒高度,它恰恰补偿了原来两边半导体中费米能级的高度差,使两边达到等高的统一费米能级。
山东大学《半导体物理》期末复习知识点(3)pn结上加正向电压V(p型一端接正,n型一端接负)时,外加电压电场与内建电场的方向相反,使内建电场减弱,势垒区变窄,势垒高度由平衡时的q VD变为q(VD-V)。
两区的费米能级分开为EnF-EpF=qV这时由内建电场引起载流子的漂移减弱,扩散相对增强。
于是有一个净的扩散电流从p区通过结流入n区,这便是pn结的正向电流。
随外加电压V的增加,势垒高度越来越小,载流子漂移越来越小,扩散进一步增加。
因此随外加正向电压的增加,正向电流迅速增大。
第6章 pn结把一块p型半导体和一块n型半导体键合在一起,就形成了pn结。
pn 结是几乎一切半导体器件的结构基础,了解和掌握pn结的性质具有很重要的实际意义。
§6.1 pn结及其热平衡状态下的能带结构一、pn结的形成及其杂质分布半导体产业形成50余年来,已开发了多种形成pn结的方法,各有其特点。
1、合金法把一小粒高纯铝置于n型单晶硅片的清洁表面上,加热到略高于Al-Si 系统共熔点(580℃)的温度,形成铝硅熔融体,然后降低温度使之凝固,这时在n型硅片的表面就会形成—含有高浓度铝的p型硅薄层,它与n型硅衬底的界面即为pn结(这时称为铝硅合金结)。
欲在p型硅上用同样的方法制造pn 结,须改用金锑(Au-Sb)合金,即用真空镀膜法在p型硅的清洁表面镀覆一层含锑0.1%的金膜,然后在400℃左右合金化。
合金结的特点是合金掺杂层的杂质浓度高,而且分布均匀;由于所用衬底一般是杂质浓度较低且分布均匀的硅片,因此形成的pn结具有杂质浓度突变性较大的特点,如图6-1所示。
具有这种形式杂质分布的pn 结通常称为单边突变结(p+n结或pn+结)。
合金结的深度对合金过程的温度和时间十分敏感,较难控制。
目前已基本淘汰。
N(x)N DN Ax jxN A图6-1 合金结的杂质分布图6-2 扩散法制造pn结的过程x jN D2、扩散法1956年发明的能精确控制杂质分布的固态扩散法为半导体器件的产业化及其后的长足发展奠定了基础。
扩散法利用杂质原子在高温下能以一定速率向固体内部扩散并形成一定分布的性质在半导体内形成pn结。
由于杂质在某些物质,例如SiO2中的扩散系数极低,利用氧化和光刻在硅表面形成选择扩散的窗口,可以实现pn结的平面布局,如图6-2所示,从而诞生了以氧化、光刻、扩散为核心的半导体平面工艺,开创了以集成电路为标志的微电子时代。
用扩散法形成的杂质分布由扩散过程及杂质补偿决定。
在表面杂质浓度不变的条件下形成的是余误差分布,在杂质总量不变的条件下形成的是高斯分布,如本节后的附图所示。
3、其他方法形成pn结的方法还有离子注入法、外延法和直接键合法等,而且这些方法已逐渐成为半导体工业的主流工艺。
《半导体工艺》课程将详细介绍,这里不赘述。
4、pn结的杂质分布 pn结的杂质分布一般可近似为两种,即突变结和线性缓变结。
合金pn结、高表面浓度的浅扩散结、用离子注入、外延和直接键合法制备的结一般可认为是突变结,而低表面浓度的深扩散结一般视为线性缓变结。
直接键合法制备的突变结是最理想的突变结。
图6-3 扩散结的杂质分布形式x jxN DN A(0)x jx jN DN A(x)N A(x)N A(0)N A(0)N DxxN Dx jxN DN Ax jx j二、pn结的空间电荷区与内建电场考虑两块半导体单晶,一块是n型,一块是p型。
独处的n型和p型半导体靠电离杂质和少数载流子与其多数载流子保持电中性。
但当这两块半导体紧密结合形成pn结时,其间的载流子密度梯度导致空穴从p区向n 区、电子从n区向p区扩散。
对于p区,空穴离开后,留下了不可动的带负电荷的电离受主,这些电离受主,没有正电荷与之保持电中性。
因此,在pn结附近的p 型侧出现了一个负电荷区。
同理,在pn结附近的n 型侧出现了由电离施主构成的正电荷区。
通常把pn结附近的这些由电离施主和电离受主所带电荷称为空间电荷,所在区域称为空间电荷区。
空间电荷区中的这些电荷产生了从n区指向p区,即从正电荷指向负电荷的电场,称为内建电场。
在内建电场作用下,载流子作漂移运动。
显然,电子和空穴的漂移运动方向与它们各自的扩散运动方向相反。
因此,内建电场起着阻碍电子和空穴继续扩散的作用。
随着扩散运动的进行,空间电荷逐渐增多,空间电荷区也逐渐扩展;同时,内建电场逐渐增强,载流子的漂移运动也逐渐加强。
在无外加电压的情况下,载流子的扩散和漂移最终将达到动态平衡,两种载流子的扩散电流和漂移电流各自大小相等、方向相反而抵消。
因此没有净电流流过pn结。
这时空间电荷的数量一定,空间电荷区不再继续扩展而保持一定的宽度和一定的内建电场强度。
一般称这种情况为热平衡状态下的pn结。
三、热平衡状态下的pn结能带结构1、能带弯曲当两块半导体结合形成pn结时,按照费米能级的意义,系统应有统一的费米能级E F。
这是通过电子从费米能级高的n区流向费米能级低的p 区,以及空穴从p区流向n区,使E Fn下移,E Fp上升,直至E Fn=E Fp来实现的。
随着费米能级的移动,空间电荷区外的整个能带随之平移,从而导致空间电荷区内能带弯曲,使空间电荷区费米能级与导带底和价带顶的距离处处不同,如图6-4所示。
事实上,空间电荷区的能带弯曲是内建电场的结果。
由于内建电场从n指向p,空间电荷区内电势V(x)由n 向p降低(E=-dV/dx),电子的电势能-qV(x)则由n向p升高,即p区能带相对n区上移,直至费米能级处处相等。
由于能带弯曲,电子从势能低的n区向p区运动时面临这一势能变化形成的势垒。
同样,空穴要从p 区向n区运动时也会受到这个势垒的阻挡。
图6-4 热平衡状态下pn结的能带图2、热平衡pn结的费米能级本小节进一步证明热平衡状态下pn结中费米能级处处相等。
热平衡pn结中不存在外加电场,但存在自建电场。
就电子而言,这时流过pn结的总电子电流密度J n应等于由载流子密度差引起的电子扩散电流密度和自建电场产生的电子漂移电流密度之和,即(6-1)由(6-2)得(6-3)将式(6-3)代入式(6-1)并考虑到D n=kTμn/q,得(6-4)其中(6-5)表示自建电场引起的能带弯曲。
所以,式(6-4)实为(6-6)因为热平衡状态下J n=0,上式表明热平衡时(6-7)对空穴电流也可得到类似结果,即(6-8)3、广义欧姆定律对n=n0+n、p=p0+p的非平衡pn结,用同样的推演可得到类似结果:;(6-9)以上两式被称作广义欧姆定律。
该式表明,若费米能级随位置变化,则pn结中必有电流;当电流密度一定时,载流子密度大的地方,E F 随位置变化小,而载流子密度小的地方,E F随位置变化就较大。
四、pn结的接触电势差平衡pn结空间电荷区两端的电势差V D称为pn结的接触电势差或内建电势差。
相应的电子势能之差,即能带的弯曲量qV D,称为pn结的势垒高度从图6-4可知,势垒高度正好补偿了n 区和p区费米能级之差,使平衡pn结的费米能级处处相等,因此令n n0、n p0分别表示n区和p 区的平衡电子密度,则对非简并半导体Vx px nV(x)E(x)p p0V DE CpE VpE CnE Vn-qV Dx(a)(b)(c)Ex px nn p0n n0p n0x nx pxn0(x)p0(x)图6-5 热平衡pn结势垒区中的电势(a)、电势能(b)和载流子密度(c)两式相除取对数得因为n n0≈N D,n p0≈n i2/ N A,所以(6-10) p0 n0上式表明,V D和pn结两边的掺杂浓度、温度、以及材料的禁带宽度有关。
在一定的温度下,突变结两边掺杂浓度越高,接触电势差V D越大,禁带宽度越大,n i越小,V D也越大,所以硅pn结比锗pn结V D大。
若N A=1017cm-3,N D=1015cm-3,在室温下可以算得V D对硅为0.7 V,对锗为0.32 V,对砷化镓为1 V。
五、热平衡pn结的载流子分布对图6-5所示的热平衡pn结,取p区电势为零,则势垒区中某点x的电势V (x)为正值。
越接近n区的点,其电势越高,到势垒区邻接n区的边界x n处,电势达到最高值V D。
n 区电子的势能E(x n)= E cn=-qV D,势垒区内点x处电子的势能为E(x)=-qV (x),因而电子在p区比在n区势能高qV D,在势垒区比在n区高(qV D-qV (x))。
对非简并材料,势垒区内点x处的电子密度n0(x)可表示为(6-11)因为E cn=-qV D,E(x)=-qV (x),所以(6-12)当x=x n时,V(x)=V D,所以n(x n)= n n0;当x=x p时,V(x)=0,所以n(x p)= n n0exp[-qV D/(kT)],而n(x p)就是p区中的热平衡电子密度n p0,因此,势垒区中热平衡电子密度又可表示为(6-13 )该式表明,势垒区中电子密度随着电势升高而指数地从p区的少子水平升高到n区的多子水平。
同理,可以求出点x处的空穴密度:(6-14)式中,p n0是n区热平衡空穴密度。
当x=x n时,V(x)=V D,故得p(x n)=p n0;当x=x p时,V(x)=0,则p(x p)= p n0exp[qV D/(kT)],p(x p)就是p 区中平衡多数载流子空穴的密度p p0。
因此,热平衡状态下势垒区中的空穴密度又可表示为(6-15)它表示,势垒区中空穴密度随着电势升高而指数地从p区的多子水平降低到n区的少子水平。
以上结果反映的热平衡pn结中电子和空穴的密度分布如图6-5(c)所示。
利用公式(6-12)-(6-15)可以估算pn结势垒区中各处的载流子密度。
例如,势垒区内电势能比n区导带底高0.1eV处的电子密度为若设势垒高度为0.7eV,则该处的空穴密度为可见,势垒区中势能仅比n 区导带底高0.1eV处的价带空穴的密度只有p区多数载流子密度的10-10倍,而该处的导带电子密度也只有n区多数载流子的1/50。
一般情况下,势垒区中的杂质在室温附近虽已全部电离,但其中的载流子密度比起n区和p区的多数载流子密度来仍小得多。
这是因为内建电场引起势垒区内能带弯曲,而费米能级保持不变的结果,或说内建电场将势垒区内载流子扫除殆尽的结果。
所以通常也称势垒区为耗尽区,认为其中载流子密度极小,可以忽略。
第5章习题18改为:一块施主浓度为21016 cm-3的硅片,含均匀分布的金,浓度为31015 cm-3,表面复合中心密度为1010cm-2,已知硅中金的r p=1.15 10-7cm3/s,表面复合中心的r S=2 10-6 cm3/s,求:1)小注入条件下的少子寿命,扩散长度和表面复合速度;2)在产生率g=1017/s. cm3的均匀光照下的表面空穴密度和表面处的空穴流密度附图:扩散杂质的两种主要分布形式扩散深度x j (m)扩散深度x j (m)余误差分布高斯分布。