铁一中五模--试题

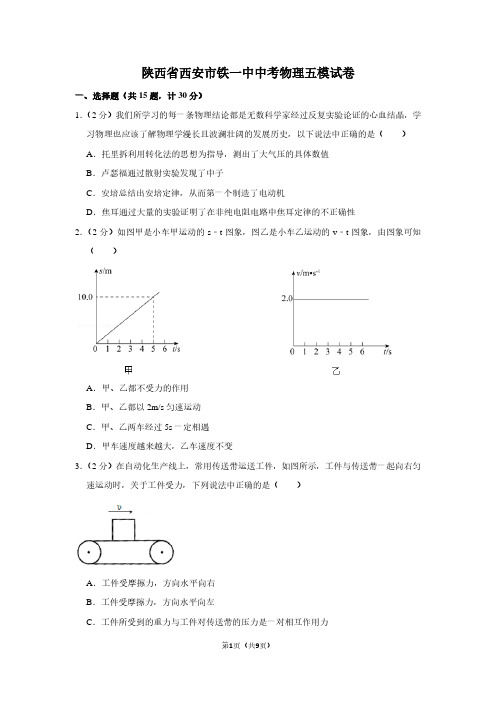
陕西省西安市铁一中中考物理五模试卷一、选择题（共15题，计30分）1．（2分）我们所学习的每一条物理结论都是无数科学家经过反复实验论证的心血结晶，学习物理也应该了解物理学漫长且波澜壮阔的发展历史，以下说法中正确的是（）A．托里拆利用转化法的思想为指导，测出了大气压的具体数值B．卢瑟福通过散射实验发现了中子C．安培总结出安培定律，从而第一个制造了电动机D．焦耳通过大量的实验证明了在非纯电阻电路中焦耳定律的不正确性2．（2分）如图甲是小车甲运动的s﹣t图象，图乙是小车乙运动的v﹣t图象，由图象可知（）A．甲、乙都不受力的作用B．甲、乙都以2m/s匀速运动C．甲、乙两车经过5s一定相遇D．甲车速度越来越大，乙车速度不变3．（2分）在自动化生产线上，常用传送带运送工件，如图所示，工件与传送带一起向右匀速运动时，关于工件受力，下列说法中正确的是（）A．工件受摩擦力，方向水平向右B．工件受摩擦力，方向水平向左C．工件所受到的重力与工件对传送带的压力是一对相互作用力D．工件对传送带的压力与传送带对工件的支持力是一对相互作用力4．（2分）如图所示是内燃机的某一个工作冲程，选项中四幅图中与其能量转化形式相同的是（）A．B．C．D．5．（2分）如图所示实验中，不能说明“流速大小对流体压强有影响”的是（）A．吹气时A管中水面上升B．用吸管从瓶中吸饮料C．吹气时纸片向下凹陷D．吹气时纸条向上飘6．（2分）烛焰通过焦距为10cm的甲凸透镜在光屏上成清晰的像，如图所示。

现用焦距为5cm的乙凸透镜替换甲，不改变蜡烛和凸透镜的位置，关于乙凸透镜的成像情况，正确的说法是（）A．要在光屏上成清晰的像，光屏应向右移动B．要在光屏上成清晰的像，光屏应向左移动C．移动光屏，可以得到一个清晰放大的实像D．移动光屏，可以得到一个清晰放大的虚像7．（2分）明明晚上做作业，把台灯插头插在书桌边的插座上，闭合台灯开关，发现台灯不亮，原本发光的右侧电灯熄灭，但左侧灯泡仍正常工作（如图所示）．将台灯插头从插座上拔下后，他用试电笔分别插入插座两孔中，结果发现试电笔的氖管都发光，则故障原因（）A．可能是进户线的火线上出现了断路B．可能是进户线的零线出现了断路C．一定是a、b两点间的导线出现了断路D．一定是d点左侧的零线出现了断路8．（2分）下列实验描述的现象不能体现有新物质生成的是（）A．澄清石灰水变浑浊B．生成黑色固体C．生成刺激性气味气体D．发现白光二、填空与作图（共7小题，计19分）9．（4分）随着社会的进步，光纤网络开始进入普通老百姓家庭，光纤的主要用途是（通信、照明），激光在光导纤维中不断的（反射、折射）．电磁波可作为信息的载体，电磁波的传播介质（不需要、需要）．其频率越大，波长。

2023年陕西省西安市铁一中学中考第五次模考化学试题学校:___________姓名：___________班级：___________考号：___________一、单选题A．B．C．D．A．A B．B C．C D．D9．已知某固体粉率是由NaCl，Ba(NO3)2，CuSO4、Na2SO4、Na2CO3中的一种或几种组成，取该固体粉末适量，加足量的水，振荡后呈浑浊，再加足量稀盐酸，沉淀不溶解，过滤后得无色滤液，取滤液并滴加AgNO3溶液产生白色沉淀，对原固体粉末的判断正确的是A．可能含CuSO4和Na2CO3B．一定含NaCl、Ba(NO3)2、Na2SO4C．可能含NaCl，一定含Ba(NO3)2、Na2SO4D．可能含NaCl、Na2SO4二、填空题10．春风和煦，西安文旅全面复苏。

(1)美食：羊肉泡馍、炸油糕、锅盔、biangbiang面……，为了使营养均衡，享用这些美食时，还应补充富含______ (填一种有机营养素)的食物。

(2)美景：西安大唐芙蓉园是以盛唐文化为内涵，主体结构采用全现浇钢筋混凝土框架仿古结构。

钢筋混凝土与玻璃钢同属于______(填“金属”或“复合”)材料。

(3)文化：有人说“西安这座城，吹过的风都是文化，踩的地全是历史”。

碑林乃书法圣地，书法使用墨汁书写长久保存的原因是______。

11．“宏观-微观-符号”三重表征是化学学习的重要方法。

(1)甲图中x的值为______。

(2)写出乙图中阴离子的符号为______；乙中B与丙中⑤属于同种元素，是因为它们具有相同的_____。

(3)丙图中只有微观意义的是_______(填序号)。

12．化学知识可以帮助我们认识并解决生活中的很多问题。

(1)鉴别厨房里的小苏打和面粉，可以选用______ (填“食醋”、“食用油”或“酱油”)。

(2)“84消毒液"的制备原理为222X H O Cl NaOH NaClO +=++，则X 的化学式为______。

2023年陕西省西安市碑林区铁一中学中考五模数学试卷学校:___________姓名：___________班级：___________考号：___________
A．B．C．D．
二、填空题
三、解答题
18．如图，矩形ABCD中，点E是AD的中点，连接EB，EC．
=；
(1)求证：EB EC
(2)若60
AE=，求AB的长．
∠=︒，1
BEC
19．为了贯彻落实健康第一的指导思想，促进学生全面发展，国家每年都要对中学生进行一次体能测试，测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级，某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析，并根据收集的数据绘制了两幅不完整的统计图，请根据这两幅统计图中的信息回答下列问题
(1)本次抽样调查共抽取多少名学生？
(2)补全条形统计图．
(3)在扇形统计图中，求测试结果为“良好”等级所对应圆心角的度数．
(4)若该学校七年级共有600名学生，请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名？
(5)请你对“不及格”等级的同学提一个友善的建议（一句话即可）．
20．如图，小莹在数学综合实践活动中，利用所学的数学知识对某小区居民楼AB的高度进行测量．先测得居民楼AB与CD之间的距离AC为35m，后站在M点处测得居民楼CD的顶端D的仰角为45︒，居民楼AB的顶端B的仰角为55︒，已知居民楼CD的高度为16.6m，小莹的观测点N距地面1.6m．求居民楼AB的高度（精确到1m）．（参考数。

2024年陕西省西安市铁一滨河中学中考五模英语试题一、完形填空When some people meet difficulties, they always tell themselves “I can’t do it”. Is that right? After a special lesson, I found my answer.One day, our teacher Donna let us 1 a task, filling a piece of paper with something we couldn’t do. We were surprised at first but followed her. A student beside me was filling his page, “I can’t make 2 choice between staying at home and going-out.” I also began my sentences, writing down the things I couldn’t do. Donna also shared the most important things 3 have troubled her, “I can’t get every student interested in reading…”Over the past four weeks, there 4 an increase in the number of “I Can’t”, then our “I Can’t” papers 5 into an empty box. Donna also added hers when all the students put 6 , She took the box and led us to the corner of the playground. “Today we’ll bury our ‘I Can’t!’” Donna said. 7 the hole was about three feet deep, the digging ended. Thirty-one students stood there quietly to see “I Can’t” disappearing in the hole. Some students asked Donna 8 .Donna said that we shouldn’t repeat our “Can’t” because they sometimes stop us 9 moving forward. A more useful way is trying. “I Can’t” should be replaced by “I Cans”, “I Will” and “I’m Going to Do It Right Away”. Maybe someday with our “I Cans”, we will make an ever 10 mark on the world. Therefore, when you face challenges next time, remember to say to yourself “I can” instead of “I can’t”.1．A．finish B．to finish C．collect D．to collect2．A．a B．an C．the D．/3．A．that B．which C．what D．where4．A．has B．has had C．has been D．have been 5．A．puts B．are put C．put D．were put 6．A．they B．them C．their D．theirs 7．A．Though B．Because C．When D．If8．A．why did we do this B．why we did this C．how did we do thisD．how we did this9．A．from B．with C．about D．for10．A．big B．bigger C．close D．closerLong ago, all the birds were invited to a dinner party in the sky. Tortoise heard of the news and asked to join the birds. The birds 11 him at first because he used to be dishonesty and unthankful. However, Tortoise promised to change himself. The birds 12 agreed and they each gave him a feather to make wings.At last, the great day came and they 13 together. Tortoise was so chatty and talkative that the birds chose him to be the spokesperson for the party. Tortoise said people should take new names when they were invited to such a great party. 14 of the birds had known this custom. But they thought Tortoise was widely-travelled and knew the 15 of different places, so each bird took a new name. Tortoise called himself All of You.When all the food was served, Tortoise jumped to his feet and asked, “For 16 have prepared this dinner?”“For all of you,” replied the host.Tortoise 17 the birds and said, “You remember that my name is All of You. The custom here is to serve the spokesperson first and 18 guests later.”He began to eat and ate the best part of the food. The birds had to eat what was left and some of them were too angry to eat. Before they left, each bird took back the feather it had given him.Now, even though Tortoise had no wings, he was so 19 and said: “I can jump down without wings!” And do he did. With a great sound, his shell broke into pieces. The doctor was sent to stick (缝合) the pieces together. This is why a tortoise’s shell is not 20 .What can you learn from the story?11．A．punished B．refused C．accepted D．thanked12．A．finally B．hardly C．actually D．seriously 13．A．put up B．put off C．set up D．set out14．A．All B．None C．Both D．Neither 15．A．history B．habit C．weather D．customs 16．A．what B．which C．whom D．whose 17．A．turned around B．turned to C．turned down D．turned up 18．A．the other B．another C．the others D．others 19．A．sad B．satisfied C．confident D．scared 20．A．pretty B．smooth C．broken D．colorful二、阅读理解It took six hours for Liu Yi, 26, to get to Tianshui, Northwest China’s Gansu province, by train. It took another two hours of waiting in a queue before he could finally get his hands on a bowl of local malatang —a mix of foods boiled in hot, spicy broth*.While choosing the ingredients he wanted, Liu picked wide, thin rice noodles and a lot of chillies, along with the usual vegetables and meat. The malatang did not disappoint. “It has a strong, delicious smell,” Liu said, after he finished his meal.The dish is becoming very popular suddenly. Thousands of diners like Liu have been making their way to the little-known northwestern city to try malatang.These days around 7 am, Li Haiying’s restaurant in Qinzhou district becomes crowded with diners. Earlier, the restaurant would open at 11 am. To serve the increasing number of customers, Li and her family now work from 6:30 am to 10 pm every day. They are too busy to stop for lunch. She said “I have spent so much time improving my cooking skills, and the customers from different cities are often amazed by the taste of the malatang. They think it is so delicious and tastyand I am highly praised by them. But I never boast about my abilities and am always thankful for their praise.”“I have sold malatang for 30 years,” Li said. “I never dreamed that one day it would be so popular.” Recently, over 1,000 customers visit her restaurant each day, even though they might wait around two hours.Ma Yulin, a malatang restaurant owner in the city’s Maiji district, said that over the last 10 days, the restaurant was full of diners, more than half of whom were from other cities. Many young customers not only come to eat but also take photos. Ma has hired more workers and added seats to cut the waiting time.*broth: a kind of soup that is made by boiling meat or fish21．How long did it take Liu Yi to get to Tianshui and finally eat the local malatang?A．6 hours.B．2 hours.C．8 hours.D．4 hours.22．The word “boast” in Paragraph 4 is closest in meaning to “________”.A．look down on B．wonder C．show off D．doubt23．Which of the following is Li Haiying’s opinion on the popularity of malatang?A．She never expected it to become so popular.B．She believes it’s because of her cooking skills.C．She thinks it’s natural for malatang to be popular.D．She’s disappointed with the popularity of malatang.This year, the China Youth and Children Research Center made a report. It said that 30 million Chinese children under the age of 17 are facing a great number of emotional and mind challenges. The mind health of young students has raised the focus from everyone in the whole community. It is a common situation in recent years.Lately, the Education Office and 17 other groups started a plan called “Shared Improvement and Upgrading (提升) of Students’ Mind Health in the New Era (2023—2025)”. The report mentioned, with the quick society and money growth, the world where students grow is always changing quickly. And mind health problems are becoming more common among students. So, a national guidance team on students’ mind health is being created to improve the scientific decision-making about students’ mind health. Work is being done to improve mind health servicesfor students and increase their mind health knowledge.It is understood that this plan aims to fully improve students’ mind health services and increase their mind health knowledge. It has been put into the “Healthy China Action 2023 Work Points”.In my point of view, every student is the future of their family and the community. Taking care of and helping students’ mind health is on the top of a hill of education. By focusing on, assisting, and protecting the mind health of students, we can grow healthy, sound-minded students with endless abilities for all areas of society.24．According to the report, how many Chinese children under 17 are facing emotional and mind challenges?A．10 million.B．20 million.C．30 million.D．40 million. 25．Which of the following is TRUE according to the report?A．The good teaching results are the main task for all schools.B．The national guidance team aims to reduce students’ learning stress.C．The society should pay more attention to students’ physical health.D．The nation is trying to improve mind health services for students.26．The underlined sentence in the last paragraph probably means that ________.A．students should climb the hill bravelyB．students’ mind health is like a hill that is hard to go overC．giving enough love to solve students’ mind health problemsD．students’ mind health should be put in the first place27．The passage ends up with ________.A．the opinion B．a decision C．the fact D．an exampleThe planet’s climate has been changing over thousands of years. The global average temperature today is about 15℃. Scientists are worried that the planet is warming faster than ever before. The 20 warmest years on record have been in the past 22 years, according to the World Meteorological Organization. If this situation continues, temperatures may rise by 3—5℃ by 2100.Scientists say we should try to make the present situation come to a stop and not allow theglobal average temperature to rise more than 1.5℃. Even a 2℃ rise would be bad for us all. Now, half a degree doesn’t sound like much—but it could make a big difference to the planet.A 2℃ rise would mean that all the coral reefs (珊瑚礁) would disappear, but a 1.5℃ rise means that there would still be some. Also, 18 percent of the insects on Earth will disappear if the temperature goes up by 2℃, compared to 6 percent disappearing at 1.5℃. A 2℃ rise would also mean that 37 percent of people will be influenced by dangerous heatwaves. That’s twice the number compared to at a 1.5℃ rise. Do you want to know what scientists say? They say that everyone and everything is far better off in a world that limits the rise to 1.5℃.So, what can we do? Please return to us in our magazine next month, you will read about the advice given by the world’s top scientists, researchers and leading environmental protectors. We’d also like to hear about your ideas and suggestions. Please write to us at **************************.uk.Let’sworktogethertolimitthetemperatureriseto1.5℃. 28．According to the first paragraph, we can know that ________.A．the planet is the warmest this yearB．the average temperature today is 1.5℃ in ChinaC．the planet’s climate has the biggest change this yearD．the temperatures may rise to 18—20℃ by 210029．What will happen with a 2℃ rise?a. All the coral reefs will disappear.b. Half of the planet will be influenced.c.18 percent of the insects on Earth will disappear.d. 37 percent of people will be influenced by dangerous heatwaves.A．abc B．bcd C．acd D．abd30．How can you complete the title for the passage; Climate Change: ________?A．What Can We Do B．How Does It HappenC．Why Is 1.5℃ Important D．How Does It Influence Our LivesSmartphones are getting boring. The new models are either a bit faster or have better cameras, but they are nearly no different from the ones already in our pockets. This is why scientists are hoping and working for something new, something that will change our lives just asgreatly as smartphones do. 31 .Just imagine. Instead of having to pick up your phone, all of the information you need simply appears just in your glasses. Satellite navigation (导航) directions would appear right there on the road. And your smart glasses could guide you to the right shelf in the supermarket!32 . They could show engineers the instructions they need to fix things more quickly.A doctor could carry out a difficult operation, guided in real time by someone on the other side of the world.33 . But most of the technologies to invent them are already there. For example, one key technology is called AR, which can make digital 3D objects appear as if they are part of the real world. 34 . Future glasses will of course need to recognize your voice to do tasks. This technology has been widely used in our daily life.So, why aren’t we all wearing smart glasses that can see the images yet? 35 .However, with the rapid development of technology, smart glasses could arrive much sooner than we think.A．Smart glasses could also be used in industryB．We’ve used AR a lot on our video callsC．At the moment, the next invention might be smart glassesD．And the technology is also very importantE．This may sound impossibleF．Smart glasses is used in very few fieldsG．So far, no one has invented a good way to send images of our world onto glasses三、完成句子36．远亲不如近邻。

【初2024届】中考适应性训练试题（五）物理（满分：80分时长：75分钟g取10N/kg）一、选择题（共10小题，每小题2分，计20分，每小题只有一个选项是符合题意的）1. 2024年央视春晚西安分会场的《山河诗长安》大放异彩，“出圈”走红，其中数字人“李白”的动作捕捉采用了目前最贵的光学动作捕捉技术，其原理是利用多个红外摄像机固定在一个室内空间中。

根据空间大小以及捕捉的人数来确定摄像机的数量，光学的优点就是精度高，缺点是价格昂贵、操作复杂、需要固定场地等。

针对节目中所示涉及的物理知识，下列说法中正确的是（ ）A. 李白和张若昀饰演的范闲之间的“梦幻联动”，用到的摄像机成倒立放大的虚像B. 拟音“对诗”，模仿的主要是音色C. “李白弹琵琶”按压不同位置，改变的是声音的响度D. 数字人“李白”身着动捕服，采集动作运用是超声波的2. 光给我们的生活带来了缤纷色彩，如图所示，对光现象的分析中说法正确的是（ ）A. 图-1，小孔所成像原理是由于光的反射B. 图-2，将纸板NOF 沿NO 向后折时看不到反射光线，原因是这时没有反射光线C. 图-3，体温计玻璃管读数部分截面做成圆弧状，利用凸透镜成正立放大虚像的原理D. 图-4，要使投影仪成像变大，应使投影仪靠近屏幕，同时使镜头远离胶片3. 物理学是一门以实验为基础学科，对于下列实验中的物理过程，说法正确的（ ）A. 图-1，塑料绳因摩擦其下端带同种电荷而分开，说明通过摩擦可以创造电荷B. 图-2，活塞迅速下压过程中其能量转化与汽油机做功冲程相同C. 图-3，扩散实验说明分子在永不停息的做无规则运动D. 图-4，左边肥皂膜戳破后棉线被拉向右边，说明分子间存在着引力，没有斥力4. “科技冬奥”带动起了5G、氢能出行、智能车联网、能源及可持续发展等重大高新技术，为经济社会的的高质量发展发挥积极作用，下列说法正确的是（ ）A. 生物质能主要取自于柴薪、农作物秸秆、牲畜粪便等，是地球上最丰富的可再生能源B. 5G网络速度比4G更快，因为它们电磁波的传播速度不一样C. 自然界中许多自发的过程都是有方向的，而能量的转移和转化没有方向D. 电视广播、移动通讯用微波传递信号，三颗地球同步卫星均匀分布无法实现全球覆盖5. 物理新课程标准注重“知行合一，学以致用”的课程理念，以具体事实、鲜活案例、生活经验和基本概念引导学生理性思考。

2024年陕西省西安市铁一中学（曲江校区）中考五模物理试题一、单选题1．校园生活，同学们并不陌生，下列有关说法最合理的是（）A．操场篮球架上的篮圈距地面的高度约为5mB．此时教室内的温度约为42CC．微机室内台式计算机的功率约为300WD．普通乒乓球拍的质量约为2kg2．如图是我校“胸怀泼云志，砥砺勇攀登”活动开幕式的情景，慷慨激昂的鼓声使同学们热血沸腾，下列说法不正确的是（）A．鼓声是由鼓面振动产生的B．用力敲击鼓面是为了增大响度C．快速敲击鼓面时，频率越高，音调越高D．鼓声越大，在空气中传播的速度越大3．如图为西安古城墙永宁门的灯光秀，给广大西安市民和外地游客带来了光的盛宴。

下列关于灯光秀的说法正确的是（）A．我们看到各种光源发出的光在空中沿直线传播，这就是我们常说的“光线”B．晚上天空中五颜六色的光是由光的色散形成的C．当红色灯光照在白色的衣服上时，我们看到衣服是白色的D．我们能从不同角度看到美轮美奂的古城墙盛景，是因为光在城墙表面发生的是漫反射4．冬天，“尔滨”凭借冰雪大世界在国内外火出圈。

某游客游玩时记录下了下列四个场景，其中说法正确的是（）A．图-1，早市上可看到各个摊位向上冒“白气”，“白气”是水蒸气B．图-2，街边的树枝上挂满了针状“雾凇”，针状“雾凇”是水凝华形成的C．图-3，松花江上惊现“雪人群”，造“雪人群”的雪是晶体D．图-4，玻璃窗上出现了美丽的“冰窗花”，“冰窗花”的形成需要吸热5．2024年4月试通车的西安高新有轨电车是西安首条采用云巴模式建设的轨道交通系统具有速度大.污染小的优点。

当电车运行时，由于高速摩擦，在电车跟架空电线的接触点上会产生高温。

因此，接触点上的材料应该具有耐高温，不易氧化，易导电的性质，最适合制作该触电的材料是（）A．金刚石B．石墨C．铝D．铜6．掷实心球是南充中考体育项目之一，如图所示是某同学掷出的实心球的运动轨迹，O点是实心球刚离开手的位置，A点是实心球运动到最高点的位置，B点是实心球落地前瞬间的位置，不计空气阻力，下列说法正确的是（）A．实心球离开手后受到重力和惯性力的作用B．实心球在最高点A时处于平衡状态C．实心球从O运动到B的动能先减小后增大D．实心球在O点的机械能大于在B点的机械能7．生活中，我们应“珍爱生命，规范用电”。

一、选择题（每题3分，共30分）1. 下列数中，是正整数的是（）A. -5B. 0.5C. 2D. -22. 已知a=3，b=-2，则a²+b²的值为（）A. 1B. 5C. 7D. 93. 在直角坐标系中，点A（2，3）关于y轴的对称点是（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）4. 下列函数中，是反比例函数的是（）A. y=x²B. y=2xC. y=2/xD. y=3x+25. 一个长方形的长是a，宽是b，则它的周长S=（）A. 2a+2bB. a+bC. 2aD. 2b6. 下列数中，是质数的是（）A. 18B. 23C. 24D. 297. 在△ABC中，∠A=45°，∠B=60°，则∠C的度数是（）A. 45°B. 60°C. 75°D. 90°8. 下列等式中，正确的是（）A. (a+b)²=a²+b²B. (a-b)²=a²-b²C. (a+b)²=a²+2ab+b²D. (a-b)²=a²-2ab+b²9. 已知x+y=5，x-y=1，则x²+y²的值为（）A. 10B. 15C. 16D. 2010. 下列图形中，是轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 平行四边形二、填空题（每题5分，共25分）11. 若a²=9，则a=__________。

12. 在直角坐标系中，点P（-1，2）关于原点的对称点是__________。

13. 一次函数y=kx+b的图象与x轴、y轴的交点分别是（0，b）和（-b/k，0），若图象经过点（1，-3），则k=__________，b=__________。

14. 若一个数的平方根是2，则这个数是__________。

2020年陕西省西安市碑林区铁一中学中考数学五模试卷一、选择题（本大题共10小题，共30.0分）1.3的平方根是()A. 9B. ±9C. √3D. ±√32.鲁班锁，民间也称作孔明锁，八卦锁，它起源于中国古代建筑中首创的榫卯结构．如图是鲁班锁的其中一个部件，它的左视图是()A. B. C. D.3.将一副三角板和一张对边平行的纸条(a//b)按如图摆放，则∠1的度数是()A. 15°B. 22.5°C. 30°D. 45°4.下列计算正确的是()A. 2a2⋅3a2=6a2B. (−3a2b)3=9a6b3C. (a+b)2=a2+b2D. −a2+2a2=a25.正比例函数y=kx(k≠0)的图象经过点P，若点P在第二象限，且P到x轴的距离为1，到y轴的距离为3.则k的值为()A. 3B. −13C. −3 D. 136.在等腰△ABC中，AB=AC，D、E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在△ABC的()A. 重心B. 内心C. 外心D. 不能确定7.如图，在矩形OABC中，点B的坐标是(1,3)，则A、C两点间的距离是()A. 4B. √13C. √10D. 2√28. 若直线y =3x +m 和y =nx −4相交于点P(−3,−2)，则方程组{y =3x −my =nx +4的解为( )A. {x =−3y =−2B. {x =−3y =2C. {x =3y =−2D. {x =3y =29. 如图，四边形ABCD 内接于⊙O ，DA =DC ，∠CBE =50°，∠AOD 的大小为( )A. 130°B. 100°C. 120°D. 110°10. 已知两点A(−5,y 1)，B(−1,y 2)均在抛物线y =ax 2+bx +c(a ≠0)上，点C(x 0,y 0)是该抛物线的顶点，若y 1>y 2≥y 0，则x 0的取值范围是( )A. x 0>−5B. x 0>−1C. x 0>−3D. −5<x 0<−1二、填空题（本大题共4小题，共12.0分）11. 截至格林尼治标准时间2020年6月7日10时，全球累计报告新冠肺炎确诊病例达7000000例；其中累计死亡病例超过40万例，数据7000000科学记数法表示为______． 12. 在一个边长为a 正方形的四个角上各裁去一个等腰直角三角形后，得到了一个边长为b 的正八边形，则ab 的值为______．13. 如图，在平面直角坐标系中，反比例函数y =kx (k >0)的图象经过平行四边形ABCD 的顶点C 、D ，若点A 、B 的坐标分别为(3,0).(0,4)，点C 的横坐标和纵坐标之和为152，则k 的值为______．14. 如图，在正方形ABCD 中，E 是对角线AC 上的动点，以DE 为边作正方形DEFG ，H 是CD 的中点．连接GH ，若GH 的最小值是1，则正方形ABCD 的边长为______．三、计算题（本大题共2小题，共12.0分）15.计算：2−1+√12−6tan30°−(−2020)0．16.如图，小明想用所学的知识来测量长安塔的高度，他先在E处用侧倾器测得塔顶A的仰角α为30°，然后，他从E处迎着塔的方向走了71.1米到F处，再用侧倾器测得塔顶A的仰角β为45°，已知点E、F、B在同一水平面上，侧倾器的高度为1.6米，请你利用小明测得的相关数据，求长安塔的高度AB(结果精确到1米．参考数据：√2≈1.41，√3≈1.73)四、解答题（本大题共9小题，共66.0分）17.化简(a−ba+b +4aba2−b2)÷a+ba2−ab．18.如图，请用尺规作图法过点A求作一条直线AB，使得直线AB将该圆分成相等的两部分．(保留作图痕迹，不写作法)19.已知：如图，在矩形ABCD中，∠CAB、∠ACD的平分线AE、CF分别交BC、AD于点E、F.求证：AE=CF．20.某学校在“预防感染新型冠状病毒”培训学习后，为了了解同学们对预防新冠知识的掌握状况，对同学们进行随机抽样调查，并对调查结果进行统计，掌握状况划分为四个等级：A优秀，B良好，C合格，D不合格，如图所示．请结合统计图回答下列问题：(1)该校抽样调查的学生人数为______．(2)请补全条形统计图．(3)该校共有学生1800人，试估计全校测试成绩为优秀和良好的学生共有多少人．21.聚焦三农，脱贫攻坚，响应习主席小木耳大市场的倡导，小李家的网店将A、B两种木耳进行销售，A和B这两种规格木耳的相关信息如下表根据上表提供的信息，解答下列问题：(1)已知今年五月份，小李家网店销售A和B两种木耳共875kg，获得利润6.6万元，求今年五月份小李家网店销售A和B两种木耳各多少袋；(2)根据之前的销售情况，估计今年六月份，小李家网店还能销售A和B两种木耳共800kg，其中A木耳的销售量不低于300kg，假设六月份销售A木耳x(kg)，销售A和B两种木耳获得的总利润为y(元)，求出y与x之间的函数关系式，并求出六月份小李家网店销售A和B两种木耳至少获得总利润多少元．22.现有同一副扑克牌中的2张“方块”，3张”梅花”，1张“红桃”，将这6张牌背面朝上洗匀，放置在水平桌面．(1)从中随机抽取1张，是“方块”的概率为______．(2)先从中随机抽取一张，再从剩下的牌中随机抽取一张．请用树状图或列表法求抽中的两张中“一张是梅花，一张是红桃”的概率．23.如图△ABO中，AB=12，OA=13，OB=5，以O为圆心，OB为半径的⊙O交OA于C.过点C作弦CD//OB．(1)求证：AB与⊙O相切；(2)求弦CD的长．24.如图抛物线经过点A(−6,0)，B(−2,0)，C(0,3)，点D为该抛物线的顶点．(1)求该抛物线的解析式和点D坐标；(2)在该抛物线的对称轴上是否存在点P，且在该抛物线上是否存在点Q，使得以A、C、P、Q为顶点的四边形是平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．25.问题提出(1)如图①，在△ABC中，∠B=90°，∠A=60°，BC=4，则△ABC的面积为______．问题探究(2)如图②，在△ABC中，∠A=60°，BC=4，求△ABC面积的最大值．问题解决(3)如图③所示，ABCDE为一个钢架结构的五边形工件，其中△ABE部分由某种合金材料制成，根据设计要求，CD=40cm，AB：BC=AE：DE=√3：1，∠BAE=120°，∠ABC=∠AED=90°，若不计损耗，请求出需要准备这种合金材料的最大面积．答案和解析1.【答案】D【解析】解：实数3的平方根是±√3．故选D．根据平方根的定义，即可解答．本题考查了平方根，解决本题的关键是熟记平方根的定义．2.【答案】D【解析】解：从左边看，是一个矩形，矩形的中间有一条横向的虚线．故选：D．根据从左边看得到的图形是左视图，可得答案．本题考查了简单组合体的三视图，从左边看得到的图形是左视图．3.【答案】A【解析】解：如图，∵a//b，∴∠2=∠4=30°，∴∠1=∠3−∠2=45°−30°=15°．故选：A．延长两三角板重合的边与直尺相交，根据两直线平行，内错角相等求出∠2，再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．本题考查了平行线的性质，三角板的知识，熟记平行线的性质，三角板的度数是解题的关键．4.【答案】D【解析】解：A、2a2⋅3a2=6a4，故此选项错误；B、(−3a2b)3=−27a6b3，故此选项错误；C、(a+b)2=a2+2ab+b2，故此选项错误；D、−a2+2a2=a2，正确．故选：D．直接利用积的乘方运算法则以及完全平方公式、合并同类项法则、整式乘法运算法则分别计算得出答案．此题主要考查了整式的混合运算，正确掌握相关运算法则是解题关键．5.【答案】B【解析】解：∵点P在第二象限，且P到x轴的距离为1，到y轴的距离为3，∴点P的坐标为(−3,1)．∵正比例函数y=kx(k≠0)的图象经过点P，∴1=−3k，∴k=−1．3故选：B．由点P所在的象限及到两坐标轴的距离，可得出点P的坐标，再利用一次函数图象上点的坐标特征，即可得出关于k的一元一次方程，解之即可得出k值．本题考查了一次函数图象上点的坐标特征，由点P所在的象限及到两坐标轴的距离，确定点P的坐标是解题的关键．6.【答案】A【解析】解：取AB的中点F，连接EF，连接CF交AD于P′，如图，∵E点为AC的中点，∴EF为△ABC的中位线，∴EF//BC，∵AB=AC，点D为BC的中点，∴AD⊥BC，∴AD⊥EF，AB，∵AE=AF=12∴AD垂直平分EF，∴P′E=P′F，∴P′C+P′E=P′C+P′F=CF，∴此时P′C+P′E的值最小，△P′CE的周长最小，而P′点为△ABC的中线AD和CF的交点，即P′点为△ABC的重心．故选：A．取AB的中点F，连接EF，连接CF交AD于P′，如图，先判断EF为△ABC的中位线得到EF//BC ，再根据等腰三角形的性质得到AD ⊥BC ，接着判断AD 垂直平分EF ，则P′E =P′F ，然后利用两点之间线段最短判断此时P′C +P′E 的值最小，△P′CE 的周长最小，根据三角形重心的定义得到P′点为△ABC 的重心．本题考查了三角形的重心：三角形的重心是三角形三边中线的交点．重心到顶点的距离与重心到对边中点的距离之比为2：1.也考查了等腰三角形的性质．7.【答案】C【解析】解：在矩形OABC 中， OB =AC ， ∵B(1,3)，∴OB =√12+32=√10， 故选：C ．根据矩形的性质即可求出答案．本题考查矩形，解题的关键是熟练运用矩形的性质以及勾股定理，本题属于基础题型．8.【答案】D【解析】解：直线y =3x +m 和y =nx −4关于原点对称的直线为y =3x −m 和y =nx +4，∵直线y =3x +m 和y =nx −4相交于点P(−3,−2)， ∴直线y =3x −m 和y =nx +4相交于点(3,2)， ∴方程组{y =3x −m y =nx +4的解为{x =3y =2，故选：D ．求得直线y =3x +m 和直线y =nx −4关于原点对称的直线，由题意得出点P 的对应点，根据方程组的解和直线交点的关系即可求得．本题考查了对一次函数与二元一次方程组的关系的理解和运用，题目比较典型，求得直线关于原点的对称直线是解题的关键．9.【答案】A【解析】解：∵∠ADC +∠ABC =180°，∠ABC +∠CBE =180°， ∴∠ADC =∠CBE =50°， ∵DA =DC ，∴∠DAC=∠DCA=1(180°−50°)=65°，2∴∠AOB=2∠ACD=130°，故选：A．首先证明∠ADC=∠CBE，再利用等腰三角形的性质求出∠ACD，利用圆周角定理即可解决问题．本题考查圆内接四边形的性质，等腰三角形的性质，圆周角定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．10.【答案】C【解析】解：∵两点A(−5,y1)，B(−1,y2)均在抛物线y=ax2+bx+c(a≠0)上，点C(x0,y0)是该抛物线的顶点，∴若y1>y2≥y0，则此函数开口向上，有最小值，<x0≤−1或x0≥−1，∴−5−12解得，x0>−3故选：C．根据二次函数的性质可知该函数开口向上，有最小值，从而可以求得x0的取值范围．本题考查二次函数的性质、二次函数图象上点的坐标特征，解答本题的关键是明确题意，找出所求问题需要的条件，利用二次函数的性质解答．11.【答案】7×106【解析】解：7000000科学记数法表示为：7×106．故答案为：7×106．根据科学记数法形式：a×10n，其中1≤a<10，n为正整数，即可求解．本题考查了科学记数法，解决本题的关键是把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，n是正整数，这种记数法叫做科学记数法．[科学记数法形式：a×10n，其中1≤a<10，n为正整数．]12.【答案】√2+1【解析】解：如图所示：BD=BE=b，AB+BD+CD=a设AB=AE=CD=c．则由题意，得2c+b=a，b=√2c.∴ab=2c+bb=2c+√2c √2c=√2+1．根据勾股定理和线段的和差关系，用等腰直角三角形的直角边分别表示出正方形的边长和正八边形的边长，再求值即可．本题考查了正方形、等腰直角三角形、正八边形的性质，利用直角等腰三角形的边长表示出正方形和正八边形的边长，是解决本题的关键．13.【答案】9【解析】解：∵点C的横坐标和纵坐标之和为152，∴设C(a,152−a)，设D的坐标为(m,n)，∵四边形ABCD是平行四边形，∴BA//CD，BA=CD，∵A(3,0)，B(0,4)，∴m−a=3−0，n−(152−a)=0−4，∴m=a+3，n=72−a，∴D(a+3,72−a)，∵C、D两点都在反比例函数y=kx(k>0)的图象上，∴k=a(152−a)=(a+3)(72−a)，解得，a=32，∴k=32×(152−32)=9，故答案为：9．设C(a,152−a)，根据平行四边形求得D点的坐标，再根据C、D两点都在反比例函数y=kx(k>0)的图象上，列出a的方程，求得a，再求k便可．本题主要考查了平行四边形的性质，反比例函数的图象与性质，关键是正确表示用一个字母表示C、D点的坐标．14.【答案】2√2【解析】解：连接CG．∵四边形ABCD是正方形，四边形DECG是正方形，∴DA=DC，DE=DG，∠ADC=∠EDG=90°，∠DAC=45°，∴∠ADE=∠CDG，∴△ADE≌△CDG(SAS)，∴∠DCG=∠DAE=45°，∴点G的运动轨迹是射线CG，根据垂线段最短可知，当GH⊥CG时，GH的值最小为1，∴CH=GHsin45∘=√22=√2．∴CD=2CH=2√2，故答案为：2√2．连接CG.证明△ADE≌△CDG(SAS)，推出∠DCG=∠DAE=45°，推出点G的运动轨迹是射线CG，根据垂线段最短可知，当GH⊥CG时，GH的值最小，再解直角三角形求得CH，便可得正方形ABCD的边长．此题考查正方形的性质，全等三角形的性质与判定，解直角三角形的应用，垂线段最短性质，关键是根据垂线段最短性质确定GH最小值的位置．15.【答案】解：2−1+√12−6tan30°−(−2020)0=12+2√3−6×√33−1=12+2√3−2√3−1=−12．【解析】根据负整数指数幂、特殊角的三角函数值、零指数幂可以解答本题．本题考查实数的运算、负整数指数幂、特殊角的三角函数值、零指数幂，解答本题的关键是明确它们各自的计算方法．16.【答案】解：设CD延长线于AB交于点G，根据题意可知：四边形GBEC、四边形GBFD、四边形DFEC是矩形，∴BG=DF=CE=1.6，DC=EF=71.1，DG=BF，∵∠ADG=45°，∴AG=DG=BF，设AG=DG=BF=x，在Rt△ACG中，∠ACG=30°，AG=x，CG=DG+DC=x+71.1，∴tan30°=AGCG，即√33=xx+71.1，解得x≈97.1，∴AB=AG+GB=97.1+1.6≈99(米)．答：长安塔的高度AB约为99米．【解析】设CD延长线于AB交于点G，根据题意可得四边形GBEC、四边形GBFD、四边形DFEC是矩形，可得BG=DF=CE=1.6，DC=EF=71.1，DG=BF，再根据特殊角三角函数即可求出长安塔的高度AB．本题考查了解直角三角形的应用−仰角俯角问题，解决本题的关键是掌握仰角俯角定义．17.【答案】解：(a−ba+b +4aba2−b2)÷a+ba2−ab=(a−b)(a−b)+4ab(a+b)(a−b)⋅a(a−b)(a+b) =a2−2ab+b2+4aba+b⋅aa+b =(a+b)2a+b⋅aa+b=a．【解析】根据分式的加法和除法可以解答本题．本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法．18.【答案】解：如图所示：．【解析】根据题意可得，以A为圆心，任意长为半径与圆交于两点，在分别以这两个点为圆心，大于1这两点的距离为半径作弧，交于一点，然后连接点A和最后的交点，即2可将圆分为相等的两部分．本题考查作图−复杂作图，解答本题的关键是明确题意，画出相应的图形．19.【答案】证明：∵四边形ABCD是矩形，∴AF//CE，AB//CD，∴∠BAC=∠DCA，又∵∠CAB、∠ACD的平分线AE、CF分别交BC、AD于点E、F，∴∠EAC=∠FAC，∴AE//CF，又∵AF//CE，∴四边形AECF是平行四边形，∴AE=CF．【解析】根据矩形的性质，可以得到AF//CE，AB//CD，从而可以得到∠BAC=∠DCA，再根据平角平分线的性质，可以得到∠EAC=∠FAC，从而可以得到AE//CF，然后即可得到四边形AECF是平行四边形，从而可以得到AC=CF．本题考查矩形的性质、平行四边形的判定和性质，解答本题的关键是明确题意，利用数形结合的思想解答．20.【答案】50【解析】解：(1)该校抽样调查的学生人数为：16÷32%=50(人)， 故答案为：50；(2)B 等级的人数为：50−16−10−4=20(人)，补全的条形统计图如右图所示； (3)1800×16+2050=1296(人)，答：全校测试成绩为优秀和良好的学生共有1296人．(1)根据A 等级的人数和所占的百分比，可以求得本次调查的人数；(2)根据(1)中的结果和条形统计图中的数据，可以计算出B 等级的人数，从而可以将条形统计图补充完整；(3)根据条形统计图中的数据，可以计算出全校测试成绩为优秀和良好的学生共有多少人．本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．21.【答案】解：(1)设销售A 种木耳x 袋，B 种木耳y 袋，由题意得，{250x +500y =875000(122−98)x +(190−160)y =66000， 解得，x =1000，y =1250，答：今年五月份小李家网店销售A 种木耳1000袋，B 种木耳1250袋． (2)由题意得， y =(122−98)x 0.25+(190−160)800−x 0.5=36x +48000，∴y 随x 的增大而增大， ∵x ≥300，当x =300时，y 最小=36×300+48000=58800元，答：y 与x 之间的函数关系式为y =36x +48000，六月份小李家网店销售A 和B 两种木耳至少获得总利润多少元58800元．【解析】(1)设未知数，列二元一次方程组解答即可；(2)根据利润与销售量的关系，得出y 与x 之间的函数关系式，再根据函数的增减性，得出何时利润最少．考查二元一次方程组解法及其应用，一次函数的性质等知识，正确的得到函数关系式是解决问题的关键．22.【答案】13【解析】解：(1)∵共有6张扑克牌，分别是2张“方块”，3张”梅花”，1张“红桃”，∴从中随机抽取1张，是“方块”的概率为26=13；故答案为：13；(2)根据题意列表如下：共有30种等可能的情况数，其中抽中的两张中“一张是梅花，一张是红桃”有6种，则抽中的两张中“一张是梅花，一张是红桃”的概率是630=15．(1)直接根据概率求解即可；(2)根据题意列出图表得出所有等情况数，找出符合题意的情况数，然后根据概率公式即可得出答案．此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．23.【答案】解：(1)∵AB=12，OA=13，OB=5，∴OA2=OB2+AB2，∴∠ABO=90°，∵OB是⊙O的半径，∴AB与⊙O相切．(2)过点O作OE⊥CD于点E，∵CD//OB，∴∠ECO=∠AOB，∴cos∠ECO=cos∠AOB=513，∵OC=OB=5，CEOC =513，∴CE=2513，∴由垂径定理可知：CD=2CE=5013．【解析】(1)根据勾股定理的逆定理以及切线的判定即可求出答案．(2)过点O作OE⊥CD于点E，由题意可知cos∠ECO=cos∠AOB=513，OC=5，根据锐角三角函数的定义即可求出答案．本题考查圆的综合问题，涉及切线的性质，勾股定理，锐角三角函数等知识，需要学生灵活运用所学知识．24.【答案】解：(1)设抛物线解析式为：y=a(x+6)(x+2)，由题意可得：3=12a，∴a=14，∴抛物线解析式为：y=14(x+6)(x+2)=14x2+2x+3；(2)∵点A(−6,0)，B(−2,0)，∴对称轴为x=−6−22=−4，∴设点P(−4,m)，点Q(x,14x2+2x+3)，若以AC为边，AP为边，∵以A、C、P、Q为顶点的四边形是平行四边形，∴CP与AQ互相平分，∴−4+02=−6+x2，∴x=2，∴点Q(2,8)；若以AC为边，CP为边，∵以A、C、P、Q为顶点的四边形是平行四边形，∴AP与CQ互相平分，∴−6−42=x+02，∴x=−10，∴点Q(−10,8)；若AC为对角线，∵以A、C、P、Q为顶点的四边形是平行四边形，∴AC与PQ互相平分，∴−6+02=−4+x2，∴x=−2，∴点Q(−2,0)；综上所述：点Q坐标为(2,8)或(−10,8)或(−2,0)．【解析】(1)设抛物线解析式为：y=a(x+6)(x+2)，将点C坐标代入可求解；(2)分两种情况讨论，利用平行四边形的性质和中点坐标公式可求解．本题是二次函数综合题，考查了二次函数的性质，待定系数法求解析式，平行四边形的性质，中点坐标公式，利用分类讨论思想解决问题是本题的关键．25.【答案】8√33【解析】解：(1)∵∠B=90°，∠A=60°，∴∠A=30°，∴BC=√3AB=4，∴AB=4√33，∴△ABC的面积=12×AB×BC=12×4√33×4=8√33，故答案为：8√33．(2)如图②，作△ABC 的外接圆O ，作BC 的垂直平分线交⊙O 于A ，交BC 于E ，此时△ABC 的面积最大，连接OB ，OC ，∵OB =OC ，∴点O 在BC 的垂直平分线上，∠OBC =∠OCB ， ∵∠BOC =2∠BAC =120°， ∴∠OBC =∠OCB =30°， 又∵OE 垂直平分BC ，∴BE =CE =12BC =2，BO =2OE ，BE =√3OE ， ∴OE =2√33，BO =AO =4√33， ∴AE =OE +AO =2√3，∴△ABC 的最大的面积=12×4×2√3=4√3；(3)如图，过点B 作BF ⊥AE 交EA 的延长线于F ，连接AC ，过点C 作CH ⊥AD 于H ，∵AB ：BC =AE ：DE =√3：1，∴设AB =√3a ，BC =a ，AE =√3b ，DE =b ， ∵∠ABC =∠AED =90°， ∴tan∠BAC =BCAB =√33，tan∠DAE =DEAE =√33， ∴∠BAC =30°=∠DAE ， ∵∠BAE =120°，∴∠BAF =60°，∠CAD =60°， ∵BF ⊥AF ，∴∠ABF=30°，∴AF=12AB=√32a，BF=√3AF=32a，∴S△ABE=12AE×BF=3√34ab，∵AB=√3a，BC=a，∴AC=√AB2+BC2=√3a2+a2=2a，同理可得AD=2b，∵sin∠CAH=sin60°=CHAC =√32，∴CH=√3a，∴S△ACD=12AD×CH=12×2a×√3b=√3ab，∴ab=√33S△ACD，∴S△ABE=3√34ab=3√34×√33S△ACD=34S△ACD，∴当S△ACD取最大值时，S△ABE有最大值，由(2)可知：S△ACD最大值为400√3，∴S△ABE最大值为300√3．(1)由直角三角形的性质先求出AB的长，由三角形面积公式可求解；(2)作△ABC的外接圆O，作BC的垂直平分线交⊙O于A，此时△ABC的面积最大，由圆周角定理可求∠BOC=2∠BAC=120°，可得∠OBC=∠OCB=30°，由等腰三角形的性质可得OE，OB，OA的长，即可求解；(3)过点B作BF⊥AE交EA的延长线于F，过点C作CH⊥AD于H，连接AC，分别求出S△ABE=12AE×BF=3√34ab，S△ACD=12AD×CH=√3ab，可得S△ABE=3√34ab=3√3 4×√33S△ACD=34S△ACD，则当S△ACD取最大值时，S△ABE有最大值，由(2)可得S△ACD最大值为400√3，即可求解．本题是三角形综合题，考查了直角三角形的性质，圆的有关知识，锐角三角函数等知识，利用参数表示三角形的面积是本题的关键．第21页，共21页。

2023年陕西省西安市铁一中学中考五模英语试题学校:___________姓名：___________班级：___________考号：___________一、完形填空阅读下面短文，按照句子结构的语法性和上下文连贯的要求，从所给的四个选项中选出一个最佳答案，使短文连贯完整。

As soon as I got home from school, Aunt Beth noticed the silver medal hanging from the left pocket of my uniform. She 1 her hair in front of the mirror in our room when I walked in and put my school bag down on my bed.“What’s that hanging on your dress?”“It’s 2 that Mother Agnes gave me in front of the whole class this afternoon.”My aunt looked 3 . “So soon? You started school only one week ago. What is it 4 ?”“It’s because I topped my class this week. Mother Agnes said I could wear it for seven days. Here, this certificate（证书）goes with it.” I opened my schoolbag and handed her the certificate.“Why, it’s all 5 in French or English or some other foreign languages. How do you expect me 6 this?” I knew she was glad because she was smiling as she hugged me. “One day soon,” she went on, “you’ll be able to translate all this into Chinese for me.7 then, we’ll just write today’s date on the certificate and 8 . Go and close the door so no one will come in.”I watched her go to the bookcase and take out 9 wooden box. She took the key, opened the box and placed my certificate under her diamond watch. In her eyes, my certificate was 10 the watch.1．A．brushes B．brushing C．was brushing D．brushed 2．A．special something B．something special C．special anythingD．anything special3．A．boring B．bored C．exciting D．excited 4．A．with B．in C．on D．for 5．A．writing B．wrote C．writes D．written 6．A．read B．to read C．reading D．reads 7．A．While B．Although C．Until D．If8．A．put it away B．put away it C．put them away D．put away them 9．A．/B．a C．an D．the 10．A．as important as B．more important C．the most important D．important阅读下面一篇短文，理解大意，然后从各小题的四个选项中选出一个最佳答案，使短文连贯完整。

2022年陕西省西安市灞桥区铁一中滨河学校中考数学五模试卷1. 计算(−2)0=( )A. 0B. 1C. −1D. −22. 某几何体由一些大小相同的小正方体组成，如图是它的俯视图和主视图，那么组成该几何体的小正方体的个数最少为( )A. 4个B. 5个C. 6个D. 7个3. 计算1a−b −aa2−b2的结果为( )A. ba2−b2B. ba−bC. bD. −b4. 如图所示，直线a//b，∠2=28°，∠1=50°，则∠A=( )A. 32°B. 78°C. 22°D. 20°5. 一次函数y=(m−2)x+m+3的图象如图所示，则m的取值范围是( )A. m>2B. m<2C. 2<m<3D. −3<m<26. 如图，在四边形ABCD中，E，F分别是AD，BC的中点，G，H分别是对角线BD，AC的中点，依次连接E，G，F，H，连接EF，GH，BD与EH相交于P，若AB=CD，∠ABD=20°，∠BDC= 70°，则∠GEF=度．( )A. 25B. 30C. 45D. 357. 在平面直角坐标系中，将抛物线C：y=2x2−(m+1)x+m绕原点旋转180°后得到抛物线C′，在抛物线C′上，当x<1时，y随x的增大而增大，则m的取值范围是( )A. m≥5B. m≤5C. m≥−5D. m≤−58. 不等式5x−2>3的解集为______．9. 已知扇形的弧长为2πcm，半径为4cm，则此扇形的面积为______cm2．10. 如图，AD是正五边形ABCDE的一条对角线，以C为圆心，CB为半径画弧交AD于点F，连接CF，则∠CFD=°.11. 符合黄金分割比例形式的图形很容易使人产生视觉上的美感．如图所示的五角星中，AD=BC，且C、D两点都是AB的黄金分割点，若CD=1，则AB的长是______．12. 如图，直线y=−1x+2与x，y轴交于A、B两点，以AB2为边在第一象限作矩形ABCD，矩形的对称中心为点M，若(x>0)恰好过点C、M，则k=______ ．双曲线y=kx13. 在△ABC中，AB=4，∠C=45°，则√2AC+BC的最大值为______．14. 计算：(−1)−2+(2022−π)0−|√8−2|+2sin45°．315. 计算：(a +1)(a −3)−(a −2)2．16. 解方程组：{x 3+1=y(1)2(x +1)−y =6(2)． 17. x+1x−1−1=4x 2−1．18. 请利用尺规作图在△ABC 的AB 、AC 边上分别找点M 、点N ，连接MN ，使得S △AMN =14S △ABC (保留作图痕迹，不写作法)．19. 如图，在平行四边形ABCD 中，对角线AC 的垂直平分线分别与边AB 和边CD 的延长线交于点M ，N ，垂足为点O.求证：BM =DN ．20. 甲、乙两人同时从A 地到B 地，甲骑摩托车，乙骑自行车．甲、乙时速之比为5：1，甲先到达B 地以后立即返回A 地．在返回途中遇见乙，此时，距他们出发时间为2小时15分．若A 地、B 地相距67.5千米，求甲、乙两人的速度各是多少．21. 某中学要在全校学生中举办“中国梦⋅我的梦”主题演讲比赛，要求每班选一名代表参赛．九年级(1)班经过投票初选，小亮和小丽票数并列班级第一，现在他们都想代表本班参赛．经班长与他们协商决定，用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛)．规则如下：两人同时随机各掷一枚完全相同且质地均匀的骰子一次，向上一面的点数都是奇数，则小亮胜；向上一面的点数都是偶数，则小丽胜；否则，视为平局，若为平局，继续上述游戏，直至分出胜负为止．如果小亮和小丽按上述规则各掷一次骰子，那么请你解答下列问题：(1)小亮掷得向上一面的点数为奇数的概率是多少？(2)该游戏是否公平？请用列表或树状图等方法说明理由．(骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体)22. 某中学全校学生参加了“交通法规”知识竞赛，为了解全校学生竞赛成绩的情况，随机抽取了一部分学生的成绩，分成四组：A：60≤x<70；B：70≤x<80；C：80≤x<90；D：90≤x≤100．(1)请将条形统计图补充完整；(2)在扇形统计图中，计算出D：90≤x≤100这一组对应的圆心角是______度；(3)所抽取学生成绩的中位数在哪个组内，并说明理由；(4)若该学校有1500名学生，估计这次竞赛成绩在A：60≤x<70组的学生有多少人？23. 青龙寺是西安最著名的樱花观赏地，品种达到了13种之多，每年3、4月陆续开放的樱花让这里成为了花的海洋.一天，小明和小刚去青龙寺游玩，想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了，底部不易到达).小明在F处竖立了一根标杆EF，小刚走到C处时，站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离DC=1.6米；然后，小刚在C处蹲下，小明平移标杆到H处时，小刚恰好看到标杆顶端G和树的顶端B在一条直线上，此时测得小刚的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米，CF=2米，FH=1.6米，点C、F、H、A在一条直线上，点M在CD上，CD⊥AC，EF⊥AC，GH⊥AC，AB⊥AC.根据以上测量过程及测量数据，请你求出这棵樱花树AB的高度．24. 民族要复兴，乡村必振兴．2月21日发布的2021年中央一号文件，主题是全面推进乡村振兴，加快农业农村现代化．乡村振兴战略的实施效果要用农民生活富裕水平来评价，某合作社为尽快打开市场，对本地新产品进行线上和线下销售相结合的模式，具体费用标准如下：线下销售模式：标价5元/千克，八折出售；线上销售模式：标价5元/千克，九折出售，超过6千克时，超出部分每千克再让利1.5元．根据以上信息回答下列问题：(1)请分别求出两种销售模式下所需费用y(元)与购买产品数量x(千克)之间的函数关系式；(2)若想购买这种产品10千克，请问选择哪种销售模式购买最省钱？25. 如图，以△ABC的边AC为直径的⊙O恰好为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE//AC交BC的延长线于点E．(1)求证：DE是⊙O的切线；(2)若AB=8，tan∠BAC=1，求DE的长．226. 如图，抛物线与x轴交于点A(1,0)，B(3,0)，与y轴交于点C(0,3)．(1)求二次函数的表达式及顶点坐标；(2)连接BC，在抛物线的对称轴上是否存在一点E，使△BCE是直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由．27. 问题提出：(1)如图1，在正方形ABCD中，E为正方形CB边上一点，过AE的中点F作MNꓕAE交DC于M，交AB于N，则AE与MN的数量关系为______．问题探究：(2)如图2，在矩形ABCD中，AB=6，BC=8，E为CD边上的点，且CE=2，连接BE，过BE的中点F作MNꓕBE交AD于M，交CB于N，求BN的长度．问题解决：(3)如图3，在四边形ABCD中，AD//BC，∠D=90°，∠ABC=60°，AB=AD=8，E为CD边上一点，连接BE，过BE的中点F作MNꓕBE交CB于N，交AD于M，设CE的长为x，四边形AMNB 的面积为y，求y关于x的函数解析式，并说明当AE为何值时，四边形AMNB的面积最小，最小值是多少？答案和解析1.【答案】B【解析】解：(−2)0=1．故选：B．根据零指数幂：a0=1(a≠0)，进而得出答案．此题主要考查了零指数幂，正确掌握零指数幂的性质是解题关键．2.【答案】C【解析】解：综合主视图和俯视图，这个几何体的右边一列有2个正方体，左边一列最少有4个正方体，所以组成这个几何体的小正方块最少有6块．故选：C．根据三视图的知识，易得这个几何体共有3层，2行，2列，先看右边一列正方体的个数，再看左边一列正方体的可能的最少个数，相加即可．本题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就容易得到答案．3.【答案】A【解析】解：原式=1a−b−a(a+b)(a−b)=a+b(a+b)(a−b)−a(a+b)(a−b) =a+b−a(a+b)(a−b)=ba2−b2，故选：A．异分母分式相加减，先通分，化为同分母分式，再化简即可．本题考查了分式的加减法，对于分母是多项式的分式，首先考虑因式分解，这是解题的关键．4.【答案】C【解析】解：∵a//b，∴∠1=∠DBC=50°．∵∠DBC=∠A+∠2，∴∠A=∠DBC−∠2=50°−28°=22°．故选：C．根据三角形外角的性质，∠A=∠DBC−∠2，欲求∠A，需求∠DBC.根据平行线的性质，由a//b，得∠1=∠DBC=50°，从而解决此题．本题主要考查平行线的性质、三角形外角的性质，熟练掌握平行线的性质、三角形外角的性质是解决本题的关键．5.【答案】D【解析】解：∵直线y=(m−2)x+m+3经过一、二、四象限，∴{m−2<0m+3>0，解得−3<m<2，故选：D．根据一次函数y=kx+b中，图象经过一、二、四象限时，k与b的取值范围求解．本题考查一次函数图象的性质，解题关键是掌握y=kx+b中k与b的符号与图象的对应关系．6.【答案】A【解析】【分析】本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．根据三角形中位线定理得到EG=12AB，EG//AB，FG=12CD，FG//CD，根据平行线的性质求出∠EGD、∠DGF，进而求出∠EGF，再根据等腰三角形的性质、三角形内角和定理计算即可．【解答】解：∵E，G分别是AD，BD的中点，∴EG是△ADB的中位线，∴EG=12AB，EG//AB，∴∠EGD=∠ABD=20°，CD，FG//CD，同理可得：FG=12∴∠DGF=180°−∠BDC=110°，∴∠EGF=∠EGD+∠FGD=130°，∵AB=CD，∴EG=FG，×(180°−130°)=25°，∴∠GEF=12故选A．7.【答案】D，【解析】解：原抛物线开口向上，对称轴为：x=m+14，绕原点旋转180°后得到抛物线C′的开口向下，对称轴为：x=−m+14∵当x<1时，y随x的增大而增大，≥1，∴−m+14∴m≤−5．故选：D．先确定旋转后抛物线的开口和对称轴，再求m的范围．本题考查二次函数的图象和性质，确定旋转后抛物线的开口和对称轴是求解本题的关键．8.【答案】x>1【解析】解：移项，得：5x>3+2，合并同类项，得：5x>5，系数化为1，得：x>1，故答案为：x>1．移项、合并同类项、系数化为1即可．本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．9.【答案】4π【解析】解：∵扇形的弧长为2πcm ，半径为4cm ，∴该扇形的面积为12×2π×4=4π(cm 2)， 故答案为：4π．根据扇形的面积公式求出即可．本题考查了弧长的计算和扇形面积的计算，注意：已知扇形的圆心角是n°，半径是r ，那么这个圆心角所对的弧的长度是nπr 180，这个扇形的面积=nπr 2360=12×弧长×r ．10.【答案】72【解析】【分析】本题主要考查了正多边形和圆，多边形的内角和定理，等腰三角形的性质，熟练掌握多边形的内角和定理是解决问题的关键．由多边形的内角和与正多边形的定义求得∠CDE =∠E =108°，AE =DE ，由等腰三角形的性质求得∠EDA =36°，进而求得∠CDF =72°，再根据等腰三角形的性质即可求得∠CFD ．【解答】解：∵五边形ABCDE 是正五边形，∴∠CDE =∠E =(5−2)×180°5=108°，AE =DE ， ∴∠EDA =∠EAD =12(180°−∠E)=36°，∴∠CDF =∠CDE −∠EDA =108°−36°=72°，∵CF =CD ，∴∠CFD =∠CDF =72°，故答案为：72．11.【答案】2+√5【解析】解：∵C 、D 两点都是AB 的黄金分割点，∴AC =√5−12AB ，BD =√5−12AB ，∴AC +BD =(√5−1)AB ，即AB +CD =(√5−1)AB ，∴AB =√5+2，故答案为：√5+2．利用黄金分割的定义得到AC=√5−12AB，BD=√5−12AB，则AC+BD=(√5−1)AB，即可解决问题．本题考查了黄金分割：把线段AB分成两条线段AC和BC(AC>BC)，且使AC是AB和BC的比例中项(即AB：AC=AC：BC)，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AC=√5−12AB≈0.618AB，并且线段AB的黄金分割点有两个．12.【答案】569【解析】解：∵y=−12x+2，∴x=0时，y=2；y=0时，−12x+2=0，解得x=4，∴A(4,0)，B(0,2)．∵四边形ABCD是矩形，∴∠ABC=90°．设直线BC的解析式为y=2x+b，将B(0,2)代入得，b=2，∴直线BC的解析式为y=2x+2，设C(a,2a+2)，∵矩形ABCD的对称中心为点M，∴M为AC的中点，∴M(a+42,a+1)．∵双曲线y=kx(x>0)过点C、M，∴a(2a+2)=a+42(a+1)，解得a1=43，a2=−1(不合题意舍去)，∴k=a(2a+2)=43(2×43+2)=569．故答案为569．先由直线y=−12x+2与x，y轴交于A、B两点，求出A(4,0)，B(0,2)，根据互相垂直的两直线斜率之积为−1，求出直线BC的解析式为y=2x+2，设C(a,2a+2)，由矩形的对称中心为点M，得出M为AC的中点，根据中点坐标公式得出M(a+42,a+1)，再根据双曲线y=kx(x>0)过点C、M，得到a(2a+2)=a+42(a+1)，解方程求出a的值，进而得到k．本题考查了反比例函数、一次函数图象上点的坐标特征，矩形的性质，中点坐标公式，待定系数法求一次函数的解析式，难度适中．求出M点的坐标是解题的关键．13.【答案】4√10【解析】解：过点B作BD⊥AC于点D，∵∠C=45°，∴△BCD为等腰直角三角形，∴BD=CD，设BD=CD=a，延长AC至点F，使得CF=a，∵tan∠AFB=a2a =12，作△ABF的外接圆⊙O，过点O作OE⊥AB于点E，则AE=12AB=2，∠AOE=∠AFB，∴tan∠AOE=12，∴OE=4，OA=√22+42=2√5，∴√2AC+BC=√2(AC+√22BC)=√2(AC+CF)=√2AF≤√2(OA+OF)，∴√2AC+BC的最大值为√2×4√5=4√10．故答案为：4√10．过点B 作BD ⊥AC 于点D ，则△BCD 为等腰直角三角形，设BD =CD =a ，延长AC 至点F ，使得CF =a ，则可求出tan∠AFB ，作△ABF 的外接圆⊙O ，过点O 作OE ⊥AB 于点E ，则AE =12AB =2，∠AOE =∠AFB ，则可利用tan∠AOE 求出OE 、OA ，最后利用三角形三边关系即可求出√2AC +BC 的最大值为√2(OA +OF)，计算即可．本题是几何综合题，涉及到等腰直角三角形的性质、锐角三角函数、勾股定理、圆周角定理、垂径定理、三角形三边关系、定弦定角构造圆等，解题关键是构造辅助线将√22BC 转化．14.【答案】解：原式=9+1−2√2+2+2×√22=9+1−2√2+2+√2 =12−√2．【解析】根据负整数指数幂、零指数幂、绝对值和特殊角的函数值计算即可．本题考查实数的运算，熟练掌握负整数指数幂、零指数幂、绝对值和特殊角的函数值是解题关键．15.【答案】解：(a +1)(a −3)−(a −2)2．=a 2−2a −3−(a 2−4a +4) =2a −7．【解析】利用多项式乘以多项式运算法则以及完全平方公式展开，合并同类项得出即可． 此题主要考查了整式的混合运算，正确掌握乘法公式是解题关键．16.【答案】解：由(1)得：x +3=3y ，即x =3y −3.(3) 由(2)得：2x −y =4，(4) 把(3)代入(4)得：y =2， 把y =2代入(3)得：x =3． 因此原方程组的解为{x =3y =2．【解析】解此题采用代入消元法最简单，解题时注意要细心．此题考查了学生的计算能力，解题时要仔细审题，选择适宜的解题方法会达到事半功倍的效果．17.【答案】解：去分母得：x2+2x+1−x2+1=4，移项合并得：2x=2，解得：x=1，经检验x=1是增根，分式方程无解．【解析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．18.【答案】解：如图，MN为所作；由作法得MN为△ABC的中位线，∴MN//BC，MN=12BC，∴△AMN∽△ABC，∴S△AMN：S△ABC=(MNBC )2=14，即S△AMN=14S△ABC．【解析】本题考查了作图−复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了三角形中位线的性质和相似三角形的判定与性质．作AB和AC的垂直平分线得到MN为△ABC的中位线，利用MN//BC可判断△AMN∽△ABC，然后根据相似三角形的性质可得到S△AMN=14S△ABC．19.【答案】证明：∵MN是AC的垂直平分线，∴AO=CO，∠AOM=∠CON=90°，∵四边形ABCD是平行四边形，∴AB//CD，AB=CD，∴∠M=∠N，在△AOM和△CON中，{∠M=∠N∠AOM=∠CON AO=CO，∴△AOM≌△CON(AAS)，∴AM=CN，∵AB=CD，∴BM=DN．【解析】根据垂直平分线的性质和平行四边形的性质可以证明△AOM≌△CON，得AM=CN，进而可得结论．本题考查了平行四边形的性质，全等三角形的判定与性质，线段垂直平分线的性质，解决本题的关键是综合运用以上知识．20.【答案】解：设乙的速度为x千米/时，则甲的速度为5x千米/时，依题意得：94×(5x+x)=67.5×2，解得：x=10，∴5x=5×10=50．答：甲的速度为50千米/时，乙的速度为10千米/时．【解析】设乙的速度为x千米/时，则甲的速度为5x千米/时，利用甲、乙的速度之后×相遇时间=A，B两地间的路程的2倍，即可得出关于x的一元一次方程，解之即可得出乙的速度，再将其代入5x中即可求出甲的速度．本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．21.【答案】解：(1)∵向上一面的点数为奇数有3种情况，∴小亮掷得向上一面的点数为奇数的概率是：36=12．(2)填表如下：由上表可知，一共有36种等可能的结果，其中小亮、小丽获胜各有9种结果．∴P(小亮胜)=936=14，P(小丽胜)=936=14，∴游戏是公平的．【解析】(1)首先判断出向上一面的点数为奇数有3种情况，然后根据概率公式，求出小亮掷得向上一面的点数为奇数的概率是多少即可．(2)首先应用列表法，列举出所有可能的结果，然后分别判断出小亮、小丽获胜的概率是多少，再比较它们的大小，判断出该游戏是否公平即可．(1)此题主要考查了判断游戏公平性问题，要熟练掌握，首先计算每个事件的概率，然后比较概率的大小，概率相等就公平，否则就不公平．(2)此题主要考查了列举法(树形图法)求概率问题，解答此类问题的关键在于列举出所有可能的结果，列表法是一种，但当一个事件涉及三个或更多元素时，为不重不漏地列出所有可能的结果，通常采用树形图．22.【答案】108【解析】解：(1)本次抽取的学生有：12÷20%=60(人)，C组学生有：60−6−12−18=24(人)，补全条形统计图如下：(2)90≤x≤100这一组对应的圆心角是360°×18=108°，60故答案为：108；(3)∵一共有60个数据，其中位数是第30、31个数据的平均数，而第30、31个数据均落在C组，∴所抽取学生成绩的中位数落在C：80≤x<90这一组内；(4)1500×6=150(人)，60答：这次竞赛成绩在A：60≤x<70组的学生有150人．(1)根据B组人数和所占的百分比，可以求得本次调查的人数，再根据条形统计图中的数据，即可得到C组的人数；(2)用360°乘以D组人数所占比例即可；(3)根据条形统计图中的数据，可以得到所抽取学生成绩的中位数落在哪个组内；(4)根据条形统计图中的数据，可以计算出这次竞赛成绩在A：60≤x<70组的学生有多少人．此题主要考查读频数分布直方图的能力和利用统计图获取信息的能力．解题的关键是根据直方图得到进一步解题的有关信息．23.【答案】解：过点D作DP⊥AB于点P，交EF于点N，过点M作MQ⊥AB于点Q，交GH于点K，由题意可得：DP=MQ=AC，DN=CF=2米，MK=CH，AP=DC=1.6米，AQ=HK=MC=0.8米．∵∠EDN=∠BDP，∠END=∠BPD=90°，∠GMK=∠BMQ，∠GKM=BQM=90°，∴△DEN∽△DBP ，△GMK∽△BMQ ， ∴BPEN =DPDN ，BQGK =QMMK ． ∴AB−1.62.4−1.6=AC 2，AB−0.82.4−0.8=AC2+1.6． ∴AB =8.8(米)．答：这棵樱花树AB 的高度是8.8米．【解析】过点D 作DP ⊥AB 于点P ，交EF 于点N ，过点M 作MQ ⊥AB 于点Q ，交GH 于点K ，构造相似三角形：△DEN∽△DBP ，△GMK∽△BMQ ，利用相似三角形的对应边成比例求得相关线段的长度即可．本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．24.【答案】解：(1)由题意知，线下销售：y =5×0.8x =4x ；线上销售：当0≤x ≤6时，y =5×0.9x =4.5x ；当x >6时，y =5×0.9×6+(x −6)×(5×0.9−1.5)=27+3(x −6)=3x +9， ∴y ={4.5x(0≤x ≤6)3x +9(x >6)，∴线下销售y 与x 之间的函数关系为y =4x ，线上销售y 与x 之间的函数关系为y ={4.5x(0≤x ≤6)3x +9(x >6)；(2)当x =10时，线下需花费：y =4x =4×10=40， 线上需花费：y =3x +9=3×10+9=39， ∵40>39，∴购买这种产品10千克，线上购买最省钱．【解析】本题考查一次函数的应用，解答本题的关键是明确题意，写出相应的函数解析式． (1)根据题意和题目中的数据，可以分别写出两种销售模式下所需费用y(元)与购买产品数量x(千克)之间的函数关系式；(2)将x =10代入(1)中的函数解析式，求出相应的函数值，然后比较大小，即可得到选择哪种销售模式购买最省钱．25.【答案】(1)证明：连接OD，∵AC是⊙O的直径，∴∠ABC=90°，∵BD平分∠ABC，∴∠ABD=1∠ABC=45°，2∴∠AOD=2∠ABD=90°，∵AC//DE，∴∠AOD=∠ODE=90°，∵OD是⊙O的半径，∴DE是⊙O的切线；(2)过点C作CG⊥DE，垂足为G，∴∠CGD=∠CGE=90°，∵∠AOD=90°，∴∠DOC=180°−∠AOD=90°，∴四边形ODGC是矩形，∵OD=OC，∴四边形ODGC是正方形，∴CG=DG=OD=OC，∵∠ABC=90°，AB=8，tan∠BAC=12，∴BC=ABtan∠BAC=8×12=4，∴AC=√AB2+BC2=√82+42=4√5，∴CG=DG=OD=OC=2√5，∵AC//DE，∴∠ACB=∠E，∴tan∠ACB=tan∠E，∴AB BC =CGGE，8 4=2√5GE，∴GE=√5，∴DE=DG+GE=3√5，∴DE的长为3√5．【解析】(1)连接OD，根据直径所对的圆周角是直角可得∠ABC=90°，再利用角平分线的定义可得∠ABD=45°，从而求出∠AOD，最后利用平行线的性质，求出∠ODE即可解答；(2)过点C作CG⊥DE，垂足为G，从而可证明四边形ODGC是正方形，可得CG=DG=OD=OC，然后在Rt△ABC中求出BC，AC，再根据平行线的性质可得∠ACB=∠E，最后再利用三角函数进行计算即可解答．本题考查了切线的判定与性质，解直角三角形，圆周角定理，三角形的外接圆与外心，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.【答案】解：(1)设抛物线的解析式为y=a(x−1)(x−3)，将点C(0,3)代入y=a(x−1)(x−3)，∴3a=3，∴a=1，∴y=(x−1)(x−3)=x2−4x+3，∵y=x2−4x+3=(x−2)2−1，∴顶点为(2,−1)；(2)存在一点E，使△BCE是直角三角形，理由如下：∵y=x2−4x+3=(x−2)2−1，∴抛物线的对称轴为直线x=2，设E(2,t)，∵△BCE是直角三角形，∴BE⊥CE，∵B(3,0)，C(0,3)，∴BC=3√2，BE=√1+t2，CE=√4+(t−3)2，①当BC为斜边时，∴18=(√1+t2)2+(√4+(t−3)2)2，解得t=3±√172，∴E点坐标为(2,3+√172)或(2,3−√172)；②当BE为斜边时，∴18+(√4+(t−3)2)2=(√1+t2)2，解得t=7，∴E点坐标为(2,7)；③当CE为斜边时，∴18+(√1+t2)2=(√4+(t−3)2)2，解得t=1，∴E点坐标为(2,1)；综上所述：E点坐标为(2,3+√172)或(2,3−√172)或(2,7)或(2,1)．【解析】(1)设抛物线的解析式为y=a(x−1)(x−3)，将点C(0,3)代入即可求解；(2)设E(2,t)，则BC=3√2，BE=√1+t2，CE=√4+(t−3)2，分三种情况讨论，①当BC为斜边时；②当BE为斜边时；③当CE为斜边时；利用勾股定理分别求出t的值，即可求E点坐标．本题考查二次函数的综合应用，熟练掌握二次函数的图象及性质，直角三角形的勾股定理是解题的关键．27.【答案】AE=MN【解析】(1)解：AE=MN，过点M作MG⊥AB于G，交AE于点H，∴∠MGN=90°，∵MN⊥AE，∴∠MFH=90°，∵∠HMF+∠MHF=90°，∠HAG+∠AHG=90°，∠AHG=∠MHF，∴∠HAG=∠HMF，在△MGN和△ABE中，{∠GMN=∠BAE MG=AB∠MGN=∠ABE，∴△MGN≌△ABE(ASA)，∴AE=MN，故答案为：AE=MN；(2)解：连接EN，∵点F是线段BE的中点，MN⊥BE，∴MN是BE的垂直平分线，∴BN=EN，设BN=EN=a，则CN=8−a，在Rt△CEN中，由勾股定理得，EN2=CN2+CE2，即a2=(8−a)2+22，解得：a=154，∴BN=154；(3)解：连接AE，过点A作AR⊥BC于R，过点F作PQ⊥AD于P，交BC于点Q，∴PQ//CD，∴四边形CDPQ是矩形，∵∠ABC=60°，∴BR=cos∠ABC⋅AB=12×8=4，AR=sin∠ABC⋅AB=√32×8=4√3，∴BC=BR+CR=4+8=12，∵PQ//CD，且点F是BE的中点，∴点Q是BC的中点，∴BQ=CQ=PD=6，∴FQ=12CE=12x，∵∠CBE=∠QBF，∠BCE=∠BQF，∴△BCE∽△BQF，∴∠BNF=∠BEC，∵∠FQN=∠BCE=90°，∴△BCE∽△FQN，∴BC CE =FQQN，即12x=2QN，∴QN=x224，∵BN=BQ+QN，∴BN=6+x224，∵PF=PQ−FQ，∴PF =4√3−x 2， ∵AD//BC ，∴∠PMF =∠BNF ，∵∠FBN +∠BNF =90°，∠FBN +∠BEC =90°，∴∠BNF =∠BEC ，∴∠FMP =∠BEC ，∵∠MPF =∠BCE =90°，∴△FPM∽△BCE ，∴FP PM =BC CE ，∴4√3−x 2PM =12x ，∴PM =√33x −x 224， ∵AP =AD −PD ，∴AP =8−6=2，∴AM =AP −PM=2−(√33x −x 224) =x 224−√33x +2，∴y =S 四边形AMNB =CD⋅(AM+BN)2=(x 224−√33x+2+6+x 224)×4√32=√36x 2−2x +16√3=√36(x −2√3)2+14√3，当x =2√3时，y 有最小值为14√3，∵DE =CD −CE ，∴DE =4√3−x=4√3−2√3=2√3，此时AE =√AD 2+DE 2=√82+(2√3)2=2√19，∴y 与x 的函数关系式为：y =√36x 2−2x +16√3，AE 为2√19时，四边形AMNB 面积最小为14√3． (1)过点M 作MG ⊥AB 于G ，根据ASA 证明△MGN 与△ABE 全等，进而利用全等三角形的性质解答即可；(2)连接EN，应用勾股定理求解即可；(3)连接AE，过点A作AR⊥BC于R，过点F作PQ⊥AD于P，Q，得出点Q是BC的中点，再证明△BCE∽△BQF和△FPM∽△BCE，根据梯形面积公式即可得出关系式，再利用二次函数性质即可求解．此题考查四边形综合题，涉及到三角形全等，四边形的性质，相似三角形的判定和性质以及勾股定理和二次函数性质等，掌握正方形和矩形以及梯形的性质是解题关键．。