5传递函数典型环节
- 格式:ppt
- 大小:1.43 MB
- 文档页数:24


1、反馈:输出信号被测量环节引回到输入端参与控制的作用。
2、开环控制系统与闭环控制系统的根本区别:有无反馈。
3、线性及非线性系统的定义及根本区别:当系统的数学模型能用线性微分方程描述时,该系统的称为线性系统。
非线性系统:一个系统,如果其输出不与其输入成正比,则它是非线性的。
根本区别:线性系统遵从叠加原理,而非线性系统不然。
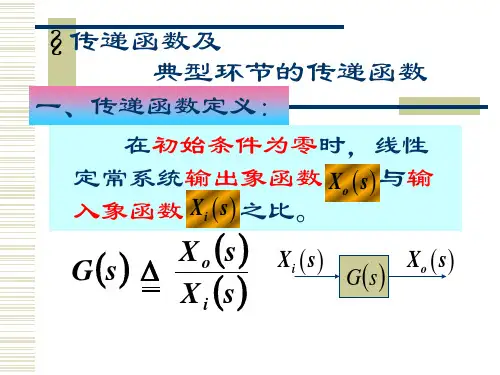
4、传递函数的定义及特点:零初始条件下,系统输出量的拉斯变换与输入量的拉斯变换的比值。
用G〔s〕表示。
特点:1〕、传递函数是否有量纲取决于输入与输出的性质,同性质无量纲。
2〕、传递函数分母中S的阶数必n不小于分子中的S的阶数m,既n=>m ,因为系统具有惯性。
3〕、假设输入已给定,则系统的输出完全取决于其传递函数。
4〕、物理量性质不同的系统,环节和元件可以具有相同类型的传递函数。
5〕、传递函数的分母与分子分别反映系统本身与外界无关的固有特性和系统同外界的关系。
5、开环函数的定义:前向通道传递函数G〔s〕与反馈回路传递函数H(s)之积。
6、时间响应的定义和组成:系统在激励信号作用下,输出随时间的变化关系。
按振动来源分为:零状态响应和零输入响应。
按振动性质:自由响应和强迫响应。
7、瞬态性能指标以及反映系统什么特性:性能指标:上升时间tr、峰值时间tp、最大超调量Mp、调整时间ts、振荡次数N。
这些性能指标主要反映系统对输入的响应的快速性。
8、稳态误差的定义及计算公式:系统进入稳态后的误差。
稳态误差反映稳态响应偏离系统希望值的程度。
衡量控制精度的程度。
稳态误差不仅取决于系统自身结构参数,而且与输入信号有关。
系统误差:输入信号与反馈信号之差。
9、减少输入引起稳态误差的措施:增大干扰作用点之前的回路的放大倍数K1,以及增加这一段回路中积分环节的数目。
10、频率响应的概念:线性定常系统对谐波输入的稳态响应称为频率响应。
11、频率特性的组成:幅频特性和相频特性。
12、稳定性的概念:系统在扰动作用下,输出偏离原平衡状态,待扰动消除后,系统能回到原平衡状态〔无静差系统〕或到达新的平衡状态〔有静差系统〕。



典型环节及其传递函数1.比例环节(放大环节)运动方程:,传递函数为:)t (Kr )t (c K )s (G,比例环节的典型例子有运算放大器、齿轮变速箱、电位器、测速发电机等。
2.惯性环节运动方程:)()()(t r t c dtt dc T+,传递函数:0011)(ωω++s Ts s G ,T 10ωT 称为惯性时间常数,只有一个实数极点T 1−,没有零点。
若输入为阶跃函数)()(t ul t r ,则该惯性环节的输出为:()[(0)]t T c t u c u e −=+−,为的初值。
)0(c c 典型的实例有一阶RC 电路。
3.积分环节运动方程:)()(t r dtt dc T 或∫t dt t r T t c 0)(1)(,即环节输出为输入信号的积分,环节由此得名。
传递函数:ss G 1)(积分环节的特点是除非输入信号恒为0,否则积分环节的输出量不可能维持为常数不变。
)(t r )(t c 4.微分环节运动方程:dtt dr Tt c )()(,即环节输出量为输入信号的微分,环节由此得名。
传递函数:,有时Ts s G )(1)(+Ts s G 也称为微分环节。
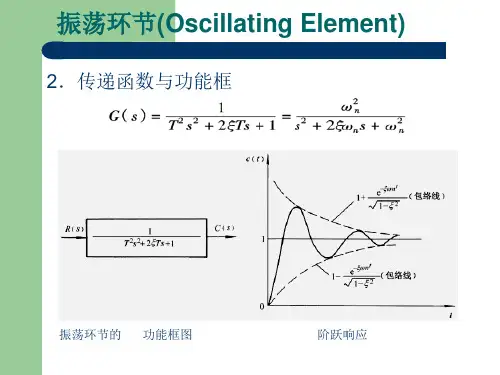
5.振荡环节运动方程:)()()(2)(222t r t c dt t dc T dtt c d T ++ξ传递函数:222222222121121)(nn n s s T T s s T Ts s T s G ωξωωξξ++++++其中T n 1ω,10<≤ξ。
该环节具有一对共轭复数极点,无零点。
其单位阶跃响应呈典型的振荡衰减形式。
6.延时环节运动方程:)()(τ−t r t c ,这个方程实际上不是微分方程而是差分方程。
传递函数:,是的无理函数,函数在s e s G τ−)(s s e τ−∞s 点有无穷多个极点和零点。
====================微分环节不能单独存在只能与其它环节配合使用,。



