典型环节及其传递函数

θ 1 θ 2
u(t ) K1[1 (t ) 2 (t )] K1 (t )
K1 2 K11 图2-9 电位器
U(t)
K1是单个电位器的传递函数， (t ) 1 (t ) 2 (t ) 是两个电位器电刷角位移之差，称误差角。
U (s) K1 ( s )
5 振荡环节
n 1 G( s) 2 2 2 2 T S 2TS 1 S 2 n S n
2
T
1
式中 ξ－阻尼比 , (0 1) n -自然振荡角频率（无阻尼振荡角频率）
n
振荡环节的单位阶跃响应曲线
特点：环节中有两个独立的储能元件，并可进行能量交换，其
电位器的负载效应一般要求rl17测速发电机测量角速度并将它转换成电压量的装置直流测速发电机交流测速发电机dt图210测速发电机转子角速度radsktktsk18电枢控制直流伺服电动机例29中求得电枢控制直流电动机简化后的微分方程为tmk2tmk1tmk1stm图212两相伺服电动机两相定子线圈和一个高电阻值的转子组成
（b)
(t ) 转子角速度（rad/s）
Kt
Ω (s)
H (s)
Kt SKt 图2-11
U(s)
输出斜率（v/rad/s）
U ( s) Kt S ( s)
U(s)
G( s)
G( s)
U ( s) Kt ( )
18
电枢控制直流伺服电动机 例2-9中求得电枢控制直流电动机简化后的微分方程为
G (s) C (s) R( s)
如果将
S
d dt
置换 传递函数 微分方程
8
性质7
传递函数G(s)的拉氏反变换是脉冲响应g(t) 脉冲响应（脉冲过渡函数）g(t)是系统在单位脉冲输 入时的输出响应。

1 xo t xi t dt T
•传递函数为：
1 G s X i s Ts
Xo s
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比，称为微分环节， 又称为理想微分环节 •动力学方程为：
xo t T
•传递函数为：
dxi t dt
典型环节的传递函数
8、延时环节 延时环节是输出滞后输入时间 但不失真地反映 输入的环节，又称为时滞环节。 •动力学方程为：

xo t xi t s Xi s
e s
•拉普拉斯变换：
F s L f t f t e dt 0
Ts
G s
Xo s Xi s
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节，是一个相位滞后环节。 •动力学方程为：
T
dxo t dt
xo t xi t
Xo s
•传递函数为：
1 G s X i s Ts 1
典型环节的传递函数
1、比例环节 凡输出量与输入量成正比，输出不失真也不延迟 而按比例地反映输入的环节，称为比例环节又叫 放大环节、无惯性环节、零阶环节 •动力学方程为：
xo t Kxi t
•传递函数为：
G s
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比，称为积分环节， 又称为理想积分环节 •动力学方程为：
st

s a i
•拉普拉斯反变换：
1 a i st f t L F s 2 i a i F s e ds

f (t) k
m
Bx 图2-1 机械移动系统
R
L
i(t)
ui (t)
C uo (t)
图2-3 RLC电路
由式 2-2 已知机械移动系统的微分方程为
m d 2 x B dx kx f t
dt 2
dt
通过拉氏变换求的其传递函数为
f (t) k
Gs X s
1
F s ms2 Bs k
=1
2 n
k s2 2 ns
Gs
KTD s
TD s 1
例图 为无源微分
C
电路，设电压ui t 为 输入量，电阻R两端电 ui (t)
R
uo (t)
压u0 t 为输出量。
其运动方程为： ui t Ri t u0 t Ri t
消去中间变量后，得：
ui t u0 t
其传递函数为：G s U0 s
Ui s
式中
TD RC
1i t dt C
2 n
m
Bx
式中 n
k; m
B。 2 km
由式 2-6 已知RLC电路的微分方程式为
LC d 2u0 t dt 2
RC du0 t dt
u0 t
ui t
通过拉氏变换求得其传递函数为
G s U0 s
1
Ui s LCs2 RCs 1
2
= s2
n
2 ns
2 n
R
L
式中
n
1; LC
R 。 ui(t) 2 L/C
钢板厚度偏差 2 t 与A点
处的厚度偏差 其传递函数为
1 t 之间有如下关系
2t=
t-
1
G s =e- s

02
传递函数的零点和极点决定了系统的动态特性和稳定性。
03
传递函数的分子和分母多项式决定了系统的频率响应特性。
典型环节的分类
比例环节
输出信号与输入信号成正比，传递函 数为 G(s) = K，其中 K 为常数。
02
积分环节
输出信号与输入信号的时间积分成正 比，传递函数为 G(s) = 1 / (sT)，其 中 T 为时间常数。
将介绍控制系统的稳定性 分析方法。
掌握频率响应法在控制系 统设计中的应用。
学习如何利用根轨迹法进 行系统性能分析。
了解现代控制系统的基本 概念和分类。
THANKS FOR WATCHING
感谢您的观看
高阶环节的传递函数具有多个极点和零点，这些极点和零点 决定了环节的动态特性，如响应速度、超调和调节时间等。
实例分析
以一个三阶惯性环节为例，其传递函数为 $G(s) = frac{1}{s^3 + 2s^2 + 3s + 1}$，该环节具有三个极点 $s = -1, -1, -1$ 和一个 零点 $s = 0$。
拉普拉斯变换中的频率。
该传递函数是一个有理分式，分 母为线性多项式，分子为常数。
当输入信号 (s) 变化时，输出信 号 (G(s)) 会根据增益 (K) 和时间
常数 (T) 进行相应的变化。
实例分析
实例1
一阶惯性环节在电机控制系统中的应用，用于描述电机的动态响应特性。
实例2
在温度控制系统中的一阶惯性环节，用于描述加热元件的热量传递和散热过程。
04 一阶惯环节
定义与特点
定义
一阶惯性环节的传递函数为 (G(s) = frac{K}{T s + 1})，其中 (K) 是增益，(T) 是时间常 数。

则G(s) = Uo s = RCS
(RC = T
K 1
Ui s RCS + 1
K = 1)
Gs k
4 积分环节
s
时间域方程
xo t k xi t dt
X o s
k
X i s
s
X o s X i s
k s
例9
i2(t)
i1(t) ui(t)
R
A
B
C
_
K0 +
uo(t)
ui (t) = -C duo (t)
传递函数及 典型环节的传递函数
一、传递函数定义：
在初始条件为零时，线性
定常系统输出象函数 Xo s与输 入象函数 Xi s 之比。
Gs
X o s Xi s
Xi s Gs Xo s
设线性定常系统的微分方程为：
a
0
xon
t
a1
x
n1
o
t
a
n1
x
o
t
a
n
x
o
t
b0
x
m
i
t
b1
x
m
i
1
t
bm 1
x i
t
则G(s) = Uo s =
1
Ui s RCS + 1
(RC = T)
例4
弹簧-阻尼系统
K
xi
t
xo
t
D
dxo
dt
t
KXi s KXo s DsXo s
Gs
Xo s Xi s
K Ds
K
D
1 s 1
K
Gs Ks

c（t）（= T1）￲或r （t）dt
T
dc（t） dt
=
r
t
式中：T 为积分时间常数。 （ 2） 传 递 函 数
G（s）
=
C（s） R（s）
=
1 Ts
（ 3） 特 点 积分环节中输出量为输入量对时间的积累。若输入突变，输出值要经一段时间积累后才
等于输入值，故有滞后作用。即便是输入变为零，输出也保持原值不变，即具有记忆功能。 只有当输入反向时，输出才反向积分而下降。
典型环节有：比例环节、积分环节、理想积分环节、惯性环节、比例微分环节、振荡环节和 延时环节等。 1.比 例 环 节 比例环节又称放大环节，其输出量变化与输入量变化成比例关系，也就是说，它的输出量 能够按照一定的比例复现输入量。 （ 1） 微 分 方 程
c（t）（= K）r t
（ 2） 传 递 函 数
7.延迟环节
（1）微分方程
c（） t （ = ）r t-τ 0
式中：r0为延时时间。 （2）传递函数
G（s） = e-t02
（3）特点
延迟环节的输出波形与输入波形相同，但延迟了时间。延迟环节的存在对系统的稳 定性不利。
例：求运算放大器构成的惯性环节的传递函数
R2
解： G(s)
=
Uo（s） Ui（s）
=
-
R1 R2Cs
+1
4理 想 微 分 环 节 传递函数为：
G(s)= CR((ss)) =Tc s
4.理想微分环节 理想微分环节是积分环节逆运算，其输出量反映了输入信号的变化趋势。
（1）微分方程
c（t）
=ቤተ መጻሕፍቲ ባይዱ
t
dr（t） dt
式中：r为微分时间常数。

1
气阻的数学表达式为 ∆p = R∆q ∆p 式中， 是气体压力降 ； ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ； R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) （３）喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 １，背压室 ２，喷嘴 ３，和挡板 ４ 组成，如图 ２－１８ 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时，可把喷嘴 1 2 4 一挡板机构看作一个比例环节，即 3 D ∆p D = k 1 ∆h 式中， 是喷嘴背压的变化； ∆p D ∆h 是挡板开度变化量； 是比例系数。 k1 d （４）放大器 h 在自动控制系统中用得最多的是运算放大 器，它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成，其符号如图 ２－ 3 − 喷嘴 4 − 挡板 １９ 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端，输出电压为 u 0 (t ) 它有两个输入端，一个是同相输入端 ｂ 用 “十”表示，一个是反相输入端 ａ 用“一”表示。当 放大器工作在放大区而不是饱和区时，输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中， 为开环放大倍数，这个数值很高，可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点： ①由于开环输入电阻很高，运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高，所以 ｂ 端和 Ｃ 端电位接近相等，即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节，但可用它来组成其他各种基本环节。

hc t hd (t )
l
v
2.3 控制系统的复数域数学模型
4.典型元部件的传递函数
（1）电位计
（1）比例环节
（2）电桥式误差角检测器
（2）微分环节
（3）自整角机
（3）积分环节
（4）测速发电机（交流，直流） （4）惯性环节
（5）电枢控制式直流电动机 （5）振荡环节
（6）两相异步电动机
（6）一阶复合微分环节
特点： 输出量能准确复现输入量，但须延迟一固定的时 间间隔。
在线性控制系统中，系统含有典型环节的情况，反映了系 统的结构和性能。
时滞环节
对于时滞时间很小的时滞环节，常把它展开成泰勒级数，并 略去高次项，得：
W
(
s)
1
s
2
s
2
1
3
s3
2! 3!
1
1s
时滞环节在一定条件下可近似为惯性环节
实例
带钢厚度检测环节
(6)
复习拉普拉斯变换有关内容（13）
用L变换方法解线性常微分方程
0 初条件 n>m
: 特征根（极点） : 相对于 的模态
2.3 控制系统的复数域数学模型
3.传递函数的零点和极点对输出的影响
极点决定模态； 零点影响曲线形状。
4 传递函数的局限性
例 已知某系统在0初条件下的阶跃响应为：
c(t) 1 2 et 1 e4t 33
试求：（1） 系统的传递函数； （2） 系统的增益； （3） 系统的特征根； （4） 画出对应的零极点图； （5） 求系统的单位脉冲响应； （6） 求系统微分方程；
解.（1）
(2) (3) (4) 如图所示 (5)
积分环节实例：

典型环节的传递函数
1、比例环节 凡输出量与输入量成正比，输出不失真也不延迟 而按比例地反映输入的环节，称为比例环节又叫 放大环节、无惯性环节、零阶环节
•动力学方程为：
xotKxit
•传递函数为：
Gs
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比，称为积分环节， 又称为理想积分环节
•动力学方程为：
Tdxdottxotxit
•传递函数为：
GsXXoi ss
1 Ts1
典型环节的传递函数
5、导前环节(一阶微分环节) 又称为一阶微分环节，是一个相位超前环节。
•传递函数为：
GsXXoi ssTs1
典型环节的传递函数
6、振荡环节(二பைடு நூலகம்积分环节) 振荡环节是二阶环节，又称二阶振荡环节
•传递函数为：
•动力学方程为：
xotT1xi tdt
•传递函数为：
Gs
Xo s Xi s
1 Ts
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比，称为微分环节， 又称为理想微分环节
•动力学方程为：
xo
t
T
dxi t
dt
•传递函数为：
Gs
Xo s Xi s
Ts
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节，是一个相位滞后环节。
G sX Xo isss22 n 2 nsn 2
GsX Xo issT2s22 1Ts1
典型环节的传递函数
7、二阶微分环节
•传递函数为：
G sX Xo isss22 n 2 nsn 2 GsX Xo issT2s22Ts1

21
一、典型输入信号
1. 阶跃函数：
r(t)
a t 0
a
r(t) 0 t 0
t
单位阶跃函数：
1 t 0 r(t) 1(t) 0 t 0
单位阶跃函数的拉氏变换
R(s) L[1(t)] 1 s
22
2. 速度函数(斜坡函数)：
r(t)
at t 0
r(t)
0
t0
at
t
单位速度函数(斜坡函数)：
传递函数为： G(s)
1
s
积分环节原理图为：
U2(s) 1/ Cf s 1 1 U1(s) R1 R1C f s Tis
4
空载油缸
流量：
Q
f
(t)
A
dx(t) dt
X (s) 1/ A K Q f (s) s s
小惯性电动机
m(s) Km
Ua(s) s
三、理想微分环节 微分方程为：c(t) dr(t)
4. 调节时间ts:整个过渡过程所经历的时间，有时也叫过渡过 程时间。
30
5. 超调量σ%: 响应过程中，输出量
超出稳态值的最大偏差值， 一般用它与稳态值的比值 的百分数表示，即
% h(t p ) h() 100%
h()
6. 振荡次数N:单位阶跃响应曲线在0→ts时间内，穿越稳态 值次数的一半称为振荡次数。
31
7.稳态误差ess:对单位 负反馈系统，当时间t 趋于无穷时，系统单 位阶跃响应的期望值 [即输入量1(t)] 与实际值 (即稳态值)之差，定义为 稳态误差:
ess =1 - h(∞)
当h(∞) =1时，系统的稳态误差为零。
32
注意： σ%

典型环节及传递函数
惯性环节实例
G(s)= 1 = 1 ，T=RC RCs+1 Ts+1
R
+
+
i
ur
C uc
-
-
典型环节及传递函数
3、积分环节
1 微分方程: c t = T න r t dt
传递函数:
G(s)=
C(s)= R(s)
1 Ts
方框图: R(s)
1
C(s)
Ts
特点：输出量与输入量对时间的积分成正比，具有滞后作 用和记忆功能.
典型环节及传递函数
实例：
ur (t)
R1
R2 uc (t)
其中，比例系数 K= R2 R 1+R 2
典型环节及传递函数
例1 如图a所示的电压分压器即为一典型比例环节， 当输入量r(t)为阶跃变化信号时，输出量y(t)的 变化如图b所示
典型环节及传递函数
2、惯性环节
微分方程: T dc(t)+c(t)=r(t) dt
c(t)=1-e-
t T
典型环节及传递函数
单位阶跃信号作用下的响应:
1.0 r(t)
0.8
c(t)
0.95 0.98 0.99
0.6
0.87
0.4
0.63
0.2
T 2T 3T 4T 5T t
在单位阶跃输入信号的作用下，惯性环节的输出信号是指 数函数。当时间t=(3~4)T时，输出量才接近其稳态值。
G(s)=
Y(s) F(s)
=
1 ms2+fs+k
特点： 1、含有两种形式的储能元件，并能将储存的能量相互转
换。如动能与位能、电能与磁能间转换。

Uo ( s ) R2 G( s ) K Ui ( s ) R1
第二章 控制系统的数学模型
§2-3 传递函数及基本环节的传递函数
惯性环节
凡运动方程为一阶微分方程：
d T xo ( t ) xo ( t ) Kxi ( t ) dt
形式的环节称为惯性环节。其传递函数为：
Xo( s ) K G( s ) X i ( s ) Ts 1
运动方程为：
式中，T—微分环节的时间常数
在物理系统中微分环节不独立存在，而是和 其它环节一起出现。
第二章 控制系统的数学模型
§2-3 传递函数及基本环节的传递函数
无源微分网络
1 ui ( t ) i ( t )dt i ( t )R C uo ( t ) i ( t )R
RCs Ts G( s ) , T RC RCs 1 Ts 1
G( s ) K 1 C , T Cs K Ts 1 K
第二章 控制系统的数学模型
§2-3 传递函数及基本环节的传递函数
微分环节 输出量正比于输入量的微分。
dx i (t ) x o (t ) T dt X o ( s) 传递函数为： G ( s) Ts X i ( s)

t
0
xi ( t )dt
传递函数为： G( s )
Xo( s ) 1 X i ( s ) Ts
式中，T—积分环节的时间常数。
第二章 控制系统的数学模型
§2-3 传递函数及基本环节的传递函数
积分环节特点：
.输出累加特性； .输出的滞后作用； .记忆功能。
如当输入量为常值 A 时，由于：
1 t 1 xo (t ) 0 Adt At T T

sX o (s)
+
k A2 R
X o (s)
=
sX i (s)
得到传递函数
G(s) = X o (s) = s = Ts
Xi (s)
s
+
k A2R
Ts +1
T = A2R k
由上面传递函数形式看出，液压阻尼器是包含有惯性环 节和微分环节的系统，称之为具有惯性的微分环节。
若|Ts|<<1时，G(s)≈Ts，系统近似成为理想微分环节。
如果对微分方程进行拉氏变换，得到代数方程(复数域)， 将使解算简化而方便。传递函数是在拉普拉斯变换基础上产生 的，可以用来方便直观地描述零初始条件下的单输入单输出系 统，是对元件及系统进行分析、研究与综合的有力工具。
根据传递函数在复平面上的形状可以直接判断系统的动态 性能，找出改善系统品质的方法。传递函数是经典控制理论的 基础，是极其重要的基本概念。
得到系统（或环节）传递函数的一般形式
G(s) =
X o (s) Xi (s)
=
bmsm + bm−1sm−1 + L+ b1s + b0 ansn + an−1sn−1 + L+ a1s + a0
由此可知，只要知道系统微分方程，就可求出其传递函
数。
上海大学 机电工程与自动化学院
2.3 传递函数
2.3.3 传递函数的特点
微分环节的方框图
因此，理想微分环节的传递函数为
微分环节的 时间常数
G(s) = X o (s) = Ts
Xi(s)
Ts
Xo(s)
Xi (s)
当输入量为阶跃函数时，理论上输出量将是一个幅值为

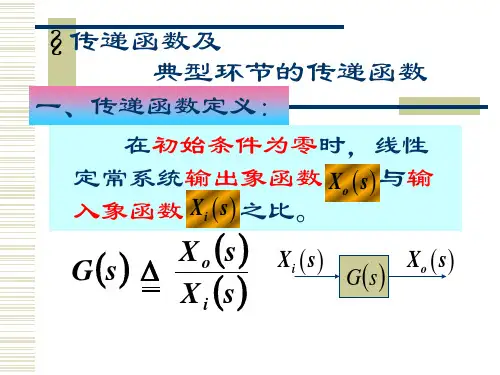
典型函数的传递函数是指描述系统输入与输出之间关系的函数。

在控制系统中，传递函数通常用于描述线性时不变系统的动态行为。

传递函数可以是连续时间的，也可以是离散时间的。

传递函数的一般形式为：G(s) = Y(s)/X(s)，其中G(s)是传递函数，Y(s)是输出信号的拉普拉斯变换，X(s)是输入信号的拉普拉斯变换。

传递函数描述了系统对输入信号的响应方式。

对于典型函数，其传递函数的形式会根据具体的系统类型和结构而有所不同。

以下是一些常见的典型函数及其传递函数的示例：
1. 比例环节（Proportional element）：传递函数为K，其中K 是比例系数。

输出与输入成正比关系。

2. 积分环节（Integral element）：传递函数为1/s，其中s 是复变量。

输出是输入的积分。

3. 微分环节（Derivative element）：传递函数为s，输出是输入的微分。

4. 一阶惯性环节（First-order inertial element）：传递函数为K/(Ts+1)，其中T 是时间常数。

该环节具有一阶滞后特性。

5. 二阶振荡环节（Second-order oscillating element）：传递函数为K/(s^2+2ζωs+ω^2)，其中ζ是阻尼比，ω是自然频率。

该环节具有二阶振荡特性。

以上仅是一些常见的典型函数及其传递函数的示例，实际上还有很多其他类型的典型函数和传递函数形式。

在实际应用中，根据具体的系统要求和特点选择合适的典型函数和传递函数进行建模和分析。

j
j 1
0j 1
Im
0
Re
0
积分与微分环节
L(dB) 40
积分环节
0
微分环节
40
( )
90
微分环节
0 90
积分环节
20dB / dec
20dB / dec
6
三、微分环节
传递函数: G s s
频率特性:
G(j)
j
ej
π 2
➢1. 幅频特性 A及相频特性
A ,
A
( )
0
1
T
4
2
L,
0
1
T 3dB
4
20lg 2T 2 1
2
近似曲线 精确曲线
对数幅频特性和相频特性：
L() 20 lg 1 (T )2 () tg1 T
0 L0 0
1 L 20 lg 1 3
T
2
4
L
2
L()(dB) 0 0.1 5
10 15 20
0.2
0.3 0.4
0.6 0.8 1
T
2
34
6 8 10
七、一阶不稳定环节
传递函数: G s 1
Ts 1
➢1. 幅相频率特性
频率特性: G j 1
jT 1
G j
1
jT 1
1
1 T2
T
j1 T2
U
jV
U
1 2
2
V
2
1 2
2
一阶不稳定系统的幅相频
率特性是一个为（-1，j0）
为圆心，0.5为半径的半圆。
180O 90O
Im
1

典型环节示例 1 比例环节
输出量不失真、无惯性地跟随输入量， 两者成比例关系。
传递函数及典型环节的传递函数
比例环节的传递函数为：
传递函数及典型环节的传递函数
2 惯性环节： 凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数） T—时间常数，表征环节的惯性，和 环节结构参数有关
传递函数及典型环节的传递函数
如：有源积分网络
传递函数及典型环节的传递函数
液压缸
传递函数及典型环节的传递函数
5 二阶振荡环节 含有两个独立的储能元件，且所存储的 能量能够相互转换，从而导致输出带有 振荡的性质，运动方程为：
传递函数：
传递函数及典型环节的传递函数
振荡环节传递函数的另一常用标准形式为 （K=1）
无源微分网络
无源网络
显然，无源微分网络包括有惯性环节和微 分环节，称之为惯性微分环节，只有当 |Ts|<<1时，才近似为微分环节。
传递函数及典型环节的传递函数
除了上述微分环节外，还有一类一阶微分环 节，其传递函数为：
微分环节的输出是输入的导数，即输出反 映了输入信号的变化趋势，从而给系统以 有关输入变化趋势的预告。因此，微分环 节常用来改善控制系统的动态性能。
2) 传递函数是s 的复变函数。传递函数中的 各项系数和相应微分方程中的各项系数对应 相等，完全取决于系统结构参数；
传递函数及典型环节的传递函数
3) 传递函数是在零初始条件下定义的，即在零时 刻之前，系统对所给定的平衡工作点处于相对静 止状态。因此，传递函数原则上不能反映系统在 非零初始条件下的全部运动规律； 4) 传递函数只能表示系统输入与输出的关系,无 法描述系统内部中间变量的变化情况。

[G ( jω )]
1
ω →∞
0
G ( jω ) =
(1 − T ω ) + (2ζTω )
2 2 2
1
2
ωn ωn ωn
1 ω ≤ T
ς↑
ω →0
ς↓
2ζTω − arctan 1 − T 2ω 2 ∠ G ( jω ) = 2ζTω − π − arctan 1 − T 2ω 2
6、勾画出大致曲线。
①
②
当频率ω = 0 时，其开环幅相特性完全由比例环节和积分环 节决定。 节决定。 G 开环传递函数不含积分环节， 开环传递函数不含积分环节，即v = 0 时，( jω ) 曲线从正实 开始； 轴 开始；G ( j0) = K∠0° G 开环传递含有一个积分环节， 开环传递含有一个积分环节，即 v = 1 时， ( jω ) 曲线从负虚 π G 轴方向开始； 轴方向开始； ( j 0 ) = ∞ ∠ − 2 π G 曲线从负实轴方向开始； 当 v = 2 时，曲线从负实轴方向开始； ( j 0 ) = ∞∠ − 2 2 其余依次类推。 其余依次类推。 ，（即 中分母阶次n 当频率 ω = ∞ 时，若 n > m ，（即 G ( s ) 中分母阶次 大 于分子阶次m） 的模值等于0， 于分子阶次 ）其 G ( jω ) 的模值等于 ，相为 ( m − n ) π 。 2 即 π G ( j ∞ ) = 0∠ ( m − n ) 2
G ( jω) = G ( jω) e j∠G( jω) = u (ω) + jv (ω)
a) 令∠G ( jω ) = −π 。解出与负实轴交点处对应的频率 ω x 的值。再将 ω x 代入 G ( j ω ) 中，求得与负实轴交 的值。 点的模值。 点的模值。 b) 令 v (ω ) = 0 解出 ω x ，再将 ω x 代入 u (ωx ) 中求得与负 实轴交点的坐标。 实轴交点的坐标。