下载文档原格式
2-6 传递函数求解控制系统的微分方程，可以得到在确定的初始条件及外作用下系统输出响应的表达式，并可画出时间响应曲线，因而可直观地反映出系统的动态过程。
如果系统的参数发生变化，则微分方程及其解均会随之而变。
为了分析参数的变化对系统输出响应的影响，就需要进行多次重复的计算。
微分方程的阶次愈高，这种计算愈复杂。
因此，仅仅从系统分析的角度来看，就会发现采用微分方程这种数学模型，当系统阶次较高时，是相当不方便的。
以后将会看到，对于系统的综合校正及设计，采用微分方程这一种数学模型将会遇到更大的困难。
目前在经典控制理论中广泛使用的分析设计方法——频率法和根轨迹法，不是直接求解微分方程，而是采用与微分方程有关的另一种数学模型——传递函数，间接地分析系统结构参数对响应的影响。
所以传递函数是一个极其重要的基本概念。
一、传递函数的概念及定义在[例2-7]中，曾建立了RC 网络微分方程，并用拉氏变换法对微分方程进行了求解。
其微分方程（2-44）为)()(t u t u dtdu RC r c c =+ 假定初始值0)0(=c u ，对微分方程进行拉氏变换，则有)()()1(s U s U RCs r c =+网络输出的拉氏变换式为)(11)(s U RCs s U r c += （2-48）这是一个以s 为变量的代数方程，方程右端是两部分的乘积；一部分是)(s U r ，这是外作用（输入量）的拉氏变换式，随)(t u r 的形式而改变；另一部分是11+RCs ，完全由网络的结构参数确定。
将上式（2-48）改写成如下形式 11)()(+=RCs s U s U r c 令11)(+=RCs s G ，则输出的拉氏变换式可写成 )()()(s U s G s U r c =可见，如果)(s U r 给定，则输出)(s U c 的特性完全由)(s G 决定。
)(s G 反映了系统（网络）自身的动态本质。
这很显然，因为)(s G 是由微分方程经拉氏变换得到的，而拉氏变换又是一种线性变换，只是将变量从实数t 域变换（映射）到复数s 域，所得结果不会改变原方程所反映的系统本质，对照)(s G 与原微分方程（2-44）的形式，也可看出二者的联系。
第六章 传递函数对于线性定常系统，传递函数是常用的一种数学模型，它是在拉氏变换的基础上建立的。
用传递函数描述系统可以免去求解微分方程的麻烦，间接地分析系统结构及参数与系统性能的关系，并且可以根据传递函数在复平面上的形状直接判断系统的动态性能，找出改善系统品质的方法。
因此，传递函数是经典控制理论的基础，是一个极其重要的基本概念。
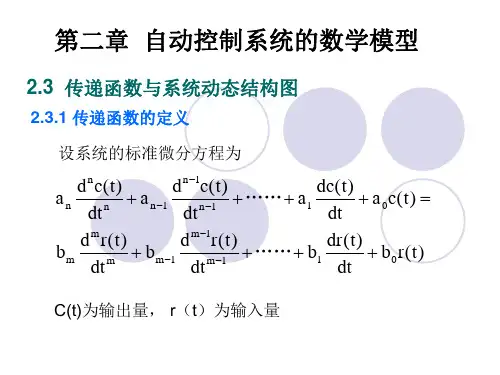
第一节 传递函数的定义一、传递函数的定义1、定义对于线性定常系统，在零初始条件下，系统输出量的拉氏变换与输入量的拉()()C s R s ==零初始条件输出信号的拉氏变换传递函数输入信号的拉氏变换2、推导设线性定常系统的微分方程的一般形式为1011110111()()()()()()()()n n n n nn m m m m mm d d d a c t a c t a c t a c t dtdtdtd d d b r t b r t b r t b r t dtdtdt------++⋅⋅⋅++=++⋅⋅⋅++◆ 式中c(t)是系统输出量，r(t)是系统输入量，r(t)、c(t)及其各阶导数在t=0时的值均为零，即零初始条件。
◆a ， 1a ，…，na 及b ， 1b ，…，mb 均为系统结构参数所决定的实常数。
对上式中各项分别求拉氏变换，并令C(s)＝L[c(t)]，R(s)=L[r(t)]，可得s 的代数方程为：11011011[]()[]()nn mm n n m m a s a sa s a C sb sb sb s b R s ----++⋅⋅⋅++=++⋅⋅⋅++于是，由定义得到系统的传递函数为：10111011()()()()()m m m m nn n nb s b sb s b C s M s G s R s a s a sa s a N s ----++⋅⋅⋅++===++⋅⋅⋅++其中，1011()m m m m M s b s b s b s b --=++⋅⋅⋅++ 1011()n n n n N s a s a s a s a --=++⋅⋅⋅++ N(s)=0称为系统的特征方程，其根称为系统特征根。
