典型环节传递函数-积分环节

控制工程基础基本知识与公式

控制工程基础基本知识与公式
控制以测量反馈为基础，控制的本质是检测偏差，纠正偏差。

自动控制系统的重要信号有输入信号、输出信号、反馈信号、偏差信号等。

输入信号又称为输入量、给定量、控制量等。

自动控制按有无反馈作用分为开环控制与闭环控制。

自动控制系统按给定量的运动规律分为恒值调节系统、程序控制系统与随动控制系统。

自动控制系统按系统线性特性分为线性系统与非线性系统。

自动控制系统按系统信号类型分为连续控制系统与离散控制系统。

自动控制系统按系统输入输出变量数量分为单变量系统与多变量系统。

对控制系统的基本要求是稳定性、准确性、快速性。

拉普拉斯变换：
拉普拉斯反变换
拉普拉斯变换解微分方程传递函数是在零初始条件下将微分方程作拉普拉斯变换，进而运算而来。

传递函数与微分方程是等价的。

传递函数适合线性定常系统。

)a s (F )t (f e at +→-
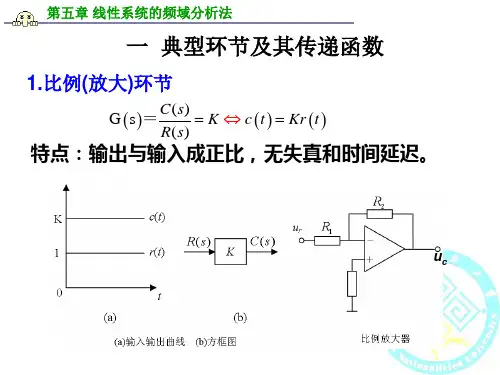
典型环节传递函数：
比例环节K 惯性环节
一阶微分环节二阶微分环节传递函数框图的化简
闭环传递函数开环传递函数误差传递函数闭环传递函数是输出信号与输入信号间的传递函数。

误差传递函数又称偏差传递函数，是偏差信号与输入信号间的传递函数。

系统输出信号称为响应，时间响应由瞬态响应与稳态响应组成。

系统的特征方程是令系统闭环传递函数分母等于零而得。

特征方程的根就是系统的极点。

1S +τ
1
S 2S 22+ζτ+τ
一阶惯性系统
的单位阶跃响应：。

大学自动控制原理2.4典型环节传递函数

02
传递函数的零点和极点决定了系统的动态特性和稳定性。
03
传递函数的分子和分母多项式决定了系统的频率响应特性。
典型环节的分类
比例环节
输出信号与输入信号成正比，传递函数为 G(s) = K，其中 K 为常数。
02
积分环节
输出信号与输入信号的时间积分成正比，传递函数为 G(s) = 1 / (sT)，其中 T 为时间常数。
将介绍控制系统的稳定性分析方法。
掌握频率响应法在控制系统设计中的应用。
学习如何利用根轨迹法进行系统性能分析。
了解现代控制系统的基本概念和分类。
THANKS FOR WATCHING
感谢您的观看
高阶环节的传递函数具有多个极点和零点，这些极点和零点决定了环节的动态特性，如响应速度、超调和调节时间等。
实例分析
以一个三阶惯性环节为例，其传递函数为 $G(s) = frac{1}{s^3 + 2s^2 + 3s + 1}$，该环节具有三个极点 $s = -1, -1, -1$ 和一个零点 $s = 0$。
拉普拉斯变换中的频率。
该传递函数是一个有理分式，分母为线性多项式，分子为常数。
当输入信号 (s) 变化时，输出信号 (G(s)) 会根据增益 (K) 和时间
常数 (T) 进行相应的变化。
实例分析
实例1
一阶惯性环节在电机控制系统中的应用，用于描述电机的动态响应特性。
实例2
在温度控制系统中的一阶惯性环节，用于描述加热元件的热量传递和散热过程。
04 一阶惯环节
定义与特点
定义
一阶惯性环节的传递函数为 (G(s) = frac{K}{T s + 1})，其中 (K) 是增益，(T) 是时间常数。

典型环节与开环系统的频率特性

第五章线性系统的频域分析法
6.一阶微分环节和二阶微分环节
dr (t ) G s ＝Ts +1 c(t ) T r (t ) dt
C(s) G s ＝ T 2 s 2 + 2 Ts 1 R(s)
2 d r (t ) dr (t ) 2 c(t ) T 2 T r (t ) 2 dt dt
传函典型环节表达式
第五章线性系统的频域分析法
二典型环节极坐标(Nyquist)图的绘制
1.放大环节（比例环节）
传递函数：G(s) K 频率特性： G( j) [G(s)]s j K Ke j 0 K j0
A( ) K ( ) 0
Im
放大环节的极坐标图是复平面实轴上的一个点，它到原点的距离为K。
第五章线性系统的频域分析法
G(j0) 1 0
1 1 G j 45 2 T
G(j) 0 -90
不难看出，随着频率 ω=0→∞ 变化，惯性环节的幅值逐步衰减，最终趋于 0 。相位的绝对值越来越大，但最终不会大于90°，其极坐标图为一个半圆。
Im

s
实际微分环节实现电路
第五章线性系统的频域分析法
4.积分环节
1 1 G s ＝ c t r t dt Ti s Ti 特点：输入消失后输出仍具有记忆功能。
dt
0
t
实例：电动机角速度与角度间的关系，物体行驶距离与物体速度间的关系，模拟计算机中的积分器等。
特点：含一个储能元件，对突变的输入不能立即跟随，输出无振荡。
0.63
第五章线性系统的频域分析法
3.微分(超前)环节

控制工程基础：2.4 传递函数以及典型环节的传递函数

(s+pj )
j 1
m
(is 1)
K
i1 n
(Tjs 1)
j 1
(零极点形式、首一多项式形式、伊万思形式)
(时间常数形式、尾一多项式形式、伯德形式)
(动态)方框图： R(s)
C(s)
G(s)
m
G(s)
C(s) R(s)
b0sm b1sm1 bm1s bm a0sn a1sn1 an1s an
举例
2、用复阻抗概念求电路的传递函数
L
R2
＋
＋
ur
u1 R1 C
－
－
Ls
R2
＋
＋
＋
uc Ur(s) U1(s) R1 1/Cs
－
－
－
＋
Uc(s)
－
举例
RLC网络示意图
3、等效刚度法
设等效弹性刚度为：fa
f1
k1
→ 则 fa =k1+f1s
并联弹簧的弹性刚度等于各弹簧弹性刚度之和。
k2 设等效弹性刚度为：fb
R(0)
s0 an r()
传递函数的阶：特征多项式的阶次n即为传递函数的阶次，对应的系统为n阶系统。
二、传递函数的性质
性质1：传递函数是复变量s的有理真分式函数，所有的系数均为实常数，且m≤n。
性质2：传递函数由系统的结构和参数确定，与输入信号的形式与大小无关。
性质3：如果传递函数已知，那么可以研究系统在各种输入信号作用下的输出响应。
N(s) – 分母多项式，又称特征多项式，它决定着系统响应的基本特点和动态本质。
一般情况下，要求n≥m
G(s) C(s) b0sm b1s m1 bm1s bm M (s) R(s) a0s n a1s n1 an1s an N (s)

典型环节的时域响应实验

典型环节的时域响应实验一、实验目的1、熟悉并掌握自动控制原理实验系统的使用方法及各典型环节模拟电路的构成方法。

2、熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。

对比差异、分析原因。

3、了解参数变化对典型环节动态特性的影响，掌握各典型环节的工作特点。

二、实验设备1、自动控制原理实验箱2、示波器三、实验原理典型环节分别有比例、积分、微分、惯性、比例积分、比例微分、比例积分微分等环节，在不同输入信号下将会有不同的输出响应，呈现出不同的工作特点，其方框图、传递函数、模拟电路等如下所示：1、比例环节(P)（1）方框图：如图1.1-1所示。

（2）传递函数：（3）阶跃响应：（4）模拟电路图：如图1.1-2所示。

注意：图中运算放大器的正相输入端已经对地接了100K的电阻，实验中不需要再接。

以后的实验中用到的运放也如此。

（5）理想与实际阶跃响应对照曲线：①取R0=200K；R1=100K。

理想阶跃响应曲线实测阶跃响应曲线②取R0=200K；R1=200K。

理想阶跃响应曲线实测阶跃响应曲线2、积分环节(I)（1）方框图：如右图1.1-3所示。

（2）传递函数：（3）阶跃响应：（4）模拟电路：如图1.1-4所示。

（5）理想与实际阶跃响应曲线对照：①取R0=200K；C=1uF。

理想阶跃响应曲线实测阶跃响应曲线②取R0=200K；C=2uF。

理想阶跃响应曲线实测阶跃响应曲线3.比例积分环节(PI)(1)方框图：如图1.1-5所示。

（2）传递函数：（3）阶跃响应：（4）模拟电路图：如图1.1-6所示。

（6）理想与实际阶跃响应曲线对照：①取R0=R1=200K；C=1uF。

理想阶跃响应曲线实测阶跃响应曲线②取R0=R1=200K；C=2uF。

理想阶跃响应曲线实测阶跃响应曲线4.惯性环节(T)（1）方框图：如图1.1-7所示。

（2）传递函数：（3）模拟电路图：如图1.1-8所示。

（4）理想与实际阶跃响应曲线对照：①取R0=R1=200K；C=1uF。

2-4 典型环节及其传递函数

1
气阻的数学表达式为 ∆p = R∆q ∆p 式中，是气体压力降； ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量； R 是气阻值。因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) （３）喷嘴一挡板机构喷嘴一挡板机构由恒节流孔１，背压室２，喷嘴３，和挡板４组成，如图２－１８所示。 ∆h 它的作用是把输入挡板的微小位移转换成相应的气压信号输出。在忽略背压室气容影响时，可把喷嘴 1 2 4 一挡板机构看作一个比例环节，即 3 D ∆p D = k 1 ∆h 式中，是喷嘴背压的变化； ∆p D ∆h 是挡板开度变化量；是比例系数。 k1 d （４）放大器 h 在自动控制系统中用得最多的是运算放大器，它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室运算放大器一般由集成电路构成，其符号如图２－ 3 − 喷嘴 4 − 挡板１９所示。图 2-17 喷嘴挡板机构结构示意图图中三角形尖端代表输出端，输出电压为 u 0 (t ) 它有两个输入端，一个是同相输入端ｂ用 “十”表示，一个是反相输入端ａ用“一”表示。当放大器工作在放大区而不是饱和区时，输出电压与同相输入端电压和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中，为开环放大倍数，这个数值很高，可达到。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点： ①由于开环输入电阻很高，运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高，所以ｂ端和Ｃ端电位接近相等，即。 u i2 ≈ ui1 运算放大器本身虽属放大环节，但可用它来组成其他各种基本环节。

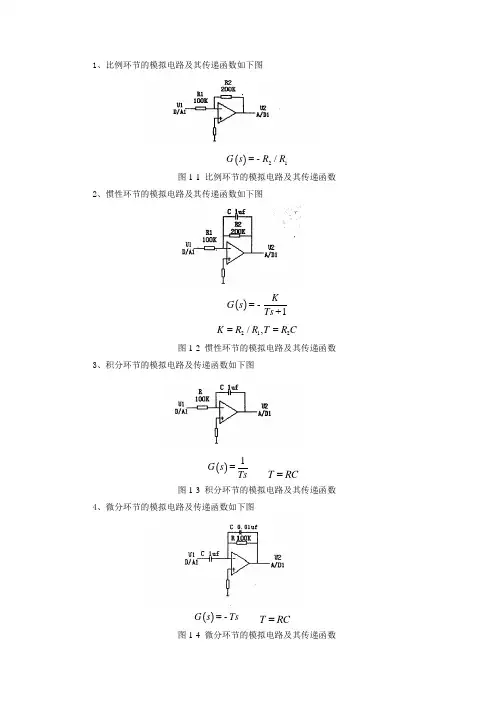
典型环节的模拟电路

1、比例环节的模拟电路及其传递函数如下图
()21/G s R R =-
图1-1 比例环节的模拟电路及其传递函数
2、惯性环节的模拟电路及其传递函数如下图
()1K
G s Ts =-+
212/,K R R T R C ==
图1-2 惯性环节的模拟电路及其传递函数
3、积分环节的模拟电路及传递函数如下图
()1
G s Ts = T R C =
图1-3 积分环节的模拟电路及其传递函数
4、微分环节的模拟电路及传递函数如下图
()G s Ts =- T R C = 图1-4 微分环节的模拟电路及其传递函数
5、比例+微分环节的模拟电路及传递函数如下图（未标明的C=0.01f ）。

()()
2121/,G s K Ts K R R T R C =-+==
图1-5 比例+微分环节的模拟电路及其传递函数
6、比例+积分环节的模拟电路及传递函数如如下图
()()
2121/,G s K Ts K R R T R C =-+==
图1-6 比例+积分环节的模拟电路及其传递函数
7、重点：典型环节在阶跃输入信号作用下的输出特性测试。

8、难点：掌握典型环节的电模拟方法及其参数测试方法，测量典型环节的阶跃响应曲线，了解参数变化对动态特性的影响。

难点：参数变化对动态特性的影响。

2-4 典型环节及其传递函数

∫
G ( s ) = R / Ts ，这也是一个积分环节。从物理意义上说，由于液箱的液容Ｃ太大，或液阻Ｒ
太大，液箱流出水量不足以影响液位，如果流入水量不变，液位将随时间不断增高（积分作用）。另外对直流伺服电动机，由于电气时间常数和机电时间常数大小，忽略不计时，该电动机以转速为输出量，电枢电压为输入量时的动态特性成为比例环节，其传递函数为 N (s) G( s ) = =k U a (s) 如以电动机输出轴转角为输出量，相应的传递函数是 a ( s) k G( s ) = = U a (s) s 这是一个积分环节。可见，对于同一部件，不同输入或不同输出时，其传递函数是不同的。最后，考虑气动仪表中常用的气容，它是一个气体容室能储存或放出气体，对气体量的变化起惯性作用，类似于电路中的电容，见图２－２０。通常采用“气容”这个概念来定量地表示气室储存气体的能力，其定义为 ∆m C= ∆p 式中，是空气储存量的增量； ∆m ∆p 是气室压力的增量。气体的质量流量（ｋｇ／ｓ）为 ∆q (t ) = d (∆m ) / dt
5
R2 R1
Ui Ri
图 2-23 运算放大器组成的一阶惯性环节
−
+
C
U0
式中，时间常数Ｔ＝ＲＣ。实际上这是纯微分环节与一阶惯性环节相串联后构成的环节；当时间常数Ｔ＜＜１时，一阶惯性环节相当于１：１的比例环节，因而总的传递函数相当于微分环节的传递函数。当然也可以用运算放大器来组成微分环节，如 R 图２－２４所示。该运放电路的传递函数为 if C U 0 (s) Ui G( s ) = = − RCs U i (s) U0 这就相当于一个纯微分环节。 + i
−
2

典型环节的传递函数

典型环节的传递函数
1、比例环节凡输出量与输入量成正比，输出不失真也不延迟而按比例地反映输入的环节，称为比例环节又叫放大环节、无惯性环节、零阶环节
•动力学方程为：
xotKxit
•传递函数为：
Gs
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比，称为积分环节，又称为理想积分环节
•动力学方程为：
Tdxdottxotxit
•传递函数为：
GsXXoi ss
1 Ts1
典型环节的传递函数
5、导前环节(一阶微分环节) 又称为一阶微分环节，是一个相位超前环节。
•传递函数为：
GsXXoi ssTs1
典型环节的传递函数
6、振荡环节(二பைடு நூலகம்积分环节) 振荡环节是二阶环节，又称二阶振荡环节
•传递函数为：
•动力学方程为：
xotT1xi tdt
•传递函数为：
Gs
Xo s Xi s
1 Ts
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比，称为微分环节，又称为理想微分环节
•动力学方程为：
xo
t
T
dxi t
dt
•传递函数为：
Gs
Xo s Xi s
Ts
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节，是一个相位滞后环节。
G sX Xo isss22 n 2 nsn 2
GsX Xo issT2s22 1Ts1
典型环节的传递函数
7、二阶微分环节
•传递函数为：
G sX Xo isss22 n 2 nsn 2 GsX Xo issT2s22Ts1

第二章典型环节的数学模型(2-1)

18
电机运动方程
1） T(t)=Ki(t) 2） e (t) K d (t)
b b
dt
T(t)——转矩 K——力矩系数 eb(t)——反电势 Kb——反电势常数 ea(t)——电枢两端的电压
i a (t )
R
3） L di(t) Ri(t) e (t) e (t) b a
dt
4）
2
传递函数：
R(s)
1 T 2 s 2 2 Ts 1
C ( s)
式中：——阻尼比， T——振荡环节的时间常数。频率特性： C ( j ) 1
G ( j ) R ( j ) (1 T 2 2 ) j 2 T
16
R
L
+
i (t )
+
例：RLC电路
r(t)
_
C
传递函数：
I(s) s 1 （R=1 U(s)
RC= ）
频率特性：
G jω 1 jω
一阶微分环节可看成一个微分环节与一个比例环节的并联，其传递函数和频率特性是惯性环节的倒数。
24
7、二阶微分环节
特点：输出量与输入量及输入量的一阶、二阶导数都有关运动方程： 2
d r(t ) dr(t ) c(t ) T 2ζ T r(t ) 2 dt dt
+ _
D
J
B
19
消去中间变量Eb(s)、T(s)和I(s)
θ (s) K E a (s) s[LJs2 (LB RJ)s (RB KK b )]
如果输入量Ea(s)，输出量转速(s)，则又可得到：
(s) K E a (s) LJs 2 (LB RJ)s (RB KK b )

典型环节的传递函数

i (t)
对于相同量纲的理想微分环节物理上是难以实现的，电路中常遇到下述的近似微分环节。 2 近似微分环节
u i (t)
i (t ) ——输入转角；其中， u0(t) ——输出电压。
图永磁式直流测速机
G(s)
kTs Ts 1
1 u ( t ) i(t )dt i(t )R 已知 i C u 0 (t ) i(t )R
只有当|Ts|<<1时，才近似为微分环节。
（4）积分环节
如果输出变量正比于输入变量的积分，即进行拉氏变换得 X 0 (s) k
x 0 ( t ) k x i ( t )dt
G (s) X 0 (s ) k X i (s ) s

则
X i (s) s
特点：系统的输出和输入之间没有唯一对应的关系，有记忆功能，能提高系统的稳态精度，系统中的积分环节不能大于2个，否则系统不稳定。
F s kX s
k
阻尼器
D
x(t)
t f t Dx
F s DsX s
Ds
质量
M
x(t)
t f t M x
F s Ms 2 X s
Ms 2
等效复阻抗
xi (t )
x0 (t )
k
数学模型为 o cx o kxo kxi m x (m s cs k ) X o ( s) kX i ( s)
(2)一阶惯性环节凡运动方程为下面一阶微分方程
T d xo (t ) xo (t ) Kxi (t ) dt
形式的环节称为一阶惯性环节。其传递函数为：
G( s) X o ( s) K X i ( s ) Ts 1

自动控制原理--典型环节的频率特性

j
j 1
0j 1
Im
0
Re
0
积分与微分环节
L(dB) 40
积分环节
0
微分环节
40
( )
90
微分环节
0 90
积分环节
20dB / dec
20dB / dec
6
三、微分环节
传递函数: G s s
频率特性:
G(j)
j
ej
π 2
➢1. 幅频特性 A及相频特性
A ,
A
( )
0
1
T
4
2
L,
0
1
T 3dB
4
20lg 2T 2 1
2
近似曲线精确曲线
对数幅频特性和相频特性：
L() 20 lg 1 (T )2 () tg1 T
0 L0 0
1 L 20 lg 1 3
T
2
4
L
2
L()(dB) 0 0.1 5
10 15 20
0.2
0.3 0.4
0.6 0.8 1
T
2
34
6 8 10
七、一阶不稳定环节
传递函数: G s 1
Ts 1
➢1. 幅相频率特性
频率特性: G j 1
jT 1
G j
1
jT 1
1
1 T2
T
j1 T2
U
jV
U
1 2
2
V
2
1 2
2
一阶不稳定系统的幅相频
率特性是一个为（-1，j0）
为圆心，0.5为半径的半圆。
180O 90O
Im
1

2.4传递函数及典型环节传递函数

典型环节示例 1 比例环节
输出量不失真、无惯性地跟随输入量，两者成比例关系。
传递函数及典型环节的传递函数
比例环节的传递函数为：
传递函数及典型环节的传递函数
2 惯性环节：凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数） T—时间常数，表征环节的惯性，和环节结构参数有关
传递函数及典型环节的传递函数
如：有源积分网络
传递函数及典型环节的传递函数
液压缸
传递函数及典型环节的传递函数
5 二阶振荡环节含有两个独立的储能元件，且所存储的能量能够相互转换，从而导致输出带有振荡的性质，运动方程为：
传递函数：
传递函数及典型环节的传递函数
振荡环节传递函数的另一常用标准形式为（K=1）
无源微分网络
无源网络
显然，无源微分网络包括有惯性环节和微分环节，称之为惯性微分环节，只有当 |Ts|<<1时，才近似为微分环节。
传递函数及典型环节的传递函数
除了上述微分环节外，还有一类一阶微分环节，其传递函数为：
微分环节的输出是输入的导数，即输出反映了输入信号的变化趋势，从而给系统以有关输入变化趋势的预告。因此，微分环节常用来改善控制系统的动态性能。
2) 传递函数是s 的复变函数。传递函数中的各项系数和相应微分方程中的各项系数对应相等，完全取决于系统结构参数；
传递函数及典型环节的传递函数
3) 传递函数是在零初始条件下定义的，即在零时刻之前，系统对所给定的平衡工作点处于相对静止状态。因此，传递函数原则上不能反映系统在非零初始条件下的全部运动规律； 4) 传递函数只能表示系统输入与输出的关系,无法描述系统内部中间变量的变化情况。

典型环节

[G ( jω )]
1
ω →∞
0
G ( jω ) =
(1 − T ω ) + (2ζTω )
2 2 2
1
2
ωn ωn ωn
1 ω ≤ T
ς↑
ω →0
ς↓
2ζTω − arctan 1 − T 2ω 2 ∠ G ( jω ) = 2ζTω − π − arctan 1 − T 2ω 2
6、勾画出大致曲线。
①
②
当频率ω = 0 时，其开环幅相特性完全由比例环节和积分环节决定。节决定。 G 开环传递函数不含积分环节，开环传递函数不含积分环节，即v = 0 时，( jω ) 曲线从正实开始；轴开始；G ( j0) = K∠0° G 开环传递含有一个积分环节，开环传递含有一个积分环节，即 v = 1 时， ( jω ) 曲线从负虚 π G 轴方向开始；轴方向开始； ( j 0 ) = ∞ ∠ − 2 π G 曲线从负实轴方向开始；当 v = 2 时，曲线从负实轴方向开始； ( j 0 ) = ∞∠ − 2 2 其余依次类推。其余依次类推。，（即中分母阶次n 当频率 ω = ∞ 时，若 n > m ，（即 G ( s ) 中分母阶次大于分子阶次m）的模值等于0，于分子阶次）其 G ( jω ) 的模值等于，相为 ( m − n ) π 。 2 即 π G ( j ∞ ) = 0∠ ( m − n ) 2
G ( jω) = G ( jω) e j∠G( jω) = u (ω) + jv (ω)
a) 令∠G ( jω ) = −π 。解出与负实轴交点处对应的频率 ω x 的值。再将 ω x 代入 G ( j ω ) 中，求得与负实轴交的值。点的模值。点的模值。 b) 令 v (ω ) = 0 解出 ω x ，再将 ω x 代入 u (ωx ) 中求得与负实轴交点的坐标。实轴交点的坐标。

自动控制原理_2.4典型环节传递函数

B盘以角速度ω 转动时，因 B盘和I 轴
间以滑动键联接，故B盘滑动就会改变
偏心量e；当时e=0，A盘转动而 B盘不
转；e增大， B盘角速度ω 正比的增大，设K为比例常数，B盘转角为θ (t)。输入— e 输出—θ (t)
解： (t ) Ke(t )
(t ) K e(t )dt
di(t ) 1 ui (t ) L i(t ) R i(t )dt dt C 1 uo (t ) i(t )dt C
§2.4.6 延时环节（迟延环节）
xo (t ) xi (t )
τ为延迟时间
L[ x0 (t )] L[ xi (t )] G( s ) L[ xi (t )] L[ xi (t )]
当|Ts|<<1时，G(s)=Ts，
才近似为理想的微分环节。
此系统为包含有惯性环节及微分环节的系统。
（1）预见输入（ቤተ መጻሕፍቲ ባይዱ输入提前）
比例环节
R(s) r(t) t
1
1
X o ( s)
xo (t )
o
45
t

比例+微分
R(s) r(t ) t
1 Ts
X o ( s)
xo (t )
K G( s ) Ts 1
K为惯性环节的增益或放大系数；T为时间常数
理想的一阶惯性环节
1 G( s ) Ts 1
例1. 无源滤波电路
ui uo C为电容 R为电阻
1 ui (t ) i (t ) R i (t )dt C 解： 1 uo (t ) i (t )dt C 1 U i (t ) I ( s) R I (s) Cs LT得： 1 U o (t ) I ( s) Cs

第二章5典型环节

当从 0—→∞变化时，频率特性曲线在第三、四象限。
与虚轴交于(

1
2
)。
Nyquist图：
特点：
0.5
0
∞ Im
0
1
Re
-0.5
2
越小，曲线与横轴 -1
围成的面积越大；
谐振频率r
-1.5
越接近固有频率n
-2 -1
1 － 2
-0.5
jik 06
0.7 0.5
Nyquist图：
趋势：当从 0—→∞变化时，G( j) 逐渐减
小到 0 ，相位从0o逐渐变到－ 90o。Im
特点：半圆，园心为 (K ，j0)，半径为 K 。
2
2
∵ν(ω)总是小于零，∴曲线是下半圆。
Page: 10
G ( j ) K Re
K2

思考∶若图形为上半圆，其频率特性应是怎样的?
G
180 90
- 90
(s -1 )
超前90o
jik 06
3
L(ω)
40db 20db 0db -20db --40db
Page: 4
微分环节L(ω)
G(s)=10s
0.1 0.2
12
[+20]
ω
10 20
100
G(s)= s
G(s)=0.1s
jik 06
4
Page: 5
实例：永磁式测速发电机
jik 06
dB 20 lg G
40
20
20 dB dec
T
G
(s-1)
10 T
90
45
0
(s-1 )

自动控制原理典型环节传递函数

即： x（ o t） T 1x（ i t） dt
拉氏变 :X（ os换） T 1得 X s（ i s） G(s)
1 Ts
T为积分环节的时间常数
例题：
当 A盘作恒速转动，并靠摩擦力带动
B盘以角速度ω转动时，因 B盘和I 轴
间以滑动键联接，故B盘滑动就会改变偏心量e；当时e=0，A盘转动而 B盘不转；e增大， B盘角速度ω正比的增大，设K为比例常数，B盘转角为θ(t)。输入— e 输出—θ(t)
x (t ) p1 、p2分别为油缸左、右腔
单位面积上的压力。
o xi—活塞位移 x0—油缸位移
可以认为是一个微分环节对于这两种机构求其传递函数均为激磁电压ui恒定，磁通不变。自动控制原理典型环节传递函数间以滑动键联接，故B盘滑动就会改变两者物理模型不同，但数学模型相同，
o
1Ts Xo (s)
1 (设c1) Ts1 k
§2.4.3 微分环节
微分环节具有输出正比于输入的微分
即 xo(t)T x i(t)
G(s)Xo(s)Xi(s)Ts
T为微分环节的时间常数
1、理想的微分环节 G(s) Ts
2、实际的微分环节
G(s) Ts Ts 1
3、微分环节对系统的控制作用
例1、电压下图为一直流发电机原理
解：
di(t)
1
ui(t)L dt i(t)RCi(t)dt
1
uo(t) Ci(t)d t
LT，得 U Ui0(： (ss))Lc1ssI((sIs))I(s)Rc1sI(s)
G(s)Uo(s)
1
Ui(s) LC 2sRC 1s
n1
LC R C
2L

典型环节传递函数-积分环节

4．举例
精品课件
输出量随着时间的增长而不断增加，增长的斜率为1/T。
1．微分方程
精品课件
积分环节(Integrating Element)
2．传递函数与功能框
积分环节的
功能框图
精品课件
阶跃响应
积分环节(Integrating Element)
3．动态Βιβλιοθήκη 反变换可得精品课件
积分环节(Integrating Element)
积分环节(Integrating Element)
积分环节的特点是它的输出量为输入量对时间的积累。因此,凡是输出量对输入量有储存和积累特点的元件一般都含有积分环节。如水箱的水位与水流量,烘箱的温度与热流量(或功率),机械运动中的转速与转矩,位移与速度，速度与加速度,电容的电量与电流等等。积分环节也是自动控制系统中遇到的最多的环节之一。

典型环节的频率特性

第五章频率域方法典型环节的频率特性用频率法研究控制系统的稳定性和动态响应，是根据系统的开环频率特性进行的，而控制系统的开环频率特性通常是由若干个典型环节的频率特性组成的，如直流电机的传递函数为()(1)mm K G s s T s =+可以将该传递函数分解为三个典型环节的乘积，分别是mK 放大环节：1s积分环节：11m T s +惯性环节：掌握好典型环节的频率特性，就能方便地得出系统的开环频率特性。

一、比例环节（放大环节）幅频特性()A Kω=相频特性()0ϕω︒=对数幅频特性()20lg L Kω=Kj()G s K =幅相特性曲线（K>0）（Nyquist 曲线）对数频率特性曲线（K>1）（Bode 图）典型环节的频率特性20lg K/dBL ϕω2π−ω(j )G Kω=AAKϕ2π−ϕω幅频、相频特性曲线(K>0)二、积分环节1()G s s =幅频特性1()A ωω=相频特性()2πϕω=−j2π−ω=ω∞幅相特性曲线（Nyquist 曲线）1()20lg20lg L ωωω==−对数幅频特性对数幅频特性曲线是斜率为-20分贝/十倍频程的直线，该直线在弧度/秒处与零分贝线相交。

1ω=1(j )j G ωω=AAϕ2π−ϕω幅频、相频特性曲线/(rad/s)ω对数频率特性曲线（Bode 图）20dB/dec−/dBL o /()ϕ三、惯性环节（一阶系统）1()1G s Ts =+幅频特性21()()1A T ωω=+相频特性()arctan T ϕωω=−幅相频特性曲线（Nyquist 曲线）j=1/Tω=ω∞=0ωω1-45︒1(j )1+j G T ωω=Aϕ90︒−ϕω145︒−1TA幅频、相频特性曲线对数频率特性曲线（Bode 图）T ω/dBL o /()ϕ2()20lg ()1L T ωω=−+对数幅频相频特性()arctan T ϕωω=−3(dB)L =−45ϕ︒=−当频率时1T ω=2()20lg ()1L T ωω=−+对数幅频()20lg 20lg 20lg L T Tωωω≈−=−−转折频率：1=Tω当频率时1T ω<()20lg10 (dB)L ω≈=当频率时1T ω>惯性环节（一阶系统）1()1G s Ts =+1(j )1+j G T ωω=对数频率特性曲线（Bode 图）T ω 20dB/dec−对数幅频渐近特性曲线3(dB)−dBL /o /()ϕ四、振荡环节（二阶系统）222()2nn nG s s s ωζωω=++2221()[1()][2()]n n A ωωωζωω=−+22()()arctan 1()n n ζωωϕωωω⎛⎫=− ⎪−⎝⎭/nωωA=0ζ=0.2ζ=0.5ζ=0.7ζ=1ζ/nωωo /()ϕ(0) 1 ()1(2) ()0n A A A ωζ==∞=()0d A d ωω=212m nωωζ=−令，得20<<2ζ⎛⎫ ⎪ ⎪⎝⎭(0)0 ()2 ()=n ϕϕωπϕπ==−∞−21()21m m A A ωζζ==−幅频、相频特性曲线(0, 0)n ζω≥>当时，，当时无峰值。

典型环节传递函数-积分环节

合集下载

控制工程基础基本知识与公式

大学自动控制原理2.4典型环节传递函数

典型环节与开环系统的频率特性

控制工程基础：2.4 传递函数以及典型环节的传递函数

典型环节的时域响应实验

2-4 典型环节及其传递函数

典型环节的模拟电路

2-4 典型环节及其传递函数

典型环节的传递函数

第二章典型环节的数学模型(2-1)

典型环节的传递函数

自动控制原理--典型环节的频率特性

2.4传递函数及典型环节传递函数

典型环节

自动控制原理_2.4典型环节传递函数

第二章5典型环节

自动控制原理典型环节传递函数

典型环节传递函数-积分环节

典型环节的频率特性

文档推荐

最新文档

典型环节传递函数-积分环节

合集下载

控制工程基础基本知识与公式

大学自动控制原理2.4典型环节传递函数

典型环节与开环系统的频率特性

控制工程基础：2.4 传递函数以及典型环节的传递函数

典型环节的时域响应实验

2-4 典型环节及其传递函数

典型环节的模拟电路

2-4 典型环节及其传递函数

典型环节的传递函数

第二章 典型环节的数学模型(2-1)

典型环节的传递函数

自动控制原理--典型环节的频率特性

2.4传递函数及典型环节传递函数

典型环节

自动控制原理_2.4典型环节传递函数

第二章5典型环节

自动控制原理典型环节传递函数

典型环节传递函数-积分环节

典型环节的频率特性

文档推荐

最新文档

第二章典型环节的数学模型(2-1)