当前位置：文档之家 › 1.4卡诺图化简法

1.4卡诺图化简法

  • 格式：ppt
  • 大小：1.55 MB
  • 文档页数：55

下载文档原格式

  / 55

合集下载

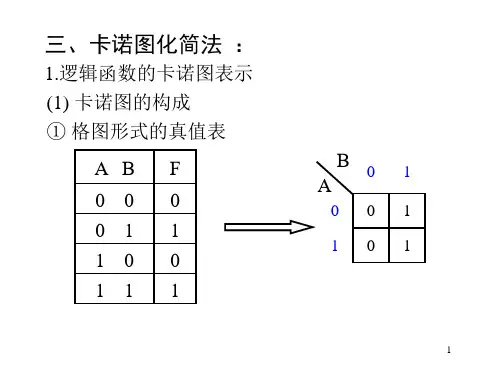
知识点3.卡诺图化简法

知识点3.卡诺图化简法

相邻项相加能消去一个因子，合并为一项，如:
。
卡诺图化简就是建立在相邻项的基础上的，消去多余的因子，使函
数得到简化。
逻辑函数的化简——卡诺图化简法
利用卡诺图化简时，首先要把函数表示成最小项之 和的形式，称为标准与或式(或最小项表达式），求函 数标准与或式有两种方法:
①从真值表中求标准与或式 ②从一般表达式利用展开法求标准与或式
逻辑函数的化简——卡诺图化简法
【例1】化简逻辑函数
化简得：
最小项合并结果有时不是唯一的，但合并后的项数和每一 项的因子数是相同的！
逻辑函数的化简——卡诺图化简法
【例2】 用卡诺图法化简逻辑函数Z（A，B，C，D）
=∑m(0，1，2，3，4，5，6，7，10，11)。
化简得：
逻辑函数的化简——卡诺图化简法
逻辑函数的化简——卡诺图化简法
利用前面介绍的公式法化简逻辑函数，要熟练掌 握逻辑代数的基本公式、常用公式和一些定律，并 且需要有一定的技巧，这对许多人来说有困难。借 助卡诺图化简逻辑函数比较方便，容易掌握。卡诺 图是美国工程师karnaugh在20世纪50年代提出的， 它建立在最小项的基础上，所以首先要了解有关最 小项的内容。
b.四个小方格组成一个大方格、或组成一行（列）、或 处于相邻两行（列）的两端、或处于四角时，所代表的最小 项可以合并，合并后可消去两个变量。
逻辑函数的化简——卡诺图化简法
c.八个小方格组成一个大方格、或组成相邻的两行 （列）、或处于两个边行（列）时，所代表的最小项可以合 并，合并后可消去三个变量。
逻辑函数的化简——卡诺图化简法
仔细分析上表，可以总结出最小项的性质： ①对任何一个最小项，只有一组变量的取值组合，使 它的值为1。反之，对于输入变量任何一组取值，有且 只有一个最小项的值为1。 ②任意两个最小项的乘积恒等于0 。 ③所有最小项之和为1。 ④具有相邻性的两个最小项之和能合并成一项且消去 一个因子。

卡诺图化简法一全文

卡诺图化简法一全文

m0
0
m1如何根据输入1变量组 m2合写出相应最2小项？
m3
3
m4
4
m5
5
m6
6
m7
7
例如 ABC 101 5 m5
m4 4 100 ABC
2. 最小项的基本性质
(1) 对任意一最小项，只有一组变量取值使它的值为1，而
其余各种变量取值均使其值为0。 (2) 不同的最小项，使它的值为1的那组变量取值也不同。 (3) 对于变量的任一组取值，任意两个最小项的乘积为0。 (4) 对于变量的任一组取值，全体最小项的和为1。
每一个与项都是最小项的与或逻辑式称为标 准与或式，又称最小项表达式。
任何形式的逻辑式都可以转化为标准与或式， 而且逻辑函数的标准与或式是唯一的。
[例] 将逻辑式 Y ABC AB C D 化为标准与或式。
解：(1) 利用摩根定律和分配律把逻辑函数式展开为与或式。
Y ABC AB C D ABC AB (C D) ABC ABC ABD 普通与或式，非标准与或式
CD
AB
C D CD CD C D
同一行最 左与最右 AB ABC D ABCD ABCD ABC D
方格相邻
AB ABC D ABCD ABCD ABC D 卡诺图特点： 循环相邻性 AB ABC D ABCD ABCD ABC D
同一列最 上与最下 ቤተ መጻሕፍቲ ባይዱ格相邻
AB ABC D ABCD ABCD ABC D
(2) 找出真值表中Y=1 对应的最小项，在 卡诺图相应方格中 填1，其余不填。
BC A 00 01 11 10
0 10 1 3 12
1 14 5 7 16
已 [例] 已知 Y AD AB(C BD)，试画出Y的卡诺图。 知 解：(1) 将逻辑式转化为与或式

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数

1.4 用卡诺图化简逻辑函数本次重点内容1、卡诺图的画法与性质2、用卡诺图化简函数 教学过程 应用卡诺图化简 一、卡诺图逻辑函数可以用卡诺图表示。

所谓卡诺图，就是逻辑函数的一种图形表示。

对n 个变量的卡诺图来说，有2n 个小方格组成，每一小方格代表一个最小项。

在卡诺图中，几何位置相邻（包括边缘、四角）的小方格在逻辑上也是相邻的。

二、最小项的定义及基本性质： 1、最小项的定义在n 个变量的逻辑函数中，如乘积项中包含了全部变量，并且每个变量在该乘积项中或以原变量或以反变量的形式但只出现一次，则该乘积项就定义为该逻辑函数的最小项。

通常用m 表示最小项，其下标为最小项的编号。

编号的方法是：最小项的原变量取1，反变量取0，则最小项取值为一组二进制数，其对应的十进制数便为该最小项的编号。

如最小项C B A 对应的变量取值为000，它对应十进制数为0。

因此，最小项C B A 的编号为m 0，如最小项C B A 的编号为m 4，其余最小项的编号以此类推。

2、最小项的基本性质：（1）对于任意一个最小项，只有一组变量取值使它的值为1，而其余各种变量取值均使它的值为0。

（2）不同的最小项，使它的值为1的那组变量取值也不同。

（3）对于变量的任一组取值，全体最小项的和为1。

图1.4.1分别为二变量、三变量和四变量卡诺图。

在卡诺图的行和列分别标出变量及其状态。

变量状态的次序是00，01，11，10，而不是二进制递增的次序00，01，10，11。

这样排列是为了使任意两个相邻最小项之间只有一个变量改变（即满足相邻性）。

小方格也可用二进制数对应于十进制数编号，如图中的四变量卡诺图，也就是变量的最小项可用m 0, m １,m ２,……来编号。

1010001111001A BCAB CD B A 0001111000011110m m m m m mmmm m m m 012300112233m m m m m m m m m m m m m m m m 456789101112131415图1.4.1 卡诺图二、应用卡诺图表示逻辑函数应用卡诺图化简逻辑函数时，先将逻辑式中的最小项(或逻辑状态表中取值为1的最小项)分别用1填入相应的小方格内，其它的则填0或空着不填。

卡诺图化简法

卡诺图化简法

26
(7) 由最大项表达式求最简与或式
例2.6.18 已知函数 F ( A, B,C, D) M (5,7,13,15)
求最简与或式。
CD AB 00 01 11 10
00 1 1 1 1 01 1 0 0 1 11 1 0 0 1 10 1 1 1 1
F(A,B,C,D) = B + D
图 2.6.18
16
(4) 合并的规律 ① 圈2格，可消去1个变量；
BC A 00 01 11 10
0 1 1 00 1 0 0 00
BC
A
00 01 11 10
0 1 0 01
1 0 0 00
F=AB
F=AC
17
② 圈4格，可消去2个变量；
ห้องสมุดไป่ตู้
BC
A
00 01 11 10
0 1 1 00
1 1 1 00
BC A 00 01 11 10
例2.6.16 化简函数
F( A, B,C, D) m(0,2,5,6,7,8,9,10,11,14,15)
为最简与或式。
CD AB 00 01 11 10
00 1 0 0 1 01 0 1 1 1 11 0 0 1 1 10 1 1 1 1
图 2.6.15
F(A,B,C,D) = A B D + BD+AB+BC
BC A 00 01 11 10 ⊕0 0 1 1 0
1 0 0 00
BC A 00 01 11 10 ﹦ 0 0 0 10
1 0 1 00
11
(4) 反演 BC
A 00 01 11 10
0 0 1 00 1 0 1 00

卡诺图化简法

卡诺图化简法

浅谈卡诺图法化简逻辑函数摘要：逻辑函数是逻辑电路设计的依据和基础，化简逻辑函数更是为节省器件，降低成本，提高效率作出了巨大贡献，而卡诺图法是化简逻辑函数最常用也是最简单的方法。

关键词：卡诺图；逻辑函数；逻辑电路；逻辑是指事物因果之间所遵循的规律。

为了避免用冗繁的文字来描述逻辑问题，逻辑代数将事物发生的原因（条件）和结果分别用逻辑函数来描述。

逻辑代数的变量和常量取值只有两种，即逻辑0和逻辑1，因而称为二值逻辑。

当然这里的0和1仅代表事物矛盾双方的两种状态，即两种对立的逻辑状态，而不是，它们可以代表事物的真表示数量的大小。

例如，它们可以代表事物的真，伪；开关的开，关；电平的高,低等。

逻辑函数可以用很多方法描述。

例如，代数法，卡诺图法，真值表法，波形图法等。

每一种描述方法都可以示电路的表逻辑功能。

但作为分析和设计逻辑电路的教学工具，节省器件，降低成本，提高工作的可靠性成为了逻辑函数至关重要的基础。

所以，化简逻辑函数便成了提高电路性能和效率必要的一步。

本文我们主要介绍的是卡诺图化简法。

一．卡诺图法的特点及化简步骤卡诺图的特点是：可以从图形上直观、清晰地反映了最小项的相邻关系，被化简函数为“与—或“形式，方法单一,易掌握，且其形式简单明了，能得到最简结果。

例如，化简函数：∑F=)7,6,4,0(m化简步骤：1.填卡诺图，即用卡诺图表示逻辑函数。

12. 画卡诺图合并相邻位置最小项郑芸莹（1989-），女，四川绵阳人，云南大学旅游文化学院信科系，研究方向：电子信息工程3.写出最简函数式。

AB C B F +=从上述的例子中看出卡诺图最小项合并的一些规律：（1）卡诺圈中小方格的个数必须为m 2个，m 2为小于或等于n 的整数。

（2）在满足规律（1）的前提下卡诺圈越大，消去的变量数越多，也就是说卡诺圈数应该尽可能的少而且要尽可能的大（但必须满足m 2个方格）。

二．卡诺图法的优缺点卡诺图的优点是简单，直观。

但当变量数超过6个时，相邻项不直观，不易找。

卡诺图化简法

卡诺图化简法

下面两个图，你会画卡诺圈吗？
CD AB 00
01 11
10
00 1 1 1 1
01 1 1 1 1
11
10
ABCD00 01 11 10
00 1
1
01 1
1
11 1
1
10 1
1
FA
FD
小结
• 1、卡诺图，用卡诺图表示逻辑函数 • 2、卡诺图法化简逻辑函数的步骤
数字电子技术
数字电子技术
目录
• 1、什么是卡诺图？ • 2、卡诺图法化简的步骤
逻辑函数卡诺图化简法
• 卡诺图是什么？
最小项 卡诺图画法规则
卡诺图表示函数
逻辑函数卡诺图化简法
•最小项： 设有 n 个变量，它们组成的“与” 项中每个变量或 以原变量或以反变量形式出现一次，且仅出现一次， 这些与项均称之为n个变量的最小项。若函数包含 n 个变量，构成的最小项应为 2n个，分别记为 mn。
③“圈1”-----用卡诺圈把相邻最小项进行合并，遵照 最大化原则；
④“读圈”----- 根据所圈的卡诺圈，消除圈内全部互 反的变量，保留相同变量作为一个“与”项。
逻辑函数卡诺图化简法
•卡诺图法化简时应遵循以下原则
① “1” 的个数为2n； ② 包围圈越大越好，个数越少越好； ③“1”可以被重复包围使用； ④必须把所有的“1”都圈完。
三变量的最小项共有23 =8个，可表示为：
ABC 000 m0 ABC 001 m1 ABC 010 m2 ABC 011 m3 ABC 100 m4 ABC 101 m5 ABC 110 m6 ABC 111 m7
逻辑函数卡诺图化简法
•卡诺图画法规则： 卡诺图是平面方格阵列图，其画法满足几何

卡诺图化简

Y ( A, B, C , D ) ABC ABCD ABCD ABCD 约束条件：A ⊙ B＝0
逻辑函数中的无关项
• 无关项在逻辑函数化简中的作用：
– 例2：用卡诺图简化下列逻辑函数，并写成最 简与或式和或与式。
Y ABC ABCD ABCD ABCD CD AB 00 约束条件：A B＝0 00 × 约束条件可表示为：AB AB 0 01 1
逻辑函数中的无关项
• 约束项：
– 表示方法：
ABC 0 ABC 0 ABC 0 ABC 0 ABC 0
或
由于约束项的值始终为 0，所以既可以将约束 项写进逻辑函数式，也 可以不写。
ABC ABC ABC ABC ABC 0
逻辑函数中的无关项
BC A 0 1
1
00
01
1 1
11
1
10
1 1
卡诺图化简法
• 利用卡诺图化简函数
– 例1：用卡诺图化简 Y AC AC BC BC
Y AC AC BC BC AC BC AB
BC A 0 1
1
00
01
1 1
11
1
10
1 1
注：卡诺图化简不是唯 一，不同的圈法得到的 简化结果不同，但实现 的逻辑功能相同的。
0
11
0
10
0
最简或与式：
Y B( A C D)( A C D)
1
0 0
1
1 0
0
1 0
1
1 0
卡诺图化简法
• 利用卡诺图化简函数
– 例3：用卡诺图化简为最简与或式和最简或与式 Y M (2,3,4,6,11,12,14)

1.4卡诺图


在合并最小项时，易忽略的两种情况： 在合并最小项时，
①卡诺图四个角上的最小项可以合并； 卡诺图四个角上的最小项可以合并； ②先画大圈，后画小圈，若出现不包括任何新的最小 先画大圈，后画小圈，
项的圈，应划掉。 项的圈，应划掉。
◆未用最小项表示的逻辑函数的化简
如果逻辑函数已经是与或表达式，则不必将其展开为 如果逻辑函数已经是与或表达式， 最小项，而将逻辑函数的各项直接填入卡诺图即可。 最小项，而将逻辑函数的各项直接填入卡诺图即可。 举例：（见P.21 例17, 演示例6） 演示例6 举例：
CD 00 AB 00 01 11 10 1 0 1 0
01 0 1 0 1
11 1 0 1 0
10 0 1 0 1
◆ 用卡诺图化简逻辑函数
基本步骤：①画出逻辑函数的卡诺图； 画出逻辑函数的卡诺图；
②合并逻辑函数的最小项； 合并逻辑函数的最小项； ③写出最简与或表达式(将合并后的最简乘积项 写出最简与或表达式( 逻辑加即可求得）。 逻辑加即可求得）。
合并的规则
在变量卡诺图中， 在变量卡诺图中 ， 凡是 几何相邻的最小项均可合 并 ， 合并时可以消去有关 变量。 变量。
m6 + m7 = ABC m8 + m12 = AC D m2 + m10 = BCD
CD 00 01 AB 11 00 0 01 4 11 12 10 8 51 13 9
11 31 71 15 11
应该注意的是：提到最小项时， 5+m6+m7 应该注意的是：提到最小项时，一定要说明变量的 该逻辑函数简写为: Y = m3+m 数目，否则，最小项这一术语将失去意义。 数目，否则，最小项这一术语将失去意义。 = Σm(3,5,6,7) 例如， 对于三个变量来说是最小项， 例如，ABC 对于三个变量来说是最小项，而 = Σ (3,5,6,7) 对于四个变量来说则不是最小项。 对于四个变量来说则不是最小项。

卡诺图化简逻辑表达式

对于包含多个非门或多个连续的与或 非门的逻辑表达式，卡诺图化简可能 无法得到最简结果。
卡诺图对于大规模逻辑电路的优化效果有限
随着逻辑电路规模的增大，卡诺图的化简过程变得复杂且耗时，难以在实际工程 中应用。
对于大规模逻辑电路，可能需要采用其他优化方法，如布尔代数、门级优化等， 以获得更好的优化效果。
THANKS
感谢观看
卡诺图化简逻辑表达式
• 卡诺图简介 • 卡诺图化简逻辑表达式的方法 • 卡诺图化简逻辑表达式的实例 • 卡诺图与其他化简方法的比较 • 卡诺图的局限性
01
卡诺图简介
卡诺图的定义
• 定义：卡诺图是一种用于表示二进制逻辑函数关系的图形表示 法，通过将逻辑函数输入变量的所有可能取值组合在网格中表 示出来，可以直观地观察到函数的最简形式。
卡诺图与布尔代数化简的比较
布尔代数化简
通过使用逻辑运算（与、或、非）的代数性质，如吸收律、分配律等，对逻辑表达式进 行简化。这种方法需要一定的数学基础，但在处理复杂逻辑表达式时可能较为繁琐。
卡诺图化简
利用图形直观地表示输入变量的所有可能组合，通过排除法简化逻辑表达式。卡诺图化 简简单易懂，不需要复杂的数学运算，特别适合初学者和解决多变量逻辑表达式的化简
问题。
卡诺图与公式化简的比较
公式化简
通过逻辑运算的公式和定理，对逻辑表达式 进行简化。这种方法需要熟练掌握各种逻辑 公式和定理，对于初学者有一定的难度。
卡诺图化简
利用图形化的方式表示输入变量的所有可能 组合，通过排除法简化逻辑表达式。卡诺图 化简直观、易于操作，不需要复杂的公式和 定理，特别适合初学者和解决多变量逻辑表 达式的化简问题。
05
卡诺图的局限性
卡诺图适用范围有限

1.4逻辑函数图形化简法


逻辑函数的图形法化简
卡诺图其实就是最小项方格图 *变量卡诺图 变量卡诺图 1. 二变量 卡诺图 二变量对应四个最小项 二变量对应四个最小项 B B A A 0 1
B
0
1
B
A 0 1
B
A AB AB
0 m0
1 m 1
A 0 1
B
0 0 2
1 1 3
A AB AB
m2
m3
将八个最小项按照逻辑相 *三变量 卡诺图： 邻性填入对应的小方格。 三变量 卡诺图： 邻性填入对应的小方格。 逻辑相邻： 逻辑相邻： 两个相邻最小项只有一 个变量不同，其它都相同。 个变量不同，其它都相同。
(1) 任一最小项，只有一组对应变量取值使其值为 1 ； 最小项， 对应规律： 0 ⇔ 反变量 对应规律：1 ⇔ 原变量 (2) 任意两个最小项的乘积为 0 ； ABC ABC AB = 1 C AB 1 。 1 0 1 C (3) 0 0 1 全体最小项之和为= 1
逻辑函数的图形法化简
3、最小项的编号： 、最小项的编号： 把与最小项对应的变量取值当成二进制数， 把与最小项对应的变量取值当成二进制数，与之 相应的十进制数，就是该最小项的编号， 表示。 相应的十进制数，就是该最小项的编号，用 mi 表示。 对应规律： 对应规律：原变量 ⇔ 1 反变量 ⇔ 0
几 何 相 邻
00 m0 m1 m3 m2 01 m4 m5 m7 m6 11 m12 m13 m15 m14 10 m8 m9 m11 m10
*五变量 *五变量 的卡诺图 对应三十二个 最小项
CDE 几何相邻 AB 000 001 011 010 110 111 101 100 00 m0 m1 m3 m2 m6 m7 m5 m4 01 m8 m9 m11 m10 m14 m15 m13 m12
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
返回
（2）最小项的表示方法 通常用符号mi来表示最小项。下标i的确定：把最小项中的 原变量记为1，反变量记为0，当变量顺序确定后，可以按顺序 排列成一个二进制数，则与这个二进制数相对应的十进制数， 就是这个最小项的下标i。 3个变量A、B、C的8个最小项可以分别表示为：
m0 A B C、m1 A BC、m 2 ABC、m3 ABC m 4 AB C、m5 ABC、m6 ABC、m7 ABC
◆ 用卡诺图化简法求最简与或表达式的步骤是：
（1）画出函数的卡诺图； （2）合并最小项； （3）写出最简与或表达式。
用卡诺图化简法求逻辑函数 F ( A, B, C, ) (1,2,3,6,7) 的最简与或表达式 解：1画出函数F 的卡诺图。对于在函数 F 的标准与或表达式中出现 的那些最小项，在其卡诺图的对应小方格中填上1，其余方格不填； 2合并最小项。把图中所有的1格都圈起来，相邻且能够合并在 一起的1 格圈在一个大圈中； 3写出最简与或表达式。对卡诺图中所画每一个圈进行合并，保 留相同的变量，去掉互反的变量。
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
Y 0 1 1 1 0 1 0 0
最小项 m0 m1 m2 m3 m4 m5 m6 m7
m1 A BC
m2 ABC
m3 ABC m5 ABC
则由真值表可得如下逻辑表达式：
Y m1 m 2 m 3 m 5 m(1,2,3,5) ABC ABC AB C ABC
BD
BD
性质3：卡诺图中八个相邻1格的最小项可以合并成一个与项， 并 消去三个变量。 综上所述，在 n 个变量卡诺图中，若有2k个1格相邻（k为 0，1，2…，n）, 它们可以圈在一起加以合并，合并时可消去 k个不同的变量，简化为一个具有(n-k)个变量的与项。若k =n，则合并时可消去全部变量，结果为1。
ABC ABC A BC A BC ABC ABC
A B C A BC ABC ABC ABC
m0 m1 m2 m3 m7
m(0,1,2,3,7)
已知真值表，写出函数的最小项之和的形式
如果列出了函数的真值表，则只要将函数值为1的那些最 小项相加，便是函数的最小项表达式。
图 三变量卡诺图
图 四变量卡诺图
补充画卡诺图。
例8 画出逻辑函数
的卡诺图。 解：
F ( A, B, C, D) m(0,1,2,5,7,8,10,11,14,15)
3. 逻辑函数的卡诺图化简法
利用卡诺图化简逻辑函数的方法称为逻辑函数的卡诺图化简法。 ◆ 卡诺图相邻性的特点保证了几何相邻两方格所代表的最小 项只有一个变量不同。因此，若相邻的方格都为1（简称1格） 时，则对应的最小项就可以合并。合并的结果是消去这个不同 的变量，只保留相同的变量。这是图形化简法的依据。 综合上述概念，卡诺图具有下述性质： 性质1：卡诺图中两个相邻1格的最小项可以合并成一个与项， 并消去一个变量。 例：
例
m1 ABC 001 m6 ABC 110
1 1 1 1 1
m2 ABC 010 m7 ABC 111
m3 ABC 011 F =（m1+m3）+（m2+m3+m6+m7）
F ( A B C A BC) ( A BC A BC ABC ABC ) AC B
【表示法2】 【表示法3】 【表示法4】 【表示法5】
m7 m6 m3 m1
m1,3,6,7
m i (i 1,3,6,7)
(1,3,6,7)
i
例：将下列函数化为最小项之和的形式
Y A BC
添项
A(B B)(C C) (A A)BC
解： 从表达式中可以看出此为四变量的逻辑函数，但是有的
乘积项中缺少一个变量，不符合最小项的规定。因此，每个乘 积项中都要将缺少的变量补上：
ABC ABC( D D) ABCD ABC D AC D AC D( B B) ABCD ABC D ABC A BC( D D) ABCD ABC D F m 0 m1 m2 m6 m8 m9 m10
性质4：全部最小项的和必为1。
（4）逻辑函数的最小项表达式 任何一个逻辑函数都可以表示成唯一的一组最小项之和，称
为标准与或表达式，也称为最小项表达式。
对于不是最小项表达式的与或表达式，可利用公式A＋A＝1
和A(B+C)＝AB＋BC来配项展开成最小项表达式。
最小项的若干表示方法
例如：
L(A, B, C) AB AC AB(C C) A(B B)C 【表示法1】 ABC ABC ABC ABC
右图为两个1格合并时消去一个变量的例 子。图中，m1和m5为两个相邻1格，则有：
m1 m5 ABC ABC ( A A)BC BC
再如：
A BCD ABCD AB C D AB CD BCD( A A) BCD AB D(C C ) AB D
二．逻辑函数的卡诺图化简法
1. 关于“最小项”
（1）最小项定义 如果一个函数的某个乘积项包含了函数的全部变量，其 中每个变量都以原变量或反变量的形式出现，且仅出现一次， 则这个乘积项称为该函数的一个标准积项，通常称为最小项。
3个变量A、B、C可组成8个最小项：
ABC、ABC、ABC、ABC、ABC、ABC、ABC、ABC
m6 0 0 0 0 0 0 1 0
m7 0 0 0 0 0 0 0 1
性质2：不同的最小项，使它的值为1的那一组变量取值 也不同。
（3）最小项的性质
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
3 变量全部最小项的真值表 ABC ABC m0 m1 m2 m3 m4 m5 m6 m7 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1BC A 0BC 0 0 0 B 0C 0 0 A AABC 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1
注意：
将真值表中函数值为0的那些最小项相加，便可得到反 函数的最小项表达式。 在n个变量的逻辑系统中，如果Y为i个最小项之和，则 Y 必为余下的（n－i）个最小项之和。
（5）最小项的相邻性
任何两个最小项如果他们只有一个因子不同，其余因子
都相同，则称这两个最小项为相邻最小项。 显然，m0与m1具有相邻性，而 m1 (A BC)与 m 2 (ABC )不相 邻，因为他们有两个因子不相同。m3与m4也不相邻，而m3与m2
相邻。
相邻的两个最小项之和可以合并成一项，并消去一个变 量。如：
m0 m 2 A B C ABC A( B B) C A C
2.卡诺图
◆ 基本知识 卡诺图是由美国工程师卡诺（Karnaugh）首先提出的一种 用来描述逻辑函数的特殊方格图。 在这个方格图中，每一个方格代表逻辑函数的一个最小项， 而且几何相邻（在几何位置上，上下或左右相邻）的小方格具 有逻辑相邻性，即两相邻小方格所代表的最小项只有一个变量 取值不同。 对于有n个变量的逻辑函数，其最小项有2n个。因此该逻 辑函数的卡诺图由 2n 个小方格构成，每个小方格都满足逻辑 相邻项的要求。 分别画出了二、三、四个变量的卡诺图。
练习：判断正确与错误 例1
错误 （多画一个圈）
正确
F BC ABC ACD AC D
F BC ACD AB D
例2
错误（圈的面积不够大） 正确
F B ABC
F B AC
例3
错误 （圈的 面积不 够大）
例4
圈错 无误 新（ 的有 一 格个 ）
F C BC D F BD ABC ACD ABC ACD
性质3：任意两个不同的最小项的乘积必为0。
（3）最小项的性质
3 变量全部最小项的真值表 A B C m0 m1 m2 m3 m4 m5 m6 m7 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 。 0 1 1 变量 0 ABC 0取值为 0 001情况下，各最小项之和为 1 0 0 0 0 1 0 0 【因为其中只有一个最小项为 0 0 0 0 1 1，其余全为 0 0 0。】 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1
（3）最小项的性质
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
3 变量全部最小项的真值表 m0 m1 m2 m3 m4 m5 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
m6 0 0 0 0 0 0 1 0
m7 0 0 0 0 0 0 0 1
性质1：任意一个最小项，只有一组变量取值使其值为1, 而在变量取其他各组值时这个最小项的值都是0。
（3）最小项的性质
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 0 1 0 1
3 变量全部最小项的真值表 m0 m1 m2 m3 m4 m5 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0