逻辑代数中的三种基本运算

1、逻辑代数有与、或和非三种基本运算。

2、四个逻辑相邻的最小项合并，可以消去__2________个因子； __2n _______个逻辑相邻的最小项合并，可以消去n 个因子。

3、逻辑代数的三条重要规则是指反演规则、代入规则和对偶规则。

4、 n 个变量的全部最小项相或值为1。

6、在真值表、表达式和逻辑图三种表示方法中，形式唯一的是真值表。

8、真值表是一种以表格描述逻辑函数的方法。

9 、与最小项ABC 相邻的最小项有AB ’C’，ABC，A’BC ’。

2n10、一个逻辑函数，如果有n 个变量，则有个最小项。

11、 n 个变量的卡诺图是由2n个小方格构成的。

13、描述逻辑函数常有的方法是真值表、逻辑函数式和逻辑图三种。

14、相同变量构成的两个不同最小项相与结果为0。

15、任意一个最小项，其相应变量有且只有一种取值使这个最小项的值为1。

1．在数字电路中，三极管主要工作在和两种稳定状态。

饱和、截止2．二极管电路中，电平接近于零时称为，电平接近于 VCC是称为。

低电平、高电平3． TTL 集成电路中，多发射极晶体管完成逻辑功能。

与运算4． TTL 与非门输出高电平的典型值为，输出低电平的典型值为。

3.6V 、 0.2V5．与一般门电路相比，三态门电路中除了数据的输入输出端外，还增加了一个片选信号端，这个对芯片具有控制作用的端也常称为。

使能端6．或非门电路输入都为逻辑 1 时，输出为逻辑。

7．电路如图所示，其输出端 F 的逻辑状态为。

18．与门的多余输出端可，或门的多余输出端可。

与有用输入端并联或接高电平、与有用输入端并联或接低电平10．正逻辑的或非门电路等效于负逻辑的与非门电路。

与非门11．三态门主要用于总线传输，既可用于单向传输，也可用于双向传输。

单向传送、双向传送12．为保证TTL 与非门输出高电平，输入电压必须是低电平，规定其的最大值称为开门电平。

低电平、开门电平13．三态门中，除了高低电平两种状态外，还有第三种状态，这第三种状态称为高阻态。

数字电路-逻辑代数基础逻辑代数基础逻辑代数中的三种基本运算与、或、⾮复合逻辑运算最常见的有与⾮、或⾮、与或⾮、异或、同或等。

异或：A⨁B=AB′+A′B同或：A⨀B=AB+A′B′异或与同或互为反运算。

逻辑代数的基本公式和常⽤公式基本公式也叫布尔恒等式（证明⽅法包括真值表法和推演法）：总结为以下⼏类：开始为0⾏1. 变量与常量间的运算规则：1、2⾏2. 重叠律（同⼀变量）：3⾏3. 互补律（变量和其反变量）：4⾏4. 交换律（5⾏）结合律（6⾏）分配律（7⾏）5. De.Morgan定理，反演律（8⾏）6. 还原律：（9）若⼲常⽤公式由基本公式导出，便于化简逻辑函数。

1. 两个乘积项相加时，若⼀项以另⼀项为因⼦，则该项多余：A+AB=A2. 两个乘积项相加时，⼀项取反后是另⼀项的因⼦，则此因⼦多余，可以消去：A+A′B=A+B3. 两个乘积项相加时，若他们分别包含B和B′两个因⼦⽽其他因⼦相同，则两项可合并。

AB+AB′=A4. 变量A和包含A的和相乘时，结果为A:A(A+B)=A5. 若两个乘积项中分别包含A和A′两个因⼦，则其余因⼦组成第三个乘积项时，第三个乘积项是多余的：AB+A′C+BC=AB+A′C进⼀步AB+A′C+BCD=AB+A′C6. A和⼀个乘积项的⾮相乘，且A为这个乘积项的因⼦时，A这个因⼦可以消去：A(AB)′=AB′7. A′和⼀个乘积项的⾮相乘，且A为这个乘积项的因⼦时，结果等于A′A′(AB)′=A′逻辑代数的基本定理代⼊定理在任何⼀个包含A的逻辑等式中，若以另外⼀个逻辑式代⼊式中所有A的位置，则等式依然成⽴。

反演定理对于任意⼀个逻辑式Y,若将其中所有的“⋅”换成“+”,“+”换成“⋅”,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到的结果就是Y′。

这个规律称为反演定理。

反演定理为求取已知逻辑式的反逻辑式提供了⽅便。

在使⽤反演定理时,还需注意遵守以下两个规则:①仍需遵守“先括号、然后乘、最后加”的运算优先次序。

逻辑代数的基本运算规则有逻辑代数是研究命题之间关系的一种代数系统，它基于集合和运算符定义了一套完备且一致的运算规则。

以下是逻辑代数的基本运算规则：1.合取（与）运算：合取是指将两个命题进行“与”的运算。

合取运算的基本规则如下：-公式化：A∧B-真假性：只有当A和B都为真时，A∧B才为真，否则为假。

-结合律：(A∧B)∧C = A∧(B∧C)-分配律：A∧(B∨C) = (A∧B)∨(A∧C)2.析取（或）运算：析取是指将两个命题进行“或”的运算。

析取运算的基本规则如下：-公式化：A∨B-真假性：只有当A和B都为假时，A∨B才为假，否则为真。

-结合律：(A∨B)∨C = A∨(B∨C)-分配律：A∨(B∧C) = (A∨B)∧(A∨C)3.非运算：非运算是指将一个命题取反的运算。

非运算的基本规则如下：-公式化：¬A-真假性：当A为真时，¬A为假；当A为假时，¬A为真。

-双重否定律：¬(¬A) = A-德摩根定律：¬(A∧B) = (¬A)∨(¬B)；¬(A∨B) = (¬A)∧(¬B)4.蕴含运算：蕴含是指从一个命题（前提）推导出另一个命题（结论）的运算。

蕴含运算的基本规则如下：-公式化：A→B-真假性：当A为真且B为假时，A→B为假；否则为真。

-否定蕴含式：A→B可以等价为¬A∨B-逆蕴含式：A→B可以等价为B→A-传递性：若A→B且B→C，则A→C这些基本运算规则是逻辑代数的基石，通过它们可以进行复杂的逻辑推理和推导。

在实际应用中，逻辑代数的运算规则经常用于电路设计、编程语言的控制流判断、数理逻辑等领域。

逻辑代数的运算规则既具有严密性，又具有普适性，为我们理解和分析复杂命题提供了有效的工具和方法。

一、填空题（每小题△△分，共△△分）（1）逻辑代数中的三种基本的逻辑运算是（与）运算、（或）运算和（非）运算。

（2）逻辑变量和逻辑函数的取值只有（0）和（1）两种取值。

它们表示两种相反的逻辑状态。

（3）与逻辑运算规则可以归纳为有0出（0），全1出（1）。

（4）或逻辑运算规则可以归纳为有1出（1），全0出（0）。

（5）与非逻辑运算规则可以归纳为有（0）出1，全（1）出0。

（6）或非逻辑运算规则可以归纳为有（1）出0，全（0）出1。

（7）二极管从导通到截止所需时间称为（开通）时间。

（8）OC门是集电极（开路）门，使用时必须在电源VCC与输出端之间外接（电阻）。

（9）在数字电路中，三极管工作在（饱和）状态和（截止）状态。

（10）三态输出门输出的三个状态分别为（低电平）、（高电平）、（高阻态）。

（11）逻辑代数中三条重要的规则是（代入）规则、（对偶）规则和（反演）规则。

（12）化简逻辑函数的主要方法有（代数）化简法和（卡诺图）化简法。

（13）逻辑函数的表示方法主要有（函数表达式）、（真值表）、（逻辑）、卡诺图和波形图。

（31）编码器按功能不同分为（二进制）编码器、（二-十进制）编码器和优先编码器。

（32）译码器按功能不同分为（二进制）译码器、（二-十进制）译码器和显示译码器。

（33）8选1数据选择器在所有输入数据都为1时，其输出标准与或表达式共有（ 8 ）个最小项。

（34）输入3位二进制代码的二进制译码器应有（ 8 ）个输出端，共输出（ 8 ）个最小项。

（35）共阳极LED数码管应由输出（低）电平的七段显示译码器来驱动点亮。

而共阴极LED数码管应由输出（高）电平的七段显示译码器来驱动点亮。

（41）二进制数是以（ 2 ）为基数的计数体制，十进制数是以（ 10 ）为基数的计数体制，十六进制是以（ 16 ）为计数体制。

（42）十进制数转换为二进制数的方法是：整数部分用（除2取余），小数部分用（乘2取整）法。

（43）二进制数转换为十进制数的方法是（各位按权展开相加）。

在逻辑代数中，有三种基本逻辑运算，它们分别是：
1. 与运算（AND）：表示两个逻辑命题同时成立的情况。

当且仅当两个命题都为真（True）时，与运算的结果才为真；否则结果为假（False）。

2. 或运算（OR）：表示两个逻辑命题中至少一个成立的情况。

当且仅当至少有一个命题为真时，或运算的结果为真；只有两个命题都为假，结果才为假。

3. 非运算（NOT）：表示对逻辑命题取反的操作。

当一个命题为真时，非运算将其取反为假；当一个命题为假时，非运算将其取反为真。

这三种基本运算在逻辑代数中被用来组合逻辑命题，形成复杂的逻辑表达式。

它们是逻辑计算的基础，常常用于构建逻辑电路、编写计算机程序中的逻辑判断等领域。

逻辑运算在计算机科学、数学、哲学等领域起到了重要的作用。

逻辑运算逻辑代数的基本运算比较简单，只有三种：“与”运算、“或”运算和“非”运算。

任何复杂的逻辑运算都可由这三种基本逻辑运算构成。

如，广泛采用的“与非”、“或非”、“与或非”、“异或” 。

、“同或”等逻辑运算，它们的逻辑关系可以由以上三种基本运算导出。

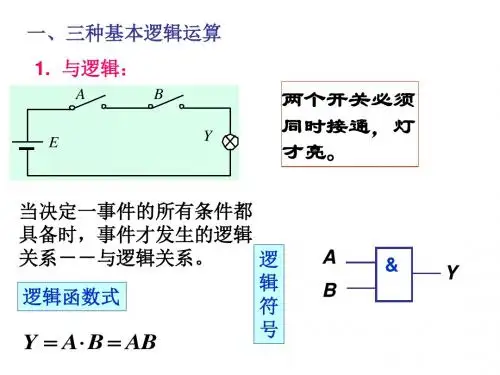
1．“与”运算当决定一事件的所有条件都具备之后，这事件才会发生，称这种因果关系为“与”逻辑关系，或称为“与”逻辑运算或逻辑乘。

条件用逻辑变量“A，B…..”表示，变量取值为1，表示条件具备;取值为0,表示条件不具备。

事件用F表示，只有发生（用1表示）和不发生（用0表示）两种取值。

“与”逻辑运算用表达式表示为：F=A·B 或者F=A ∧B一般简写为：F=AB，把此式称为变量A、B相“与”的逻辑表达式。

用两个串联的开关A、B控制一盏灯，如图1(a)所示。

灯亮的条件是开关A“与”开关B同时处在合上位置。

假定灯亮为“1”，不亮为“0”，开关在合上位置为“1”，在断开位置为“0”，那么，把灯的状态和两个开关所处位置之间的关系列表，如图1(b)所示。

把这种表称为真值表(或称为功能表)。

常用真值表来表示逻辑命题的真假关系。

把所有的条件(输入变量)的全部组合以表格形式列出来，这里为A、B，再把在每一种组合下对应的事件(函数)的值F求出，这张表格就是真值表。

因为每个条件有两种状态“0”、“1”，因此，n个条件就有2n个组合。

图1(b)为A“与”B 的真值表。

同一逻辑函数只可能有唯一的真值表！2．“或”运算当决定事件发生的各种条件中，只要有一个或一个以上条件具备时，这事件就会发生，这样的因果关系称为“或”逻辑关系，或称逻辑加。

“或”运算的逻辑表达式为：F=A+B 或者F=A∨B 。

用并联的两个开关A、B控制一盏灯，如图2(a)所示，只要开关A“或”开关B在合上位置，灯就亮。

按照前面假定来赋值“0”、“1”，列出真值表，如图2(b)所示。

3．“非”运算“非”运算，就是否定，或者称为求反。

逻辑代数逻辑代数（又称布尔代数），它是分析设计逻辑电路的数学工具。

虽然它和普通代数一样也用字母表示变量，但变量的取值只有“0”，“1”两种，分别称为逻辑“0”和逻辑“1”。

这里“0”和“1”并不表示数量的大小，而是表示两种相互对立的逻辑状态。

若定义一种状态为“1”，则另一种状态就为“0”。

例：灯亮用“1”表示、则灯灭就表示为“0”，不考虑灯损坏等其它可能性。

逻辑代数所表示的是逻辑关系（因果关系），而不是数量关系。

这是它与普通代数的本质区别。

1. 基本运算法则一、逻辑代数运算法则从三种基本的逻辑运算关系，我们可以得到以下的基本运算法则（公式1—9）。

0 • 0=01 • 1=10 • 1=0 1 • 0=0公式10 •A=0公式2 1 •A=A 公式3 A •A=A 公式4A •A=0与运算或运算0+0=01+1=10+1=11+0=1公式50 +A=A 公式61+A=1公式7 A +A=A 公式8A+A=1非运算01=10=公式9AA =交换律：结合律：公式11A+B=B+A 公式10A• B=B • A公式13A+(B+C)=(A+B)+C=(A+C)+B 公式12 A• (B • C)=(A • B) • C分配律：公式14A(B+C)=A • B+A • C公式15A+B • C=(A+B)(A+C)（少用）证明：右边=AA+AC+BA+BC=A+AC+BA+BC=A （1+C+B ）+BC=A+BC吸收律：1. 基本运算法则公式16A （A+B ）=A 证明：左边=AA+AB=A+AB=A （1+B ）=A公式17A （A+B ）=AB普通代数不适用！证明：BA B A A A B A A +=++=+)15())((公式DCBC A DC BC A A ++=++被吸收B A B A A +=+公式19（常用）公式18A+AB=A （常用）证明：A+AB=A(1+B)=A•1=A CDAB )F E (D AB CD AB +=+++1. 基本运算法则例：例：1. 基本运算法则公式20AB+AB=A公式21（A+B ）（A+B ）=A（少用）证明：BC)A A (C A AB BCC A AB +++=++CA AB BC A C AB BC A ABC C A AB +=+++=+++=)1()1(推论：CA AB BCDC A AB +=++1C A AB BC C A AB +=++公式22（常用）摩根定律公式23B A AB +=（常用）公式24BA B A ∙=+（常用）记忆：记忆：可以用列真值表的方法证明：A B 00110011A B 00001111AB A+B 00111111A+B A• B 00000011公式25=⊕B A AB或A B =BA ⊕其中：BA B A B A +=⊕是异或函数BA AB B A+=是同或函数用列真值表的方法证明：A B 00110011ABAB10000100B A 11000000A B 1100B A ⊕0011A B其中，吸收律公式16 A （A+B ）= A 公式18 A+AB = A对偶式BA B A A +=+公式19公式20AB+AB=A 公式21(A+B)(A+B)=A对偶关系：将某逻辑表达式中的与（• ）换成或（+），或（+）换成与（• ），得到一个新的逻辑表达式，即为原逻辑式的对偶式。