逻辑代数中的三种基本运算分解

逻辑代数的三个基本运算逻辑代数是一种数学分支，研究命题和命题之间的逻辑关系。

它主要包括命题逻辑和谓词逻辑两个部分。

在逻辑代数中，有三个基本运算，即合取、析取和否定。

接下来，我将一步一步回答有关逻辑代数的这三个基本运算的问题。

一、合取运算（AND）合取运算，也称为与运算，用∧（圆圈上有一个小竖杠）表示。

在逻辑代数中，合取运算指的是将两个或多个命题连接起来，当且仅当这些命题都为真时，合取命题才为真。

1. 合取命题的真值表首先，我们可以通过真值表来表示合取命题。

假设有两个命题P和Q，可以通过以下真值表来表示合取命题：P Q P∧QT T TT F FF T FF F F从上表可以看出，当且仅当P和Q的值均为真时，合取命题才为真。

2. 合取的代数表达式除了使用真值表，我们还可以使用代数表达式来表示合取命题。

例如，我们可以用“P ∧Q”来表示“P和Q的合取”。

在逻辑代数中，合取的代数表达式遵循以下规则：- 合取满足交换律：P ∧Q = Q ∧P- 合取满足结合律：(P ∧Q) ∧R = P ∧(Q ∧R)- 合取满足吸收律：P ∧(P ∨Q) = P二、析取运算（OR）析取运算，也称为或运算，用∨（有一个小竖杠在圆圈顶部）表示。

在逻辑代数中，析取运算是将两个或多个命题连接起来，当且仅当这些命题中至少有一个为真时，析取命题才为真。

1. 析取命题的真值表与合取运算类似，我们可以使用真值表来表示析取命题。

假设有两个命题P和Q，可以通过以下真值表来表示析取命题：P Q P∨QT T TT F TF T TF F F从上表可以看出，只有当P和Q的值至少有一个为真时，析取命题才为真。

2. 析取的代数表达式类似于合取运算，我们可以使用代数表达式来表示析取命题。

例如，我们可以用“P ∨Q”来表示“P或Q的析取”。

在逻辑代数中，析取的代数表达式遵循以下规则：- 析取满足交换律：P ∨Q = Q ∨P- 析取满足结合律：(P ∨Q) ∨R = P ∨(Q ∨R)- 析取满足分配律：P ∨(Q ∧R) = (P ∨Q) ∧(P ∨R)三、否定运算（NOT）否定运算，也称为非运算，用¬表示。

《数字电子技术基础》读书笔记02 逻辑代数基础2.1从布尔代数到逻辑代数1849年英国数学家乔治布尔(George Boole)提出布尔代数，使用数学方法进行逻辑运算。

把布尔代数应用到二值逻辑电路中，即为逻辑代数。

2.2逻辑代数中的运算(想想初等代数中的加减乘除)2.2.1三种基本运算与(AND)：逻辑乘，Y=A B或(OR)：逻辑加，Y=A+B非(NOT)：逻辑求反，Y=Aˊ简单逻辑运算(与、或、非)的两套图形符号，均为IEEE(国际电气与电子工程师协会)和IEC(国际电工协会)认定。

上排为国外教材和EDA软件中普遍使用的特定外形符号；下排为矩形符号。

2.2.2复合逻辑运算(都可以表示为与、或、非的组合)与非(NAND)：先与后非，与的反运算，Y=(A B)ˊ或非(NOR)：先或后非，非的反运算，Y=(A+B)ˊ与或非(AND-NOR)：先与再或再非，Y=(A B+C D)ˊ异或(Exclusive OR)：Y=A⊕B=A Bˊ+AˊB A和B不同，Y为1；A和B相同，Y为0。

当A与B相反时，A Bˊ和AˊB，肯定有一个结果为1，则Y为1。

同或(Exclusive NOR)：Y=A⊙B=A B+AˊBˊA和B相同，Y为1；A和B不同，Y为0。

当A与B相同时，A B和AˊBˊ，肯定有一个结果为1，则Y为1。

同或与同或互为反运算，即两组运算，只要输入相同，一定结果相反。

A⊕B=(A⊙B)ˊA⊙B=(A⊕B)ˊ复合逻辑运算的图像符号和运算符号。

2.3逻辑代数的基本公式和常用公式2.3.1基本公式(见对偶定理)2.3.2若干常用公式(见逻辑函数化简方法之公式化简法)2.4逻辑代数的基本定理2.4.1代入定理(相当于初等代数中的换元)任何一个包含逻辑变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，则等式依然成立。

2.4.2反演定理对于任意一个逻辑式Y，若将其中所有的""换成"+"，"+"换成""，"0"换成"1"，"1"换成"0"，原变量换成反变量，反变量换成原变量，则得到的结果就是Yˊ。

逻辑代数的基本运算法则
逻辑代数是描述、分析和简化逻辑线路的有效的数学工具，它又称为开关代数或布尔代数。

逻辑代数的变量（简称逻辑变量）的取值范围只有“0”或“1”。

“0”与“1”不表示数量的多少，而是表示具体问题的两种可能。

例如，用“0”与“1”代表开关线路中开关的断开和接通，电压的低和高，晶体管的截止和导通，信号的无和有两种物理状态。

一个复杂的开关线路总是由若干个开关元件组成。

这种相互联系的关系反映到数学上就是几种逻辑运算。

逻辑加、逻辑乘和逻辑非。

这三种逻辑运算反映了实际中开关元件之间最基本的联系。

(1)逻辑加（“或”运算），或门对应的逻辑运算是“逻辑加”C=A+B。

(2)逻辑乘（“与”运算），与门对应的逻辑运算是“逻辑乘”C=A ×B。

(3)逻辑非（“非”运算），“逻辑非”运算和非门相对应，记为B=。

第2章逻辑代数基础2.1 概述一、算术运算和逻辑运算在数字电路中,二进制数码不仅可以表示数值的大小，而且可以表示事物的状态,当两个二进制数码表示两个数值大小时，它们之间可进行数值运算，即算术运算。

当两个二进制数码表示不同逻辑状态时，它们之间的因果关系可进行逻辑运算。

算术运算与逻辑运算有本质的差别,下面重点介绍逻辑运算的各种规则。

二、几个基本概念1、逻辑状态表示法一种状态高电位有真是美生 1 0另一种状态低电位无假非丑死 0 12、两种逻辑体制1 高电位低电位0 低电位高电位正逻辑负逻辑3、高低电平的规定正逻辑负逻辑2.2 逻辑代数中的三种基本运算1、与逻辑（与运算）(逻辑乘)与逻辑的定义：仅当决定事件（Y）发生的所有条件（A，B，C，…）均满足时，事件（Y）才能发生。

表达式为：Ｙ＝ＡＢＣ开关A，B串联控制灯泡Y2、或逻辑（或运算）或逻辑的定义：当决定事件（Y ）发生的各种条件（A ，B ，C ，…)中，只要有一个或多个条件具备，事件（Y ）就发生。

表达式为：Ｙ＝Ａ＋Ｂ＋Ｃ＋…开关A ，B 并联控制灯泡YA 、B 都断开，灯不亮。

A 断开、B 接通，灯亮。

A 接通、B 断开，灯亮。

A 、B 都接通，灯亮。

两个开关只要有一个接通，灯就会亮。

逻辑表达式为：Ｙ＝Ａ+Ｂ功能表3（A ）满足时，开关A 控制灯泡YA 断开，灯亮。

A 接通，灯灭。

功 能 表Ｙ＝Ａ4（（（（1、代入定理：任何一个含有变量A A的位置都用同一个逻辑函数代替，则等式仍然成立。

这个规则称为代入定理。

例如，已知等式，用函数Y=AC代替等式中的A，根据代入规则，等式仍然成立，即有：（2）反演定理：对于任何一个逻辑表达式Y，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，那么所得到的表达式就是函数Y的反函数Y（或称补函数）。

这个规则称为反演定理。

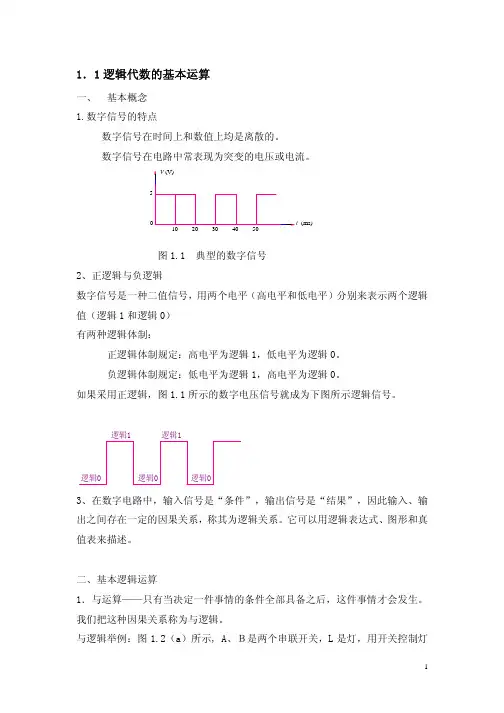
1．1逻辑代数的基本运算一、 基本概念 1.数字信号的特点数字信号在时间上和数值上均是离散的。

数字信号在电路中常表现为突变的电压或电流。

图1.1 典型的数字信号2、正逻辑与负逻辑数字信号是一种二值信号，用两个电平（高电平和低电平）分别来表示两个逻辑值（逻辑1和逻辑0） 有两种逻辑体制：正逻辑体制规定：高电平为逻辑1，低电平为逻辑0。

负逻辑体制规定：低电平为逻辑1，高电平为逻辑0。

如果采用正逻辑，图1.1所示的数字电压信号就成为下图所示逻辑信号。

3、在数字电路中，输入信号是“条件”，输出信号是“结果”，因此输入、输出之间存在一定的因果关系，称其为逻辑关系。

它可以用逻辑表达式、图形和真值表来描述。

二、基本逻辑运算1．与运算——只有当决定一件事情的条件全部具备之后，这件事情才会发生。

我们把这种因果关系称为与逻辑。

与逻辑举例：图1.2（a）所示, A、Ｂ是两个串联开关，L 是灯，用开关控制灯逻辑0逻辑1逻辑0逻辑1逻辑0V t (V)(ms)51020304050亮和灭的关系如图2（b）所示。

设1表示开关闭合或灯亮；0表示开关不闭合或灯不亮，则得真值表图2（c）所示V(c)图1.2与逻辑运算（a）电路图（b）真值表（c）逻辑真值表（d）逻辑符若用逻辑表达式来描述，则可写为与运算的规则为： “输入有0，输出为0；输入全1，输出为1”。

数字电路中能实现与运算的电路称为与门电路，其逻辑符号如图（d）所示。

与运算可以推广到多变量：⋅⋅⋅=C B A L ……2．或运算——当决定一件事情的几个条件中，只要有一个或一个以上条件具备，这件事情就发生。

我们把这种因果关系称为或逻辑。

或逻辑举例：如图1.3（a）所示，或运算的真值表如图1.3（b ）所示，逻辑真值表如图1.3（c ）所示。

若用逻辑表达式来描述，则可写为L ＝A+B或运算的规则为：“输入有1，输出为1；输入全0，输出为0”。

BA L ⋅=(c)图1.3或逻辑运算（a） 电路图（b）真值表（c）逻辑真值表（d）逻辑符号在数字电路中能实现或运算的电路称为或门电路，其逻辑符号如图（d）所示。

一.逻辑运算当二进制代码表示不同的逻辑状态时，可以按照一定的规则进行推理运算1.三种基本的逻辑关系①与②或③非④几种常用的复合逻辑运算2.逻辑代数的基本公式和常用公式①基本公式①基本公式3.逻辑代数的基本定理①代入定理：在任何一个包含A的逻辑式中，若以另外一个逻辑式代入式子中A的位置，则等式依然成立②反演定理：如果一个表达式想要取反，那么就在这个表达式中将原变量变为反变量，将反变量变为原变量即可。

4.逻辑函数及其表示方法如果以逻辑变量为输入，运算结果为输出，则输入变量的值确定以后，输出的取值也会随之而定。

输入输出之间是一种函数关系注：在二值逻辑中，输入输出都只有两种取值可能，非零即一。

1.逻辑函数的两种标准表达形式①最小项之和：最小项M，其中M是乘积项，它包含N个因子，N个变量均以原变量和反变量的形式在M中出现一次最小项的编号：最小项的性质：在输入变量任意一个取值下，有且仅有一个最小项的值为1.全体最小项之和为1.任何两个最小项之积为0两个相邻的最小项之和可以合并，消掉一对因子，只留下一个公共因子。

注：相邻指的仅一个变量不同的两项。

②最大项之积最大项：M是相加项，它包含了N个因子，N个变量均以原变量或者反变量的形式在M中出现一次。

其实最小项与最大项是可以相互进行转变的，转变的方式就是摩根定理。

5.逻辑函数的化简逻辑函数的最简形式：最简与或包含的乘积项已经最少，每个乘积项的因子也最少称为最简的与或逻辑式。

①卡诺图化简法：实质：将逻辑函数的最小项之和以图形的方式表达出来以2的N次方分别代表N变量的所有最小项，并且将他们排列成矩阵，而且使得几何位置相邻的两个最小项在逻辑上也是相邻的（只有一个变量不同），这样就得到表示N变量全部最小项的卡诺图。

用卡诺图化简函数：依据：具有相邻的最小项可以合并，消去不同的因子，并且在卡诺图中，最小项的相邻可以直观的从图中反映出来。

合并最小项的原则：两个相邻的最小项可以合并成一项，消去一对因子；四个排成矩形的相邻最小项可以合并成一项，消去两对因子；八个相邻的最小项可以合并为一项，消去三对因子；。

电子技术基础知识1、逻辑代数的基本运算有与、或、非三种。

2、只有决定事物结果的全部条件同时具备时，结果才发生。

这种因果关系称为逻辑与，或称逻辑相乘。

3、在决定事物结果的诸条件中只要有任何一个满足，结果就会发生。

这种因果关系称为逻辑或，也称逻辑相加。

4、只要条件具备了，结果便不会发生；而条件不具备时，结果一定发生。

这种因果关系称为逻辑非，也称逻辑求反。

5、逻辑代数的基本运算有重叠律、互补律、结合律、分配律、反演律、还原律等。

举例说明。

6、对偶表达式的书写。

7、逻辑该函数的表示方法有：真值表、逻辑函数式、逻辑图、波形图、卡诺图、硬件描述语言等。

8、在n变量逻辑函数中，若m为包含n个因子的乘积项，而且这n个变量均以原变量或反变量的形式在m中出现一次，则称m为该组变量的最小项。

9、n变量的最小项应有2n个。

10、最小项的重要性质有：①在输入变量的任何取值下必有一个最小项，而且仅有一个最小项的值为1；②全体最小项之和为1；③任意两个最小项的乘积为0；④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。

11、若两个最小项只有一个因子不同，则称这两个最小项具有相邻性。

12、逻辑函数形式之间的变换。

（与或式—与非式—或非式--与或非式等）13、化简逻辑函数常用的方法有：公式化简法、卡诺图化简法、Q-M法等。

14、公式化简法经常使用的方法有：并项法、吸收法、消项法、消因子法、配项法等。

15、卡诺图化简法的步骤有：①将函数化为最小项之和的形式；②画出表示该逻辑函数的卡诺图；③找出可以合并的最小项；④选取化简后的乘积项。

16、卡诺图法化简逻辑函数选取化简后的乘积项的选取原则是：①乘积项应包含函数式中所有的最小项；②所用的乘积项数目最少；③每个乘积项包含的因子最少。

手把手教你写程序：内容：从最简单的程序入手，手把手教你写程序，让同学们拿到一个复杂的程序或者任务，能快速找到切入点，写出程序，再在此基础上优化程序。

当拿到一个单片机任务时，不要急于动手写程序，先仔细分析它的以下几个点：1、它要单片机整体实现什么功能2、功能细分（模块化），先干什么，再干什么，最后干什么3、画初步流程图，（把几个模块画出即可）4、模块之间的分析：一个模块到另一个模块之间，怎么变换，怎么连接（优化流程图）5、单个模块分析：每个模块要做什么（流程图细化）6、所有模块结合连接，细化所有流程图7、分析单个模块每步要用到的方法或者指令8、总流程图定型9、纸上写程序，对照流程图分析其可行性，若不可行则返回10、上机调试，加注释以上十步，缺一不可（小程序列外）切记：流程图的确定很重要，需反复修改大忌：拿到任务，不仔细分析就写程序。

数字电路-逻辑代数基础逻辑代数基础逻辑代数中的三种基本运算与、或、⾮复合逻辑运算最常见的有与⾮、或⾮、与或⾮、异或、同或等。

异或：A⨁B=AB′+A′B同或：A⨀B=AB+A′B′异或与同或互为反运算。

逻辑代数的基本公式和常⽤公式基本公式也叫布尔恒等式（证明⽅法包括真值表法和推演法）：总结为以下⼏类：开始为0⾏1. 变量与常量间的运算规则：1、2⾏2. 重叠律（同⼀变量）：3⾏3. 互补律（变量和其反变量）：4⾏4. 交换律（5⾏）结合律（6⾏）分配律（7⾏）5. De.Morgan定理，反演律（8⾏）6. 还原律：（9）若⼲常⽤公式由基本公式导出，便于化简逻辑函数。

1. 两个乘积项相加时，若⼀项以另⼀项为因⼦，则该项多余：A+AB=A2. 两个乘积项相加时，⼀项取反后是另⼀项的因⼦，则此因⼦多余，可以消去：A+A′B=A+B3. 两个乘积项相加时，若他们分别包含B和B′两个因⼦⽽其他因⼦相同，则两项可合并。

AB+AB′=A4. 变量A和包含A的和相乘时，结果为A:A(A+B)=A5. 若两个乘积项中分别包含A和A′两个因⼦，则其余因⼦组成第三个乘积项时，第三个乘积项是多余的：AB+A′C+BC=AB+A′C进⼀步AB+A′C+BCD=AB+A′C6. A和⼀个乘积项的⾮相乘，且A为这个乘积项的因⼦时，A这个因⼦可以消去：A(AB)′=AB′7. A′和⼀个乘积项的⾮相乘，且A为这个乘积项的因⼦时，结果等于A′A′(AB)′=A′逻辑代数的基本定理代⼊定理在任何⼀个包含A的逻辑等式中，若以另外⼀个逻辑式代⼊式中所有A的位置，则等式依然成⽴。

反演定理对于任意⼀个逻辑式Y,若将其中所有的“⋅”换成“+”,“+”换成“⋅”,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到的结果就是Y′。

这个规律称为反演定理。

反演定理为求取已知逻辑式的反逻辑式提供了⽅便。

在使⽤反演定理时,还需注意遵守以下两个规则:①仍需遵守“先括号、然后乘、最后加”的运算优先次序。

逻辑代数逻辑代数（又称布尔代数），它是分析设计逻辑电路的数学工具。

虽然它和普通代数一样也用字母表示变量，但变量的取值只有“0”，“1”两种，分别称为逻辑“0”和逻辑“1”。

这里“0”和“1”并不表示数量的大小，而是表示两种相互对立的逻辑状态。

若定义一种状态为“1”，则另一种状态就为“0”。

例：灯亮用“1”表示、则灯灭就表示为“0”，不考虑灯损坏等其它可能性。

逻辑代数所表示的是逻辑关系（因果关系），而不是数量关系。

这是它与普通代数的本质区别。

1. 基本运算法则一、逻辑代数运算法则从三种基本的逻辑运算关系，我们可以得到以下的基本运算法则（公式1—9）。

0 • 0=01 • 1=10 • 1=0 1 • 0=0公式10 •A=0公式2 1 •A=A 公式3 A •A=A 公式4A •A=0与运算或运算0+0=01+1=10+1=11+0=1公式50 +A=A 公式61+A=1公式7 A +A=A 公式8A+A=1非运算01=10=公式9AA =交换律：结合律：公式11A+B=B+A 公式10A• B=B • A公式13A+(B+C)=(A+B)+C=(A+C)+B 公式12 A• (B • C)=(A • B) • C分配律：公式14A(B+C)=A • B+A • C公式15A+B • C=(A+B)(A+C)（少用）证明：右边=AA+AC+BA+BC=A+AC+BA+BC=A （1+C+B ）+BC=A+BC吸收律：1. 基本运算法则公式16A （A+B ）=A 证明：左边=AA+AB=A+AB=A （1+B ）=A公式17A （A+B ）=AB普通代数不适用！证明：BA B A A A B A A +=++=+)15())((公式DCBC A DC BC A A ++=++被吸收B A B A A +=+公式19（常用）公式18A+AB=A （常用）证明：A+AB=A(1+B)=A•1=A CDAB )F E (D AB CD AB +=+++1. 基本运算法则例：例：1. 基本运算法则公式20AB+AB=A公式21（A+B ）（A+B ）=A（少用）证明：BC)A A (C A AB BCC A AB +++=++CA AB BC A C AB BC A ABC C A AB +=+++=+++=)1()1(推论：CA AB BCDC A AB +=++1C A AB BC C A AB +=++公式22（常用）摩根定律公式23B A AB +=（常用）公式24BA B A ∙=+（常用）记忆：记忆：可以用列真值表的方法证明：A B 00110011A B 00001111AB A+B 00111111A+B A• B 00000011公式25=⊕B A AB或A B =BA ⊕其中：BA B A B A +=⊕是异或函数BA AB B A+=是同或函数用列真值表的方法证明：A B 00110011ABAB10000100B A 11000000A B 1100B A ⊕0011A B其中，吸收律公式16 A （A+B ）= A 公式18 A+AB = A对偶式BA B A A +=+公式19公式20AB+AB=A 公式21(A+B)(A+B)=A对偶关系：将某逻辑表达式中的与（• ）换成或（+），或（+）换成与（• ），得到一个新的逻辑表达式，即为原逻辑式的对偶式。