逻辑代数的基本公式和运算规则

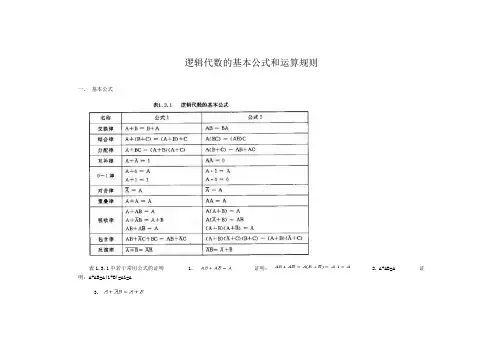
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1．证明： 2. A+AB=A 证明：A+AB=A(1+B)=A1=A
3.
证明：
4.
证明：
推论：
二、运算规则
1．代入定理任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立，这称为代入规则。

利用代入规则，反演律能推广到n个变量，即:
2．反演定理对于任意一个逻辑函数式F，若把式中的运算符“.”换成“+”, “+” 换成“.”，常量“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，则得到的结果为。

这个规则叫反演定理运用反演定理时注意两点：① 必须保持原函数的运算次序。

② 不属于单个变量上的非号保留，而非号下面的函数式按反演规则变换。

例如：
其反函数：
3．对偶定理对于任意一个逻辑函数F，若把式中的运算符“.”换成“+”，“+”换成“.”，常量“0”换成“1”，“1”换成“0”，则得到F的对偶式F′。

例如：
其对偶式：
对偶定理：如果两个函数式相等，则它们对应的对偶式也相等。

逻辑代数的运算法则逻辑代数又称布尔代数。

逻辑代数与普通代数有着不同概念，逻辑代数表示的不是数的大小之间的关系，而是逻辑的关系，它仅有0、1两种状态。

逻辑代数有哪些基本公式和常用公式呢？1.变量与常量的关系与运算公式 一、基本公式A·1=AA·0=0或运算公式A+0=A A+1=101律2.与普通代数相似的定律与运算公式A·B=B·A 或运算公式A+B=B+A交换律A·(B·C)=(A·B)·C A+(B+C)=(A+B)+C 结合律A·(B+C)=A·B+A·C A+(B·C)=(A+B)(A+C)分配律3.逻辑代数特有的定律与运算公式或运算公式互补律重叠律（同一律） 反演律（摩根定律）0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+ 非非律（还原律）AA =A A A =⋅A A A =+真值表证明摩根定律0001101111111100结论：BA B A +=⋅ 以上定律的证明，最直接的办法就是通过真值表证明。

若等式两边逻辑函数的真值表相同，则等式成立。

【证明】公式1AB A AB =+B A AB +）（B B A += 互补律1⋅=A 01律A= 合并互为反变量的因子【证明】公式2AAB A =+AB A +）（B A +=1 01律A= 吸收多余项【证明】公式3BA B A A +=+B A A +BA AB A ++=B A A A ）（++= 互补律BA += 消去含有另一项的反变量的因子【证明】CA AB BC C A AB +=++BC A A C A AB ）（+++=BC C A AB ++ 分配律BC A ABC C A AB +++= 吸收多余项公式2互补律CA AB += 公式2逻辑代数的运算法则一、基本公式二、常用公式A·1=AA·0=0A+0=A A+1=1 1.变量与常量的关系01律2.与普通代数相似的定律交换律A·B=B·A A+B=B+A结合律 分配律3.逻辑代数特有的定律互补律A·A=A A+A=A 重叠律（同一律）反演律（摩根定律）0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+非非律（还原律）AA =AB A AB =+.1AAB A =+.2BA B A A +=+.3CA AB BC C A AB +=++.4A·(B·C )=(A·B )·C A+(B+C )=(A+B )+C A·(B+C )=A·B+A·CA +(B·C )=(A+B )(A+C )谢谢！。

逻辑代数的基本公式和
运算规则
-CAL-FENGHAI.-(YICAI)-Company One1
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1．证明： 2. A+AB=A 证明：A+AB=A(1+B)=A1=A
3.
2
证明：
4.
证明：
推论：
二、运算规则1．代入定理任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立，这称为代入规则。

利用代入规则，反演律能推广到n个变量，即:
2．反演定理对于任意一个逻辑函数式F，若把式中的运算符“.”换成“+”, “+” 换成“.”，常量“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，则得到的结果为。

这个规则叫反演定理运用反演定理时注意两点：① 必须保持原函数的运算次序。

② 不属于单个变量上的非号保留，而非号下面的函数式按反演规则变换。

例如：
其反函
数：
3．对偶定理对于任意一个逻辑函数F，若把式中的运算符“.”换成“+”，“+”换成“.”，常量“0”换成“1”，“1”换成“0”，则得到F的对偶式F′。

例如：
3
其对偶
式：
对偶定理：如果两个函数式相等，则它们对应的对偶式也相等。

4。

逻辑代数的基本公式、定律和规则示例文章篇一：《逻辑代数的基本公式、定律和规则》一、逻辑代数的基本公式1. 常量之间的运算公式- 0和1是逻辑代数中的两个常量。

0就像是黑暗，1就像是光明。

在逻辑代数里，0 + 0 = 0，这就好比两个黑暗加在一起还是黑暗呀。

那0 + 1 = 1呢，就好像黑暗里来了一点光明，那结果就是光明啦。

1 + 1 = 1，这可能有点奇怪，可这就像两个光明加在一起还是光明，不会变得更亮啦。

- 0×0 = 0，这很好理解，就像两个没有东西相乘还是没有东西。

0×1 = 0，就像没有东西和有东西相乘，结果就是没有东西。

1×1 = 1，有东西和有东西相乘还是有东西嘛。

2. 变量与常量的运算公式- 对于变量A，A + 0 = A。

这就像你有一个东西A，再加上没有东西（0），那还是你原来的东西A呀。

A + 1 = 1，不管你原来有什么东西A，再加上光明（1），那结果就是光明（1）啦。

- A×0 = 0，不管你是什么东西A，和没有东西（0）相乘，结果就是没有东西（0）。

A×1 = A，就像你有东西A，和有东西（1）相乘，结果还是你原来的东西A。

3. 同一律、互补律等公式- 同一律就是A×A = A，A + A = A。

比如说你有一个苹果A，那一个苹果乘以一个苹果还是一个苹果，一个苹果加上一个苹果还是一个苹果（在逻辑代数的概念里哦）。

- 互补律是A×A' = 0，A+A' = 1。

A'就像是A的反面。

如果A是白天，A'就是黑夜。

白天和黑夜不能同时存在（A×A' = 0），而白天或者黑夜肯定有一个存在（A+A' = 1）。

二、逻辑代数的基本定律1. 交换律- 在逻辑代数里，加法交换律是A + B = B + A，就像你有苹果A和香蕉B，先数苹果再数香蕉，和先数香蕉再数苹果，总数是一样的。

一.逻辑运算当二进制代码表示不同的逻辑状态时，可以按照一定的规则进行推理运算1.三种基本的逻辑关系①与②或③非④几种常用的复合逻辑运算2.逻辑代数的基本公式和常用公式①基本公式①基本公式3.逻辑代数的基本定理①代入定理：在任何一个包含A的逻辑式中，若以另外一个逻辑式代入式子中A的位置，则等式依然成立②反演定理：如果一个表达式想要取反，那么就在这个表达式中将原变量变为反变量，将反变量变为原变量即可。

4.逻辑函数及其表示方法如果以逻辑变量为输入，运算结果为输出，则输入变量的值确定以后，输出的取值也会随之而定。

输入输出之间是一种函数关系注：在二值逻辑中，输入输出都只有两种取值可能，非零即一。

1.逻辑函数的两种标准表达形式①最小项之和：最小项M，其中M是乘积项，它包含N个因子，N个变量均以原变量和反变量的形式在M中出现一次最小项的编号：最小项的性质：在输入变量任意一个取值下，有且仅有一个最小项的值为1.全体最小项之和为1.任何两个最小项之积为0两个相邻的最小项之和可以合并，消掉一对因子，只留下一个公共因子。

注：相邻指的仅一个变量不同的两项。

②最大项之积最大项：M是相加项，它包含了N个因子，N个变量均以原变量或者反变量的形式在M中出现一次。

其实最小项与最大项是可以相互进行转变的，转变的方式就是摩根定理。

5.逻辑函数的化简逻辑函数的最简形式：最简与或包含的乘积项已经最少，每个乘积项的因子也最少称为最简的与或逻辑式。

①卡诺图化简法：实质：将逻辑函数的最小项之和以图形的方式表达出来以2的N次方分别代表N变量的所有最小项，并且将他们排列成矩阵，而且使得几何位置相邻的两个最小项在逻辑上也是相邻的（只有一个变量不同），这样就得到表示N变量全部最小项的卡诺图。

用卡诺图化简函数：依据：具有相邻的最小项可以合并，消去不同的因子，并且在卡诺图中，最小项的相邻可以直观的从图中反映出来。

合并最小项的原则：两个相邻的最小项可以合并成一项，消去一对因子；四个排成矩形的相邻最小项可以合并成一项，消去两对因子；八个相邻的最小项可以合并为一项，消去三对因子；。