第7章弯曲正应力(1,2)

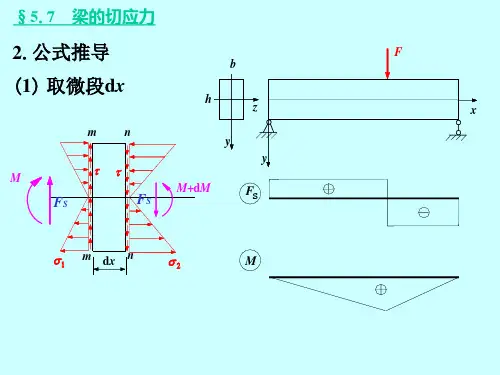
第7章弯曲应力引言前一章讨论了梁在弯曲时的内力——剪力和弯矩。

但是，要解决梁的弯曲强度问题，只了解梁的内力是不够的，还必须研究梁的弯曲应力，应该知道梁在弯曲时，横截面上有什么应力，如何计算各点的应力。

在一般情况下，横截面上有两种内力——剪力和弯矩。

由于剪力是横截面上切向内力系的合力，所以它必然与切应力有关；而弯矩是横截面上法向内力系的合力偶矩，F时，就必然有切应力τ；所以它必然与正应力有关。

由此可见，梁横截面上有剪力Q有弯矩M时，就必然有正应力 。

为了解决梁的强度问题，本章将分别研究正应力与切应力的计算。

弯曲正应力纯弯曲梁的正应力由前节知道，正应力只与横截面上的弯矩有关，而与剪力无关。

因此，以横截面上只有弯矩，而无剪力作用的弯曲情况来讨论弯曲正应力问题。

在梁的各横截面上只有弯矩，而剪力为零的弯曲，称为纯弯曲。

如果在梁的各横截面上，同时存在着剪力和弯矩两种内力，这种弯曲称为横力弯曲或剪切弯曲。

例如在图7-1所示的简支梁中，BC段为纯弯曲，AB段和CD段为横力弯曲。

分析纯弯曲梁横截面上正应力的方法、步骤与分析圆轴扭转时横截面上切应力一样，需要综合考虑问题的变形方面、物理方面和静力学方面。

图7-1变形方面为了研究与横截面上正应力相应的纵向线应变，首先观察梁在纯弯曲时的变形现象。

为此，取一根具有纵向对称面的等直梁，例如图7-2(a)所示的矩形截面梁，并在梁的侧面上画出垂直于轴线的横向线m-m、n-n和平行于轴线的纵向线d-d、b -b 。

然后在梁的两端加一对大小相等、方向相反的力偶e M ，使梁产生纯弯曲。

此时可以观察到如下的变形现象。

纵向线弯曲后变成了弧线''a a 、''b b , 靠顶面的aa 线缩短了，靠底面的bb 线伸长了。

横向线m -m 、n -n 在梁变形后仍为直线，但相对转过了一定的角度，且仍与弯曲了的纵向线保持正交，如图7-2(b)所示。

梁内部的变形情况无法直接观察，但根据梁表面的变形现象对梁内部的变形进行如下假设：(1) 平面假设 梁所有的横截面变形后仍为平面．且仍垂直于变形后的梁的轴线。

工程力学（第2版）第7章 弯 曲题 库： 主观题7-1 长度为250mm ，截面尺寸为0.8mm 25mm h b ⨯=⨯的薄钢板卷尺，由于两端外力偶的作用而弯成中心角为030的圆弧。

已知弹性模量52.110MPa E =⨯。

试求钢尺横截面上的最大正应力。

解：由题知302250mm 360πρ⋅= ，故480mm ρ= 卷尺最外层纤维应变最大，且为4max 0.428.3310480hερ-===⨯ 由拉压胡克定律可知 54max max 2.1108.3310176MPa E σε-==⨯⨯⨯=即钢尺横截面上的最大正应221(0.250.23)760.573kN /m 4q π=-⨯=力为176MPa .知识点：1．梁横截面的应力。

参考页: P145。

学习目标: 2（掌握梁横截面上的应力计算方法，会利用应力计算公式计算正应力） 难度: 1.0提示一：该题考察知识点：1. 梁横截面上的应力计算。

提示二：无 提示三：无 提示四（同题解） 题解：1、利用正应力计算公式计算正应力。

7-2 一外径为250mm ，壁厚为10mm ，长度l=12m 的铸铁水管，两端搁在支座上，管中充满着水，如图所示。

铸铁的容量3176kN /m γ=，水的容重3210kN /m γ=。

试求管内最大拉、压正应力的数值。

解：每米铸铁水管的重量 每米水柱的重量22220.2310.231100.415kN /m 44q y ππ=⨯⨯⨯=⨯⨯⨯=故水管所受均布荷载120.988kN /m q q q =+=在水管中部有弯矩最大值22max 110.9881217.784kN m 88M ql ==⨯⨯=⋅最大弯曲正应力为3max max343217.7841040.7MPa 2300.25[1()]250z M W σπ⨯⨯===⨯⨯-故管内最大拉、压正应力的数值为,max ,max 40.7MPa t c σσ==。

知识点：1．梁横截面的应力。

43 第7章弯曲强度7－1 直径为d 地圆截面梁,两端在对称面内承受力偶矩为M 地力偶作用,如图所示.若已知变形后中性层地曲率半径为ρ；材料地弹性模量为E .根据d 、ρ、E 可以求得梁所承受地力偶矩M .现在有4种答案,请判断哪一种是正确地.(A)M ＝E π d 习题7－1图(B) 64ρ M ＝64ρ (C) E π d4M ＝E π d (D)32ρM ＝32ρ E π d 3正确答案是A .7－2关于平面弯曲正应力公式地应用条件,有以下4种答案,请判断哪一种是正确地.(A)细长梁、弹性范围内加载；(B)弹性范围内加载、载荷加在对称面或主轴平面内；(C)细长梁、弹性范围内加载、载荷加在对称面或主轴平面内； (D)细长梁、载荷加在对称面或主轴平面内.正确答案是C _.7－3长度相同、承受同样地均布载荷q 作用地梁,有图中所示地4种支承方式,考虑,请判断哪一种支承方式最合理.l 5习题7－3图d . 7－4悬臂梁受力及截面尺寸如图所示.图中地尺寸单位为mm .求：梁地1－1截面上A 、−⎜ ⎟ A z B 两点地正应力.习题7－4图解：1. 计算梁地1－1截面上地弯矩：M =⎛1×103N ×1m+600N/m ×1m ×1m ⎞=−1300N ⋅m⎝2 ⎠2. 确定梁地1－1截面上A 、B 两点地正应力： A 点：⎛150×10−3m ⎞ 1300N ⋅m ×⎜−20×10−3m ⎟σ =M z y =⎝2⎠＝2.54×106Pa =2.54MPa(拉应力) I zB 点：100×10-3m ×(150×10-3m )3121300N ⋅m ×⎜0.150m−0.04m ⎟⎛⎞σ=M z y =⎝2⎠=1.62×106Pa =1.62MPa(压应力)B 0.1m×(0.15m )3 127－5 简支梁如图所示.试求I-I 截面上A 、B 两点处地正应力,并画出该截面上地正应力 分布图. 习题7－5图A (a)A C B(b)F R AkN ⋅解：（1）求支座约束力F RA =3.64kN,F RB =4.36kN习题7－5解图（2）求I －I 截面地弯矩值（见习题7－5解图b ）M I −I =3.64kN ⋅m（3）求所求点正应力σ=M I-I y AI z33I =bh 12=75×150 12=21.1×106mm 4 y A =(75−40)=35mm6∴σ=−3.64×10 ×35=−6.04MPa A 21.1×1066σ=3.64×10 ×75=12.94MPa B 21.1×1067－6加热炉炉前机械操作装置如图所示,图中地尺寸单位为mm .其操作臂由两根无缝 钢管所组成.外伸端装有夹具,夹具与所夹持钢料地总重F P ＝2200N ,平均分配到两根钢管上.求：梁内最大正应力（不考虑钢管自重）.3习题7－6图解：1．计算最大弯矩：−33M max =−2200N ×2395×10m=−5.269×10N ⋅m2．确定最大正应力：σ=Mmax = M max,α= 66mm=0.611max32W σ=Mmax =2×πD32(1−α4)5.268N ⋅m108m m=24.71×106P a =24.71M P a max2W=π(1=08×10−3m ) 2×(1−0.6114) 327－7图示矩形截面简支梁,承受均布载荷q 作用.若已知q ＝2 kN/m ,l ＝3 m ,h ＝2b＝240mm .试求：截面竖放(图c)和横放(图b)时梁内地最大正应力,并加以比较. 习题7－7图解：1．计算最大弯矩： ql22×103N/m ×(3m )2M max ===2.25×103N ⋅m882．确定最大正应力：3平放：σ =M max = 2.25×10N ⋅m ×6 =3.91×106Pa=3.91MPamax 2−3 −32hb6240×10 m ×(120×10 m )4 ⎝ ⎠ 竖放：σ=M max = 2.25×103N ⋅m ×6=1.95×106Pa=1.95MPamax 2−3 −32 bh 6120×10m ×(240×10 m )3．比较平放与竖放时地最大正应力：σmax (平放) () 3.91 ≈2.07－8圆截面外伸梁,图中尺寸单位为mm .已知F P ＝10kN ,q ＝ M解：σ( )M max1 =32×30.65×10N ⋅m =113[σ] max 实＝ W 1π(140×10-3m )3σ( )M max2 = 32×20×103N ⋅m =100.3×106Pa=100.3MPa<[σ] max 空＝⎡⎛⎞⎤ W 2π(140×10-3m )3⎢1− ⎢⎣ 100⎜140⎟⎥所以,梁地强度是安全地.7－9悬臂梁AB 受力如图所示,其中F P ＝10kN ,M ＝70kN ·m ,a ＝3m .梁横截面地形状及尺寸均示于图中(单位为mm),C 为截面形心,截面对中性轴地惯性矩I z ＝1.02×108mm 4,拉伸许用应力[σ]＋＝40MPa ,压缩许用应力[σ]－＝120MPa .试校核梁地强度是否安全.解：画弯矩图如图所示：σ σ σ σ M (kN.m) C 截面30x+max =30×10N ⋅m ×96.4×10 m =28.35×106Pa=28.35MPa 1.02×108×10−12m 43−3 D 截面 －max =30×10N ⋅m ×153.6×10m =45.17×106Pa=45.17MPa 1.02×108×10−12m 43−3 +max =40×10N ⋅m ×153.6×10m =60.24×106Pa=60.24MPa>[σ] 1.02×108×10−12m 43−3－ max =40×10N ⋅m ×96.4×10 m =37.8×106Pa=37.8MPa 1.02×108×10−12m 4所以,梁地强度不安全.7－10由No.10BC 连接,BC 杆在C 处用铰链悬挂[σ]＝160MPa ,试求:M8max P习题7－10图解：画弯矩图如图所示：对于梁：M max =0.5qσ=M max ≤[σ], 0.5q ≤[σ] max WW[σ]W 160×106×49×10−6q ≤ ==15.68×103N/m=15.68kN/m 0.50.5对于杆： σ=F N ≤[σ],4F B =4×2.25q ≤[σ] maxA πd 2 πd 2πd 2×[σ] π×(20×10-3)2×160×106q ≤ ==22.34×103N/m=22.34kN/m4×2.254×2.25所以结构地许可载荷为[q ]=15.68kN/m7－11 图示外伸梁承受集中载荷F P 作用,尺寸如图所示.已知F P ＝20kN ,许用应力[σ]＝160MPa ,试选择工字钢地号码. 习题7－11图解：M =F ×1m=20×103N ×1m=20×103N ⋅m σmax =M maxW≤[σ], F ×1m 20×103×1m W ≥ P ==0.125×10－3m 3＝125cm 3[σ] 所以,选择No.16 工字钢. 160×106Pa7－12图示之AB 为简支梁,当载荷F P 直接作用在梁地跨度中点时,梁内最大弯曲正应力超过许用应力30％.为减小AB 梁内地最大正应力,在AB 梁配置一辅助梁CD ,CD 也可以 习题7－12图看作是简支梁.试求辅助梁地长度a .解：1．没有辅助梁时σmax=M max≤[σ], WF P l4 =1.30[σ] W σmax=M max≤[σ], WF P l(3−2a ) 2=[σ]W F P l (3−2a ) F P l2= 4=[σ]W 1.30×W 1.30×(3−2a )=3a =1.384m7－13一跳板左端铰接,中间为可移动支承.为使体重不同地跳水者站在跳板前端在跳板中所产生地最大弯矩M zmax 均相同,问距离a 应怎样变化? 习题7－13图解：最大弯矩发生在可移动简支点B 处.（见图a 、b ）设不同体重分别为W ,W +ΔW ,则有,W (l −a )=(W +ΔW )(l −a −Δa ) ABW A整理后得 a 图 Δa = ΔW(W +ΔW )b 图(l −a ) 此即为相邻跳水者跳水时,可动点B 地调节距离Δa 与他们体重间地关系.7－14利用弯曲内力地知识,说明为何将标准双杠地尺寸设计成a=l /4.M MF习题7－14图解：双杠使用时,可视为外伸梁..A C Bb 图 若将a 地长度设计能达到下述情况为最经济、省工： M +=M −, max max即正负弯矩地绝对值相等,杠为等值杆.当a=l /4时,+ max− max=F P l /4（如图a,在中间面C ）； =F P l /4（发生在图b 所示受力情况下地A 面或B 面）.7－15图示二悬臂梁地截面均为矩形(b×h ),但(a)梁为钢质,(b)梁为木质.试写出危险截面上地最大拉应力与最大压应力地表达式,并注明其位置.二梁地弹性模量分别为E 、 E .P FP习题7－15图解：（1）两悬臂梁均为静定梁,故应力与材料弹性常数无关.（2）两悬臂梁均发生平面弯曲,危险面均在固定端处.σ σ σ σ 6 I 6I （3）钢梁： （4）木梁：+ max− max=6F P l bh 2 =6F P l bh 2（在固定端处顶边诸点） （在固定端处底边诸点） + max − max=6F P l hb 2=6F Pl hb 2（在固定端处后侧边诸点） （在固定端处前侧边诸点） 7－16T 形截面铸铁梁受力如图所示,其截面地I z=2.59×10−6m 4.试作该梁地内力图,求出梁内地最大拉应力和最大压应力,并指出它们地位置.画出危险截面上地正应力分布图.习题7－16图解：（1）求支座约束力F RA =37.5kN, F RB =112.5kN（2）作内力图,剪力图、弯矩图分别见习题7－16解图b 、c . （3）求所最大正应力和最小正应力E 、B 两截面分别发生最大正弯矩与最大负弯矩.所以,两个截面均有可能是危险截面.σ+=M E y2=14×10 ×142=76.8MPa （在E 截面下缘）z2.59×107σ−=M B y 2 =25×10 ×142=−137MPa （在B 截面下缘）z 2.59×107正应力分布图见图d.σ σ σ y m (a)AqEBD2m 1m50kN37.5kN⊕(b)⊕Ө1 62.5kN43.6MPa(d)(c)14kN·my 2⊕Ө25 kN·m 76.8MPa137MPa习题7－16解图7－17.在横放和竖放两种情况下,(a)比较许用弯曲力偶矩m O 绘出危险截面上地正应力分布图.解：(a)F R A2M (b) Өy 1(c)y 235y 1y 2σ习题7－17解图33（1）求支座约束力F RA=FRB=mOkN 5（2）作弯矩图见习题7－17解图b 所示. （3）竖放下地许用弯曲力偶矩m O由型钢表查得 从b 图中得：W =269.6×103 mm 3M =3m O由强度条件maxσmax =5 M maxW≤[σ] m ≤5W [σ]=5×269.6×10×160=71.89kN ⋅mO33（4）横放下地许用弯曲力偶矩m O由型钢表查得由强度条件W =30.61×103 mm 3m ≤5W [σ]=5×30.61×10 ×160=8.16kN ⋅mO33危险截面上地正应力分布图见图c.7－18制动装置地杠杆用直径d =30mm 地销钉支承在B 处.若杠杆地许用应力 [σ]=140MPa ,销钉地剪切许用应力[τ]=100MPa ,求许可载荷[F P1],[F P2].F P1F P2习题7－18图解：（1）求F P1 与F P2地关系4杠杠平衡时有：F P1×1000=F P2×250, （2）作弯矩图,如图 a 所示F P2 =4F P11000F（3σmax =M max W≤[σ]20×603 (20×303−)W = 1212=1.05×104mm 330 1000F p1W≤[σ] F ≤W [σ]=1.05×10×140=1.47kN P11000 1000∴F P2 ≤5.88kN（4）校核销钉地剪切强度剪切强度条件：F Q τmax = A≤[τ] 其中,F=5F=3.675mm 2 Q2P13 ∴τmax=3.675×10706.86=5.2MPa<[τ]则,销钉安全.（5）杠杆系统地许可载荷为[FP1]=1.47kN,[FP2]=5.88kN.上一章返回总目录下一章。

第7章直梁弯曲本章要点●理解弯曲的概念和实例●掌握截面法求剪力和弯矩●掌握剪力方程和弯矩方向，剪力图和弯矩图●掌握横力弯曲（剪切弯曲）时正应力和切应力的计算●掌握横力弯曲变形的计算●掌握提高弯曲强度的措施,7.1梁的类型及计算简图7.1.1对称弯曲的概念承受设备及起吊重量的桥式起重机的大梁（图7-1）、承受转子重量的电机轴（图7-2）等，在工作时最容易发生的变形是弯曲。

其受力特点是：杆件都是受到与杆轴线相垂直的外力（横向力）或外力偶的作用。

其变形为杆轴线由直线变成曲线，这种变形称为弯曲变形。

图7-1 桥式起重机的大梁图7-2 承受转子重量的电机轴工程中的梁，其横截面通常都有一纵向对称轴。

该对称轴与梁的轴线组成梁的纵向对称面（图7-3）。

外力或外力偶作用在梁的纵向对称平面内，则梁变形后的轴线在此平面内弯曲成一平面曲线，这种弯曲称为对称弯曲。

图7-3 对称弯曲7.1.2梁上的载荷作用在梁上的载荷可以简化为以下三种类型：(1)集中力；(2)集中力偶；(3)分布载荷，如图7-4a所示。

7.1.3梁的基本形式1.简支梁梁的一端为固定铰链支座，另一端为活动铰链支座。

如图7-4a所示。

2.外伸梁梁的支座和简支梁相同，只是梁的一端或两端伸出在支座之外。

如图7-4b所示。

3.悬臂梁梁的一端固定，另一端自由。

如图7-4c所示。

在对称弯曲的情况下，梁的主动力与约束反力构成平面力系。

上述简支梁、外伸梁和悬臂梁的约束反力，都能由静力平衡方程确定，因此，又称为静定梁。

在工程实际中，有时为了提高梁的强度和刚度，采取增加梁的支承的办法，此时静力平衡方程就不足以确定梁的全部约束反力，这种梁称为静不定梁或超静定梁。

7.2梁弯曲时的内力7.2.1剪力和弯矩现以图7-5所示的简支梁为例来研究各横截面上的内力。

P1、P2和P3为作用于梁上的载荷，R A和R B为两端的支座反力。

为了显示出横截面上的内力，沿截面mm假想地把梁分成两部分，并以左段为研究对象。