弯曲正应力切应力与强度条件演示文稿
- 格式:ppt
- 大小:4.60 MB
- 文档页数:154




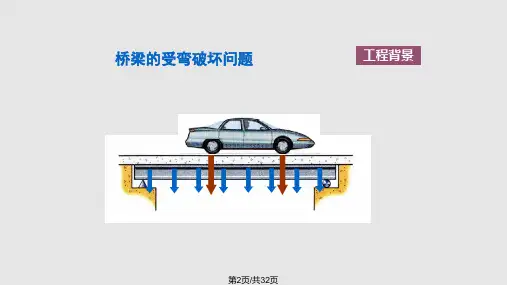



第18讲教学方案——弯曲切应力、弯曲强度条件§7-3 弯曲切应力梁受横弯曲时,虽然横截面上既有正应力σ,又有剪应力 τ。
但一般情况下,剪应力对梁的强度和变形的影响属于次要因素,因此对由剪力引起的剪应力,不再用变形、物理和静力关系进行推导,而是在承认正应力公式(6-2)仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。
1.矩形截面梁对于图6-5所示的矩形截面梁,横截面上作用剪力Q 。
现分析距中性轴z 为y 的横线1aa 上的剪应力分布情况。
根据剪应力成对定理,横线1aa 两端的剪应力必与截面两侧边相切,即与剪力Q 的方向一致。
由于对称的关系,横线1aa 中点处的剪应力也必与Q 的方向相同。
根据这三点剪应力的方向,可以设想1aa 线上各点剪应力的方向皆平行于剪力Q 。
又因截面高度h 大于宽度b ,剪应力的数值沿横线1aa 不可能有太大变化,可以认为是均匀分布的。
基于上述分析,可作如下假设:1)横截面上任一点处的剪应力方向均平行于剪力 Q 。
2)剪应力沿截面宽度均匀分布。
基于上述假定得到的解,与精确解相比有足够的精确度。
从图6-6a 的横弯梁中截出dx 微段,其左右截面上的内力如图6-6b 所示。
梁的横截面尺寸如图6-6c 所示,现欲求距中性轴z 为y 的横线1aa 处的剪应力 τ。
过1aa 用平行于中性层的纵截面11cc aa 自dx 微段中截出一微块(图6-6d )。
根据剪应力成对定理,微块的纵截面上存在均匀分布的剪应力 τ'。
微块左右侧面上正应力的合力分别为1N 和2N ,其中*1I 1**z zAzA S I M dA I My dA N ===⎰⎰σ (a ) *1II 2)()(**z z Az A S I dM M dA I y dM M dA N +=+==⎰⎰σ (b)式中,*A 为微块的侧面面积,)(II I σσ为面积*A 中距中性轴为 1y 处的正应力,⎰=*1*A z dA y S 。