材料力学_邓宗白_纯弯曲时的正应力

实验七纯弯曲梁的正应力实验[DOC]
实验目的：研究梁的中间点和两端点载荷作用下，现对象梁的变形和应力响应关系；测量梁的悬臂梁跨度；实现双轴载荷下梁的变形和应力的测量。

实验原理：该实验中的梁采用的是纯弯曲（非支承梁），根据应力方程和变形方程，可将变形和应力计算出来；悬臂梁跨径由始及终支点的水平位移量和圆半径决定。

实验仪器：梁材、载荷架、千分表、探头等测试器具。

实验步骤：
1. 将测试材料准备好，将梁安放到载荷架上，并调节支点的位置，使梁跨径恒定。

2. 调节载荷架，给两端点施加线性载荷，以产生纯弯的梁曲线。

3. 使用千分表和探头记录梁曲线的支点位置，从而计算梁跨径。

4. 根据应力方程和变形方程，计算梁中间点和两端点处的应力和变形量。

实验结果：
通过测量和计算，实验获得以下结果：
梁跨度：397 mm
中间点应力：234 MPa
两端点应力：110 MPa。

纯-弯曲梁的正应力实验本实验旨在研究弯曲梁在受力时的正应力分布情况，通过实验数据的测量及分析，探讨影响梁正应力分布的因素，并对梁的强度进行评估。

1. 实验原理1.1 弯曲梁正应力分析弯曲梁是一种常用的结构元件，例如桥梁、楼层结构等，她受到外力的作用会发生弯曲形变，产生正应力和剪应力。

弯曲梁的正应力是沿着截面法向的应力，在梁的顶部为拉应力，底部为压应力。

正应力的计算公式如下：$$\sigma = \frac{My}{I}$$其中，$\sigma$为正应力，$M$为弯矩，$y$为受力点到截面重心的距离，$I$为截面惯性矩。

弯曲梁正应力的分布情况受到多种因素的影响，主要包括：① 梁材料的弹性模量：弹性模量越大，弯曲梁的刚度越大，相同外力作用下，梁的形变和正应力都会相应减小。

② 梁截面形状和尺寸：梁截面的惯性矩影响正应力的大小和分布情况。

截面抗弯性能越强，正应力越小。

③ 受力位置和方向：受力位置和作用方向是影响正应力大小和分布情况的重要因素。

不同位置和方向的外力作用会导致不同的正应力分布规律。

2. 实验设备和方法本实验采用的主要设备有：弯曲梁试验机、电子天平、千分尺等。

2.2 实验步骤1. 准备弯曲梁样品，将其加工成常用的矩形截面和半圆形截面，分别测量其截面形状和尺寸。

2. 调整弯曲梁试验机，设置好取样位置和取样方式。

3. 将弯曲梁放入试验机，设置试验参数，包括荷重大小、位移速率等。

4. 开始试验，记录每个荷载下的跨中挠度和荷载大小，并计算出弯矩大小。

5. 在试验过程中，用电子天平测量梁的重量，并用千分尺对梁的跨中直径和截面高度进行测量，计算出截面惯性矩。

6. 根据测量数据，计算出每个荷载下的正应力，并绘制出正应力分布图。

3. 结果分析3.1 实验数据记录本实验用常见的矩形和半圆形弯曲梁进行了试验，记录了不同工况下的荷载和跨中挠度等数据。

根据数据计算得出弯矩以及正应力等数据，具体数据结果如下表：1. 矩形截面弯曲梁（1）弯曲梁在起始荷载下出现了微小的振动，但并未发生失稳。

实验六纯弯曲梁的正应力实验一、实验目的1. 梁在纯弯曲时横截面上正应力大小和分布规律；2. 验证纯弯曲梁的正应力计算公式；3. 测定泊松比μ；4. 掌握电测法的基本原理；二、实验设备1. 材料力学多功能实验台；2. 静态数字电阻应变仪一台；3. 矩形截面梁；4. 游标卡尺；三、实验原理1. 测定弯曲正应力本实验采用的是低碳钢制成的矩形截面试件，当力F 作用在辅助梁中央A 点时，通过辅助梁将压力F 分解为两个集中力2/F 并分别作用于主梁（试件）的B 、C 两点。

实验装置受力简图如下图所示。

根据内力分析，BC 段上剪力0=S F ，弯矩Fa M 21=，因此梁的BC 段发生纯弯曲。

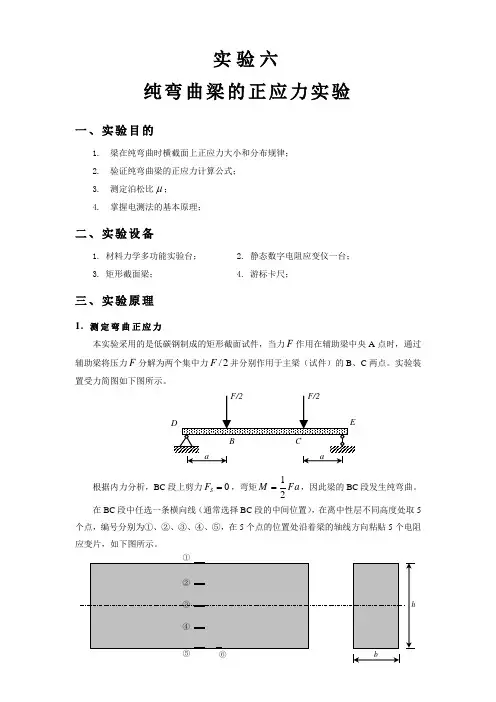
在BC 段中任选一条横向线（通常选择BC 段的中间位置），在离中性层不同高度处取5个点，编号分别为①、②、③、④、⑤，在5个点的位置处沿着梁的轴线方向粘贴5个电阻应变片，如下图所示。

D C B a F/2F/2E a ⑥ ⑤ ①② ④ ③ hb根据单向受力假设，梁横截面上各点均处于单向应力状态，应用轴向拉伸时的胡克定律，即可通过测定的各点应变，计算出相应的实验应力。

采用增量法，各点的实测应力增量表达式为：i i E 实实εσ∆=∆式中：i 为测量点的编号，i ＝1、2、3、4、5；i 实ε∆ 为各点的实测应变平均增量；为各点的实测应力平均增量； 纯弯梁横截面上正应力的理论表达式为：z i i I y M ⋅=σ ; 增量表达式为： zi i I y M ⋅∆=∆σ 通过同一点实测应力的增量与理论应力增量计算结果比较，算出相对误差，即验证纯弯曲梁的正应力计算公式。

以截面高度为纵坐标，应力大小为横坐标，建立平面坐标系。

将5个不同测点通过计算得到的实测应力平均增量以及各测点的测量高度分别作为横坐标和纵坐标标画在坐标平面内，并连成曲线，即可与横截面上应力理论分布情况进行比较。

2. 测定泊松比在梁的下边缘纵向应变片⑤附近，沿着梁的宽度方向粘贴一片电阻应变片⑥（电阻应变片⑥也可贴在梁的上边缘），测出沿宽度方向的应变，利用公式εεν'=，确定泊松比。

纯弯曲梁正应力实验报告数据实验目的：
本实验旨在通过对纯弯曲梁的正应力进行实验研究，探索材料力学的基本原理。

实验原理：
纯弯曲梁是指在弯曲变形过程中，仅发生弯曲变形，不发生剪切变形。

在实验中，通过在材料中施加外力，使得梁发生弯曲变形，进而分析材料的正应力。

实验步骤：
1. 准备实验设备并进行校准。

2. 安装试件，并在试件固定支点处施加相应的外力。

3. 使用光学显微镜等设备观察试件在弯曲过程中的变形情况，并记录数据。

4. 结束实验并进行数据分析和总结。

实验结果：
经过对实验数据的统计和分析，得出试件的正应力如下：
点位正应力
1 10.5 MPa
2 12.8 MPa
3 11.2 MPa
4 9.6 MPa
5 11.9 MPa
分析与总结：
根据实验结果，可以得出正应力随着弯曲程度的增加而变大的结论。

通过分析实验数据，可以进一步了解材料的力学特性，为未来的工程设计和材料选择提供科学依据。

结论：
通过对纯弯曲梁正应力的实验研究，成功得出了试件在不同点位处的正应力，结论表明弯曲程度与正应力呈正相关关系。

在未来的工程实践中，将会更加注重材料力学研究，以提高工程设计和选择的准确性和可靠性。

实验三纯弯曲梁横截面上正应力的分布规律实验
一､实验目的:
1.测定梁在纯弯曲时横截面上正应力大小和分布规律;
2.验证纯弯梁的正应力计算公式;
二.实验仪器设备:
1.CLDT-C材料力学多功能实验台
2. XL2118A/B应力&应变综合参数测试仪
3.BLK-1/1t拉压力传感器
三､弯曲梁简图:
图3-1
已知: ､､､､
在梁的纯弯曲段内(或)截面处粘贴五片电阻片,即､､､､｡贴在中性层处,实验时依次测出1､2､3､4､5点的应变,计算出应力｡
四､测量电桥原理
构件的应变值一般均很小,所以,应变片电阻变化率也很小,需用专门仪器进行测量,测量应变片的电阻变化率的仪器称为电阻应变仪,其测量电路为惠斯顿电桥,如图所示｡
如图所示,电桥四个桥臂的电阻分别为､､和,在､端接电源,､端为输出端｡
设､间的电压降为则经流电阻､的电流分别为,､,所以､两端的电压降分别为
,所以､端的输出电压为
当电桥输出电压时,称为电桥平衡｡故电桥平衡条件为或设电桥在接上电阻､､
和时处于平衡状态,即满足平衡条件｡当上述电阻分别改变､､和时
略去高阶微量后可得
(当时)
上式代表电桥的输出电压与各臂电阻改变量的一般关系｡
在进行电测实验时, 有时将粘贴在构件上的四个相同规格的应变片同时接入测量电桥,当构件受力后,设上述应变片感受到的
应变分别为､､､相应的电阻改变量分别为､､和,应变仪的读数为
以上为全桥测量的读数,如果是半桥测量,则读数为
所谓半桥测量是将应变片和放入仪器内部,和测量片接入电桥,接入､和､组成半桥测量
五､理论和实验计算
理论计算
､､?､､
实验值计算:
图3-3。