当前位置：文档之家 › 尺寸链计算例题及习题

尺寸链计算例题及习题

  • 格式：ppt
  • 大小：469.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

第10章工艺尺寸链计算题-精选文档

第10章工艺尺寸链计算题-精选文档

环名 A（增环） x（减环） B（封闭环）
基本尺寸 50 40 10
上偏差 0 +0.19 0
下偏差 -0.17 0 -0.36
2.工序基准是尚待加工的设计基准
例3.
加工一齿轮内孔和键槽 有关加工工序如下 2 ) 插键槽保证尺寸 3 ) 热处理 。 4） 磨内孔至图纸尺寸 求工序尺寸
解：
1）列尺寸链 2）判断各环性质
0 0.016
H1
H0
D2
R1
R2
a）
b）
图5.32 渗碳层深度尺寸换算
mm
解： 1）列尺寸链 2）判断各环性质 H0是最终的渗碳层厚度，是间 接保证的，因此是封闭环；H1、 R2为增环；R1为减环。 3）计算 环名 H1（增环） 基本尺寸 0.7 19 19.2 0.5 上偏差 +0.25 0 0 +0.3 下偏差 +0.008 -0.008 -0.05 0
R2（增环） D2/2
R1（减环） D1/2
0 . 250 最终结果 ：H 0 . 7 mm 1 0 . 008 H0（封闭环）
与封闭环方向相 同者为减环，相 反者为增环。
， 设计尺寸为 ：
0 . 05 0
：
D1 A1 D1 A1
R1 R 2
D 2 40 0 0 . 05 mm , H 43 . 3 0 0 . 2 mm 。 1 ) 镗内孔至 D 1 39 . 6 A 1。 D 2 40
0 . 05 0
A
例5.如图所示偏心零件 ， 表面 A要求渗碳 处理 ， 渗碳层深度规定为 0.5 ~ 0.8mm 。 与此有关的加工过程如 下： 1） 精车 A面， 保证直径尺寸 D1 38 .4 0 0.1 mm 2） 渗碳处理 ， 控制渗碳层深度 H 1 3） 精磨 A面， 保证直径尺寸 D2 38 确定 H 1的数值 。

尺寸链例题

尺寸链例题

2
EI 5 )
( 0 . 22 0 . 16 ) ( 0 . 25 0 . 048 0 . 048 ) 0 . 726 mm
校核结果符合要求。 最后结果为(单位均为mm)
A1 140
0 0 . 25
mm
A 2 A 5 5 0 . 048 mm
0
A 3 101
0 . 22 0
mm
A 4 50
0 . 16 0
mm
A0 10
0 . 726
mm
(3)按式(7-4)、式(7-5)计算封闭环的极限偏差 ES0＝ES3-(EI1+EI2+EI4+EI5) ＝+0.18mm-(-0.13-0.075-0.04-0.075)mm ＝+0.50mm EI0＝EI3-(ES1+ES2+ES4+ES5) ＝+0.02mm-(0+0+0+0) mm ＝+0.02 mm
0 . 04 0 . 12
mm
，内孔尺寸 mm，求壁厚A0。
mm
解 (1)确定封闭环、组成 环、画尺寸链图：车外圆和 镗内孔后就形成了壁厚，因 此，壁厚A0是封闭环。
取半径组成尺寸链，此时 A1、A2的极限尺寸均按半值 计算： A
1
35
2
A2 2 30
0 . 02 0 . 06
(4)按式(7-6)计算封闭环的公差 T0＝T1+T2+T3+T4+T5 =(0.13+0.075+0.16+0.075+0.04)mm ＝0.48mm 校核结果表明，封闭环的上、下偏差及公差均已超过规定范围， 必须调整组成环的极限偏差。

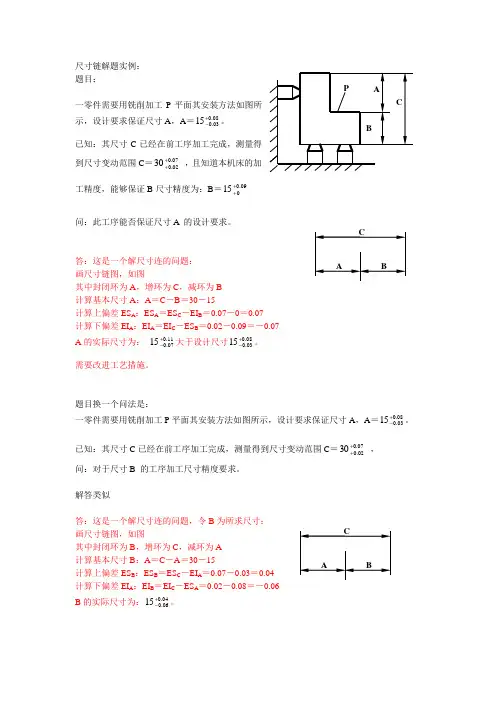
电大机械制造基础尺寸链解题实例：

电大机械制造基础尺寸链解题实例：

尺寸链解题实例：题目：一零件需要用铣削加工P 平面其安装方法如图所示，设计要求保证尺寸A ，A ＝80.003.015+-。

已知：其尺寸C 已经在前工序加工完成，测量得到尺寸变动范围C ＝07.002.030++ ，且知道本机床的加工精度，能够保证B 尺寸精度为：B ＝09.0015++问：此工序能否保证尺寸A 的设计要求。

答：这是一个解尺寸连的问题：画尺寸链图，如图其中封闭环为A ，增环为C ，减环为B计算基本尺寸A ：A ＝C －B ＝30－15计算上偏差ES A ：ES A ＝ES C －EI B ＝0.07－0＝0.07计算下偏差EI A ：EI A ＝EI C －ES B ＝0.02－0.09＝－0.07A 的实际尺寸为： 11.007.015+-大于设计尺寸80.003.015+-。

需要改进工艺措施。

题目换一个问法是：一零件需要用铣削加工P 平面其安装方法如图所示，设计要求保证尺寸A ，A ＝80.003.015+-。

已知：其尺寸C 已经在前工序加工完成，测量得到尺寸变动范围C ＝07.002.030++ ， 问：对于尺寸B 的工序加工尺寸精度要求。

解答类似答：这是一个解尺寸连的问题，令B 为所求尺寸：画尺寸链图，如图其中封闭环为B ，增环为C ，减环为A计算基本尺寸B ：A ＝C －A ＝30－15计算上偏差ES B ：ES B ＝ES C －EI A ＝0.07－0.03＝0.04计算下偏差EI A ：EI B ＝EI C －ES A ＝0.02－0.08＝－0.06B 的实际尺寸为：04.060.015+-。

尺寸链练习题

尺寸链练习题

t=4+0.16
封闭环
增环
t H
ESH=0.098 下偏差0= EIH+0.004-0
EIH=-0.004
H 4.2500..009084
14
0.012 0.004
增环
14.25
0 0.05
减环
5.图5为轴套类零件，在车床上已加工好外圆、内孔及各 端面，现需在铣床铣出右端槽并保证5-0.06及26±0.3的尺 寸，求试切调刀时的度量尺寸H、A及上、下偏差。
16-0.025、0.8+0.2为增环，d/2为减环。
d/2 16-0.025
2）计算 基本尺寸 0.5= 16 +0.8 –d/2
d/2= 16.3 上偏差0.3= 0+0.2-EId/2
EId/2= -0.1 下偏差0= -0.025+0-ESd/2
ESd/2= -0.025
d
/
2
16
.30.025 0.1
图4
解： 1）确定封闭环：加工时间接保证的尺寸为t=4+0.16。画 出尺寸链图。
t H
14
0.012 0.004
14.25
0 0.05
2）判断增减环 ：1400..001024
、H
为增环
，14.25
0 0.05
为减环。
3）计算
基本尺寸 4= H+14-14.25 H=4.25
上偏差0.16= ESH+0.012-(-0.05)
0.0175 0.005
为减环。
16 0.0175 0.005
t
15.900.07
2）计算 基本尺寸 0.1= t +15.9 –16

尺寸链计算题

尺寸链计算题
2.下图所示为某轴端，其要求为外径φ 25 0 0.014 ，外圆渗碳层深度 0.9～1.1mm， − 工艺过程如下： 工序Ⅰ，粗车外圆至φ 26 0 0.28 − 工序Ⅱ，精车外圆至φ 25.3 00.084 工序Ⅲ，划键槽线 工序Ⅳ，铣键槽深度至尺寸 A 工序Ⅴ，渗碳处理，深度为 t 工序Ⅵ，磨外圆至φ 25 0 0.014 − 试求： 1）用深度尺测量槽深尺寸 A （ （2）渗碳时控制的工艺渗碳层深度 t
B 25 8
B-3 -0.04
0
0
2、解： （1）a 建立尺寸链：
6
+0.035 0
（4 分）
1 2 .5 - 0 . 0 0 7
0
1 2 .6 5 - 0 . 0 4 2
0
21 . 2 - 0 .1 4
0
A
b 21.2 为封闭环, （1 分）12.5、12.65 为增环，A 为减环。 21.2=12.5+12.65-A A=3.95 0=0+0-EIA EIA=0 -0.14=-0.007-0.042-ESA ESA=0.091 c 故工序尺寸 A=3.95 0
+0.091
（1 分） （1 分） （1 分） （1 分） （1 分）
mm
(2) a 建立尺寸链：
1 2 . 7 -0. 04 2 t 0.9 1 2. 5 -0 .00 7
b 0.9 为封闭环, （1 分）12.5、 t 为增环，12.65 为减环。 0.9=12.5+t-12.65 t=0.75 0.2=0+ESt-（-0.042） ESt=0.158 0=-0.007+EIt-0 EIt=0.007 c 故工序尺寸 t=0.75 + 0.007 mm 计算结果完全正确，可以直接给分 （ 计算结果完全正确，可以直接给分）

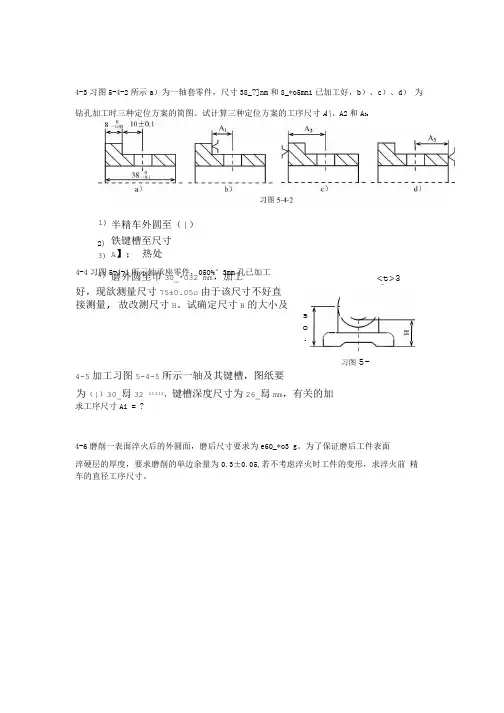
工艺尺寸链习题及答案.doc

工艺尺寸链习题及答案.doc

4-4习图5-4-4所示轴承座零件，05O%°3mm 孔已加工 好，现欲测量尺寸75±0.05o 由于该尺寸不好直接测量, 故改测尺寸H 。

试确定尺寸H 的大小及偏差。

4-5加工习图5-4-5所示一轴及其键槽，图纸要为（|）30_舄32 11111，键槽深度尺寸为26_舄mm ，有关的加1) 半精车外圆至（|）2) 3)铁键槽至尺寸A 】； 热处理；4) 磨外圆至巾30_*032 mm ，加工完毕。

4-3习图5-4-2所示a ）为一轴套零件，尺寸38_?]nm 和8_*o5mni 已加工好，b ）、c ）、d ） 为钻孔加工时三种定位方案的简图。

试计算三种定位方案的工序尺寸A\、A2和A 3O求工序尺寸Ai = ?4-6磨削一表面淬火后的外圆面，磨后尺寸要求为e6O_*o3 g 。

为了保证磨后工件表面 淬硬层的厚度，要求磨削的单边余量为0.3±0.05,若不考虑淬火时工件的变形，求淬火前 精车的直径工序尺寸。

习图5-4-4<t>3O +jj 0so.4-3答案：1)图b：基准重合，定位误差ADW = 0 , A] = 10±0.1mm；2)图c：尺寸A2, 10+0.1 和8_膈构成一个尺寸链(见习解图5X4-2c),其中尺寸10+0.1是封闭环，尺寸A?和8是组成环，且A? 为增环，8_膈为减环。

由直线尺寸链极值算法基本尺寸计算公式，有：10= Ai —8, —A2=18mm由直线尺寸链极值算法偏差计算公式：0.1=ESA2 — (-0.05), 一ESA2=0.05mm;-0.1 =EIA2一0, 一ElA2=-0.1 mm。

故：A2 =1mm3)图d：尺寸A3, 10+0.1, 8_舄5和构成一个尺寸链(见习解图5X4-2d),其中尺寸10+0.1是封闭环，尺寸A3, 8_膈和38*是组成环，且38*为增环，A3和8_膈为减环。

由直线尺寸链极值算法基本尺寸计算公式，有：10= 38— (A3+8), -^A3=28mm 由直线尺寸链极值算法偏差计算公式，有：0.1=0- (EIA3+ (-0.05)), 一EIA3=-0.05mm;-0.1 = -0.1 — (ES A3+O), —>ESA3=0O故：A3 = 28_Q05 mm4-4答案：尺寸75+0.05> H和半径R组成一个尺寸链，其中尺寸75+0.05是间接得到的，是封闭环。

尺寸链计算例题及习题

尺寸链计算例题及习题
显然，第三个尺寸链给分的公差最小，的公差就可按尺寸链3来定。 （即的公差为0.042mm）。当的公差确定后，的偏差布置是根据尺寸 链1中的布置方式来分布（即mm，和设计尺寸mm的布置形式是一致 的）。
3. 计算其余的工序尺寸及偏差
1. 由尺寸链计算公式：
2. 封闭环的基本尺寸＝所有增环的基本尺寸－所有减环的基本尺寸；
图1 设计尺寸
作业3 如图2－40所示为某模 板简图，镗削两孔O1, O2时 均以底面M为定位基准，试标 注镗两孔的工序尺寸。检验两 孔孔距时，因其测量不便，试 标注出测量尺寸A的大小及偏 差。若A超差，可否直接判定 该模板为废品？
作业3 下图所示轴套 工件，在车床上已加工 好外圆、内孔及各表面， 现需在铣床上以端面A 定位铣出表面C，保证 尺寸20-0.2mm试计算 铣此缺口时的工序尺寸。
2. 基本尺寸计算：43.6=A+20－19. 8mm
3. A＝43．4
4. 上偏差计算：+0. 34=Bs(A)＋0. 025－0
5. Bs (A)＝＋0. 315mm
6. 下偏差计算：0=B,(A)+0－0. 05
7. Bx (A)＝＋0. 05mm
8. 所以
A=43.4+0.05+0.315mm
作业4 要求在轴上铣一 个键槽，如下图所示。加 工顺序为车削外圆A1＝； 铣键槽尺寸为A2；磨外 圆A3＝Ø70-00.06mm， 要求磨外圆后保证键槽尺 寸为N＝62-00.3mm,求 键槽尺寸A2。
整体活动预期
3. 封闭环的上偏差＝所有增环的上偏差－所有减环的下偏差；
4. 封闭环的下偏差＝所有增环的下偏差－所有减环的上偏差。
5. 计算尺寸链2 得mm

尺寸链公差计算案例

尺寸链公差计算案例

尺寸链公差计算案例
假设我们要计算一条尺寸链的公差，该尺寸链包含4个零件距离，它们是A、B、C和D。

首先，我们需要明确每个零件的尺寸和公差。

假设A的尺寸
为10mm，公差为±0.1mm；B的尺寸为15mm，公差为
±0.2mm；C的尺寸为20mm，公差为±0.3mm；D的尺寸为
25mm，公差为±0.1mm。

接下来，我们需要计算每个零件的尺寸范围。

对于A零件来说，其下限是10 - 0.1 = 9.9mm，上限是10 + 0.1 = 10.1mm。

同样地，B的下限是15 - 0.2 = 14.8mm，上限是15 + 0.2 =
15.2mm；C的下限是20 - 0.3 = 19.7mm，上限是20 + 0.3 = 20.3mm；D的下限是25 - 0.1 = 24.9mm，上限是25 + 0.1 = 25.1mm。

然后，我们可以计算尺寸链整体的下限和上限。

下限是各个零件下限之和，即9.9 + 14.8 + 19.7 + 24.9 = 69.3mm；上限是各
个零件上限之和，即10.1 + 15.2 + 20.3 + 25.1 = 70.7mm。

最后，我们可以得到尺寸链的公差范围。

公差是上限减去下限，即70.7 - 69.3 = 1.4mm。

因此，该尺寸链的公差为±1.4mm。

这只是一个简单的尺寸链公差计算案例，实际情况可能更加复杂，需要考虑更多的零件和更多的尺寸限制。

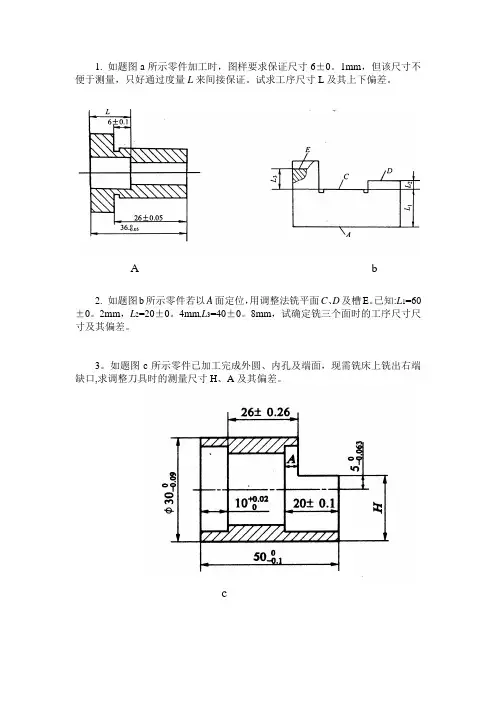
工艺尺寸链习题【范本模板】

工艺尺寸链习题【范本模板】

1. 如题图a所示零件加工时，图样要求保证尺寸6±0。

1mm，但该尺寸不便于测量，只好通过度量L来间接保证。

试求工序尺寸L及其上下偏差。

A b2. 如题图b所示零件若以A面定位，用调整法铣平面C、D及槽E。

已知:L1=60±0。

2mm，L2=20±0。

4mm,L3=40±0。

8mm，试确定铣三个面时的工序尺寸尺寸及其偏差。

3。

如题图c所示零件已加工完成外圆、内孔及端面，现需铣床上铣出右端缺口,求调整刀具时的测量尺寸H、A及其偏差。

c4。

如题图d 中小轴的工艺过程为：车外圆至φ01.05.30-mm ，铣键槽深度为TH H +0,热处理，磨外圆至φ0.036+0.01630+mm 。

设磨后外圆与车后外圆的同轴度公差为φ0。

05mm ，求保证键槽深度设计尺寸2.004+mm 的键槽深度TH H +0.D E5。

如题图e 所示衬套,材料为20Cr ，φ0.021030+mm 内孔表面要求磨削后保证渗碳层深度3.008.0+mm,试求：（1)磨削前精镗工序尺寸及偏差。

磨削余量0。

03，精镗的经济精度9级 (2）精镗后热处理时渗碳层的深度.1.如下图所示轴套零件的轴向尺寸，其外圆、内孔及端面均已加工。

试求：当以A面定位钻直径为φ10mm孔时的工序尺寸A1及其偏差32mm，渗碳深度为0.5~08mm，现为2。

设某一零件图上规定的外园直径为φ0-0.05了使此零件可与另一零件同炉进行渗碳，限定其工艺渗碳深度为0。

8~1mm。

试计算渗碳前车削工序的工序尺寸。

3。

某零件工艺过程如下:（1）精车外圆至φ-0.08425.3；（2）划键槽线；（3）铣键槽至12AA T±；(4)渗碳深度t+t T;(5）磨外圆至φ-0.01425，要求渗碳深度0。

9～1。

1mm(单边）。

试求：（1）计算洗键槽时用深度尺测量槽深尺寸12A A T ±(2）渗碳时应控制的工艺渗碳层深度t + 0 t T。

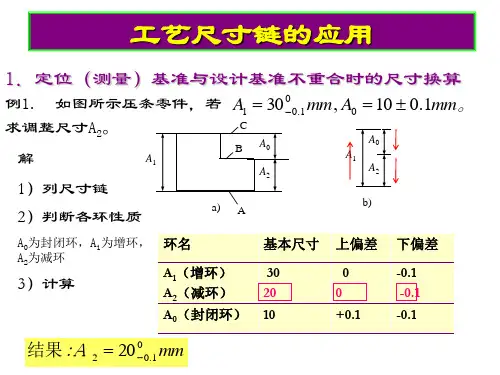
工艺尺寸链计算题

工艺尺寸链计算题

环名 2L2（增环） 增环）
基本尺寸 上偏差 下偏差 66 -0.15 -0.28
最后结果：L 2 = 33−0..075 mm − 0 140
4．有表面处理工序的工艺尺寸链计算 表面处理是指表面渗碳﹑渗氮等渗入类以及镀 铬﹑镀锌等镀层类的表面处理。渗入类表面处 理通常在精加工以前完成渗入，精加工后应使 渗入层厚度符合设计要求，因此设计要求的渗 入层厚度为封闭环。镀层类表面处理在大多数 情况下是通过控制电镀工艺参数来保证镀层厚 度的，因此最后获得的电镀后的零件尺寸为封 闭环。
工艺尺寸链的应用
例2. 图所示零件，设计尺寸为10-0.360。因尺寸不便测量， 图所示零件，设计尺寸为10 A0 = A − A 改测尺寸x。试确定尺寸x的数值和公差。 z =1 z j = n +1 j
n m
∑
n
∑
解： 1）列尺寸链 B A 2）判断各环性质 X
ES 0 = ∑ ES z −
z =1
下偏差 +0.04 0 -0.015 0 0
0 结果：A 1 = 43.1+0..16 = 43.140.12 mm + 0 04
例4. 连杆厚度尺寸要求如图所示。为了使连杆在加工过程中安装方便，开始加 工时小头的厚度亦按大头要求加工，到加工后期再将小头铣薄。有关的加 工工序如下：
30±0.1
a）
下偏差 +0.025 0 0 0
R1（减环） 键槽深度H为磨内孔间接 R1（减环） 得到，是封闭环。其余各 D1/2 环的判断如图。 H（封闭环） 封闭环）
3）计算
+ 最后结果为 : A1 = 43.1+0..175 = 43.125 0 0.15 mm + 0 025

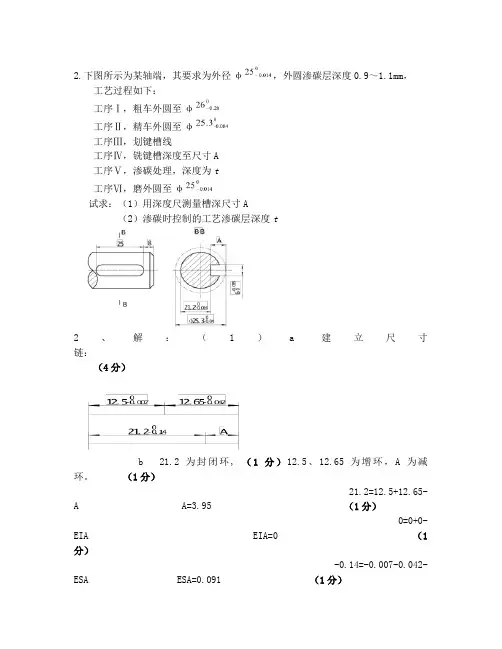
尺寸链和统计分析计算题

尺寸链和统计分析计算题

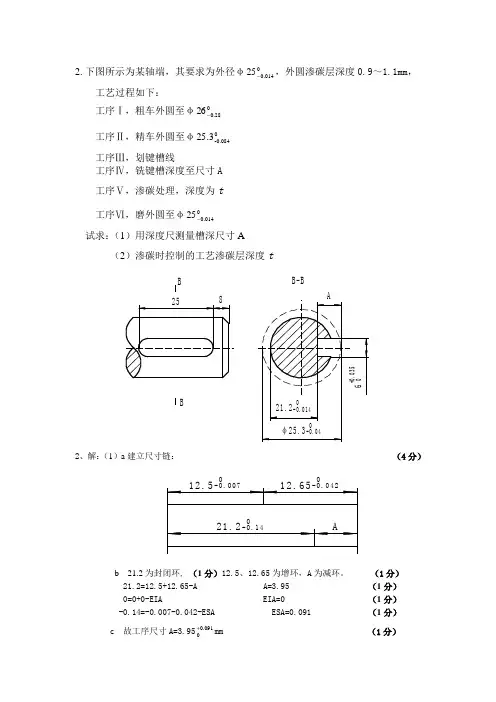
2.下图所示为某轴端，其要求为外径φ，外圆渗碳层深度0.9～1.1mm，工艺过程如下：工序Ⅰ，粗车外圆至φ工序Ⅱ，精车外圆至φ工序Ⅲ，划键槽线工序Ⅳ，铣键槽深度至尺寸A工序Ⅴ，渗碳处理，深度为t工序Ⅵ，磨外圆至φ试求：（1）用深度尺测量槽深尺寸A（2）渗碳时控制的工艺渗碳层深度t2、解：（1）a建立尺寸链：（4分）b 21.2为封闭环,（1分）12.5、12.65为增环，A为减环。

（1分）21.2=12.5+12.65-A A=3.95 （1分）0=0+0-EIA EIA=0 （1分）-0.14=-0.007-0.042-ESA ESA=0.091 （1分）c 故工序尺寸A=3.95mm （1分）(2) a 建立尺寸链：b 0.9为封闭环,（1分）12.5、 t为增环，12.65为减环。

（1分）0.9=12.5+t-12.65 t=0.750.2=0+ESt-（-0.042） ESt=0.1580=-0.007+EIt-0 EIt=0.007c故工序尺寸t=0.75mm（计算结果完全正确，可以直接给分）加工误差的统计分析1.在两台相同的自动车床上加工一批小轴的外圆，要求保证直径φ11±0.02mm，第一台加工1000件，其直径尺寸按正态分布，平均值=11.005mm,均方差=0.004mm。

第二台加工500件，其直径尺寸也按正态分布，且=11.015mm，=0.0025mm。

试求：（1）在同一图上画出两台机床加工的两批工件的尺寸分布图，确定工序能力系数，并指出哪台机床的精度高？（2）加工中有无变值系统误差和常值系统误差，有无废品产生？如有，可否修复？并分析其产生的原因及提出改进的方法。

解：两台机床上加工的两批小轴，其加工直径的分布曲线如下图所示。

（2分）（1）第一台机床的精度 6σ=6×0.004=0.024mm（1分）第二台机床的精度 6σ=6×0.0025=0.015mm（1分）所以，6σ<6σ,故第二台机床的精度高。

工艺尺寸链计算题

工艺尺寸链计算题

A
B
X
B
B
A
X
B
A
X
B
A
X
B
X
环名
基本尺寸
上偏差
下偏差
A（增环） x（减环）
50 40
0 +0.19
-0.17 0
B（封闭环）
10
0
-0.36
工艺尺寸链的应用
解： 1）列尺寸链 2）判断各环性质 键槽深度H为磨内孔间接得到，是封闭环。其余各环的判断如图。 3）计算
R1
R2
R1
R1
19.2
0
-0.05
H0（封闭环）
0.5
+0.3
0
L1
L2
L2
L0
环名
基本尺寸
上偏差
下偏差
2L2（增环）
66
-0.15
-0.28
L1（减环）
36
+0.18
-0.25
L0（封闭环）
30
+0.1
-0.1
4．有表面处理工序的工艺尺寸链计算
表面处理是指表面渗碳﹑渗氮等渗入类以及镀铬﹑镀锌等镀层类的表面处理。渗入类表面处理通常在精加工以前完成渗入，精加工后应使渗入层厚度符合设计要求，因此设计要求的渗入层厚度为封闭环。镀层类表面处理在大多数情况下是通过控制电镀工艺参数来保证镀层厚度的，因此最后获得的电镀后的零件尺寸为封闭环。
R2
R1
R2
R1
R2
R1
R2
R1
R2
R1
R1
R1
R1
H
D2
D1
A1
环名
基本尺寸
上偏差

尺寸链计算例题

尺寸链计算例题

尺寸链计算例题
尺寸链计算是一种用于计算物体尺寸关系的方法，其中一个物体的尺寸可以通过另一个物体的尺寸和比例关系来推导出来。

以下是一个尺寸链计算的例题：
问题：一个正方形纸片的边长为3厘米，将其对角线分割成两段，其中一段的长度是另一段长度的2倍，求两段的长度。

解答：首先，我们知道对角线可以将正方形分割成两个等边三角形。

设其中一段的长度为x厘米，则另一段的长度为2x厘米。

根据勾股定理，正方形的边长的平方等于对角线的两段长度的平方之和。

因此，有：
3^2 = x^2 + (2x)^2
9 = x^2 + 4x^2
9 = 5x^2
x^2 = 9 / 5
x = √(9/5)
因为边长不能为负数，所以x = √(9/5) ≈ 1.34。

因此，其中一段的长度约为1.34厘米，另一段的长度约为2.68厘米。

尺寸链例题#(精选.)

尺寸链例题#(精选.)

第五章 工艺规程设计例1:图示零件,2面设计尺寸为 2522.00 +mm ，尺寸60012.0-mm 已经保证，现以1面定位用调整法精铣2面，试计算工序尺寸。

解:(1)建立尺寸链设计尺寸2522.00 +mm 是间接保证的，是封闭环，A 1（60012.0-mm ）和A 2为组成环。

（2）计算根据 A 0＝∑=m i i A 1－∑-+=11n m i i A A 2 = A 1－A 0＝35ES 0＝∑=mi i ES 1－∑-+=11n m i i EI EI 2＝ES 1－ES 0＝－0.22 EI 0＝∑=mi i EI 1－∑-+=11n m i i ES ES 2＝EI 1－EI 0＝－0.12则：工序尺寸A 2＝3512.022.0--＝34.88010.0-mm 。

例2:下图所示工件外圆、内孔及端面均已加工完毕，本序加工A 面，保证设计尺寸8±0.1 mm 。

由于不便测量，现已B面作为测量基准，试求测量尺寸及其偏差。

解:（1）建立尺寸链设计尺寸8±0.1是mm 是封闭环，A 1、A 2、A 3是组成环。

（2）计算根据 A 0＝∑=m i i A 1－∑-+=11n m i i AA 1 = A 0－A 2＋A 3=18ES 0＝∑=m i i ES 1－∑-+=11n m i i EI ES 1=ES 0－ES 2＋EI 3=0EI 0＝∑=mi i EI 1－∑-+=11n m i i ES EI 1=EI 0－EI 2＋ES 3=－0.05 则：测量尺寸A 1＝180 05.0-＝17.9505.00 ＋ mm 。

例3：一带有键槽的内孔要淬火及磨削，其设计尺寸如图所示。

保证键槽尺寸034 0436..+ mm 的有关工艺过程如下： 1）镗内孔至中01 0396..ϕ＋（005 0198.R .＋）mm ； 2）插键槽至尺寸A 1；3）淬火（变形忽略不计）；4）磨内孔，同时保证内孔直径005 040.ϕ+（0025 020.R +）mm 和键槽深度 034 0436..+mm 两个设计尺寸的要求。

尺寸链练习题

尺寸链练习题

课堂练习： 1. 如图所示尺寸链简图，试计算组成环 A1 的基本尺寸及上下偏差。（已知： ， A0是封闭环）。 解：确定增减环 A1为增环、A2为减环
A2
A1
A0
2. 如图所示尺寸链简图，试计算封闭环 A0的 基本尺寸及上下偏差（已知： , ）。
A1 A0
A2 A3
3.如图所示尺寸链简图，试计算封闭环 A0 的基本尺寸及上下偏差。（已知： ， ）。
A4
例1：有一尺寸链如图所示， 0 已知 A 24 mm ， 1 0.4 0.2 ，
A2 180 A4 50 0.5 mm
0
A3 A2
mm A3 14 0.15mm A 0
A1
求封闭环A0的基本尺寸及其上下偏差。 解：确定增减环 A2 、A4为增环、A1、A3为减环 A0 = A2+A4-Aห้องสมุดไป่ตู้-A3 =18+50-24-14=30 mm ESA0 =+0.2+0-(-0.4)-(-0.15)=0.75 mm EIA0 =0+(-0.5)-0-(+0.15)=-0.65 mm 0.75 A0 30 0.65 mm 有 校核 T0 =0.75-(-0.65)=1.4 mm = 0-(-0.4)+0.2-0+0.15-(-0.15)+0-(-0.5)=1.4 mm 经校核计算正确。
A3
A0 A2 A1
4. 如图所示尺寸链简图，试计算封闭环 A0的基本尺寸及上下偏差。（已知： ， ， ）。
A1 A2 A3 A4 A0
例2：有一尺寸链如图所示，已知
A2
A1 620
0.10
mm
A1 A4
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.保证渗氮、渗碳层深度的工艺计
算 有些零件的表面需进行渗氮或渗碳 处理，并且要求精加工后要保持一 定的渗层深度。为此，必须确定渗 前加工的工序尺寸和热处理时的渗 层深度。
例2-5如图2-28a所示某零



件内孔，材料为 38CrMoAlA,孔径为 Ø1450+0.04 mm内孔表 面需要渗氮，渗氮层深度 为0. 3~0. 5mm。其加工 过程为 磨内孔至 Ø144.760+0.04mm； 2)渗氮，深度t1； 3）磨内孔至 Ø1450+0.04mm，并保 留渗层深度t0=0. 3～0. 5mm 。 试求渗氮时的深度t1。
表2－25 列表计算法
列号
名称 T EI ES A T A ES EI A A A A A
m n n 11 i i iji j i1 m ii m 11 jj
I 基本尺寸
Ⅱ 上偏差
Ⅲ 下偏差
3.计算其余的工序尺寸及偏差 由尺寸链计算公式：
封闭环的基本尺寸＝所有增环的基本尺寸－所有减



环的基本尺寸； 封闭环的上偏差＝所有增环的上偏差－所有减环的 下偏差； 封闭环的下偏差＝所有增环的下偏差－所有减环的 上偏差。 计算尺寸链2 得mm 计算尺寸链3 得mm 4.计算结果： mm mm mm 通过这种方法求解工序尺寸时简捷、明了，省去了 封闭环的判断，尺寸之间的联系一目了然。
解先列出尺寸链如图2－21b。要注意的是，当有直径尺寸时，

一般应考虑用半径尺寸来列尺寸链。因最后工序是直接保证 Ø400+0.05mm，间接保证43. 60+0.34mm，故43.6+0.3434 mm为封闭环，尺寸A和20+0.025mm为增环，19. 8+0.05mm为减环。利用基本公式计算可得 基本尺寸计算：43.6=A+20－19. 8mm A＝43．4 上偏差计算：+0. 34=Bs(A)＋0. 025－0 Bs (A)＝＋0. 315mm 下偏差计算：0=B,(A)+0－0. 05 Bx (A)＝＋0. 05mm 所以 A=43.4+0.05+0.315mm 按入体原则标注为：A=43.450+0.265mm
5.列表计算法 将式（2－1）、式（2－4）、式（2－5）、
式（2－6）改写成表2－25所示的竖式表， 计算时较为简明清晰。纵向各列中，最后一 行为该列以上各行相加的和；横向各行中， 第Ⅳ列为第Ⅱ列与第Ⅲ列之差；而最后一列 和最后一行则是进行综合验算的依据。在应 用这种竖式时需注意：将减环的有关数据填 入和算得的结果移出该表时，其基本尺寸前 应加“一”号；其上、下偏差对调位置后再 变号（“＋”变“一”，“一”变 “＋，’）。对增环、封闭环则无此要求。
作业2 根据设计尺寸（见图1），确定工序尺
寸（见下图）。
图1 设计尺寸
作业3 如图2－40所示为某模板简图，镗削
两孔O1, O2时均以底面M为定位基准，试标 注镗两孔的工序尺寸。检验两孔孔距时，因 其测量不便，试标注出测量尺寸A的大小及偏 差。若A超差，可否直接判定该模板为废品？
作业3 下图所示轴套工件，在车床上已加工
解 在孔的半径方向上画尺寸链如图2－28d



所示，显然t0=0. 3～0.5=0. 3+0.2mm是间接 获得，为封闭环。t1的求解如下： t1的基本尺寸：0. 3=72. 38+t1一72. 5 则t、＝0. 42mm t1的上偏差：＋0. 2 =＋0. 02+Bs1－0 则Bs1＝＋0. 18mm t1的下偏差：0=0+Bx1－0. 02 则 Bx1=+0. 02mm 所以t1 =0. 42+0.02+0.18mm；即渗层深度为 0. 44~0. 6mm 。
尺寸链计算例题及习题
例1-4如图2－27所示为齿轮内孔的局部简图，设计要求为：孔径
Ø400+0.05mm，键槽深度尺寸为43. 60+0.34mm，其加工顺序为 1)镗内孔至Ø39.60+0.1mm；2)插键槽至尺寸A； 3)热处理，淬火；4)磨内孔至Ø400+0.05 试确定插键槽的工序尺寸A。
好外圆、内孔及各表面，现需在铣床上以端 面A定位铣出表面C，保证尺寸20-0.2mm试 计算铣此缺口时的工序尺寸。

作业4 要求在轴上铣一个键槽，如下图所示。加工
顺序为车削外圆A1＝Ø70.5-00.10mm；铣键槽尺 寸为A2；磨外圆A3＝Ø70-00.06mm，要求磨外圆 后保证键槽尺寸为N＝62-00.3mm,求键槽尺寸A2。
2.确定公共环的偏差
通过分析三个尺寸链可知为公共环（即三个尺寸链
都含有）根据封闭环的公差等于所有组成环公差之 和的理论，在定的偏差时要看这三个尺寸链中哪个 尺寸链给分的公差最小，的公差就按该尺寸链来定。 如果按公差平均分配的原则，在尺寸链1中给分的 公差为0.07mm；在尺寸链2中给分的公差为 0.05mm；在尺寸链3中给分的公差为0.042mm。 显然，第三个尺寸链给分的公差最小，的公差就可 按尺寸链3来定。（即的公差为0.042mm）。当的 公差确定后，的偏差布置是根据尺寸链1中的布置 方式来分布（即mm，和设计尺寸mm的布置形式是 一致的）。
Ⅳ 公差
数据 代 A 号 环的名称
ES
EI
T
ห้องสมุดไป่ตู้增环
减环
封闭环 A∑ ESA∑ EIA∑ TA∑
确定工序尺寸的一种新方法 当零件的设计基准与工艺基准不重合时，工艺规程编制的关键环节之一
是工序尺寸及偏差的确定。用传统的尺寸链计算方法求解工序尺寸时， 首先要判断封闭环，即要判断在直接保证某一个工序尺寸的同时，间接 保证的尺寸。这个过程对初学者来说既麻烦又容易出错。笔者根据多年 的工作实践总结出一种易掌握、易操作、易计算的确定工序尺寸的新方 法，现通过实例介绍如下。 例：根据实际尺寸（图a），确定工序尺寸（图b）
解：1.建立尺寸链
首先把每个设计尺寸都看作是封闭环，然后依次用(图a)中的
设计尺寸去(图b)中对应与该尺寸有关的工序尺寸。从而很方 便地建立起了尺寸链（有几个设计尺寸就可以建立几个尺寸 链）。 将mm这个设计尺寸看作封闭环（带框的尺寸）建立的尺寸 链为（尺寸链1）；将mm这个设计尺寸看作封闭环（带框的 尺寸）建立的尺寸链为（尺寸链2）；将 mm这个设计尺寸 看作封闭环（带框的尺寸）建立的尺寸链为（尺寸链3）。