当前位置：文档之家 › 正弦稳态电路的分析

正弦稳态电路的分析

  • 格式：docx
  • 大小：222.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

第2章 正弦稳态电路的分析

第2章 正弦稳态电路的分析

u
l
L是一个与i、ψ无关的常数。若线圈中含有铁磁物质，则 L与i、ψ有关，不是常数。 线圈的电感与线圈的形状，几何尺寸，匝数以及周 围物质的导磁性质有关，即 SN 2 L l l为密绕长线圈的长度（m），截面为S（m2)， 匝数为N，μ为介质的磁导率。
2．自感电动势
i(t)变化
ψ变化
产生eL(t)
波形图中 正半周 u ＞ 0 , i ＞ 0 (正值),说明实际方向与参考方向相同 负半周 u ＜ 0 , i ＜0 (负值),说明实际方向与参考方向相反
+
u
_
i,u T Um O
波形： Im

wt
可见:没有设定参考方向,正负值就没有意义,波形图也表达不出 它们的变化规律
2.1.2 正弦交流电量的三要素：
u U m cos( t + ) w U m e j (wt + )的实部 正弦电压u正好等于复数
u Re [U m e j (wt + ) ] Re [U m e jwt e j ] e jwt ] (令U U e j ) Re [U m m m
现在就把பைடு நூலகம்U m U m e j U m 称为正弦电压u的最大值相量
除法：模相除，角相减。
正弦交流电量的表示法 1、瞬时表达式(即时间的正弦或余弦函数式) 2、波形图(即时间的正弦或余弦函数曲线) 3、相量法(用复数表示正弦电量的方法) (1)复数与正弦量的关系
U m e j (wt + ) U m [cos(wt + ) + j sin(wt + )]
特殊相位关系：
u, i
u i O u, i u O u, i u iw t

第9章 正弦稳态电路的分析

第9章 正弦稳态电路的分析

§9.3 电路的相量图
例1： 应用相量图求图示电路的电压表的读数。
解：RC串联电路， I 设参考相量：= I 00 A I· + 8V + R 画相量图： + 1 · 先画参考相量： 如图（a）所示， U V jwC 11V I， 再画相量 UR , UR 与相量 I 同相， 再画相量 UC， UC 相量滞后 I90º 。 · UR 而 U=UR+UC ·I· 因此得直角三角形，所以 · UC U
1 | Y |= , φz = -φy |Z |
RL串联电路如图，求在w＝106rad/s时的等效并 例 联电路。 50W 解 RL串联电路的阻抗为：
X L = w L = 106 0.06 10-3 = 60W
0.06mH
Z = R jX L = 50 j60 = 78.150.20 W
z
但有受控源时，可能会出现
| j z | 90

或
| j y | 90

其实部将为负值，其等效电路要设定受控 源来表示实部；
注意
③一端口N0的两种参数Z和Y具有同等效用，彼 此可以等效互换，其极坐标形式表示的互换 条件为
| Z || Y |= 1
jz j y = 0
6. 阻抗（导纳）的串联和并联 ①阻抗的串联
1 1 Y= = = 0.0128 - 50.20 W Z 78.150.20 = 0.0082 - j0.0098 S 1 1 R = = = 122 W G 0.0082 1 L = = 0.102 mH 0.0098w
R’
L’
注意
①一端口N0的阻抗或导纳是由其内部的参数、结 构和正弦电源的频率决定的，在一般情况下， 其每一部分都是频率的函数，随频率而变； ②一端口N0中如不含受控源，则有 | j y | 90 | j | 90 或

电路原理-正弦稳态电路的分析

电路原理-正弦稳态电路的分析

对记录的数据进行分析，验证正 弦稳态电路的原理和性质。
实验结果与讨论
实验结果
通过实验观察和数据记录，可以 得出正弦稳态电路中电压和电流 的波形关系，以及元件参数对波
形的影响。
结果分析
对实验结果进行分析，验证正弦稳 态电路的基本原理，如欧姆定律、 基尔霍夫定律等。
实验讨论
讨论实验中可能存在的误差来源， 如电源稳定性、示波器的测量误差 等。同时，可以探讨如何减小误差、 提高实验精度的方法。
04 正弦稳态电路的分析实例
单相交流电路分析
总结词
分析单相交流电路时，需要计算电流、电压的有效值以及功率等参数，并考虑阻 抗、导纳和相位角等因素。
详细描述
在单相交流电路中，电压和电流都是时间的正弦函数。为了分析电路，我们需要 计算电流和电压的有效值，以及功率等参数。此外，还需要考虑阻抗、导纳和相 位角等因素，以便更准确地描述电路的性能。
实验步骤与操作
3. 观察波形
2. 连接电源
将电源连接到电路中，为电路提 供稳定的交流电压。
使用示波器观察电路中各点的电 压和电流波形，并记录数据。
4. 调整元件参数
通过调整电阻器、电容器和电感 器的参数，观察波形变化，并记 录数据。
1. 搭建正弦稳态电路
5. 分析数据
根据实验要求，使用电阻器、电 容器和电感器搭建正弦稳态电路。
相量法
1
相量法是一种分析正弦稳态电路的方法，通过引 入复数相量来表示正弦量，将时域问题转化为复 数域问题，简化计算过程。
2
相量法的核心思想是将正弦电压和电流表示为复 数形式的相量，并利用相量图进行电路分析。
3
相量法的优点在于能够直观地表示正弦量的相位 关系和幅度关系，简化计算过程，提高分析效率。

正弦稳态电路分析PPT课件

正弦稳态电路分析PPT课件
Q，并计算电源的视在功率S和功率因素cos 。
2
解法二： 采用阻抗Z计算；
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解：U s 100V I1 2 45（ A） I2 253.1（ A）
P1 I12R1 （ 2）2 5 10（W）
或： P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12（W）
或： P2 USI2 cos φ2=10 2 cos 53.1 12（W）
例：电路如图，已知 us (t) 10 2 sin 5（t V） ，求电阻R1，R2
消耗的功率，并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+

第九章正弦稳态电路分析

第九章正弦稳态电路分析

uL 176 2 sin ( 314t 163 )V
uC 352 2 sin ( 314 t 17 )V
通过计算可看出：
U C IX C 4.4 80 352V
I
U U R U L UC
UL
UR 53 U
而是 U U R U L U C (3)相量图 U L UC (4) P UI cos 220 4.4 cos ( 53)W
I
Im
Z R jX | Z | cos Z j | Z | sin Z R：电阻，X：电抗
(1) R、L、C元件的阻抗
Z R R R 0 Z L jL L90 1 1 ZC j 90 C C
（2）RLC串联电路的阻抗: 根据KVL 和相量形式的欧姆定律得
§9-3 正弦稳态电路的分析
正弦电流电路的稳态计算：利用相量形式的基尔霍夫电流 定律和电压定律以及电路元件相量形式的伏安关系。
分析方法：网孔电流法和节点电压法。 用网孔电流法时，应注意什么是自阻抗、互阻抗，特别是 互阻抗正负号与流经此阻抗的两网孔电流方向的关系：相 同取正，相反取负。对网孔中的电源，包括独立电压源、 独立电流源以及受控源，处理方法均与电阻电路的回路分 析法相同。
i 4.4 2 sin ( 314 t 73 )A
(2)
50 X L XC 40 - 80 arctan arctan -53 R 30
Z
U R IR 4.4 30V 132V
uR 132 2 sin ( 314t 73 )V
U L IX L 4.4 40 V 176V

正弦交流电路的稳态分析(课件)

正弦交流电路的稳态分析(课件)

02
正弦交流电的基本概念
正弦交流电的定义
正弦交流电
正弦交流电的产生
大小和方向随时间作正弦函数周期性 变化的电流。
通过交流发电机产生，当磁场和导体 线圈发生相对运动时，导体线圈中就 会产生正弦交流电。
正弦交流电的波形图
正弦交流电的波形图呈现正弦函数的 形状，随着时间的推移，电流值在正 弦波的最高点和最低点之间变化。
线性时不变正弦交流电路具有 叠加性、比例性和线性特性。
相量法分析正弦交流电路
相量法是一种分析正弦交流电 路的方法，通过引入复数和相 量，将时域的电压和电流表示
为复数形式的相量。
相量法的优点在于可以将正 弦交流电路中的复杂数学问 题简化为复数代数问题，从
而方便求解。
通过相量法，可以得出正弦交 流电路的阻抗、功率和相位等
未来研究的方向和展望
研究方向一
研究方向二
针对复杂正弦交流电路的稳态分析，深入 研究不同元件之间的相互影响，提高分析 精度。
结合新型材料在正弦交流电路中的应用， 研究其对电路性能的影响，探索新型材料 在优化电路性能方面的潜力。
研究方向三
研究方向四
结合现代计算技术和仿真软件，开发高效 、精确的正弦交流电路稳态分析方法和工 具。
正弦交流电路的稳态分析 (课件)
• 引言 • 正弦交流电的基本概念 • 正弦交流电路的稳态分析 • 实例分析 • 总结与展望
01
引言
主题简介
正弦交流电路
正弦交流电路是指电流和电压随时间按正弦规律变化的电路 。在日常生活和工业生产中，许多电源和负荷都是以正弦交 流电的形式存在。
稳态分析
稳态分析是电路分析的一个重要方面，主要研究电路在稳定 状态下各元件的电压、电流和功率等参数。对于正弦交流电 路，稳态分析涉及对电路中各元件的电压和电流进行傅里叶 变换，以得到各次谐波的幅值和相位。

正弦稳态电路的分析

正弦稳态电路的分析
I
+
U
-
+ UR R L +U - L C
+ UC -
U L
U
UC
U R
I
8.2 简单正弦稳态电路的分析、相量图
4、R-L-C并联交流电路
（1）电流、电压的关系 I IR I IL C
U
R
L
C
I I R I L IC 1 1 U( j C ) R j L
k 1
n
Gk j Bk
k 1 k 1
Yk Ik I Y
8.2 简单正弦稳态电路的分析、相量图
例1：写出下列电路阻抗和导纳的表达式。
R L1 C L2 R1 C1 R2 C2
(a)
Z R j L1 1 Y Z 1 1 j C j L2 Y
(b)
1 j C1 R1 1 Y 1 R2 1 j C 2
五、 功率因数（Power Factor）的提高
六、复功率(Complex Power)----VA
8.3
正弦稳态电路中的功率
8.3
正弦稳态电路中的功率
Power in Sinusoidal Steady State
一、瞬时功率(Instantaneous Power)----W
i
设 ：u i 2U costV 2 I cos( t ) A
（2）RLC串联电路的复数阻抗

I
+
U
-
+ UR R L +U - L
C + UC -
Z R j X L X C
8.2 简单正弦稳态电路的分析、相量图

正弦稳态电路的分析

正弦稳态电路的分析

正弦稳态电路的分析1.复数法分析：a. 复数电压和电流表示：将正弦波电流和电压表示为复数形式，即I = Im * exp(jωt)，V = Vm * exp(jωt)，其中Im和Vm为幅值，ω为角频率，j为虚数单位。

b.使用欧姆定律和基尔霍夫定律来建立复数表达式。

c.找到电路中的频域参数，如电阻、电感和电容等，并使用复数法计算电路中的电流和电压。

d.计算电源电压和电流的相位差，这会决定电路中的功率因数。

2.相量法分析：a.相量表示：将电路中的电流和电压表示为相量形式，即以幅值和相位角表示，例如I=Im∠θ，V=Vm∠θ。

b.使用欧姆定律和基尔霍夫定律来建立相量表达式。

c.对电路中的频域参数应用相量法，计算电路中的电流和电压。

d.计算电源电压和电流的相位差，以确定电路中的功率因数。

无论是复数法还是相量法，分析正弦稳态电路的关键是计算电路中的电流和电压的幅值和相位。

在计算过程中，需要使用复数代数、欧姆定律、基尔霍夫定律以及频域的电路参数等相关知识。

在实际应用中，正弦稳态电路的分析主要包括以下几个方面：1.交流电路中的电阻：电阻对交流电流的影响与直流电路相同，即按欧姆定律计算。

复数法计算时，电流和电压与频率无关，可以直接使用欧姆定律计算。

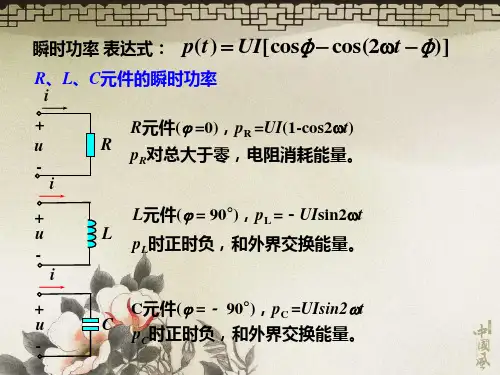
2.交流电路中的电感：电感器对交流电流的响应取决于电流的频率。

复数法计算电感电压和电流时，需要将频率变量引入到电感的阻抗中。

3.交流电路中的电容：电容器对交流电压的响应取决于电压的频率。

复数法计算电容电压和电流时，需要将频率变量引入到电容的阻抗中。

4.交流电路中的复数阻抗：电路中的电感、电容和电阻组成复数阻抗。

复数阻抗可以用来计算电路中的电流和电压。

根据欧姆定律和基尔霍夫定律，可以建立复数电流和电压之间的关系。

5.交流电路中的功率因数：功率因数是电路中有功功率与视在功率之比。

在分析正弦稳态电路时，可以计算电路中电源电压和电流的相位差，从而确定功率因数。

总结起来，正弦稳态电路的分析步骤包括选择复数法或相量法、建立复数或相量表达式、计算电流和电压的幅值和相位、计算功率因数等。

正弦稳态电路的分析

正弦稳态电路的分析

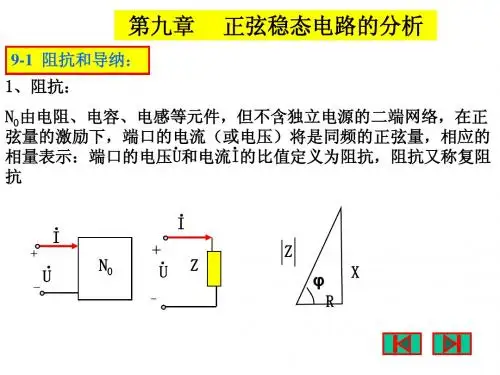
第九章正弦稳态电路的分析本章内容1．阻抗和导纳的概念2．阻抗的串并联及电路的相量图3．正弦稳态电路的分析4．瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5．串联和并联谐振本章重点：正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点：正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中，端口的电压相量与电流相量的比值定义为该一端口的阻抗（复阻抗），用Z表示。

式中：•U=U∠ϕu•I=I∠ϕI阻抗的模：Z= U/I，阻抗角：ϕZ= ϕu-ϕi 阻抗的代数式： Z=R+jX式中：R—电阻 X—电抗1．若网络N 0内只含单一元件，则单一元件的复阻抗（1）电阻的复阻抗：Z R =R（2）电感的复阻抗：Z L =ωj L=jX L X L =ωL —感抗 （3）电容的复阻抗：Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2．若网络N 0内为RLC 串联，则阻抗为（1）阻抗：Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见：阻抗Z 的实部为电阻R （R=Z cos ϕZ ），阻抗Z 的虚部为电抗X （X= R=Z sin ϕZ ），三者构成阻抗三角形 （2） 阻抗的模：Z =22)(C L X X R -+=22X R +=U/I （3）阻抗角：ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳：复阻抗的倒数定义为复导纳（电流相量与对应端口的电流相量的比值），用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模： Y =U I导纳角： Y ϕ=u i ϕϕ- 导纳的代数式： Y=G+JB式中：G —电导 B —电纳1．若网络N 0内只含单一元件，则单一元件的复阻抗 （1） 电阻的复导纳：Y R =G=1/R （2） 电感的复导纳：Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 （3）电容的复导纳：Z C ==ωj C =jB C B C =ωC —容纳2．若网络N 0内为RLC 并联，则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式：∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见：导纳Y 的实部为电导G （G=Y cos ϕY ），导纳Y 的虚部为电纳B （B= Y sin ϕY ），三者构成导纳三角形 （2）导纳的模：Y =22)(L C B B G -+=22B G +=I/U （3）阻抗角：ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换（自学）§9-2 阻抗（导纳）串联和并联阻抗的串并联与电阻的串并联的计算规则相同，只是要把电阻换成阻抗。

第九章 正弦稳态电路的分析

第九章 正弦稳态电路的分析

依据上述数据，还可求出 依据上述数据，还可求出R1、L1： ：
& Us Z1 = = 38∠ 75 0 & I1 Z 1 = R 1 + j ωL 1 R 1 = 9.84 36.71 L1 = = 116.9mH 314
9-5
正弦稳态电路的功率 。 i u －。
＋
设一端口N内部不含独立源，仅有 、 、 设一端口 内部不含独立源，仅有R、L、C 内部不含独立源 吸收的功率： 吸收的功率：p=ui（关联方向） （关联方向） i = 2I cos(ωt + Ψi ) 设u = 2U cos(ωt + Ψu )
u
ϕ = Ψu − Ψi )
) − UIsin(-ϕ ) sin( 2ωt + 2Ψ ) = UI cos ϕ{1 + cos[2( ωt + Ψ ]} + UI sin ϕ sin[2(ωt + Ψ )]
u u
平均功率又称有功功率 一周期内的平均值 1T 1T p = ∫ pdt = ∫ UI[ cos ϕ + cos( 2ωt + Ψu + Ψi )]dt =UI cos ϕ T0 T0 功率因数 cosϕ用λ = cosϕ 无功功率 ϑ = UIsinϕ 视在功功率 S = UI
& 1 I I 导纳：阻抗Z的倒数定义为导纳 Y 的倒数定义为导纳： 导纳：阻抗 的倒数定义为导纳： = = = ∠ψ i − ψ u = Y ∠ϕ y & Z U U Y的代数式可写为： 的代数式可写为： 的代数式可写为 Y = G + jB ← 电纳 ↑ 电导 电阻YR =
单个元件的导纳： 单个元件的导纳：
单个元件的阻抗： 单个元件的阻抗：

正弦稳态电路的分析

正弦稳态电路的分析

一、阻抗 1. 一端口的阻抗 不含独立电源N0 ，当它在正弦电源激励下处于稳 不含独立电源N 态时，端口的电压、电流都是同频率的正弦量， 态时，端口的电压、电流都是同频率的正弦量，即 u = 2U cos(ωt +ϕ ) U = U∠ϕ →ɺ
u u
9-1 阻抗与导纳
0
i = 2I cos(ωt +ϕi ) I = I∠ϕi →ɺ 则它的端电压相量与端电流相量的比 阻抗Z 值定义为该一端口N 值定义为该一端口N0的(复)阻抗Z，即
ɺ 解: 选择 U'作为参考相量
ɺ IR
ɺ U'
α =45°
ɺ IC
∵ωL = 200×0.25 = 50Ω= R ∴IR = IL 由几何关系得: 由几何关系得:
ɺ IL
ɺ US ɺ UC
ɺ ɺ ɺ IC = I R + I L ɺ ɺ ɺ US = U′ +UC
UC =US =100V, U′ =100 2V U′ ∴IR = IL = = 2 2A , IC = 2IR = 4A , R IC 1 UC ∴ = ,C= = 2×10−4 F = 200µF ωC IC ωUC
def
R jX
|Z|——阻抗 的模； ϕ Z ——阻抗角； 阻抗Z的模 阻抗角； 阻抗 的模； 阻抗角 R——等效电阻；X——等效电抗。 等效电阻； 等效电抗。 等效电阻 等效电抗 为实数， 称为感性阻抗， (R为实数，X>0称为感性阻抗，X<0称 为实数 X>0称为感性阻抗 X<0称
ɺ U U Z === = ∠(ϕu −ϕi ) =| Z | ∠ϕZ = R + jX ɺ I I
第九章 正弦稳态电路的分析

正弦交流电电路稳态分析

正弦交流电电路稳态分析
分析含有非线性元件的交流电路中电压、电流和功率的分布和计算。
详细描述
含有非线性元件的交流电路是指包含非线性电阻、非线性电感和非线性电容等元件的交流电路。在稳态分析中， 需要采用适当的数学方法来计算各元件的电压、电流和功率，并确定它们在含有非线性元件的交流电路中的分布 情况。
含有非线性元件的交流电路稳态分析
正弦交流电电路稳态分析
目 录
• 引言 • 正弦交流电基础知识 • 电路稳态分析方法 • 正弦交流电电路稳态分析实例 • 结论与展望
01 引言
背景介绍
正弦交流电的产生
交流发电机利用电磁感应原理将机械能转换为电能。当转子 绕组中的电流随时间变化时，就会产生旋转磁场，该磁场会 与定子绕组中的感应电流相互作用，从而产生正弦交流电。
02 03
详细描述
三相交流电路是指电源和负载之间的电压和电流在三个相位上变化的电 路。在稳态分析中，需要计算各相的电压、电流和功率，并确定它们在 三相电路中的分布情况。
总结词
考虑三相阻抗、三相感抗和三相容抗对电路的影响。
三相交流电路稳态分析
• 详细描述：在三相交流电路中，三相阻抗、三相感抗和三相容 抗是影响各相电压和电流分布的重要因素。三相阻抗包括电阻、 电感和电容在三相电路中的作用，而三相感抗和三相容抗则是 由于电感和电容产生的磁场和电场对电流的阻碍作用。
解决实际工程问题
在实际的电力系统和电子设备中，正弦交流电的应用非常广泛。因此，对正弦交流电电路 稳态分析的研究有助于解决实际工程问题，提高电力系统和电子设备的性能和稳定性。
推动相关领域的发展
正弦交流电电路稳态分析涉及到多个学科领域，如电路理论、电磁场理论、控制系统理论 等。因此，对正弦交流电电路稳态分析的研究有助于推动相关领域的发展，促进多学科交 叉融合。

正弦稳态电路分析解读

正弦稳态电路分析解读
i 10 2 cos(314 t 30 0 ) A
求：（1）正弦量的最大值、有效值； （2）角频率、周期、频率； （3）初相角、相位差。
解 ： （1）最大值 Um=220 2 V, Im=10
有效值 U=220V， I=10A
2A
（2）角频率ω=314 rad/s, 频率f=50Hz, 周期T=0.02s
根据有效值的定义有：
I 2 RT 0Ti2 Rdt
正弦电流的有效值为：
I
1 T
0Ti 2 dt
1 T
0T
I
2 m
cos2
(t
i)dt
I m 0.707 I m 2
同理，正弦电压的有效值为：
U Um 0.707Um 2
正弦电动势的有效值为：
E
Em 2
0.707 Em
在正弦量的三要素中，一般用有效值来代替最大值表示正 弦量的大小，在工程上，通常所说的正弦电压、电流的大 小都是指其有效值。
e Em cos(t e )
u U m cos(t u )
i I m cos(t i )
4.1.1 正弦量的三要素
正弦量的特征表现在变化的快慢、大小和初始值三个方面， 它们分别由角频率、幅值和初相来确定，统称为正弦量的 三要素。
以正弦电流为例
i Im cos(t i )
幅值
角频率
初相
的初始值
规定初相角的绝对值不超过
即 ≤≤
如果遇到初相角大于 时，应加 初相角小 于 时，应加 2
规定
2 ，如果遇到
来使初相角符合
4.1.2 正弦量的有效值
有效值用来表示正弦量大小
正弦电流的有效值：
让周期电流i和直流电流I分别通过两 个阻值相等的电阻R，如果在相同的 时间T内，两个电阻消耗的能量相等， 则称该直流电流I的值为周期电流i的 有效值。

正弦稳态分析-电路分析

正弦稳态分析-电路分析

第二节 电阻、电感和电容的相量形式的VCR
一、R元件：
设 : iR 2IR cos(ωt i) 则 : uR R iR 2RI R cos(ωt i )
U
R

RI R
u i
即: UR RIR
IR R UR
UR Ψi IR
二、L元件： 设 : iL 2IL cos(ωt i) ,
知：A a jb
则: A a 2 b2 , φ arctg b , A a 2 b2tg 1 b Aφ
a
a
若知：A Aφ
则: a A cos φ, b A sin φ, A A cos φ j A sin φ
（3）复数的四则运算 相等：两复数的实部和虚部分别相等。
则 45 30 15
解：i2 20cos(314t 30 90) 20cos(314t 60)
则 45 (60) 105
或i1
10sin( 314t 45 90) 则 135 30 105

10sin(
例2：(5+j4) ×(6+j3)=18+j39
2ndF CPLX 5 a 4 b × 6 a 3 b =显示“18” b 显示
“39”
例3： 3 j4 5(126.87)
3 +/- a 4 +/- b 2ndF →rθ 显示“5” b 显示“-126.8698…”
例4： 10 ∠-60° =5-j8.66…
同理
t
idt
的相量为:

I
jω

ωI

90
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第九章 正弦稳态电路的分析 1内容提要正弦稳态电路的分析应用相量法。

通过引入相量法，建立了阻抗和导纳的概 念，给出了 KCL 、KVL 和欧姆定律的相量形式，山于它们与直流电路分析中所 用的同一公式在形式上完全相同，因此能够把分析直流电路的方法、原理、定律, 例如，网孔法(回路法)、结点法、叠加定理、戴维宇定理、等效电源原理等等 直接应用于分析正弦电路的相量模型，其区别在于：⑴不直接引用电压电流的瞬 时表达式来表征各种关系，而是用对应的相量形式来表征各种关系；⑵相应的运 算不是代数运算，而是复数的运算，因而运算比直流复杂。

根据复数运算的特点, 可画岀相量图，利用相量图的儿何关系来帮助分析和简化计算，从而扩大了求解 问题的思路和方法。

⑶引入了一些新的概念，如平均功率、无功功率、视在功率、 复功率、最大功率传输、谐振等。

认识以上区别，对正弦稳态电路的分析是有益 的。

2例题例1求图示电路中各支路电流i ：, L, i 5il1-R 5Q 解：①画运算电路模型，取网孔电流L 、L 如图。

(5-/2)/. -5/. =100②列网孔方程： '「.-571+(5 + J 5)/2=-J 1OO可用行列式求解：i 一人=29.23 + J6.16 = 29.87Z11.90③ :.i,(r) = 27.73V2cos(^-56.31°) A i 2(r) =32.35^2 c os 伽 -115.35°) A i() = 29.87血 cos伽 + 11.90。

)A 当然此题也可以用结点电压法、或貝它方法。

例2图中电流i 和Uzi 。

已知：Usi = IOO5/2 COS6X Vq 2 =100V2COS (6X + 90°) Vy 100^0°i\ =100-5-ylOO 5 + j5 5-)2一5 ?()()=15.38- J23.07 = 27.73Z - 56.31° A 10+ J155 + )5i 2 =5-)2一5 100 一 J100 300-J5005-J2-5-5 5 + )5 io+，i5 =-13.85-;29.23 = 32.35Z-H5.35« A2U 2=100Z90°工频指f=50HZ(3) i = _^_ = .^S ^55'=L13Z81.87° A■ Z“+Z 15-J45+45④ U ZI =I(Z + Z 2) = 1.13Z81.870x (45 -丿30) = 61.11/48.18° V (-)用结点电压法 如图的参考结点.取独立结点电压为(Jzi ・— 11 1(D+ ------- )= i sz,z, z 3 z 2+z ':.U 71 =人/(丄 + 丄 + —1—)=--- = 61.19Z48.18()Z ，‘ 30 30 45 — )3012乞 41 82° 30I =_U^=61.19Z48.18-=113Z81 870 AZ 2+Z 45 — ）30注意：在用相量法运用复数形式进行+ — X 三运算时要特别细心，稍不注意，就会岀错，尤其是除法.建议大家很认真地多做几个题目，并且由代数表示法到极坐标表示法，步骤不要省略. 还有书上 Pagel98-199,例 9-5, 9-6, 9-7.例3如下图用实验法测左整流器参数的r 和L （也可以是任意阻抗参数）在工频下，使用取样 电阻"50 Q,现测得：V x =50V, V ：=80V, V 3=100V,求 r 和 L 。

①求％: % = isZ II z 3)=皿瓷餌七—43 v（-）用戴维南左理：求a, b 支路以外（左侧）的戴维南等效电路②求 Zcq ： Z cq = Z 2+(Zj II Z 3) = -J30 + 307TZ-45° =15-j45QU Z1 Z2 is “©-j3023 ?-j30 丁30。

可用结点法，回路法戴维南左理等方法. 21zJ45Q如 61.19Z4&18。

= 61.19Z 4&18°• ~~45 — J30 54.08Z-33.69°极易写作 1.13Z48.18°-33.69°= 1.13Z14.49°解：运用相量间关系= 80 = Jr2+(a)L)2③ |Z| =牛=100 = + 50尸 *(应)2=> r = ll X = coL = 79.24 QV・・・ L = — = 0.25/7CD如果不充分利用阻抗模值与电压电流有效值之间的关系，显然计算会复杂很多。

因为初相位并不知道。

再举一个利用相量图求解题目的例子。

例4如图正弦电路，已知电流表A,读数为1A,电路参数如图所示，试求电流表A和电压表 V的读数。

说明一点：交流电压、电流测岀的读数是什么值？一一有效值解：⑦以h作为参考相量，即令i^izo0 A 贝ij u R = loi, = iozo°U L = yioi, = 1OZ9O0②画相量图见右图U = U R +U L1 =10屁45° ・・・电压表V的读数= u = 14・4 V③L =亠二=屁135°' ■-J10I = i,+I2=lZ9O0 A /.电流表A的读数=1 A例5图示正弦电路中正弦电压Us二380V、f二50H乙电容可调，当C二80. 95 n F时，交流电流表A的读数最小，为2.59A,求图中交流电流表免的读数。

思考：只给出了数量关系，给出的并不是相量 （复数形式）。

显然应该在相量图上充分利用平而几 何知识来求解最方便。

方法一•利用相量图 以Us 作为参考相量 感性负载，故L 滞后Us — ••• c 改变，h 并不变，只改 显然：当Ic-Ii Simp,即i Ic= G ） c *Us=2 n f C ・Us=314 此时 1=2.59 A ・•・【I = J 厂+/「=A /2.592+9.662=10 A能否不用相量图，来求解呢？当然可以！ Page201,方法二 思路：I 最小，表示I Y |最小。

（I 1= I Y I • Us）Y = jCOC + ---- 1 -- = — --------- 7 - j —7-^——4- jCOC& + j 叫 R 「+（叫）2 &-+（况J2改变C,只改变Y 的虚部，导纳最小，意味着虚部为0, Us 和i 同相位。

取 U s =380Z0°JllJ I = 2.59Z0°.I c = jcoCUs = )314x 80.59 x 10" X 380= )9.66 Ai = i c +i 1 => 2.59/0° =丿966+1" =I] cos® + j(I, sin (p } +9.66)9.66fl. sin ^,=-9.66 j tg ^,=_259^^,=hcos0=2.59j] = ._2?9_. = IQ ACOS0除此之外，还可以求得Ri 和L“Z 1 =H^ = 38Z75°h:.R] = |Zjcos^2 = 38cos75° = 9.84 Q况]=Izjsiii (p 7 = 36.71 Q36.71 [[厶门 …・•. L. = -- = 116.9 mH1314例6图示正弦电路中，已知电压表、电流表、和功率表的读数分别为69. 3\\ 3A 和180叭8139 uF, /二50Hz,求电路中的R 、L 和整个电路的功率因数cos 讥画相量图,由于h 支路为 个相位角＜p ，ic 超前Us 90° 变ic 的有效值，且i= ii+ic 和Us 同相位时，i 最小，故 X 80.59 XI 0^X380=9.66 An i QAT P = UI cos（f）/. cos/ =——=——--- =0.866 （/）= ±30°UI 69.3x3由此，可以端口电压为参考相捲，画出相量图。

因为“可为正也可为负值，因此有两种情况。

解（一）用相量图•••◎ = ±30。

，由此画出向量图（如上图），注意电流人和/应有两种情况。

■因厶=coCU = 27flJ=3A = I,所以对应12和I的两种不同悄况可求出:12 = 3 A或12 = 21 sin 60° = 3y/3A(二)用解析法••• P = t/ZcosO. ••• cos ①=—=0.866. <D = ±30° UI根据等效导纳故可得到以下方程组••• UIcos^ = P又••• P = I;Rp _j20OTf = [6.67Qy)R2 +(coL)2 =—* -I_ 36・8〃M-[36.8m///.尺=200或6・67 L = 36.8mHcoLR2+(CO L)冷Z±30、例 7 图示电路，已知w v (r) = 50V2cos!0/V, z v (r) = 5%/2cos(10/+30°)A,尺=4C, 厶二 \H • R 》=2d C 2 =0.05F, R 、=2G, C 3=0.05F, & = 2G ,他=2G 。

试用节点法和回路法求支路电流小/3> i 6o 解（一）节点法由于节点③为虚节点，即U 注=-2i"故不需对该节点列节点方程，f/y =50Z0°V t人=5Z30°A , coL } = 10Q ,丄=丄=2Q 。

coC 2 coC 31 1-------- i —匕 I +( ----- 7~ + T D 血 R 七r j 2代入数值，解得U ta =34.3Z«14°V ,匕2=6・73Z — 13・2°,.・.人=丄(1 + j)t/n2=4.76Z31.8°A, U n3 = -213 = 9.52Z-148.2°V2・ U.一〃、/ 匕吐 5丄=Q.87Z8&0。

人，1(、= /.+ 人=4.6Z20.8°A1呂+ j 叫R _ cos30°用+(讥厂23.1厂 coL sin30°coC --- ------- v = ---------斤+(皿严 23.1R _ cos30° R 2+(CO L)2~23.1- coLsin30°COC ---- ; -------- 7 = -----------f/? = 20Q= 6.67L = 36.8/77/7L = 36・8mH则有] __________R 、+j 叫 *:.i}=0.87^cos(10/ + 88°)A, z3 = 4.76^2 cos(10/ + 31.8°)A,/6 =4.6%/2cosG 07 + 20.8°) A(-)回路法1 1 1 •・(& + R2-j + ---------------- 山 + RJi2 + g - J 〒爪=Us叫丄+阿叫R,&4厶1 + (Rq + & + je厶)厶2 一(R\ + jEjis = 2人=2/H代入数值，解得I iX=4.76Z31.8°A, I i2=4.6Z20.8°A ••• i\ =/f2-/s=0.87Z88.0°A, /3=Z n=4.76Z31.8°A, /6 = /2=4.6Z20.8°A3习题9-L在题图9J电路中，己知X C=10QX L=5QR=5Q电压表V I』勺读数为100V,试求电流表A和电压表V的读数.图9」9-2在题图9-2所示频率为500Hz的正弦稳态电路中,电流表A读数为1A,电压表Vi 和V 的读数分别为120V 和100V,试求L 和C.图9-29-3定性绘岀题图9-3电路的电压、电流相量图，当co=lOO,Uab=Ucd, 求电容C 的的值。