正弦稳态电路的分析

2
Y = 0.1 + j0.2S
0.025F 0.1S
0.02F
十、利用相量图求解电路
例 如图所示电路，uS 2US cost ，求输出电压 uO(t) 对 uS(t) 的相位关系。
C
解：（一）解析法
+
+
1
uS
R uO
–
–
（二）相量图法
U O②
I jC
+ US
U C
R
+ UO
–
–
I ①
③ U C
直流电阻电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
R11Im1 R12Im2 R1mImm uS11
R
21I
m1
R
22I
m2
R 2mImm
uS22
R m1Im1 R m2Im2 R mm Imm uSmm
正弦稳态电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
ZZ1211IImm11
Z12I m 2 Z 22I m 2
Z1m I mm Z 2 m I mm
U S11 U S22
Zm1Im1 Zm2Im2 Zmm Imm U Smm
例 uS = 6cos3000t V，求正弦稳态时的 i1 , i2 。
i1 1k
+2000–i1 i2
uS
(3)
Z
U I
U I
u i
= R + jX = |Z| Z
Z R2 X2
Z
arctg
X R
ZU I
Z = u – i
(4) 阻抗的性质

Z1=Z2=-j200Ω
14、如图所示14正弦稳态电路，R=XL=5Ω，I1=10A，
UC=100V，XC=10Ω，
试求U和I。
解：设 2=I2 A
=50 V
=100 2=10 A 1=10 A
所以，I= =10 AI12+I2=I22
易知 与 同相
U= UC=100 V
15、如图15a所示正弦稳态电路，R1=1KΩ，R2=2KΩ，L=1H，求Ucd=Uab时C的值。
解：电路的总阻抗为
Z=-jXC+ = +j( -XC)
当XC=1Ω和XC=2Ω，可以列出如下两个方程
(1)
(2)
解（1）、（2）得，R=2 Ω，XL=2Ω
4、图4所示工频正弦电流电路中，U=100V，感性负载Z1的电流I1=10A，功率因数λ1=0.5，R=20Ω。
（1）求电源发出的有功功率、电流I、功率因数λ
(3)u= u1+u2+u3的表达式
解：（1）将 ， 写成标准指数形式，即
=-100∠150°V=100∠-30°V
=-100+j100 V=100 ∠135°V
根据相量和正弦量的关系，可得
u1=50 cos(314t+60°) V，u2=100 cos(314t-30°) V
u3=200cos(314t+135°) V
解： =Y =( ) = 45°
I= A
11、列出图11所示电路相量形式的回路方程和结点方程。
解：设各回路方向如图所示。
回路方程如下：
（1）
（2）
（3）
（4）
- = S（5）
选结点0作为参考结点，结点方程如下:

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0， 纯电抗
X<0, j < 0 , 容性负载， 超前功率因数
例：cos j = 0.5 (滞后)，则j =60o(电压领先电流60o)。
一般用户： 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下： S Sk k 1
例：
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率，引入“复功率”
I
+

故电压表的读数为141.1V，电流表的读数为10A。




例二： 在图3．5-2(a)所示电路中，已知R1=48Ω ，R2=24Ω ，
R3=48Ω ,R4=2Ω ，
3
XL=2．8Ω ， U 1

=220∠0°V，U
2
=220∠-120°V，U

=220∠120°V。
试求感性负载上的电流L。
例一：
如下图所示电路中，已知I1=10A，UAB=100V。求电压表V和电 流表A的读数。
解：设

U AB 为参考相量，即 U AB =100∠0°V，则



U AB 0 I2 10 2 45 A, I1 10900 A 5 j5
I I1 I 2 10900 10 2 450 1000 A U c1 I ( j10) j100 V U U c1 U AB j100 V 100 V 100 2 450 V 141.1 450 V
§3．5正弦稳态电路的分析
3．5．1相量分析法 在正弦稳态电路的分析中，若电路中的所有元件都用阻
抗模型表示，电路中的所有电压和电流都用相量表示，所
得电路的相量模型将服从相量形式的欧姆定律和基尔霍夫 定律，此时列出的电路方程为线性的复数代数方程(称为相 量方程)，与电阻电路中的相应方程类似。这种基于电路的 相量模型对正弦稳态电路进行分析的方法称为相量分析法。
QC=-P(tanφ L-tanφ )
例：
(3．7-4)
已知某目光灯电路模型如图3．7-1(a)中的实线所示。图中L为铁心线圈，称 为镇流器，R为灯管的等效电阻。已知电源电压U=220V，f=50Hz，日

第9章 正弦稳态电路的分析 答案例 如图所示正弦稳态电路，已知I1=I2=10A,电阻R 上电压的初相位为零，求相量•I 和•S U 。

解： 电路中电阻R 和电容C 并联，且两端电压的初相为0。

由电阻和电容傻姑娘的电压与电流的相位关系可知：电阻电流•1I 与电压•R U 同相，电容电流•2I 超前电压•R U 相角90○，故ο0101∠=•I A ο90102∠=•I A由KCL 方程，有 ()101021j I I I +=+=•••A由KVL 方程，有 ︒•••∠==++-=+=9010010010010010010101j j I I j U S V例 如图所示正弦稳态电路，R 1=R 2=1Ω。

（1）当电源频率为f 0时，X C2=1Ω，理想电压表读数V 1=3V ，V 2=6V ，V 3=2V,求I S 。

（2）电路中电阻、电容和电感的值不变，现将电源的频率提高一倍，即为2 f 0，若想维持V 1的读数不变，I S 问应变为多少如果把电源的频率提高一倍，而维持V1的读数不变，即R1上的电压有效值U R1＝3V，那么R1上的电流的有效值I也不变，此时仍把•I设置为参考相量，故︒•∠=03I A。

由于L和C1上的电流•I不变，根据电感和电容上电压有效值与频率的关系，电源的频率提高一倍，电感上电压表的读数增大一倍，而电容上电压表的读数降为原来的一半，故电源得频率提高一倍，X C2也降为原来得一半，即所以例如图所示正弦稳态电路，已知I1＝10A，I2=20A，R2=5Ω，U=220V,并且总电压•U与总电流•I同相。

求电流I和R，X2，X C的值。

例 如图所示正弦稳态电路，已知有效值U 1=1002V, U=5002V ，I 2=30A ，电阻R=10Ω，求电抗X 1，X 2和X 3的值。

由电路可得两边取模得已知2550=U V ，所以6002=U V ，故有。

5.3.2 复数的概念 复数运算是正弦稳态电路分析法的数学工具，掌握复数运算和如何将正弦信号与复 数建立关系是关键。 1. 正弦信号与复数之间的关系 欧拉公式
e jx = cos x + j sin x
根据欧拉公式有
U me j(ωt+θi ) = U m cos(ωt + θi ) + jU m sin(ωt + θi )
n•
∑ ∑ I km = 0 或
Ik =0
k =1
k =1
KVL 相量形式（对于回路）
∑n • U km = 0
或
k =1
3. 电路元件的相量表示
•
•
电阻元件：U = R I
∑n • Uk =0
k =1
•
•
电感元件：U = jωL I
•
电容元件：U =
1
•
I =−j
1
•
I
jωC
ωC
4. 相量模型 所谓相量模型，就是将电路中正弦电压源和电流源用相量形式表示，电压变量和电 流变量用相量形式表示，电阻、电感和电容用阻抗形式表示。
电阻阻抗形式： Z R = R
电感阻抗形式： Z L = jωL
电容阻抗形式： ZC
=
1 jωC
=−j 1 ωC
5.3.4 电路谐振
•
•
谐振条件，对于二端口网络，端口电压U 与端口电流 I 同相位。根据这一条件
第五章 正弦稳态电路分析 •55•
可知，只有当阻抗的虚部为零才能满足这个条件。使虚部为 0 的频率为谐振频率。 谐振分为串联谐振和并联谐振。 串联谐振常用于无线接收设备中，并联谐振常用于带通滤波、选频电路等。

1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗（导纳） 分析阻抗（导纳）串、并联电路时，可以利用相关的 并联电路时， 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程，用相量平移求和法则，画出结点 方程， ③ 根据结点上的 方程 用相量平移求和法则， 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知：R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, （瞬时表达式）和各元件的 电路中的电流 瞬时表达式） 试求 电压相量； 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量；(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法： p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法： p UIcosϕ 恒定分量 恒定分量 u i
O

Q，并计算电源的视在功率S和功率因素cos 。
2
解法二： 采用阻抗Z计算；
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解：U s 100V I1 2 45（ A） I2 253.1（ A）
P1 I12R1 （ 2）2 5 10（W）
或： P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12（W）
或： P2 USI2 cos φ2=10 2 cos 53.1 12（W）
例：电路如图，已知 us (t) 10 2 sin 5（t V） ，求电阻R1，R2
消耗的功率，并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+

正弦稳态交流电路相量的研究实验
正弦稳态交流电路相量的研究实验
研究实验是一种从实际实验出发，用实际的电路构建和测量，以解决问题和探索新的机制的研究方法。

本文将介绍一种研究正弦稳态交流电路相量的研究实验过程，包括实验准备、实验操作、实验结果分析和实验结论等各个部分。

一、实验准备：
1、实验仪器：多功能实验电源、电阻测试仪、万用表、数字多用表、交流电压表、电子元件测试仪等。

2、实验电路：正弦稳态交流电路。

3、实验耗材：各种电阻、电容、变压器及相关电子元件等。

二、实验操作：
1、根据实验电路结构图，进行电路构建，注意接线的次序，确保电路的正确性。

2、将多功能实验电源调节至所需电压，使用电阻测试仪测量每条线路内的线路电阻，以确保电阻值的正确性。

3、使用万用表测量各相电压，使用数字多用表测量电流，以确保电压和电流的正确性。

4、使用交流电压表测量正弦波频率。

5、使用电子元件测试仪测量元件之间的相量。

三、实验结果分析：
1、通过测量电压和电流值，计算每条线路的有功功率、无功功
率和视在功率。

2、计算各相电压、电流和功率之间的相位差，以确定不同电压和电流间的相量。

3、通过计算不同元件之间的相量，得出正弦波频率的测量结果，以确定不同相量之间的差异。

四、实验结论：
通过上述实验可以得出，正弦稳态交流电路相量的测量结果与理论值接近，可以得出正弦稳态交流电路在实际情况下的表现与理论上的理论相符。

正弦稳态交流电路相量的研究实验报告实验目的。

本实验旨在通过对正弦稳态交流电路相量的研究，探索交流电路中电压和电流的相量特性，加深对交流电路中相量概念的理解，并验证相关理论知识。

实验原理。

正弦稳态交流电路是指在电压和电流都是正弦波的情况下，电路中各个元件的电压和电流也是正弦波，并且频率相同、相位差不变。

在正弦稳态交流电路中，电压和电流的相量可以用复数表示，其中实部表示电压或电流的幅值，虚部表示相位差。

电压和电流的相量之间存在幅值比和相位差的关系。

实验仪器和材料。

1. 交流电源。

2. 电阻、电感、电容等元件。

3. 示波器。

4. 万用表。

5. 直流电源。

6. 信号发生器。

实验步骤。

1. 搭建正弦稳态交流电路，包括电压源、电阻、电感和电容等元件。

2. 连接示波器，观察电压和电流的波形，并测量其幅值和相位差。

3. 调节信号发生器的频率，观察电压和电流的波形随频率变化的规律。

4. 断开交流电源，接入直流电源，观察电压和电流的波形，并测量其幅值和相位差。

5. 记录实验数据，并进行数据处理和分析。

实验结果。

通过实验观测和数据处理，得出以下结论：1. 在正弦稳态交流电路中，电压和电流的相量可以用复数表示，实部表示幅值，虚部表示相位差。

2. 电压和电流的相量之间存在幅值比和相位差的关系，符合正弦函数规律。

3. 频率对电压和电流的相量有影响，频率增大时，电压和电流的相量幅值减小，相位差增大。

4. 在直流电源下，电压和电流的相量均为实数，相位差为零。

实验分析。

通过本实验的研究，加深了对正弦稳态交流电路中相量的理解，验证了相关理论知识。

实验结果表明，电压和电流的相量在交流电路中具有一定的规律性，频率对相量也有一定的影响。

这对于进一步研究交流电路、分析电路性能具有一定的指导意义。

结论。

本实验通过对正弦稳态交流电路相量的研究，验证了电压和电流的相量在交流电路中的特性，加深了对相量概念的理解。

同时，实验结果对于进一步研究交流电路、分析电路性能具有一定的指导意义。

第 4 节正弦稳态电路的相量分析相量分析法相量分析法是针对正弦量激励下、且电路已进入稳态时的动态电路的分析。

因为电路在正弦量的激励下，各处的响应都是同频率的正弦量，因此，将电路的激励和响应都用相量来表示，把电阻、电感、电容元件用复数阻抗或复数导纳表示，将电路定律用相量形式表示，把时域电路转换成相量电路之后，描述动态电路的方程就由时域中的微分方程转换为频域中的复数代数方程，求解复数代数方程，求得各响应的相量，然后再将这些响应的相量转换成时域的正弦函数表达式。

相量分析法的步骤正弦量用相量表示，电阻、电感、电容元件用阻抗或导纳表示，画出相量电路；2 、相量电路中，用电阻电路的分析方法求解各响应的相量；3 、将求得的响应相量转换成时域的正弦函数表达式。

例 7.4-1 电路如图 7.4-1 （ a ）所示，已知，求 uS ， iL 和 ic 。

解：电流 iR 的相量为感抗容抗所以，得到相量电路如图 7.4-1 （ b ）所示。

图 7.4-1 （ b ）中，有则由 KCL 得由 KVL 得将相量再转换成正弦函数表达式，得例 7.4-2 电路如图 7.4-2 所示，已知，，电压源的角频率，求电流 i1 和 i2 。

解：用节点电压法求解，设节点 a 、 b 的节点电压分别是和，列写节点电压方程，节点 a ：节点 b ：代入参数并整理，得则，所以，因此，，例 7.4-3 电路如图 7.4-3 所示，已知电压源，求电流。

解：这是一个含有受控源的单回路电路，用相量法分析时，也可将受控源当独立源处理。

由 KVL 得，代入参数，得则一、有功功率无源二端网络 N 中含有线性电阻、电容、电感、受控源等元件，阻抗为。

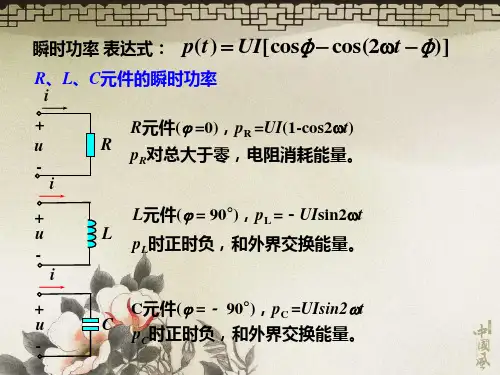
其端电压和端电流分别为。

二端网络 N 吸收的瞬时功率为平均功率（ average power ）是指在一个周期内吸收的瞬时功率的平均值，用 P 表示，即有功功率在一个周期内吸收的瞬时功率的平均值，称为平均功率，又称有功功率（ active power ），单位为瓦（ W ）。

G 2R 2 , R X
B 2 X 2 R X
1 | Y | , φ y φz |Z|
注
一般情况 G1/R B1/X。若Z为感性， X>0，则B<0，即仍为感性。
同样，若由Y变为Z，则有：
R
Y
G
jB
Z
jX
Y G jB | Y | φ y ,
Z R jX | Z | φz
1 . U U R U L UC R I jL I j I C
.
.
.
.
.
.
U 1 Z R jL j R jX Z z I C
Z— 复阻抗；R—电阻(阻抗的实部)；X—电抗(阻抗的虚部)； |Z|—复阻抗的模；z —阻抗角。 转换关系：
例
L + + uR - + uL u C -
i
R
已知：R=15, L=0.3mH, C=0.2F,
u 5 2 cos(t 60 )
+ uC -
f 3 104 Hz . 求 i, uR , uL , uC .
.
解
其相量模型为：
I
R
.
j L
.
U 560 V


jL j2 3 104 0.3 103 j56.5Ω 1 1 j j j26.5Ω 4 6 C 2π 3 10 0.2 10 1 15 j56.5 j26.5 33.5463.4o Ω Z R j L j C
（1）C > 1/L ，B>0， y>0，电路为容性，电流超前电压 相量图：选电压为参考向量， u 0

《电路分析》正弦稳态交流电路相量的研究实验报告一、实验目的1．研究正弦稳态交流电路中电压、电流相量之间的关系。

2. 掌握单相正弦交流电路中电压、电流及功率的测量方法3. 理解改善电路功率因数的意义并掌握其方法。

二、实验原理1. 在单相正弦交流电路中，用交流电流表测得各支路的电流值，用交流电压表测得回路各元件两端的电压值，它们之间的关系满足相量形式的基尔霍夫定律。

2. RC串联电路，在正弦稳态信号U的激励下，U R与U C 保持有90º的相位差，即当R阻值改变时，U R的相量轨迹是一个半园。

U、U C与U R三者形成一个直角形的电压三角形，如图4.1所示。

R值改变时，可改变φ角的大小，从而达到移相的目的。

图4.13. 在感性负载两端并联电容，可以改善电路的功率因数（cosφ值）。

三、实验平台NI Multisim 14.0四、实验步骤与数据记录、处理1. 单相交流电路的基尔霍夫电压定律按图4.2所示调用元件，连接电路。

将万用表均选为交流电压档，开启仿真开关，记录各万用表显示的数值至表格4-1中，并保留截图。

验证电压的相量关系，是否符合电压三角形。

表4-1 电压相量测量2、RLC交流参数测量按图4.3所示调用元件，建立RLC电路。

正确接入功率表，将万用表分别选为交流电压挡和交流电流挡，开启仿真开关，记录各仪表显示的数值至表格4-2中，并保留截图。

表4-2 RLC参数测量根据测量结果，计算RLC各参数，与实际值进行比较。

3、并联电路─电路功率因数的改善按图4.4所示调用元件，建立电路。

正确接入功率表，将万用表选为交流电流挡，开启仿真开关，记录各仪表显示的数值至表格4-3中。

改变电容的数值，记录各参数，观察功率因数的改变情况。

图4.4 功率因数改善电路表4-3 功率因数的改善五、实验结果总结1. 完成数据表格中的计算。

2. 根据实验数据，分别绘出电压、电流相量图，验证相量形式的基尔霍夫定律。

3. 画出功率因数随并联电容变化的曲线图。

依据上述数据，还可求出 依据上述数据，还可求出R1、L1： ：
& Us Z1 = = 38∠ 75 0 & I1 Z 1 = R 1 + j ωL 1 R 1 = 9.84 36.71 L1 = = 116.9mH 314
9-5
正弦稳态电路的功率 。 i u －。
＋
设一端口N内部不含独立源，仅有 、 、 设一端口 内部不含独立源，仅有R、L、C 内部不含独立源 吸收的功率： 吸收的功率：p=ui（关联方向） （关联方向） i = 2I cos(ωt + Ψi ) 设u = 2U cos(ωt + Ψu )
u
ϕ = Ψu − Ψi )
) − UIsin(-ϕ ) sin( 2ωt + 2Ψ ) = UI cos ϕ{1 + cos[2( ωt + Ψ ]} + UI sin ϕ sin[2(ωt + Ψ )]
u u
平均功率又称有功功率 一周期内的平均值 1T 1T p = ∫ pdt = ∫ UI[ cos ϕ + cos( 2ωt + Ψu + Ψi )]dt =UI cos ϕ T0 T0 功率因数 cosϕ用λ = cosϕ 无功功率 ϑ = UIsinϕ 视在功功率 S = UI
& 1 I I 导纳：阻抗Z的倒数定义为导纳 Y 的倒数定义为导纳： 导纳：阻抗 的倒数定义为导纳： = = = ∠ψ i − ψ u = Y ∠ϕ y & Z U U Y的代数式可写为： 的代数式可写为： 的代数式可写为 Y = G + jB ← 电纳 ↑ 电导 电阻YR =
单个元件的导纳： 单个元件的导纳：
单个元件的阻抗： 单个元件的阻抗：

Ue j ψ U ψ 相量的模=正弦量的有效值 U
相量辐角=正弦量的初相角
电压的有效值相量
目录 上页 下页 返回
或：
U e jψ U ψ Um m m
相量的模=正弦量的最大值 相量辐角=正弦量的初相角
注意:
电压的幅值相量
① 相量只是表示正弦量，而不等于正弦量。
i Imsin(ω t ψ ) = Ime
储能 放能 储能 放能
目录 上页 下页 返回
无功功率 Q 用以衡量电感电路中能量交换的规模。用瞬时 功率达到的最大值表征，即
p 瞬时功率 ： i u UI sin 2 ω t
U2 Q U I I XL
2
XL
单位：var
目录 上页 下页 返回
3.3.3 电容元件伏安关系相量形式
时域形式：
已知 i(t ) 2I sin( t i )
R
I
uR (t ) Ri (t ) 2RI sin( t i ) UR u 相量形式： 有效值关系：UR=RI I I 则
i
+

UR
R
U R RI i
相量关系：
相位关系u= i (u,i同相) UR=RI
U 1 落后于U 2
U2
U2
45 20
U1
+1
超前 U ？ 落后 1
目录 上页 下页 返回
3.3 基尔霍夫定律的相量形式
电阻元件伏安关系相量形式
电感元件伏安关系相量形式 电容元件伏安关系相量形式
目录 上页 下页 返回
3.3.1 电阻元件伏安关系相量形式
i(t) + uR(t)

. IL
2017年2月9日星期四
. U
16
9.1.3 阻抗（导纳）的串联和并联
1.阻抗的串联 . . . . U = Z1 I + Z2 I + · · · + Zn I . = (Z1+ Z2 + · · · + Zn) I . = ZI
Z=
n . I Z1 Z2 Zn
+ . U . I
k
∑ Z = ∑ (R + j X )
. I2 Y2
. In Yn
∑ Y = ∑ (G + j B )
k=1
k k
k=1
分流公式
Z1 Z2 两个阻抗Z1、Z2的并联等效阻抗为：Z = Z1 + Z2
2017年2月9日星期四 18
. Yk . Ik = I Y
+ . U -
Y
例：如图所示电路，已知R=10Ω, XL=10 Ω , XC=10 Ω, 求ab两端的等效阻抗Z；电压相量与电流相量相位差
2017年2月9日星期四 7
. . U = R + j X= | Z | j jwL R Z= . Z I . . I + + UR - + UL 1 X = XL - XC = wL. + . wC U UC X jZ = arctan R 讨论： 1 时， ①当 wL＞ wC 有 X＞0 ，jZ＞0
. UL
1 jwC
以电流为参考相量的相量图
. . UL + UC
. U
表现为电压超前电流，Z 呈感 性，称电路为感性电路。 满足：U 2 =UR2 + (UL-UC)2
2017年2月9日星期四