课件-第4章 正弦稳态电路分析--例题
- 格式:doc
- 大小:878.50 KB
- 文档页数:13





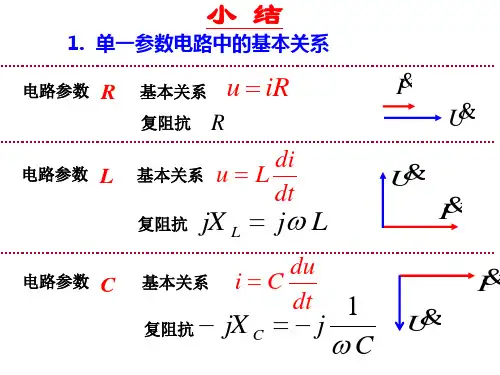




第4章 正弦稳态电路分析--例题√【例4.1】已知两个同频正弦电流分别为()A 3314cos 2101π+=t i ,()A 65314cos 2222π-=t i 。
求(1)21i i +;(2)dt di 1;(3)⎰dt i 2。
【解】 (1)设()i t I i i i ψω+=+=cos 221,其相量为i I I ψ∠=∙(待求),可得:()()()()A54.170314cos 224.14A54.17014.24A 34.205.14 A1105.19A j8.665 A15022A 601021︒-=︒-∠=--=--++=︒-∠+︒∠=+=∙∙t i j j I I I(2)求dtdi 1可直接用时域形式求解,也可以用相量求解()()︒+︒+=︒+⨯-=9060314cos 23140 60314sin 3142101t t dt di用相量形式求解,设dt di 1的相量为K K ψ∠,则有 )9060(31406010314K 1K ︒+︒∠=︒∠⨯==∠∙j I j ωψ两者结果相同。
(3)⎰dt i 2的相量为︒∠=︒∠︒-∠=∙12007.0903********ωj I【例4.2】 图4-9所示电路中的仪表为交流电流表,其仪表所指示的读数为电流的有效值,其中电流表A 1的读数为5 A ,电流表A 2的读数为20 A ,电流表A 3的读数为25 A 。
求电流表A 和A 4的读数。
图4-9 例4.2图【解】 图中各交流电流表的读数就是仪表所在支路的电流相量的模(有效值)。
显然,如果选择并联支路的电压相量为参考相量,即令V 0︒∠=∙S S U U ,根据元件的VCR 就能很方便地确定这些并联支路中电流的相量。
它们分别为:A 25 ,A 20 ,A 05321j I j I I =-=︒∠= 根据KCL ,有:()A095A 5A 457.07A 55324321︒∠==+=︒∠=+=++=j I I I j I I I I 所求电流表的读数为:表A :7.07 A ;表A 4:5 A【例4.3】 RLC 串联电路如图4-12所示,其中R =15Ω,L =12mH ,C =5μF ,端电压u =1002cos (5000t )V 。
试求:电路中的电流i (瞬时表达式)和各元件的电压相量。
Cj ω1___∙∙∙图4-12 例4.3题图【解】 用相量法求解时,可先写出已知相量和设定待求相量,本例已知L R U U I V U、、, 0100∠=∙和∙CU 为待求相量,如图所示。
然后计算各部分阻抗:A A Z U I j Z Z Z Z j CjZ j L j Z eq c L R eqcL R ︒-∠=︒∠︒∠==Ω︒∠=Ω+=++=Ω-=-=Ω==Ω=13.53413.5325010013.5325)2015(4016015Z ωω 各元件电压相量为:V I Cj U V I L j U V I R U CLR︒-∠=-=︒∠==︒-∠==13.143160187.3624013.5360 ωω正弦电流i 为A t i )13.535000cos(24︒-=注意:本例中有U U U U C L >>,。
(思考:如果本例的电源频率可变,则等效阻抗)(Z ωj eq 会不会变为容性阻抗或电阻性阻抗?)【例4.4】 画出例4.3电路(图4-12所示电路)的相量图。
【解】 该电路为串联电路,可以相对于电流相量I 为参考,根据CL R U U U U ++=,画出电压相量组成的多边形。
画法如下。
由于串联电路中每个元件流过同一电流I ,所以可以先画出电流I 的相量,然后再根据各个元件上电压电流关系画出各自的电压相量,最后根据KVL ,画出端口电压U的相量,如图4-13所示。
各相量位置 相量相加(平移叠加) 图4-13 例题4.3题相量图【例4.5】 图4-14所示电路中的独立电源全部都是同频正弦量,试列出该电路结点电压方程和回路方程。
∙s U ∙_5∙U图4-14 例4.5题图【解】 如图取参考结点,则该电路的结点1、结点2电压方程为:533243133311231321)()(s s n n s s n n I U Y U Y Y U Y U Y U Y U Y U Y Y Y ∙∙∙∙∙∙∙∙+-=++-+=-++对于回路电流方程,如取顺时针方向的回路电流为21l l I I ∙∙、和3l I ∙(见图)为电路变量,则有:53354243342432121221210)()()(s l l l s l l l s l l I I U I Z Z I Z U I Z I Z Z Z I Z U I Z I Z Z ∙∙∙∙∙∙∙∙∙∙∙∙-==+++--=-+++-=-+【例4.6】 图4-15所示电路中,已知()V t u s ︒+=60314cos 2200,电流表A 的读数为2A ,电压表V 1、V 2的读数均为200V 。
求参数R 、L 、C ,并作出该电路的相量图。
图4-15 例4.6题图【解】 根据题意可设:V U s︒∠=60200 (已知),i I φ∠=2 A ,11200φ∠=U V ,22200φ∠=U V ,根据图4-15电路,可列写如下电压、电流关系和电路方程: ()()()i i L j R IUZ IU C j KVL φφωφφωφφ-∠=+==-∠==-∠+∠=︒∠1112221100100120020060200 依次求解上列方程,取一组合理解为:HL R F C i 159.06.8685.3190012021=Ω==︒=︒=︒=μφφφ运用相量图:已知:V U s ︒∠=60200 ,且U 1=U 2=200V ,21U U U s +=,所以三个电压的相量一定构成一个正三角形(有两个可能的正三角形)。
由于C Z Z Z +=1,流过同一电流,但电压幅值相等,所以有:C Z Z Z ==1,三个阻抗也一定构成一个正三角形。
取一个合理的可能,如图4-16所示。
1Z图4-16,例4.6题的相量图 根据该相量图可得:⎪⎩⎪⎨⎧Ω+=Ω︒∠=Ω-=Ω︒-∠=Ω-=Ω︒-∠=506.8630100506.8630100100901001j Z j Z j Z C , 所以, ⎪⎪⎩⎪⎪⎨⎧Ω=Ω=Ω=50,10016.86L C R ωω 得: ⎪⎪⎩⎪⎪⎨⎧===⨯=H L F C 159.03145085.313141001μ√【例4.7】 图4-17(a )中正弦电压50Hz 380==f V U s ,,电容可调,当F C μ95.80=时电流表A 的读数最小,其值为2.59A 。
求图中电流表A 1的读数。
1s U ∙(a)(b )图4-17 例4.7题图【解】 方法一:当I 最小时,表示电路的输入导纳最小(或者阻抗最大),有 111L j R C j Y ωω++=当C 变化时,只改变Y 的虚部,导纳最小意味着虚部为零,∙∙I U s 与同相位。
设V 0380︒∠=∙s U ,则︒∠=∙059.2I ,而A j U C j I s C 66.9==∙∙ω,设,111φ∠=∙I I 则根据KCL 有1166.9059.2φ∠+=︒∠I j所以: ⎩⎨⎧=-=59.2cos 66.9sin 1111φφI I解得:AA I 10cos /59.27559.266.9arctan 111==︒-=⎪⎭⎫⎝⎛-=φφ 故电流表1A 的读数为10A 。
根据以上数据,还可以求得参数1R 和L 1,即 Ω︒∠==∙∙753811I U Z s故: Ω=84.91RmH H L 9.11631471.361==方法二:运用相量图:由于是感性支路,1I 始终滞后s U 一个角度,C I 始终超前sU 90°,所以可先定性画出电路的相量图,如图4-17(b )。
当电容C 变化时,电流1I 始终不变,只改变C I 的大小。
由于C I I I +=1,所以,三个电流相量组成一个三角形。
由相量图可看出,只有C I 变化到使得I 和sU 平行且重合时,电流I 才最小。
此时,I 和sU 同相位,三个电流相量组成直角三角形。
此时,A CU I s C 66.93801095.803146=⨯⨯⨯==-ω, I =2.59 A所以电流表A 1的读数为:A 1066.959.222221=+=+=CI I I【例4.8】 图4-20电路是测量电感线圈参数R 、L 的实验电路,已知电压表的读数为50V ,电流表的读数为1A ,功率表的读数为30W ,电源的频率f =50Hz 。
试求R 、L 的值。
图4-20 例4.8题图【解】 根据图中3个表的读数,可以先求出线圈的阻抗:Ω==+=∠=50IUZ Lj R Z Z ωϕ由 ︒=⎪⎭⎫⎝⎛==13.5330arccos 30cos UI UI ϕϕ得: 解得:m HL R j Z 12716.314404030)4030(13.5350===Ω=Ω+=Ω︒∠=ω另外一种方法是利用功率表的读数表示电阻吸收的有功功率,即 302==R I P得: Ω=30R 而(),22Z L R ω+= 故可求得Ω=Ω-=40305022L ω,所以 mH ωL 1273144040===。
【例4.9】 求例4-8电路中线圈吸收的复功率S 。
【解】 根据电压、电流相量就可以计算复功率。
令A I V U︒-∠=︒∠=13.531050 ,则, 有 S VA j A V I U)4030(13.53 1050*+=︒∠⋅︒∠== 或者 VA j Z I S )4030(2+==。
可见线圈吸收有功功率30W ,吸收无功功率40Var 。
【例4.10】 图4-21(a )所示电路,外加50HZ 、380V 的正弦电压,感性负载吸收的功率kW P 201=,功率因数6.01=λ。
若要使电路的功率因数提高到9.0=λ,求在负载的两端应并联的电容值(图中虚线所示)。
图4-21 例4.10题图【解】方法一并联电容C 不会影响支路1的复功率(设为S ),因为1∙∙I U 和都没有改变。
但是并联电容后,电容发出的无功功率“补偿”了电感L 吸收的无功功率,减少了电源提供的无功功率,从而提高了电路的功率因数。
并联电容C 前后补偿无功功率的关系如图4-10(b )所示。
设并联电容电路吸收的复功率为S 。
电容吸收的复功率为C S ,则有并联电容前有:kVAj jQ P S k P Q kW P )67.2620(var 67.26tan 2013.53cos 1111111111+=+====︒==ϕϕϕλ,,并联电容后要求︒±===84.259.0cos 9.0ϕϕλ,,即,而有功功率没有变,故kVAj jQ P S k P Q )69.920(var69.9tan 11±=+=±==ϕ故电容的复功率var)36.36var(98.16j 1k j k S S S C--=-=或显然取较小的电容为好,ωC U Y U I U S CCCCC C22===** ,故有()uF F C 49.3743803141098.1623=⨯⨯=方法一中,并联电容前后的复功率中,有功功率并没有变化,变化的只是无功功率,所以也可以只计算将功率因数补偿到0.9时需要电容提供的无功功率来计算电容值。