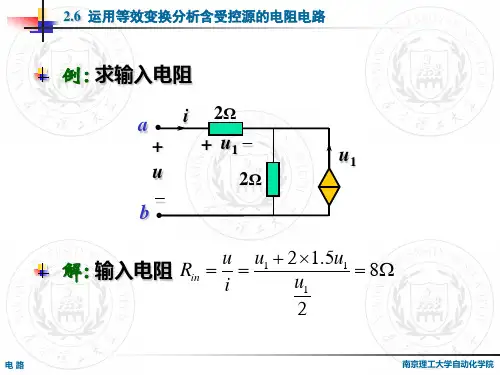
含受控源电路分析和习题课
- 格式:ppt
- 大小:1.63 MB
- 文档页数:43

电路分析中含受控源的电路分析含有受控源的电路分析是电路分析中的一种重要方法,用于分析电路中存在各类受控源的电路。
受控源是一种与输入信号有关的电源,它的电压或电流与电路中的一些参数有关。
常见的受控源有电压受控电压源(VCVS)、电流受控电流源(CCCS)、电流受控电压源(CCVS)和电压受控电流源(VCIS)等。
在含有受控源的电路分析中,首先需要建立电路的拓扑结构和元件的数学模型。
然后,根据电路中各个元件之间的连接关系和电路定律,可以列写出电路的基尔霍夫方程。
而对于含有受控源的电路分析,还需要考虑受控源的特性和输入信号的影响。
以电压受控电压源(VCVS)为例,电路中的一个元件可以认为是一个电流与输入电压之间存在关系的受控源。
在分析电路时,可以使用残源法、节点电压法或混合法等方法。
其中,节点电压法是最为常用的方法之一在节点电压法中,首先需要选择一个参考节点,并以该节点为基准确定其他节点的电压。
然后根据电压源、电压受控源和电流源等的性质,可以得到各个节点的电压与输入信号之间的关系。
在分析电路时,可以运用Kirchhoff定律、欧姆定律和元件电压-电流特性等基本原理,通过建立节点方程,将电路进行简化和分析。
受控源的特性对电路的分析和计算产生了影响。
在分析过程中,需要根据受控源的电压或电流与输入信号的关系,将其转换为等效电源。
例如,可以通过电流受控电流源(CCCS)将电压源转换为等效的电流源。
通过受控源的转换和简化,可以将电路分析问题转换为求解一组线性方程的问题。
通过受控源的电路分析,可以获得电路中各个节点的电压、元件的电流以及功率等信息。
这对于电路设计、电路故障分析等都具有重大的意义。
通过电路分析,可以评估电路的性能,确定电路中的瓶颈和关键元件,并改进电路的设计。
总而言之,含有受控源的电路分析是电路分析中一种重要的方法。
通过建立电路模型、使用电路定律和数学方法,可以对含有受控源的电路进行分析和计算。
通过受控源的转换和简化,可以将电路分析问题转化为线性方程组的求解问题,从而得到电路中各个节点的电压、元件的电流以及功率等信息。

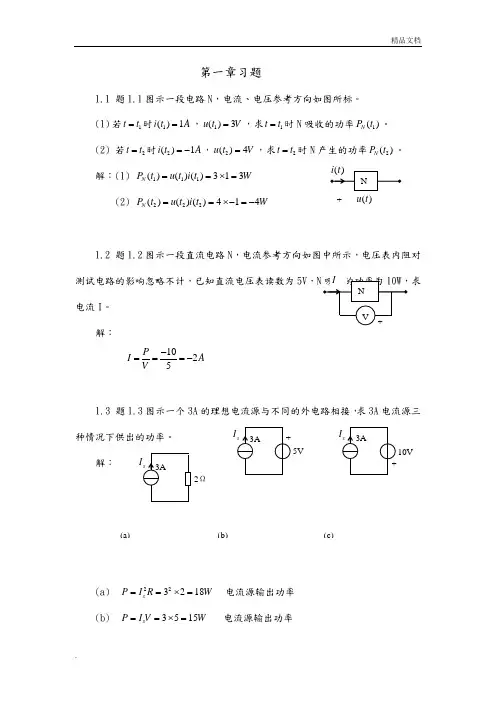
第一章习题1.1 题1.1图示一段电路N ,电流、电压参考方向如图所标。
(1) 若1t t =时1()1i t A =,1()3u t V =,求1t t =时N 吸收的功率1()N P t 。
(2) 若2t t =时2()1i t A =-,2()4u t V =,求2t t =时N()P t 解:(1) 111()()()313N P t ut i t W ==⨯= (2) 222()()()414N P t u t i t W ==⨯-=-1.2 题1.2图示一段直流电路N ,电流参考方向如图中所示,电压表内阻对测试电路的影响忽略不计,已知直流电压表读数为5V ,电流I 。
解: 1025P I A V -===-1.3 题1.3图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三种情况下供出的功率。
解:(a) 223218s P I R W ==⨯= 电流源输出功率 (b) 3515s P I V W ==⨯= 电流源输出功率(c) 31030s P I V W ==⨯-=- 电流源吸收功率1.4 题1.4图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
解:流过3Ω电阻的电流为 12A+6A=18A 流过12Ω电阻的电流为 18A-15A=3A 流过电阻R 的电流为 3A-12A-5A=-14A 可得: I=-14A+15A=1A 18331290S U V =⨯+⨯= 1511231.514R ⨯-⨯==Ω-1.5 题1.5图示电路,已知U=28V ,求电阻R 。
解:根据电源等效,从电阻R 两端 可等效为如下图等效电路。
有: '41515442I A =⨯=+ '448R =Ω+Ω=Ω可得: '287152828U R U I R ===Ω--1.6 求题1.6图示各电路的开路电压。
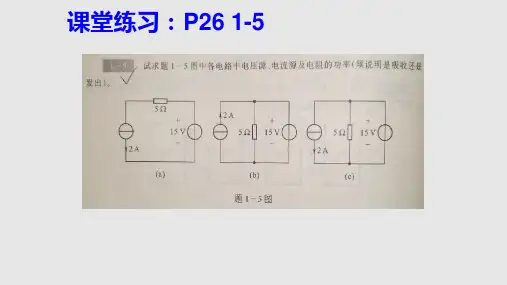
解:(a) 2010530OC U V A V =-⨯Ω=-(b) 开路时,流过8Ω电阻的电流为 931189A ⨯=+ 流过6Ω电阻的电流为 1832189A ⨯=+可得: 26184OC U V =⨯-⨯=(c) 开路时,8Ω电阻的电压为 8208128V ⨯=+ 2Ω电阻的电压为 5210A V ⨯Ω= 可得: 82100OC U V V V V =+-=1.7 求题1.7图示各电路的电流解:(a) 6242I A +== (b) 201610221I A --==-+(c) 将电压源等效为电流源,如右图示 显然 0I =(d) 电压源供出的总电流为: 2121313//612//6124I A ===++++根据分流关系,流过3Ω电阻的电流为 63236A ⨯=+流过12Ω电阻的电流为 631126A ⨯=+可得: 211I A A A =-=1.8求题1.8图示各电路的电压U 。


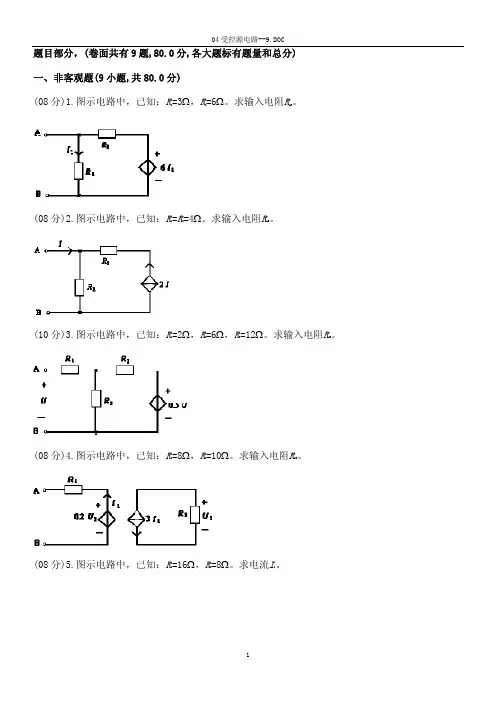
题目部分,(卷面共有9题,80.0分,各大题标有题量和总分)一、非客观题(9小题,共80.0分)(08分)1.图示电路中,已知:R1=3Ω,R2=6Ω。
求输入电阻R AB。
(08分)2.图示电路中,已知:R1=R2=4Ω。
求输入电阻R AB。
(10分)3.图示电路中,已知:R1=2Ω,R2=6Ω,R3=12Ω。
求输入电阻R AB。
(08分)4.图示电路中,已知:R1=8Ω,R2=10Ω。
求输入电阻R AB。
(08分)5.图示电路中,已知:R1=16Ω,R2=8Ω。
求电流I1。
(08分)6.图示电路中,已知:R1=4Ω,R2=10Ω。
求电流I。
(10分)7.图示电路中,已知:R1=4Ω,R2=8Ω,R3=6Ω。
求电压U1。
(10分)8.图示电路中,已知:R1=4Ω,R2=6Ω,R3=8Ω。
求电压U2。
(10分)9.图示电路中,已知:R1=12Ω,R2=6Ω。
求电流源的端电压U。
答案部分,(卷面共有9题,80.0分,各大题标有题量和总分)一、非客观题(9小题,共80.0分)(08分)1.答案如图示,外加电压U,则产生电流I。
则输入电阻:代入I1,I2得:R AB=6Ω(08分)2.答案如图示,外加电压U,则产生电流I。
I=I1-2I则输入电阻:(10分)3.答案如图示,外加电压U,则产生电流I1。
输入电阻:(08分)4.答案如图示,外加电压U。
U=-R1I1+0.2U2U2=-3R2I1代入U2得:U=-14I1输入电阻(08分)5.答案R1=2R2则I2=2I1I S=5I1+I2+I1=8I112=8I1I1=1.5A(08分)6.答案U-2U1=(R1+R2)IU1=-R1I代入U1得:U=6I12=6II=2A(10分)7.答案U1=R1I1代入I1得:3U1=U1+20U1=10V (10分)8.答案0.4U2=9.6U2=24V(10分)9.答案由原电路得:U S=R1I1+10I1+UU=20V。


文章编号:JL 010229(2006)03000502运用戴维南定理对含受控源电路的求解及分析李 光(石家庄铁道学院四方学院,河北石家庄050228) 摘 要:本文通过对《电路》教材中含有受控源电路的求解,着重分析了受控源的电源性质及戴维南定理在处理电路过程中的应用。
关键词:受控源;戴维南定理;电源性质;控制量转移 中图分类号:TN 7 文献标识码:A1 问题引出在现行电路教材中,对含有受控源的线性电路网络用戴维南定理分析时,即在求戴维南等效电路的电压源和内阻抗时,只允许把受控源视为电阻性元件保留在电路中,对电路进行分析简化,那么,能否利用受控源的电源性,将其作为独立源来处理简化电路呢?例题:电路如图(a )所示,试用戴维南定理求电路中电流I 和流过3V 电压源电流I 1。
解:把受控源分别视为电阻性和电源性元件求解。
解法1:将受控源视为电阻性元件,断开3V 电压源支路,应用戴维南定理进行求解。
断开3V 电压源支路如图(b )所示,求ab 端收稿日期:20051221责任编辑:姚树琪校 对:王素娟作者简介:李光(1977-),男,汉族,河北深州人,电气工程系,讲师,主要从事电工电子学教学与研究。
口开路电压U oc ,可求得I =0.5AU oc =3V将ab 端口短路如图(c )所示,求短路电流Isc 得I sc =0.5A故可求得戴维南等效电阻R o =U ocI sc=6Ψ则戴维南等效电路如图(d )所示,可求得I 1=3+36=1A返回原电路图(a ),由KV L 得 2006年9月 石家庄联合技术职业学院学术研究 Sept .2006 第1卷第3期 Academic Research o f Shijiazhuang Lionful Vo ca tional College Vo l .1No .3 3I 1-3-6I =0则有I =0A解法2:将受控源视为独立源,断开3V 电压源支路如图(b )。
用戴维南定理分析含受控源电路的两种求解方法戴维南定理是一种用于求解包含受控源电路的方法,可以用来简化电路分析过程。
它基于两个重要的原理:戴维南定理一和戴维南定理二、在本文中,将分析使用戴维南定理解决含有受控源电路的两种方法。
第一种方法是直接应用戴维南定理。
这种方法的核心思想是将受控源看作是独立的源,然后使用戴维南定理对电路进行分析。
具体步骤如下:1.将受控源替换为一个等效的独立源,其大小由受控元件的传输函数决定。
2.对电路进行划分,将分析对象划分为两个不同的部分:一个是受控源所控制的部分,另一个是受控源所控制的部分。
3.对两个部分分别应用戴维南定理进行分析。
对于受控源所控制的部分,把受控源替换为等效独立源,并求解得到电流或电压。
对于受控源所控制的部分,保持原样进行分析。
4.最后,根据受控源的传输函数,利用以上步骤中得到的结果计算出受控源的电流或电压。
这种方法的优点是能够直接应用戴维南定理进行分析,简化了原电路的复杂性。
但是,该方法的缺点是需要进行额外的计算来确定受控源的等效独立源。
第二种方法是使用戴维南定理的回路剪切法。
该方法是将受控源的作用进行回路剪切,然后通过引入未知变量进行分析。
具体步骤如下:1.对电路中的其中一回路进行剪切,将受控源切断。
2.在切断处引入未知变量,例如电流或电压。
3.根据戴维南定理,建立剪切处的电压或电流方程,利用已知条件进行求解。
4.利用未知变量的值,通过受控源的传输函数计算出受控源的电流或电压。
5.重复以上步骤,对每一个回路进行剪切,建立方程并解析。
这种方法的优点是可以直接应用戴维南定理,同时通过引入未知变量对电路进行分析。
而缺点是需要进行多次剪切和建立方程的过程,会增加计算的复杂性。
综上所述,戴维南定理是一种用于分析含有受控源电路的有效方法。
根据具体的电路情况和分析需求,可以选择直接应用戴维南定理或使用回路剪切法进行分析。
无论采用哪种方法,戴维南定理都能够简化电路分析过程,提高分析效率。