第4章_受控源电路的分析方法
- 格式:ppt
- 大小:910.50 KB
- 文档页数:32

电路分析中含受控源的电路分析含有受控源的电路分析是电路分析中的一种重要方法,用于分析电路中存在各类受控源的电路。
受控源是一种与输入信号有关的电源,它的电压或电流与电路中的一些参数有关。
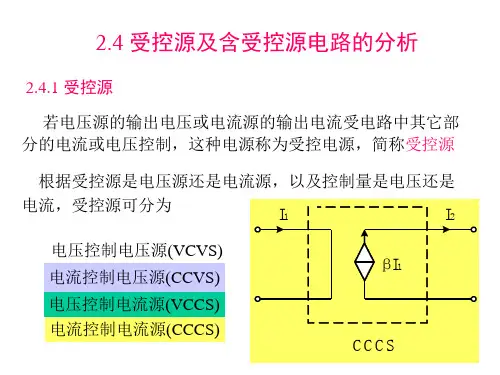
常见的受控源有电压受控电压源(VCVS)、电流受控电流源(CCCS)、电流受控电压源(CCVS)和电压受控电流源(VCIS)等。
在含有受控源的电路分析中,首先需要建立电路的拓扑结构和元件的数学模型。
然后,根据电路中各个元件之间的连接关系和电路定律,可以列写出电路的基尔霍夫方程。
而对于含有受控源的电路分析,还需要考虑受控源的特性和输入信号的影响。
以电压受控电压源(VCVS)为例,电路中的一个元件可以认为是一个电流与输入电压之间存在关系的受控源。
在分析电路时,可以使用残源法、节点电压法或混合法等方法。
其中,节点电压法是最为常用的方法之一在节点电压法中,首先需要选择一个参考节点,并以该节点为基准确定其他节点的电压。
然后根据电压源、电压受控源和电流源等的性质,可以得到各个节点的电压与输入信号之间的关系。
在分析电路时,可以运用Kirchhoff定律、欧姆定律和元件电压-电流特性等基本原理,通过建立节点方程,将电路进行简化和分析。
受控源的特性对电路的分析和计算产生了影响。
在分析过程中,需要根据受控源的电压或电流与输入信号的关系,将其转换为等效电源。
例如,可以通过电流受控电流源(CCCS)将电压源转换为等效的电流源。
通过受控源的转换和简化,可以将电路分析问题转换为求解一组线性方程的问题。
通过受控源的电路分析,可以获得电路中各个节点的电压、元件的电流以及功率等信息。
这对于电路设计、电路故障分析等都具有重大的意义。
通过电路分析,可以评估电路的性能,确定电路中的瓶颈和关键元件,并改进电路的设计。
总而言之,含有受控源的电路分析是电路分析中一种重要的方法。
通过建立电路模型、使用电路定律和数学方法,可以对含有受控源的电路进行分析和计算。
通过受控源的转换和简化,可以将电路分析问题转化为线性方程组的求解问题,从而得到电路中各个节点的电压、元件的电流以及功率等信息。





受控源电路分析电子电路学是电子信息类专业中的一门重要课程,其中受控源电路是电子电路学中的重要内容之一。
本文将对受控源电路进行深入分析,包括基本原理、常见电路的特点与应用等。
一、基本原理受控源电路是指通过对电流或电压的控制来控制电路中其他元件的电流或电压的电路。
在受控源电路中,常见的受控源有电流控制电压源(CCVS)、电压控制电流源(VCIS)、电流控制电流源(CCCS)和电压控制电压源(VCVS)。
1. 电流控制电压源(CCVS):受控电路中的电流可以通过外部电路对其电压进行控制。
例如,一个三端元件可以通过控制其两个端口之间的电压来控制其第三个端口的电流。
2. 电压控制电流源(VCIS):受控电路中的电流可以通过外部电路对其电压进行控制。
与CCVS相反,VCIS允许通过控制电压来控制其他器件中的电流。
3. 电流控制电流源(CCCS):受控电路中的电流可以通过外部电路对其电流进行控制。
换句话说,通过调整受控电路中的电流,可以控制其他元件中的电流。
4. 电压控制电压源(VCVS):受控电路中的电压可以通过外部电路对其电压进行控制。
与CCCS相反,VCVS允许通过控制电压来控制其他元件中的电压。
二、常见电路的特点与应用1. 压控振荡器(VCO)电路压控振荡器是一种特殊的受控源电路,其输出频率可以通过输入电压的变化来控制。
VCO电路在无线通信系统及频率合成器中得到广泛应用,能够生成可调节的信号频率。
2. 差分放大器电路差分放大器由两个受控源电路构成,其输入信号分别作用于两个输入端口,输出为两个输入之差的放大倍数。
差分放大器用于信号处理、滤波和增益放大等应用。
3. 运算放大器电路运算放大器(Op-Amp)是一种常用的受控源电路,具有高增益、高输入阻抗和低输出阻抗等特点。
它在模拟电路中被广泛用于信号放大、滤波、积分和微分等应用。
4. 电流镜电路电流镜是一种利用受控源电路实现电流复制功能的电路。
通过调整镜像电流源的电流大小,可以达到对电流进行精确复制的目的。


受控源的电路分析电信132班33张世东【实验目的】1.了解用运算放大器组成四种类型受控源(VCVS、VCCS、CCVS、CCCS)的线路原理2.测试受控源转移特性及负载特性【实验设备和材料】1.计算机及Mulitisim7.0电子仿真软件。
2.KHDL-1型电路实验箱。
3.MF-500型万用表,数字万用表。
【实验原理】VCVSU1 + _2+__+U1VCCS(a) (b)CCVS_+U2CCCS(c) (d)(1)压控电压源(VCVS)如图1所示U1+_图1由于运放的输入“虚短”路特性,即 1u u u n p == 所以有 2122R u R u i n == 又因运放内阻为∞,有21i i = 因此121212121222112)1()()(u R R R R R u R R i R i R i u +=+=+=+= 即运放的输出电压2u 只受输入电压1u 的控制而与负载L R 大小无关,电路模型如图(a )所示。
转移电压比21121R Ru u +==μ μ为无量纲,又称为电压放大系数。
这里的输入、输出有公共接地点,这种联接方式称为共地联接。
(2)压控电流源(VCCS ) 将图2的1R 看成一个负载电阻L R ,如图2所示,即成为压控电流源VCCS 。
U 1U 2+_+_图2此时,运放的输出电流 Ru R u i i n R L 1===。
即运放的输出电流L i 只受输入电压1u 的控制,与负载L R 大小无关。
电路模型如图(b )所示。
转移电导 )(11s Ru i g L m ==这里的输入、输出无公共接地点,这种联接方式称为浮地联接 (3) 流控电压源(CCVS ) 如图3所示由于运放的“+”端接地,所以0=p u ,“—”端电压n u 也为零,此时运放的“—”端称为虚接地点。
显然,流过电阻R 的电流1i 就等于网络的输入电流S i 。
此时,运放的输出电压R i i u S R -=-=12,即输出电压2u 只受输入电流S i 的控制,与负载L R 大小无关,电路模型如图(c )所示。
用戴维南定理分析含受控源电路的两种求解
方法
1含受控源电路
受控源电路,也称为变编电路,是由一个特定的器件或元件组成的电路,该器件或元件可以以普通的电路元件不能做到的方式影响信号,因此用作控制的源。
根据含受控源电路的求解方法,可分为戴维南定理求解和微分格式求解。
2戴维南定理求解
戴维南定理是瞬态稳态及其他复杂电路求解最有效的工具,既可用于复杂又可用于简单的电路分析。
它可以用于求解含受控源电路的结构,是一种相当有用的方法。
戴维南定理求解含受控源电路的步骤如下:第一步,从源电路中提取出受控源;第二步,用一个普通的电源代替受控源,测量受控源的输出电压;第三步,将受控源替换成正确参数的模型,并利用电路分析计算其输出电压,比较得到受控源的正确参数。
3微分格式求解
微分格式求解可以用于求解大型以及复杂的含受控源电路,它的优点是可以减少解的复杂度,从而提高求解的效率。
微分格式求解含受控源电路的步骤如下:将受控源电路转换为微分格式,根据求解时间分离出受控源的瞬态响应;利用瞬态响应的特定解决方案求出单个
节点上的受控源输入幅度;根据受控源感性参数反推出受控源的参数;最后,把受控源替换成正确参数的模型,并用在受控源代替原电路形式实现完整的电路模拟。
4总结
使用戴维南定理可以有效求解含受控源电路,目前常用的两种方法是戴维南定理求解和微分格式求解,比较简单、容易理解易于使用。
另外,其他如牛顿-拉弗森定理、传统方程法等求解方法也可以求解含受控源电路。
用戴维南定理分析含受控源电路的两种求解方法戴维南定理是一种用于求解包含受控源电路的方法,可以用来简化电路分析过程。
它基于两个重要的原理:戴维南定理一和戴维南定理二、在本文中,将分析使用戴维南定理解决含有受控源电路的两种方法。
第一种方法是直接应用戴维南定理。
这种方法的核心思想是将受控源看作是独立的源,然后使用戴维南定理对电路进行分析。
具体步骤如下:1.将受控源替换为一个等效的独立源,其大小由受控元件的传输函数决定。
2.对电路进行划分,将分析对象划分为两个不同的部分:一个是受控源所控制的部分,另一个是受控源所控制的部分。
3.对两个部分分别应用戴维南定理进行分析。
对于受控源所控制的部分,把受控源替换为等效独立源,并求解得到电流或电压。
对于受控源所控制的部分,保持原样进行分析。
4.最后,根据受控源的传输函数,利用以上步骤中得到的结果计算出受控源的电流或电压。
这种方法的优点是能够直接应用戴维南定理进行分析,简化了原电路的复杂性。
但是,该方法的缺点是需要进行额外的计算来确定受控源的等效独立源。
第二种方法是使用戴维南定理的回路剪切法。
该方法是将受控源的作用进行回路剪切,然后通过引入未知变量进行分析。
具体步骤如下:1.对电路中的其中一回路进行剪切,将受控源切断。
2.在切断处引入未知变量,例如电流或电压。
3.根据戴维南定理,建立剪切处的电压或电流方程,利用已知条件进行求解。
4.利用未知变量的值,通过受控源的传输函数计算出受控源的电流或电压。
5.重复以上步骤,对每一个回路进行剪切,建立方程并解析。
这种方法的优点是可以直接应用戴维南定理,同时通过引入未知变量对电路进行分析。
而缺点是需要进行多次剪切和建立方程的过程,会增加计算的复杂性。
综上所述,戴维南定理是一种用于分析含有受控源电路的有效方法。
根据具体的电路情况和分析需求,可以选择直接应用戴维南定理或使用回路剪切法进行分析。
无论采用哪种方法,戴维南定理都能够简化电路分析过程,提高分析效率。