实验标准和平均值

化学分析中的精确度和准确度在化学分析领域中，精确度和准确度是两个非常重要的概念。

精确度指的是分析结果的稳定性和重现性，而准确度则表示结果与真实值之间的接近程度。

在进行化学实验和分析过程中，确保精确度和准确度是保证结果可靠性和数据有效性的关键。

I. 精确度的定义和评估精确度是指在一系列重复试验或测量中，结果的接近程度。

它反映了实验的准确程度和数据的稳定性。

为了评估分析的精确度，可以采用以下几种方法：1. 重复性：进行多次实验或测量，比较结果的变化范围。

如果结果之间的差异较小，则说明实验的重复性较好，具有较高的精确度。

2. 平均值和标准偏差：计算多次实验或测量的平均值和标准偏差。

平均值反映了数据的集中趋势，而标准偏差表示数据的离散程度。

较小的标准偏差意味着较高的精确度。

3. 控制样品：使用已知浓度的控制样品进行重复测量。

通过比较测量结果和真实值之间的差异来评估精确度。

II. 准确度的定义和评估准确度是指分析结果与真实值之间的接近程度。

在化学分析中，确定分析方法的准确度十分重要，特别是在质量控制和质量保证方面。

准确度评估的方法包括：1. 标准品测定：使用已知浓度的标准品进行测定，并比较结果与真实值之间的差异。

较接近真实值的结果表示准确度较高。

2. 加标回收率：向待测样品中加入已知浓度的标准品，再进行测定。

通过计算样品中标准品回收的百分比，评估准确度。

3. 外部验证：将分析结果与其他实验室或方法进行比较，以确定准确度。

与其他结果相一致的结果具有较高的准确度。

III. 精确度和准确度的重要性精确度和准确度是保证化学分析结果可靠性的关键因素。

只有进行精确度的控制，才能确保实验数据的可重复性和稳定性。

而准确度的控制则保证了实验结果与真实值之间的接近程度。

准确的分析结果对于科学研究、质量控制、环境监测等领域至关重要。

它们直接影响到决策的准确性和过程的可控性。

例如，在药物研发中，仅有准确的分析结果才能确保药物的有效性和安全性。

橡胶热老化试验标准警告:使用本标准的人员应熟悉正规实验室操作规程。

本标准无意涉及因使用本标准可能出现的所有安全问题。

制定相应的安全和健康制度并确保符合国家法规是使用者的责任。

1 范围本标准适用于硫化橡胶或热塑性橡胶在常压下进行热空气加速老化和耐热试验。

2 引用标准下列标准所包含的条文，通过在本标准中引用而构成为本标准的条文。

本标准出版时，所示版本均为有效。

所有标准都会被修订，使用本标准的各标准的各方应探讨使用下列标准最新版本的可能性。

GB/T 2941-1991橡胶试样环境调节和试验的标准温度、湿度及时间(eqv ISO 471:1983)GB/T 9865.1-1996硫化橡胶或热塑性橡胶样品和试样的制备第一部分物理试验(idt ISO 4661-1:1993)GB/T 14838-1993 橡胶与橡胶制品试验方法标准精密度的确定(neq ISO/TR 9272:1986)3 原理试样在高温和大气压力下的空气中老化后测定其性能，并与未老化试样的性能作比较。

与使用权有关的物理性能应用来判定老化程度，介在没有这些性能的确切鉴定的情况下，建议测定拉伸强度、定伸应力、拉断伸长率和硬度。

3.1 热空气加速老化在本试验方法中，氧气浓度很低，即使氧化作用很快，氧气也无法充分扩散到橡胶内部以保持一致的氧化作用。

因此，在标准试验方法中规定的厚度的样品适合于本试验方法使用时，本老化试验方法对老化性能差的橡胶可能得出错误的结果。

3.2 耐热试验在本试验方法中，试样经受与使用时间相同温度和规定时间后，测定适当的性能，并与未老化试样的性能作比较。

4 试验装置橡胶试样采用热空气老化箱进行试验，老化箱应符合下列要求:a)具有强制空气循环装置，空气流速0.5m/s,1.5m/s,试样的最小表面积正对气流以避免干扰空气流速;b)老化箱的尺寸大小应满足样品的总体积不超过老化箱有效容积的10%，悬挂试样的间距至少中华人民共和国国家质量监督检验检疫总局2001-08-28批准 2002-05-01实施为10?，试样与老化箱壁至少相距50?;C)必须有温度控制装置，保证试样的温度保持在规定的试验温度的公差范围内;d)加热室内有测温装置记录实际加热温度;e)在加热室结构中不得使用钢或铜合金;f)老化箱的空气置换次数为每小时三到十次;g)空气进入老化箱前应加热到老化箱规定的试验温度的公差范围内。

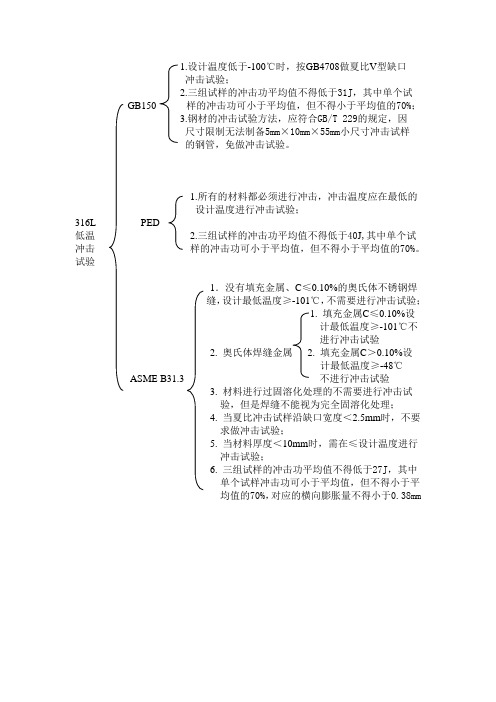
1.设计温度低于-100℃时，按GB4708做夏比V型缺口
冲击试验；
2.三组试样的冲击功平均值不得低于31J，其中单个试
GB150 样的冲击功可小于平均值，但不得小于平均值的70%；
3.钢材的冲击试验方法，应符合GB/T 229的规定，因
尺寸限制无法制备5mm×10mm×55mm小尺寸冲击试样
的钢管，免做冲击试验。

1.所有的材料都必须进行冲击，冲击温度应在最低的
设计温度进行冲击试验；
316L PED
低温 2.三组试样的冲击功平均值不得低于40J,其中单个试冲击样的冲击功可小于平均值，但不得小于平均值的70%。

试验
1．没有填充金属、C≤0.10%的奥氏体不锈钢焊
缝，设计最低温度≥-101℃，不需要进行冲击试验；
1. 填充金属C≤0.10%设
计最低温度≥-101℃不
进行冲击试验
2. 奥氏体焊缝金属 2. 填充金属C＞0.10%设
计最低温度≥-48℃ASME B31.3 不进行冲击试验
3. 材料进行过固溶化处理的不需要进行冲击试
验，但是焊缝不能视为完全固溶化处理；
4. 当夏比冲击试样沿缺口宽度＜2.5mm时，不要
求做冲击试验；
5. 当材料厚度＜10mm时，需在≤设计温度进行
冲击试验；
6. 三组试样的冲击功平均值不得低于27J，其中
单个试样冲击功可小于平均值，但不得小于平
均值的70%，对应的横向膨胀量不得小于0.38mm。

塑料弯曲试验标准塑料弯曲试验的标准是按照GB/T《塑料弯曲性能的测定》进行的。

具体标准如下：1. 试样要求：长度l为80mm±2mm，宽度b为±，厚度h为±。

对于任一试样，其中部1/3的长度内各处厚度与厚度平均值的偏差应不大于2%，宽度与平均值的偏差不应大于3%。

试样截面应是矩形且无倒角。

在每一试验方向上至少应测试5个试样。

如果要求平均值要有更高的精密度，试样数量可能会超过5个，具体的试样数量可用置信区间进行估算。

试样在跨度中部1/3外断裂的试验结果应予作废，并应重新取样进行试验。

若无相关标准时，应从GB/T2918中选择最合适的环境进行试验。

另有商定的，如高温或低温试验除外。

2. 测量试样中部的宽度b精确到；厚度h精确到；计算一组试样厚度的平均值h。

剔除厚度超过平均厚度允许偏差2%的试样样，并用随机选取的试样来代。

3. 调节跨度为试样厚度的16倍士1倍，跨度测量准确至％以内；调节试验速度为//min。

4. 压头、支座与试样应为线接触，并保证与试样宽度的接触线垂直于试样长度方向。

5. 开动万能试验机进行试验。

6. 在规定挠度等于或小于试样厚度的倍时出现断裂的试样，记录其断裂弯曲负荷值。

在达到挠度时不断裂的试样，记录达到规定挠度时的负荷值。

如果产品标准允许超过规定挠度，则要继续进行试验，直到试样破坏或达到最大负荷，记录此时的负荷值。

在达到规定挠度之前断裂且能指示最大负荷的试样，记录其最大负荷。

7. 凡试样破坏位置在试样跨度三等分的中间部分以外时，其结果作废，必须重新取样重新试验。

8. 结果表示小试样弯曲应力或弯曲强度及标准偏差计算与大试样测定时一样。

塑料弯曲试验的目的是确定材料在受到弯曲力作用时的性能表现，这对于评估材料的结构强度和韧性具有重要意义。

xxxxxxxxxxxxxxxxx产品检验实验标准文件编号：版本号：发行日期：编制：审核：审批：一、范围本标准适用于xxxxxxxxxxxxxxxx电动汽车动力蓄电池循环寿命、安全及电性能要求及其试验方法二、规范性引用文件1.GB/T31484-2015《电动汽车用动力蓄电池循环寿命要求及试验方法》2.GB/T31485-2015《电动汽车用动力蓄电池安全要求及试验方法》3.GB/T31486-2015《电动汽车用动力蓄电池电性能要求及试验方法》三、内容本标准共分为三篇：电动汽车用动力蓄电池循环寿命标准；电动汽车用动力蓄电池安全标准；电动汽车用动力蓄电池电性能标准第一篇：电动汽车用动力蓄电池循环寿命标准1 范围本标准规定了电动汽车用动力蓄电池的标准循环寿命的要求、试验方法、检验规则和工况循环寿命的试验方法和检验规则。

本标准适用于装在在电动汽车上的动力蓄电池（以下简称蓄电池）2 规范性引用文件下列文件对于本文件的应用时必不可少的。

凡是注日期的应用文件，仅注日期的版本适用于本文件。

凡是不注日期的引用文件，其最新版本（包括所有的修改单）适用于本文件。

GB/T31484-2015《电动汽车用动力蓄电池循环寿命要求及试验方法》3 术语和定义GB/T231484-2015中界定的以及下列术语和定义适用于本文件3.1单体蓄电池直接将化学能转化为电能的基本单元装置，包括电极、隔膜、电解质、外壳和端子，并被设计成可充电3.2蓄电池模块将一个以上单体蓄电池按照串联、并联或串并联方式组合，且只有一对正负极输出端子，并作为电源使用的组合体。

3.3蓄电池包通常包括蓄电池模块、蓄电池管理模块（不包含BCU）、蓄电池箱以及相应附件，具有从外部获得电能并可对外输出电能的单元3.4蓄电池系统一个或一个以上蓄电池包及相应附件（管理系统、高压电路、低压电路、热管理设备以及机械总成等）构成的能量储存装置3.5额定容量室温下完全充电的蓄电池以1I1（A）电流放电，达到终止电压时所放出的容量（Ah）3.6额定能量室温下完全充电的蓄电池以1I1（A）电流放电，达到终止电压时所放出的能量（Wh）3.7初始容量新出厂的动力蓄电池，在室温下，完全充电后，以1I1（A）电流放电至公司规定的放电终止条件时所放出的容量（Ah）。

砌体抗压强度等级的平均值,标准值和设计值的关系砌体抗压强度等级是指砌体在受压作用下的抗力能力，通常用标准值来表示。

标准值是指在一定条件下，所测得的一组样品的平均数值，可以作为设计值的基础。

设计值是根据标准值和一定的安全系数得出的，用于工程设计中的计算。

在建筑工程中，砌体常常用于墙体的建造，因此其抗压强度等级对建筑结构的稳定性和安全性具有重要意义。

砌体抗压强度等级通常根据《砌体结构抗压强度标准》(GB 13519)进行分类和确定，常见的等级有3.5、7.5、10、15、20、25等。

平均值是指一组数据的算术平均数，可以用来表示一组样品的整体水平。

对于砌体抗压强度等级而言，其平均值可以反映一批样品的整体性能水平。

通常情况下，平均值是通过多次试验得出的，具有一定的代表性和参考价值。

在砌体抗压强度等级的标准值、平均值和设计值的关系中，标准值是通过大量的试验数据得出的，具有较高的稳定性和可靠性，可以作为设计值的参考。

平均值则可以反映一组样品的整体水平，可以在一定程度上代表标准值。

设计值则是根据标准值和一定的安全系数得出的，是在保证结构安全的前提下，具体应用到工程设计和计算中的数值。

当设计工程中需要使用砌体时，首先需要确定砌体的抗压强度等级，然后根据该等级的标准值和一定的安全系数，得出设计值。

设计值需要考虑结构的安全性和稳定性，因此通常会取标准值与安全系数相乘的结果作为设计值。

在实际工程中，砌体抗压强度等级的平均值、标准值和设计值需要进行合理的应用和选择。

一方面，标准值作为一个基准值，可以反映出砌体的实际性能。

平均值则可以作为参考，帮助工程师更全面地了解材料性能。

设计值则需要进行合理的选取，兼顾材料的安全性和经济性。

总之，砌体抗压强度等级的平均值、标准值和设计值之间存在着一定的关系。

这三者在工程设计和实际施工中都具有重要的意义，需要经过科学合理的计算和选择。

只有在充分了解和考虑这些数值之间的关系，才能保证工程结构的安全性和稳定性。

化妆品防腐性能挑战性试验及评价标准化妆品防腐挑战性试验及评价标准投产前对产品防腐体系的可靠性做效能测试是十分必要的，目前，国内外配方设计时普遍采用防腐挑战性试验评价防腐剂的有效性。

防腐挑战性试验更接近实际应用，该方法能够模拟化妆品生产和使用过程中受到高强度的微生物污染的潜在可能性和自然界中微生物生长的最适宜条件，从而避免由微生物污染造成的损失和为消费者健康提供可靠的保证。

1.CTFA推荐的一次加菌防腐挑战性试验及评价标准CTFA的方法初始的霉菌和细菌的接种量分别为10000cfu/g(ml)和1000000cfu/g(ml)(CFU为菌落单位)，要求在第7天时霉菌降低90%，细菌降低99.9%，并且在28天内菌数持续下降。

美国在CTFA评价方法的基础上提出更为严格的标准，即，若单菌接种的三个平行试验中任何一种微生物数量的平均值，在第七天时下降到100 cfu/g(ml)以下，28天全部为0，则视为效果优良通过挑战试验;若第七天时下降到1000 cfu/g(ml)以下，则视为勉强通过;若单菌接种的任何一种微生物，任何一个平行样达不到上述标准，也达不到CTFA的要求，防腐体系则评定为无效。

2.国内参照CTFA加菌防腐挑战性试验及评价标准初始接种细菌量1000000 cfu/g(mL)(1)第28天时，样品中含细菌或霉菌,1000cfu/g(mL)该样品不能通过微生物攻击的挑战试验，表明样品的防腐体系不能有效地志到抑制微生物的作用，产品在生产、贮藏和使用中很容易受到微生物的污染。

(2)第28天时，样品中含细菌或霉菌在100 cfu/g-1000 cfu/g(mL)，该样品有条件地通过挑战试验，即当产品中蛋白质或其他动植物材料成分不是特别高，同时生产的卫生环境符合要求，包装物不易发生二次污染时，该防霉体系可以使用，否则不能。

(3)第28天时，样品中含细菌或霉菌在10 cfu/g-100 cfu/g(mL)，表明该样品的防腐体系对微生物有较强的抑杀效果，通过挑战试验，产品在生产、贮藏和使用时不容易受到微生物污染。

混凝土强度的平均值,标准值和设计值之间的关系混凝土强度是指混凝土在受压、弯曲、剪切等力作用下所能承受的最大荷载。

混凝土强度的平均值、标准值和设计值是工程建设中常用的指标，它们之间有着密切的关系。

平均值是指在试验中得到的多次单个样本混凝土强度值的平均值。

平均值是一个统计值，可以根据大量的样本数据计算出来，具有一定代表性。

平均值可以反映混凝土整体的强度水平。

标准值是指混凝土强度的极限状态下的数值，也就是规定的强度等级下的最小值。

标准值是一个基准值，具有可比性和可预测性。

标准值的确定依据国家标准相关规定。

设计值是根据工程设计要求而确定的混凝土强度值。

设计值是根据实际情况而设定，可以用来指导工程建设和施工。

设计值一般要考虑到工程实际情况，比如地质条件、结构形式、荷载等因素，设计值一般比标准值要大。

平均值、标准值和设计值之间的关系是：平均值是实验结果的统计值，反映出混凝土的整体强度水平；标准值是规定的一个值，反映出归一化的强度水平；而设计值则是实际需要的值，是根据实际情况计算得到的。

三者之间的关系可以表述为：设计值≥标准值≥平均值也就是说，设计值一般大于标准值，而标准值又大于平均值。

设计值要满足工程的实际需要，而标准值则是规范化的数值，平均值则是基于试验结果得到的统计值。

由于混凝土的强度会受到诸多因素的影响，所以平均值和标准值并不是完全可靠的，有时设计值需要进行一些修正。

总之，混凝土的强度是一个非常重要的参数，在工程建设中需要做出合理的设计和选材，确保其安全可靠。

平均值、标准值和设计值之间的关系可以帮助我们更好地理解混凝土强度的特点和规律，为实际工程建设提供科学的指导。

试验结果的误差及评定方法（新标准)一、水泥细度:以两次试验的平均值为结果，精确至0。

1％若两次筛余结果绝对误差大于0.5%时，（筛余值大于5。

0%时，可放至1。

0%)，应再做一次试验，取两次相近结果的算术平均值作为最终结果.安定性（雷氏夹法）以两个试件煮后增加距离的平均值不大于5.0mm时，为合格当两个试件的值相差超过4。

0mm时，应重作试验。

再如此，则认为该水泥安定性不合格。

抗折强度取三个试件的平均值，精确至0。

1Mpa当三个强度值中有超过平均值±10%的,应剔除后再平均，以平均值作为试验结果。

抗压强度加荷速度:2400n/s±200n/s以六个试件的算术平均值，精确至0.1Mpa如六个强度值中有一个值超过平均值±10%的，应剔除后，以剩下的5个算术平均值为最后结果。

如5个值中再有超过平均值±10％的，则此组试件无效。

二、粗集料筛分试样:称量精确至0.1%各筛分计筛余量及筛底存量的总和与筛前试样总质量相比，相差不得超过总质量的0.5％分计、累计筛余精确至0。

1%由筛底存量除以扣除损耗后的干燥集料总质量计算0.075mm筛的通过率。

试验结果以两次试验的平均值表示。

精确至0。

1％当两次试验结果P0。

075的差值超过1%，试验应重新进行。

表观密度试验结果精确至小数点后3位含水率精确至0。

1%以两次试验结果的平均值为最后结果吸水率精确至0.01%以两次试验结果的平均值为最后结果.堆积密度精确至小数点后2位以两次试验结果的平均值为测定值含泥量精确至0.1%以两次试验的平均值作为测定值两次结果的差值超过0。

2%，应重新取样试验针片状含量精确至于0.1%压碎值试样精确至1g结果精确至0。

1%以三次平均值为测定结果。

三、细集料筛分称烘干试样500g，准确至0。

5g称量各筛筛余试样的质量,精确至0.5g，所有各筛的分计筛余量和底盘中剩余的总量与筛分前的试样总量，相差不得超过后者的1％分计筛余、累计筛余结果准确至0.1%应进行两次平行试验，以试验结果的算术平均值作为测定值，如两次试验所行的细度模数之差大于0。