高等数学(高等教育出版社)第十章D10_4重积分的应用ok
- 格式:ppt
- 大小:992.50 KB
- 文档页数:23

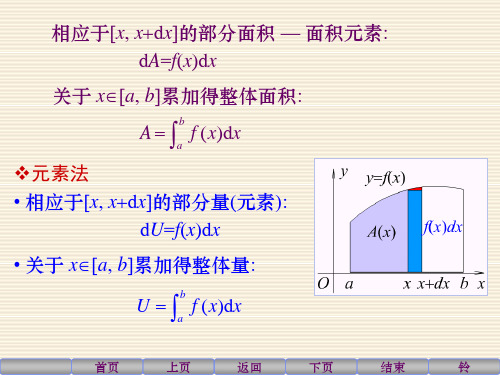




第10章 重积分内容总结一、计算二重积分的方法:(,)DI f x y d σ=⎰⎰1、利用直角坐标计算二重积分 d d x d y σ= (1)若12{(,)()(),}=≤≤≤≤D x y x y x a x b ϕϕ,则21()()(,)(,)=⎰⎰⎰⎰bx ax Df x y d dx f x y dy ϕϕσ(2)12{(,)()(),}=≤≤≤≤D x y y x y c y d ψψ,则21()()(,)(,)=⎰⎰⎰⎰dy cy Df x y d dy f x y dx ψψσ2、利用极坐标计算二重积分cos ,sin ,x y d d d ρθρθσρρθ=== (c o s ,s i n )DI f d d ρθρθρρθ=⎰⎰ (1)若12{(,)|,()()}=≤≤≤≤D ρθαθβϕθρϕθ,则21()()(cos ,sin )I d f d βϕθαϕθθρθρθρρ=⎰⎰(2)若{(,)|,0()}=≤≤≤≤D ρθαθβρϕθ,则()(cos ,sin )I d f d βϕθαθρθρθρρ=⎰⎰(3)若{(,)|02,0()}=≤≤≤≤D ρθθπρϕθ,则2()00(cos ,sin )I d f d πϕθθρθρθρρ=⎰⎰(4)若2222{(,)(),0}{(,)0,02cos }D x y x a y a y a πρθθρθ=-+≤≥=≤≤≤≤,则22cos 0(cos ,sin )a I d f d πθθρθρθρρ=⎰⎰(5)若2222{(,)(),0}{(,)0,02sin }Dx y y a x a x a πρθθρθ=-+≤≥=≤≤≤≤,则2sin 0(cos ,sin )a I d f d πθθρθρθρρ=⎰⎰二、计算三重积分的方法(,,)I f x y z dv Ω=⎰⎰⎰1、 利用直角坐标计算三重积分 d v d x d y d z= (1)投影法(先一后二) 若12{(,,)(,),(,)(,)}xy x y z x y D z x y z z x y Ω=∈≤≤ 其中12{(,),()()}xy xy D prj x y a x b y x y y x =Ω=≤≤≤≤ 则2211()(,)()(,)(,,)by x z x y ay x z x y I dx dy f x y z dz =⎰⎰⎰(2)截面法(先二后一)若12{(,,)(,),}z x y z x y D c z c Ω=∈≤≤则21(,,)zc c D I dz f x y z dxdy =⎰⎰⎰2、利用柱面坐标计算三重积分c o s ,s i n ,x y z z ρθρθ===,dvd d dz ρρθ= (cos ,sin ,)I f z d d dz ρθρθρρθΩ=⎰⎰⎰几种特殊情况(1)若222{(,,)0,}{(,,)02,0,0}x y z z H x y R z R z H ρθθπρΩ=≤≤+≤=≤≤≤≤≤≤则20(cos ,sin ,)R HI d d f z dz πθρρρθρθ=⎰⎰⎰(2)若{(,,}{(,,)02,0,}x y z z H z H z H ρθθπρρΩ=≤=≤≤≤≤≤≤则20(cos ,sin ,)HHI d d f z dz πρθρρρθρθ=⎰⎰⎰(3)若Ω是由上半球面z =与上半锥面z =围成的闭区域即{(,,)02,0,z a z ρθθπρρΩ=≤≤≤≤≤≤则20(cos ,sin ,)aId d f z dz πρθρρρθρθ=⎰⎰(4)若Ω是由上半球面z =与旋转抛物面22x y z a+=围成的闭区域即2{(,,)02,0,z a z aρρθθπρΩ=≤≤≤≤≤≤则220(cos ,sin ,)aaId d f z dz ρπθρρρθρθ=⎰⎰⎰3、利用球面坐标计算三重积分2s i n c o s ,s i n s i n ,c o s ,s i n x r y r z r d v r d r d dϕθϕθϕϕϕθ==== 2(sin cos ,sin sin ,cos )sin I f r r r r drd d ϕθϕθϕϕϕθΩ=⎰⎰⎰几种特殊情况(1)若Ω是球域2222{(,,)}{(,,)02,0,0}x y z x y z R r r R θϕθπϕπΩ=++≤=≤≤≤≤≤≤220sin (sin cos ,sin sin ,cos )RI d d f r r r r dr ππθϕϕϕθϕθϕ=⎰⎰⎰(2)若Ω是球域22222{(,,)()}{(,,)02,0,02cos }x y z x y z R R r r R πθϕθπϕϕΩ=++-≤=≤≤≤≤≤≤ 222cos 2000sin (sin cos ,sin sin ,cos )R I d d f r r r r dr ππϕθϕϕϕθϕθϕ=⎰⎰⎰(3)若Ω是由不等式2222()x y z R R ++-≤与222x y z +≤围成的闭区域4{(,,)02,0,02cos }}Ω=≤≤≤≤≤≤r r R πθϕθπϕϕ 22cos 2000sin (sin cos ,sin sin ,cos )R I d d f r r r r dr ππϕθϕϕϕθϕθϕ=⎰⎰⎰。
MATH YTU1第四节一、立体体积二、曲面的面积三、物体的质心四、物体的转动惯量五、物体的引力重积分的应用MATH YTU21. 曲顶柱体的顶为曲面),,(y x f z =则其体积为∫∫=Dyx y x f V d d ),(,),(D y x ∈2. 空间有界域Ω的体积为∫∫∫Ω=zy x V d d d 一、立体体积例1MATH YTU3例1. 求由解:计算第一卦限部分体积22224x y z a ++=与柱面所围立体的体积(含在柱面内的).222x y ax +=21:0,0,2.D x y y ax x ≥≥≤−投影区域为顶面为球面2224()z a x y =−+oxyza2MATH YTU4122214D V a x y dxdy =−−∫∫31164(34).9V V a π==− 注意:被积函数和区域的对称性.第一卦限部分体积22202cos 4a d a r rdrπθθ=−∫∫21:0,0,2.D x y y ax x ≥≥≤−Doy x23308(1sin )d 3a πθθ=−∫382()323a π=−面积MATH YTU5γMAd zσd nx yz So 设光滑曲面D y x y x f z S ∈=),(,),(:则面积A 可看成曲面上各点),,(z y x M 处小切平面的面积d A 无限积累而成.设它在D 上的投影为d σ,Ad cos d ⋅=γσ),(),(11cos 22y x f y x f y x ++=γσd ),(),(1d 22y x f y x f A y x ++=(称为面积元素)则γγMnG σd 二、曲面的面积MATH YTU6故有曲面面积公式σd ),(),(122∫∫++=Dy x y x f y x f A yx y z xz A Dd d )()(122∫∫∂∂+∂∂+=若光滑曲面方程为zy z x y x A d d )()(122∂∂+∂∂+=∫∫,),(,),(z y D z y z y g x ∈=则有zy D 即MATH YTU7xz x y zyA d d )()(122∂∂+∂∂+=∫∫若光滑曲面方程为,),(,),(x z D x z x z h y ∈=若光滑曲面方程为隐式,0),,(=z y x F 则则有yx z yz x D y x F F y zF F x z ∈−=∂∂−=∂∂),(,,∫∫=∴A yx D xz D zzy x F F F F 222++,0≠z F 且yx d d 例2MATH YTU8y x z =被柱面222R y x =+解: 曲面在xoy 面上投影为,:222R y x D ≤+则y x z z A D y x d d 122∫∫++=yx y x Dd d 122∫∫++=rr r Rd 1d 0220∫∫+=πθ])1)1([32232−+=R π所截出的面积A .例2. 计算双曲抛物面质心MATH YTU9设平面有n 个质点,(,),k k x y 其质量分别,),,2,1(n k m k "=该质点系关于y 轴和x 轴1ny k kk M x m ==∑1nx k kk M y m ==∑分别位于为三、物体的质心的静力矩分别为:MATH YTU10(,),x y 该质点系的质心坐标设为11,n nk y k k k k x m M x m ==⋅==∑∑根据质心定义,可导出质心公式11,nnk x k k k k y m M y m ==⋅==∑∑11,nk ky k nkk x mM x Mm====∑∑11,nk kx k nkk y mM y Mm====∑∑MATH YTU11若物体为占有xOy 面上区域D 的平面薄片,其,),(y x μ为面密度该物体位于(x , y ) 处的微元d σxDyod σ(,)x y 关于y 轴和x 轴的静力矩分别为:d (,)y M x x y d μσ=⋅d (,)x M y x y d μσ=⋅MATH YTU12则平面薄片D 关于y 轴和x 轴的静力矩分别为:(,)d d Dy M x x y x yμ=∫∫(,)d d DM x y x yμ=∫∫则它的质心坐标为d (,)y M x x y d μσ=⋅d (,)x M y x y d μσ=⋅(,)d d Dx M y x y x yμ=∫∫注意平面薄片D 的质量为,y M x M=x M y M=MATH YTU13yx y x y x y x x x D D ∫∫∫∫=d d ),(d d ),(μμy x y x y x y x y y D D ∫∫∫∫=d d ),(d d ),(μμ,c μ=,d d Ayx x x D ∫∫=Ayx y y D ∫∫=d d (A 为D 的面积)得D 的形心坐标:则质心坐标为MM y =MM x =x M y M —对x 轴的静矩—对y 轴的静矩MATH YTU14设物体占有空间区域Ω, 有连续分布的密度函数.),,(z y x ρ该物体位于(x , y , z ) 处的微元(,,)d x x y z vρ⋅d yz M =xΩyo zd v关于yOz 平面的静矩为:d v注意Ω的质量为(,,)d (,,)d d d M x y z v x y z x y zρρΩΩ==∫∫∫∫∫∫MATH YTU15(,,)d d d (,,)d d d x x y z x y zx y z x y zρρΩΩ=∫∫∫∫∫∫(,,),x y z 质心坐标设为根据质心定义,yz M x M=同理可得,(,,)d d d (,,)d d d zx y x y z x y z M y Mx y z x y zρρΩΩ==∫∫∫∫∫∫MATH YTU16(,,)d d d (,,)d d d xy z x y z x y z M z Mx y z x y zρρΩΩ==∫∫∫∫∫∫,),,(常数时当≡z y x ρ则得形心坐标:,d d d Vz y x x x ∫∫∫Ω=,d d d Vzy x y y ∫∫∫Ω=Vz y x z z ∫∫∫Ω=d d d ()的体积为Ω=∫∫∫Ωz y x V d d d 通式MATH YTU17()V ρ其中V 是可以是平面薄片或空间立体,相应的积分(,,),x y z 质心坐标设为或(,),x y 则()d ,()d V Vx V vV vρρ∫∫x =()d ,()d VVy V vV vρρ∫∫y =()d ()d V Vz V vV vρρ∫∫z =对应二重积分或三重积分;d v 相应的分别为平面面积元素或空间体积元素;相应的即是面密度或是体密度。