有限元在土木工程中的应用

有限元方法在基础沉降计算中的应用及工程
实例
有限元方法在基础沉降计算中的应用及工程实例
有限元方法是一种分析复杂结构问题的数值解法，它可以用于计算建筑物和地基之间的水力平衡。

本文旨在介绍有限元方法在基础沉降计算中的应用及相关的工程实例。

首先，在基础沉降计算中，有限元方法是一种重要的数值解法，特别适用于复杂的地质结构和土体性质的情况，可以对土层的支撑效果进行准确的计算。

根据有限元原理，所有土体可以被划分成更小的有限单元，并以此来代表计算中的空间位置。

该方法可以更加准确地计算土体的各个部分的应力及变形，从而估算出沉降量。

其次，有限元方法在基础沉降分析中的应用不仅能确定沉降量，而且还能准确分析地基在荷载作用下的变形状态，从而有利于维修和改善软土地基。

以上海市某基础桩基础改造工程为例，该工程使用了有限元方法来对陆地开埭及周边环境进行分析，结果显示沉降量最大可达到20mm以上，一般沉降量在6~10mm之间，但这并不影响基础改造工程的正常施工。

此外，目前有限元方法已经得到了广泛的应用，其中包括深埋桩基础沉降分析、岸壁沉降分析、多层结构分析、斜坡稳定分析等。

比如重庆市一个桥梁工程，工程师使用有限元方法对桥墩进行了沉降分析，根据有限元分析结果，可知桥墩沉降量可在2.4mm左右，比根据现场试验结果得到的沉降量更接近实际情况。

最后，有限元方法在基础沉降计算中有着广泛的应用，能够更准确地计算沉降量和土体的变形状态，并且可以更好地评估地基的稳定性。

然而，有限元方法仍有些限制，比如无法准确模拟岩石地基的变形及沉降量，也不能解决桩眼内土体的塑性变形及施工沉降量等问题，因此，有限元分析仍然需要与现场实验结合起来，以确保分析结果的准确性。

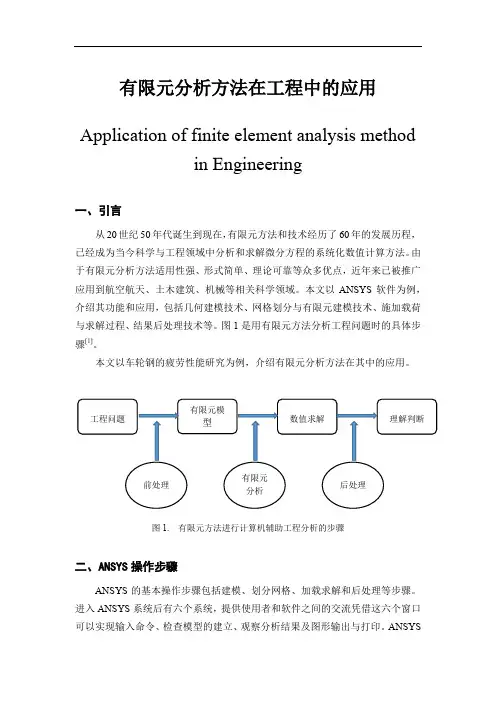
有限元分析方法在工程中的应用Application of finite element analysis methodin Engineering一、引言从20世纪50年代诞生到现在，有限元方法和技术经历了60年的发展历程，已经成为当今科学与工程领域中分析和求解微分方程的系统化数值计算方法。

由于有限元分析方法适用性强、形式简单、理论可靠等众多优点，近年来已被推广应用到航空航天、土木建筑、机械等相关科学领域。

本文以ANSYS软件为例，介绍其功能和应用，包括几何建模技术、网格划分与有限元建模技术、施加载荷与求解过程、结果后处理技术等。

图1是用有限元方法分析工程问题时的具体步骤[1]。

本文以车轮钢的疲劳性能研究为例，介绍有限元分析方法在其中的应用。

图1. 有限元方法进行计算机辅助工程分析的步骤二、ANSYS操作步骤ANSYS的基本操作步骤包括建模、划分网格、加载求解和后处理等步骤。

进入ANSYS系统后有六个系统，提供使用者和软件之间的交流凭借这六个窗口可以实现输入命令、检查模型的建立、观察分析结果及图形输出与打印。

ANSYS各窗口及工具条如图2所示。

图2. ANSYS的窗口及工具条1、建立模型首先必须指定作业名和分析标题，接着使用PREP7前处理器定义单元类型、单元实常数、材料特性，然后建立几何模型。

需要注意的是，ANSYS的GUI界面下没有类似WORD中的后退操作按钮，所以就出现了一个常见问题：做错一步操作如何后退？这里可以采用三种方法：（1）建模阶段可以使用Delete(删除)图元命令，划分网格阶段可以使用Clear（清除）单元命令。

（2）每完成一个模块的操作，都用SA VE AS保存数据到不同名的数据库文件中，出错后点击Resum Form恢复。

（3）使用命令：UNDO，ON以便激活ANSYS内部的返回命令。

本文以车轮钢为例，建立好的模型与图2类似，只是未划分网格。

2、单元网格划分一个实体模型进行网格划分（meshing）之前必须指定所产生的单元属性（element attribute）。

论文题目：钢筋混凝土有限元分析技术在结构工程中的应用学生姓名：刘畅学号：2014105110学院：建筑与工程学院2015 年06月30日有限元分析在钢筋混凝土结构中的应用【摘要】在国内外的土木工程中，钢筋混凝土结构因具有普遍性、可靠性良好、操作简单等优点，而得到了广泛的应用。

钢筋混凝土结构是钢筋与混凝土两种性质截然不同的材料组合而成，由于其组合材料的性质较为复杂，同时存在非线性与几何线形的特征，应用传统的解析方法进行材料的分析与描述在受力复杂、外形复杂等情况下较为困难，往往不能得到准确的数据，给工程安全带来隐患。

而有限元分析方法则充分利用现代电子计算机技术，借助有限元模型有效解决了各种实际问题。

【关键词】有限元分析；钢筋混凝土结构；应用随着计算机在工程设计领域中的广泛应用，以及非线性有限元理论研究的不断深入，有限元作为一个具有较强能力的专业数据分析工具，在钢筋混凝土结构中得到了广泛的应用。

在现代建筑钢筋混凝土结构的分析中，有限元分析方法展现了较强的可行性、实用性与精确性。

例如：在计算机上应用有限元分析法，对形状复杂、柱网复杂的基础筏板，转换厚板，体型复杂高层建筑侧向构件、楼盖，钢- 混凝土组合构件等进行应力，应变分析，使设计人员更准确的掌握构件各部分内力与变形，进而进行设计，有效解决传统分析方法的不足，满足当前建筑体型日益复杂，工程材料多样化的实际情况。

但是在有限元分析方法的应用中，必须结合钢筋混凝土结构工程的实际情况，选取作为合理的有限元模型，才能保证模拟与分析结果的真实性、精确性与可靠性。

在钢筋混凝土结构工程中，非线性有限元分析的基本理论可以概括为：1）通过分离钢筋混凝土结构中的钢筋、混凝土，使其成为有限单位、二维三角形单元，钢箍离散为一维杆单元，以利于分析模型的构建；2）为了合理模拟钢筋、混凝土之间的粘结滑移关系，以及裂缝两侧混凝土的骨料咬合作用，可以根据实际需要在钢筋、混凝土之间，以及裂缝两侧的混凝土之间设置相应的连结单元；3）结合钢筋混凝土结构的材料性质，选用与各类单元相适应的本构关系，即应力应变关系，此类关系为线性或非线性均可；4）与一般的有限元分析方法相同，非线性有限元分析也需要确定各单元的刚度矩阵，并且将其组合为钢筋混凝土结构的整体刚度矩阵，根据结构所受到的各种荷载作用与约束，计算出有限元结点的位移情况、单元应变与单元应力等。

如何在工程力学中应用有限元方法？在现代工程领域中，工程力学的重要性不言而喻。

而有限元方法作为一种强大的数值分析工具，为解决复杂的工程力学问题提供了高效、准确的途径。

那么，究竟如何在工程力学中应用有限元方法呢？要理解有限元方法在工程力学中的应用，首先得明白什么是有限元方法。

简单来说，有限元方法是将一个连续的求解域离散为一组有限个、且按一定方式相互联结在一起的单元组合体。

通过对每个单元的分析，最终得到整个求解域的近似解。

在工程力学中，有限元方法有着广泛的应用场景。

比如，结构力学分析就是其中一个重要的方面。

当我们设计一座桥梁、一栋高楼或者一架飞机的框架结构时，需要知道这些结构在各种载荷作用下的应力、应变和位移情况。

传统的理论计算方法在处理复杂结构时往往力不从心，而有限元方法则能够很好地应对。

我们以桥梁结构为例。

首先，需要对桥梁的几何形状和材料特性进行准确的描述。

然后，将桥梁结构离散化为众多的小单元，比如三角形单元或者四边形单元。

接下来，为每个单元建立力学方程，考虑其受到的外力、内力以及边界条件等因素。

通过求解这些单元的方程，再将结果组合起来，就可以得到整个桥梁结构的力学响应。

这样，工程师就能够清楚地了解桥梁在不同载荷下哪些部位可能会出现过大的应力，从而进行优化设计，确保桥梁的安全性和可靠性。

再比如，在流体力学领域，有限元方法也发挥着重要作用。

对于复杂的流体流动问题，如飞机机翼周围的气流、汽车发动机内部的燃油流动等，有限元方法可以帮助我们模拟流体的速度、压力和温度分布等特性。

通过建立合适的流体控制方程，并将求解区域离散化为单元，就能够对流体的流动行为进行准确的预测和分析。

除了结构力学和流体力学，有限元方法在热传递问题中同样表现出色。

在电子设备的散热设计、发动机的冷却系统设计等方面，需要了解热量在物体内部的传递和分布情况。

有限元方法可以将物体离散为单元，考虑热传导、对流和辐射等传热方式，从而计算出物体内部的温度场。

基于有限元分析的土木工程结构设计优化土木工程是研究土木结构设计、建造和维护的学科，其中结构设计是土木工程的重要组成部分。

在土木工程的设计过程中，利用有限元分析作为一种计算工具，可以对结构进行数字模拟和分析，为结构设计提供可靠的支持，最终实现结构设计的优化。

1. 有限元分析在土木工程中的作用有限元分析是一种数值计算方法，它将复杂的结构分割为有限数量的小单元，并对每个小单元进行边界条件和材料特性的设定，然后通过数学和物理的算法来模拟和计算结构的行为。

有限元分析可以预测结构在不同载荷和边界条件下的应力、应变、变形等响应，从而为结构设计提供重要的指导。

2. 有限元分析在土木工程结构设计中的应用有限元分析在土木工程结构设计中具有广泛的应用，例如在建筑物、桥梁、隧道和水坝等项目中。

通过有限元分析，设计师能够优化结构的设计，从而提高结构的安全性、稳定性和经济性。

2.1 结构强度分析在土木工程结构设计中，有限元分析可以用于评估结构在不同载荷情况下的强度。

例如，在桥梁设计中，通过有限元分析可以确定桥梁各个部件的受力情况，进而确定结构的截面尺寸和材料的选型。

2.2 结构稳定性分析有限元分析还可以用于评估结构的稳定性。

对于长跨度桥梁或高层建筑等结构，稳定性是一个非常重要的考虑因素。

有限元分析可以模拟结构在受到外力作用时的变形和位移，进而判断结构是否存在稳定性问题。

2.3 结构振动分析有限元分析还可以用于评估结构的振动特性。

对于桥梁和高层建筑等结构，振动是一个重要的考虑因素。

通过有限元分析，可以预测结构在自然振动频率下的响应，并进一步进行结构设计优化。

3. 有限元分析的优化应用在土木工程结构设计中，有限元分析不仅可以用于评估结构的性能，还可以进行结构设计的优化。

3.1 结构材料优化有限元分析可以模拟不同材料特性下的结构行为，并通过对比分析，选取最优材料以满足设计要求。

例如，在建筑物设计中，可以通过有限元分析来确定适合的混凝土强度等级，以充分利用材料的承载能力，同时保证结构的安全性。

在土木工程中有限元运用的实例哎，说起土木工程里有限元法的运用啊，那可真是无处不在，用处多多。

你想啊，土木工程师们天天跟高楼大厦、桥梁隧道打交道，这些玩意儿结构复杂，受力情况也五花八门，光靠经验和直觉，那哪行？所以啊，有限元法就成了他们的得力助手。

我就拿我自己身边的事儿来说吧，前两年我参与了一个大型商业综合体的建设项目，那可真是个大工程，好几栋高楼，底下还有好几层的商业裙楼，再加上地下室，结构复杂得跟迷宫似的。

在设计阶段，我们团队就遇到了一个大难题，就是那个商业裙楼和塔楼交接的地方，受力特别复杂，各种剪力、弯矩、扭矩都搅和在一起，让人头疼不已。

这时候，有限元法可就派上用场了。

我们用专业的有限元分析软件，把整个结构模型建立起来，然后输入各种材料参数、荷载条件，接着就让软件去跑计算。

说实话，那软件跑起来可真是费时费力，得等上好几天才能出结果，但你别说，等结果一出来，那受力分布图、变形图、应力图，一目了然，清清楚楚。

你瞧，那交接处的受力情况，通过有限元分析，我们就能清楚地看到哪些地方应力集中，哪些地方变形过大，这样就能有针对性地优化设计方案。

比如说，我们发现某个部位的应力超出了材料的许用应力，那我们就得加强那里的配筋，或者调整结构尺寸，让应力分布得更均匀一些。

这样一来，整个结构的安全性就大大提高了，咱们心里也踏实多了。

再来说说桥梁工程吧。

我有一次去参观了一座刚建成的大桥，那桥可真壮观，横跨在一条大江之上，气势恢宏。

我跟大桥的设计师聊了聊，他告诉我，在设计这座桥的时候，他们也用了有限元法。

你想啊，那桥那么长，那么重，还得承受各种车辆荷载、风荷载，甚至还得考虑地震的影响，这受力情况得多复杂啊！设计师们就用有限元法对整个桥梁结构进行了详细的受力分析。

他们考虑了各种可能的荷载组合，还模拟了桥梁在各种极端条件下的变形和应力分布。

这样一来，他们就能准确地评估出桥梁的承载能力和安全性，确保大桥在各种情况下都能稳稳当当的。

岩土工程专业是解决各类工程中关于岩石、土的工程技术问题的科学。

虽然岩土工程计算机分析在大多数情况下只能给出定性分析结果，但岩土工程计算机分析对工程师决策是非常有意义的。

开展岩土工程问题计算机分析研究是一个重要的研究方向。

岩土工程问题计算机分析范围和领域很广，随着计算机技术的发展，计算分析领域还在不断扩大。

1、复杂系统的力学变位分析，如高边坡、深基坑、隧道、大型地下洞室、堤防、桩基、码头、大坝、桁架等或其它复杂的非规则实体的变位和内力（应力、应变、拉压弯剪扭等）。

2、土木工程开挖、建筑、回填引起的地基或建筑的应力、变位、渗流、固结、沉降等变化过程仿真。

3、复杂系统的碰撞、打击(打桩)、地震、损伤、裂缝、破碎、屈曲、爆破、地震、蠕变、水击、热分析、热固耦合等高度非线性仿真计算、安全评估等。

岩土介质的力学性质非常复杂，影响其应力和变形的因素很多，例如岩土的结构、孔隙、密度、应力历史、荷载特征、孔隙水及时间效应等等，这种复杂性决定了技术人员在计算有关岩土问题时往往需要做一些针对具体问题的创新性研究或改进。

元计算核心技术pFEPG以高度开放性和广泛适应性非常适合于此类问题的计算。

它可以根据用户需求，用极短的时间来解决问题（例如增加一种新的单元类型，或是增加新的材料本构模型等等），可以方便地人为控制或修改有限元计算过程中的任何一个细节或参数。

而使计算不再是一个黑匣子，保证计算分析正确合理，达到预测并且指导设计施工的目的。

岩土工程领域应用案例：1、在岩土开挖过程中的应用在贵州省索风营水电站地下厂房围岩稳定性三维有限元分析中，利用pFEPG的前处理功能完成地下厂房及地层分布的造型，并用组合网格法进行网格剖分。

计算范围、地层河床及厂房区位置图地下厂房结构及局部地形地质展示图洞室群结构三维有限元网格图软弱结构面fj2、fj5、fj4部分网格图通过pFEPG自动生成并编制了三维的渗流场计算程序，对施工期渗流场进行了初步分析，首次提出计算渗流场自由面的死（活）结点法，该方法实践证明计算简单、效率较高。

基于有限元分析的土木工程结构力学性能研究摘要：随着社会和经济的迅猛提升，为土木工程提供良好发展的机遇，工程项目逐渐向现代化发展方向推进，土木工程结构也日渐复杂化，这是人类生产生活的物质需求，更是人类的精神追求。

随着我国超高建筑、巨型桥梁以及防洪大坝等大型、复杂的工程数量不断增多，为土木工程结构提出更高的要求，需要加大可靠性的深入研究。

有限元分析技术的出现为解决上述问题提供了一种可靠的方法。

近年来，随着计算技术的发展、分析精度和可靠性的提高，以及良好的可视化性能，有限元分析方法在土木工程领域得到了广泛采用。

目前，常用的有限元分析软件主要有ABAQUS、ANSYS、MIDAS 等。

关键词：有限元；土木工程；结构力学；引言土木工程是为人类生产生活提供服务的各种工程设施，随着社会的不断进步和经济的飞速发展，土木工程项目越来越现代化、复杂化，超高层建筑、巨型桥梁、防洪大坝等工程层出不穷，在满足人们物质和精神需求的同时，也对工程结构可靠性提出了更高要求。

1土木工程结构可靠性研究具有重要的意义1.1土木工程结构可靠性的含义分析土木工程结构可靠性是指在规定的实践和条件下，工程结构所具备的安全性、实用性和耐久性。

我国地质与气候情况差异较大，为工程结构设计带来较高的要求，安全性是能够承受在施工和使用期间可能出现的各种作用，并在偶然事件发生时以及发生后结构整体的稳定性；适用性是在正常使用期间内能够发挥良好的工作性能；耐久性为工程结构具有足够的耐久性能，结构在规定时间下完成这三者能力被称为结构的可靠性。

1.2土木工程结构可靠性研究具有现实需求及未来发展的重要意义近年来我国土木工程事故发生较多，例如大型桥梁的折断、建筑房屋的骤然倒塌，为人民的生命财产安全带来重大影响，加大对土木工程结构可靠性的研究，促进土木结构设计水平的不断提升，优化工程企业内部管理，夯实工程施工管理，为实现工程建设提供可靠的保障。

土木工程结构的可靠性是关系着广大人民生命财产安全的关键，是依法建设工程的重要基础，促进工程质量的有力提升，土木工程整体未来可持续发展具有重要意义。