【物理】物理临界状态的假设解决物理试题的专项培优练习题及答案

备战高考物理 临界状态的假设解决物理试题 培优练习(含答案)附答案解析一、临界状态的假设解决物理试题1．一带电量为＋q 、质量为m 的小球从倾角为θ的光滑的斜面上由静止开始下滑．斜面处于磁感应强度为B 的匀强磁场中，磁场方向如图所示，求小球在斜面上滑行的速度范围和滑行的最大距离．【答案】m gcosθ/Bq ， m 2gcos 2θ/(2B 2q 2sinθ) 【解析】 【分析】 【详解】带正电小球从光滑斜面下滑过程中受到重力m g 、斜面的支持力N 和洛伦兹力f 的作用于小球下滑速度越来越大，所受的洛伦兹力越来越大，斜面的支持力越来越小，当支持力为零时，小球运动达到临界状态，此时小球的速度最大，在斜面上滑行的距离最大 故cos mg qvB θ= 解得：cos mg v qBθ=，为小球在斜面上运动的最大速度 此时小球移动距离为：22222cos 2(2sin )v m g s a B q θθ==．2．质量为m 2=2Kg 的长木板A 放在水平面上，与水平面之间的动摩擦系数为0.4；物块B （可看作质点）的质量为m 1=1Kg ，放在木板A 的左端，物块B 与木板A 之间的摩擦系数为0.2.现用一水平向右的拉力F 作用在木板A 的右端，让木板A 和物块B 一起向右做匀加速运动．当木板A 和物块B 的速度达到2 m/s 时，撤去拉力，物块B 恰好滑到木板A 的右端而停止滑动，最大静摩擦力等于动摩擦力，g=10m/s 2，求：（1）要使木板A 和物块B 不发生相对滑动，求拉力F 的最大值； （2）撤去拉力后木板A 的滑动时间； （3）木板A 的长度。

【答案】（1）18N （2）0.4s （3）0.6m 【解析】 【详解】（1）当木板A 和物块B 刚要发生相对滑动时，拉力达到最大以B 为研究对象，由牛顿第二定律得1111m g m a μ=可得2112m/s a g μ==．再以整体为研究对象，由牛顿第二定律得212121 ))F m m g m m a μ-+=+（（ 故得最大拉力18F N =；（2）撤去F 后A 、B 均做匀减速运动，B 的加速度大小仍为1a ，A 的加速度大小为2a ，则 2121122)m m g m g m a μμ+-=（解得225m/s a =故A 滑动的时间220.45v t s s a === （3）撤去F 后A 滑动的距离22122m=0.4m 225v x a ==⨯B 滑动的距离22212m=1m 222v x a ==⨯故木板A 的长度210.6m L x x =-=．【点睛】解题的关键是正确对滑块和木板进行受力分析，清楚滑块和木板的运动情况，根据牛顿第二定律及运动学基本公式求解。

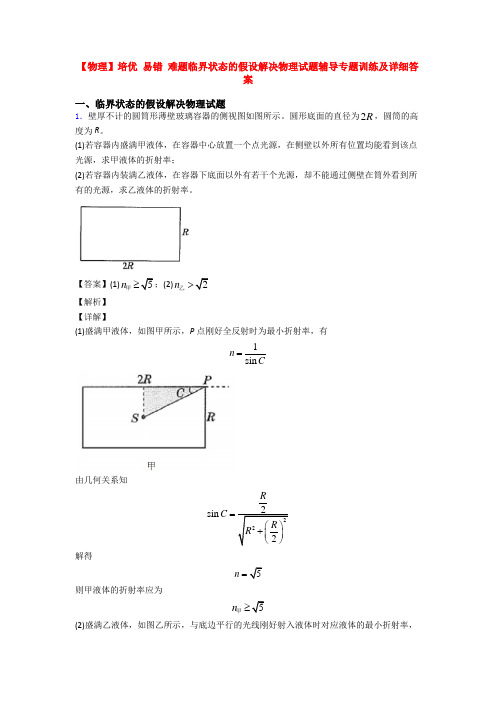
【物理】培优 易错 难题临界状态的假设解决物理试题辅导专题训练及详细答案一、临界状态的假设解决物理试题1．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

圆形底面的直径为2R ，圆筒的高度为R 。

(1)若容器内盛满甲液体，在容器中心放置一个点光源，在侧壁以外所有位置均能看到该点光源，求甲液体的折射率；(2)若容器内装满乙液体，在容器下底面以外有若干个光源，却不能通过侧壁在筒外看到所有的光源，求乙液体的折射率。

【答案】(1)5n≥甲；(2)2n >乙【解析】 【详解】(1)盛满甲液体，如图甲所示，P 点刚好全反射时为最小折射率，有1sin n C=由几何关系知222sin 2R C R R =⎛⎫+ ⎪⎝⎭解得5n =则甲液体的折射率应为5n ≥甲(2)盛满乙液体，如图乙所示，与底边平行的光线刚好射入液体时对应液体的最小折射率，A 点1sin n C ='乙 由几何关系得90C α'=︒-B 点恰好全反射有C α'=解各式得2n =乙则乙液体的折射率应为2n >乙2．如图所示，直线Oa 和Ob 的夹角为30︒，在两直线所夹的空间内有垂直纸面向里的匀强磁场，磁场向右的区域无限大，磁感应强度为B 。

在P 点有速度相等的正、负离子沿垂直于Oa 方向射入磁场。

两离子的运动轨迹均与Ob 相切，若不计两离子间的相互作用力，则正、负两种离子的比荷之比为（ ）A ．3B 3C ．1:3D ．3:1 【答案】D 【解析】 【详解】如图所示，由左手定则知磁场中的正离子向左偏转、负离子向右偏转。

洛伦兹力提供向心力，正离子有2v q vB m r=正正负离子有2v q vB m R=负负由几何关系知sin 30sin 30r Rr R ︒︒++= 解以上三式得3:1q q m m =负正负正 故选D 。

3．如图所示，七块完全相同的砖块按照图示的方式叠放起来，每块砖的长度均为L ，为保证砖块不倒下，6号砖块与7号砖块之间的距离S 将不超过（ ）A ．3115L B ．2LC ．52L D ．74L 【答案】A 【解析】试题分析：因两部分对称，则可只研究一边即可；1砖受2和3支持力而处于平衡状态，则可由力的合成求得1对2的压力；而2砖是以4的边缘为支点的杠杆平衡，则由杠杆的平衡条件可得出2露出的长度，同理可求得4露出的长度，则可求得6、7相距的最大距离．1处于平衡，则1对2的压力应为2G；当1放在2的边缘上时距离最大；2处于杠杆平衡状态，设2露出的长度为x ，则2下方的支点距重心在()2Lx -处；由杠杆的平衡条件可知：()22L G G x x -=，解得3Lx =，设4露出的部分为1x ；则4下方的支点距重心在1()2L x -处；4受到的压力为2G G +，则由杠杆的平衡条件可知11()()22L GG x G x -=+，解得12L x =，则6、7之间的最大距离应为()13122()3515L L L x x L L ++=++=，A 正确．4．火车以速率1v 向前行驶，司机突然发现在前方同一轨道上距车s 处有另一辆火车，它正沿相同的方向以较小的速率2v 做匀速运动，于是司机立即使车做匀减速运动，该加速度大小为a ，则要使两车不相撞，加速度a 应满足的关系为（ ）A ．()22122vv a s->B ．212v a s>C ．222v a s>D ．()2122v v a s->【答案】D 【解析】 【详解】ABCD.设经过时间t 两车相遇，则有22112v t s v t at +=-整理得()221220at v v t s +-+=要使两车不相撞，则上述方程无解，即()221480v v as ∆=--<解得()2122v v a s->故D 正确ABC 错误｡ 故选D 。

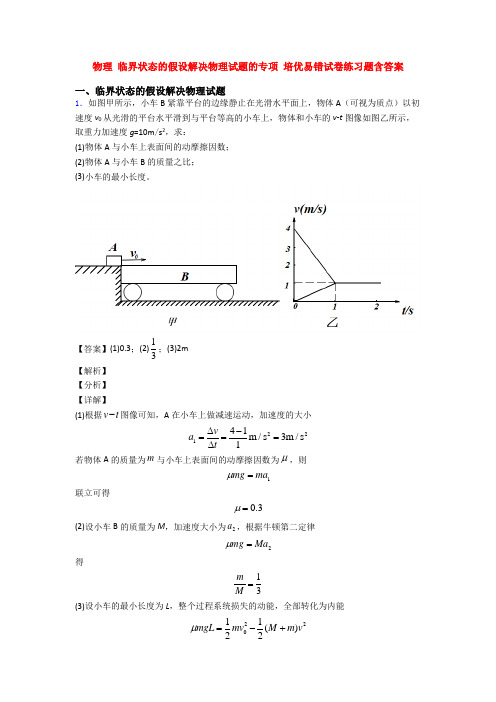
物理 临界状态的假设解决物理试题的专项 培优易错试卷练习题含答案一、临界状态的假设解决物理试题1．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L=2m2．如图所示，C﹑D两水平带电平行金属板间的电压为U，A﹑B为一对竖直放置的带电平行金属板，B板上有一个小孔，小孔在C﹑D两板间的中心线上，一质量为m﹑带电量为＋q的粒子（不计重力）在A板边缘的P点从静止开始运动，恰好从D板下边缘离开，离开时速度度大小为v０，则A﹑B两板间的电压为A．2v2m qUq-B．222mv qUq-C．2mv qUq-D．22mv qUq-【答案】A【解析】【分析】【详解】在AB两板间做直线加速，由动能定理得：2112ABqU mv=；而粒子在CD间做类平抛运动，从中心线进入恰好从D板下边缘离开，根据动能定理：220111222qUmv mv=-；联立两式可得：22ABmv qUUq-=；故选A.【点睛】根据题意分析清楚粒子运动过程是解题的前提与关键，应用动能定理、牛顿第二定律与运动学公式即可解题．3．如图所示，带电粒子（不计重力）以初速度v0从a点垂直于y轴进入匀强磁场，运动过程中经过b点，Oa＝Ob。

备战高考物理临界状态的假设解决物理试题培优练习(含答案)及答案一、临界状态的假设解决物理试题1．一倾角为α的光滑绝缘斜面体固定在水平面上，整个装置处于垂直纸面向里的磁场中，如图所示．一质量为m，电荷量为q的带正电小球从斜面上由静止释放．已知磁感应强度为B，重力加速度为g．求：（1）小球离开斜面时的速率；（2）小球在斜面上滑行的位移大小．【答案】（1）cosmgvqBα=（2）2222cos2sinm gxq Bαα=【解析】(1)小球在斜面上运动,当F N=0时，离开斜面mg cosα=qvBcosmgvqB α=(2)小球在斜面上做匀加速直线运动mg sinα=mav2=2ax解得2222cos2sinm gxq Bαα=2．质量为m的光滑圆柱体A放在质量也为m的光滑“ V”型槽B上，如图，α=60°，另有质量为M的物体C通过跨过定滑轮的不可伸长的细绳与B相连，现将C自由释放，则下列说法正确的是( )A．当M= m时，A和B保持相对静止，共同加速度为0.5gB．当M=2m时，A和B保持相对静止，共同加速度为0.5gC．当M=6m时，A和B保持相对静止，共同加速度为0.75gD．当M=5m时，A和B之间的恰好发生相对滑动【答案】B【解析】 【分析】 【详解】D.当A 和B 之间的恰好发生相对滑动时，对A 受力分析如图根据牛顿运动定律有：cot 60mg ma ︒= 解得cot 603a g g =︒=B 与C 为绳子连接体，具有共同的运动情况，此时对于B 和C 有：()Mg M m a =+所以3M a g g M m ==+，即3MM m=+ 解得3 2.3713M m m =≈-选项D 错误；C.当 2.37M m >，A 和B 将发生相对滑动，选项C 错误；A. 当 2.37M m <，A 和B 保持相对静止。

若A 和B 保持相对静止，则有(2)Mg M m a =+解得2Ma g M m=+所以当M= m 时，A 和B 保持相对静止，共同加速度为13a g =，选项A 错误； B. 当M=2m 时，A 和B 保持相对静止，共同加速度为10.52a g g ==，选项B 正确。

高考物理培优专题复习临界状态的假设解决物理试题练习题及详细答案一、临界状态的假设解决物理试题1．质量为m 2=2Kg 的长木板A 放在水平面上，与水平面之间的动摩擦系数为0.4；物块B （可看作质点）的质量为m 1=1Kg ，放在木板A 的左端，物块B 与木板A 之间的摩擦系数为0.2.现用一水平向右的拉力F 作用在木板A 的右端，让木板A 和物块B 一起向右做匀加速运动．当木板A 和物块B 的速度达到2 m/s 时，撤去拉力，物块B 恰好滑到木板A 的右端而停止滑动，最大静摩擦力等于动摩擦力，g=10m/s 2，求：（1）要使木板A 和物块B 不发生相对滑动，求拉力F 的最大值； （2）撤去拉力后木板A 的滑动时间； （3）木板A 的长度。

【答案】（1）18N （2）0.4s （3）0.6m 【解析】 【详解】（1）当木板A 和物块B 刚要发生相对滑动时，拉力达到最大 以B 为研究对象，由牛顿第二定律得1111m g m a μ=可得2112m/s a g μ==．再以整体为研究对象，由牛顿第二定律得212121 ))F m m g m m a μ-+=+（（ 故得最大拉力18F N =；（2）撤去F 后A 、B 均做匀减速运动，B 的加速度大小仍为1a ，A 的加速度大小为2a ，则 2121122)m m g m g m a μμ+-=（解得225m/s a =故A 滑动的时间220.45v t s s a === （3）撤去F 后A 滑动的距离22122m=0.4m 225v x a ==⨯B 滑动的距离22212m=1m 222v x a ==⨯故木板A 的长度210.6m L x x =-=．【点睛】解题的关键是正确对滑块和木板进行受力分析，清楚滑块和木板的运动情况，根据牛顿第二定律及运动学基本公式求解。

2．如图所示，用长为L =0.8m 的轻质细绳将一质量为1kg 的小球悬挂在距离水平面高为H =2.05m 的O 点，将细绳拉直至水平状态无初速度释放小球，小球摆动至细绳处于竖直位置时细绳恰好断裂，小球落在距离O 点水平距离为2m 的水平面上的B 点，不计空气阻力，取g =10m/s 2求：(1)绳子断裂后小球落到地面所用的时间； (2)小球落地的速度的大小； (3)绳子能承受的最大拉力。

培优临界状态的假设解决物理试题辅导专题训练附答案一、临界状态的假设解决物理试题1．一根细线一端系一小球（可视为质点），另一端固定在光滑圆锥顶上，如图所示，设小球在水平面内做匀速圆周运动的角速度为ω，细线的张力为F T，则F T随ω2变化的图象是（）A．B．C．D．【答案】C【解析】【分析】【详解】由题知小球未离开圆锥表面时细线与竖直方向的夹角为θ，用L表示细线长度，小球离开圆锥表面前，细线的张力为F T，圆锥对小球的支持力为F N，根据牛顿第二定律有F T sinθ－F N cosθ＝mω2L sinθF T cosθ＋F N sinθ＝mg联立解得F T＝mg cosθ＋ω2mL sin2θ小球离开圆锥表面后，设细线与竖直方向的夹角为α，根据牛顿第二定律有F T sinα＝mω2L sinα解得F T＝mLω2故C正确。

故选C。

2．如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m的小球，两绳能承担的最大拉力均为2mg。

当AC和BC均拉直时∠ABC=90°，∠ACB=53°，BC=1m．ABC能绕竖直轴AB匀速转动，因而C球在水平面内做匀速圆周运动．当小球的线速度增大时，两绳均会被拉断，则最先被拉断那根绳及另一根绳被拉断时的速度分别为（已知g=10m/s2，sin53°=0.8，cos53°=0.6）（）A．AC绳 5m/s B．BC绳 5m/sC．AC绳 5.24m/s D．BC绳 5.24m/s【答案】B【解析】【分析】当小球线速度增大时，BC逐渐被拉直，小球线速度增至BC刚被拉直时，对小球进行受力分析，合外力提供向心力，求出A绳的拉力，线速度再增大些，T A不变而T B增大，所以BC绳先断；当BC绳断之后，小球线速度继续增大，小球m作离心运动，AC绳与竖直方向的夹角α增大，对球进行受力分析，根据合外力提供向心力列式求解。

【详解】当小球线速度增大时，BC逐渐被拉直，小球线速度增至BC刚被拉直时，根据牛顿第二定律得：对小球有T A sin∠ACB﹣mg=0 ①T A cos∠ACB+T B=2vml②由①可求得AC绳中的拉力T A=54mg，线速度再增大些，T A不变而T B增大，所以BC绳先断。

【物理】物理临界状态的假设解决物理试题的专项培优练习题(含答案)含详细答案一、临界状态的假设解决物理试题1．如图所示，圆心为O、半径为r的圆形区域外存在匀强磁场，磁场方向垂直于纸面向外，磁感应强度大小为B。

P是圆外一点，OP=3r，一质量为m、电荷量为q（q>0）的粒子从P点在纸面内沿着与OP成60°方向射出（不计重力），求：(1)若粒子运动轨迹经过圆心O，求粒子运动速度的大小；(2)若要求粒子不能进入圆形区域，求粒子运动速度应满足的条件。

【答案】(1)3Bqrm；(2)(332)vm≤+或(332)vm≥-【解析】【分析】【详解】(1)设粒子在磁场中做圆周运动的半径为R，圆心为O'，依图题意作出轨迹图如图所示：由几何知识可得：OO R'=()222(3)6sinOO R r rRθ'=+-解得3R r=根据牛顿第二定律可得2vBqv mR=解得3Bqrvm=(2)若速度较小，如图甲所示：根据余弦定理可得()22211196sin r R R r rR θ+=+-解得1332R =+若速度较大，如图乙所示：根据余弦定理可得()22222296sin R r R r rR θ-=+-解得2332R =-根据BqRv m=得1(332)v m =+，2(332)v m =-若要求粒子不能进入圆形区域，粒子运动速度应满足的条件是(332)v m ≤+或(332)v m≥-2．中国已进入动车时代，在某轨道拐弯处，动车向右拐弯，左侧的路面比右侧的路面高一些，如图所示，动车的运动可看作是做半径为R 的圆周运动，设内外路面高度差为h ，路基的水平宽度为d ，路面的宽度为L ，已知重力加速度为g ，要使动车轮缘与内、外侧轨道无挤压，则动车拐弯时的速度应为（ ）A．gRhLB．gRhdC．2gRD．gRdh【答案】B【解析】【详解】把路基看做斜面，设其倾角为θ，如图所示当动车轮缘与内、外侧轨道无挤压时，动车在斜面上受到自身重力mg和斜面支持力N，二者的合力提供向心力，即指向水平方向，根据几何关系可得合力F=mg tanθ，合力提供向心力，根据牛顿第二定律，有mg tanθ＝2 v mR计算得v tangRθtanθ＝h d带入解得v gRhdgRhd压，故B正确，ACD错误。

【物理】培优临界状态的假设解决物理试题辅导专题训练附答案一、临界状态的假设解决物理试题1．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L =2m2．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

圆形底面的直径为2R ，圆筒的高度为R 。

(1)若容器内盛满甲液体，在容器中心放置一个点光源，在侧壁以外所有位置均能看到该点光源，求甲液体的折射率；(2)若容器内装满乙液体，在容器下底面以外有若干个光源，却不能通过侧壁在筒外看到所有的光源，求乙液体的折射率。

【答案】(1)5n≥甲；(2)2n >乙【解析】 【详解】(1)盛满甲液体，如图甲所示，P 点刚好全反射时为最小折射率，有1sin n C=由几何关系知222sin 2R C R R =⎛⎫+ ⎪⎝⎭解得5n =则甲液体的折射率应为5n ≥甲(2)盛满乙液体，如图乙所示，与底边平行的光线刚好射入液体时对应液体的最小折射率，A 点1sin n C ='乙 由几何关系得90C α'=︒-B 点恰好全反射有C α'=解各式得2n =乙则乙液体的折射率应为2n >乙3．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。

培优 易错 难题临界状态的假设解决物理试题辅导专题训练附详细答案一、临界状态的假设解决物理试题1．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L =2m2．水平传送带上A 、B 两端点间距L ＝4m ，半径R ＝1m 的光滑半圆形轨道固于竖直平面内，下端与传送带B 相切。

传送带以v 0＝4m/s 的速度沿图示方向匀速运动，m ＝lkg 的小滑块由静止放到传送带的A 端，经一段时间运动到B 端，滑块与传送带间的动摩擦因数μ＝0.5，g ＝10m/s 2。

(1)求滑块到达B 端的速度；(2)求滑块由A 运动到B 的过程中，滑块与传送带间摩擦产生的热量；(3)仅改变传送带的速度，其他条件不变，计算说明滑块能否通过圆轨道最高点C 。

【答案】(1)v B =4m/s ； (2)Q ＝8J ； (3)不能通过最高点 【解析】 【分析】本题考查了动能定理和圆周运动。

【详解】⑴滑块在传送带上先向右做加速运动，设当速度v = v 0时已运动的距离为x 根据动能定理201-02mgx mv μ=得x=1.6m ＜L所以滑块到达B 端时的速度为4m/s 。

物理临界状态的假设解决物理试题的专项培优练习题(含答案)附答案一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ= 【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．一根细线一端系一小球（可视为质点），另一端固定在光滑圆锥顶上，如图所示，设小球在水平面内做匀速圆周运动的角速度为ω，细线的张力为F T ，则F T 随ω2变化的图象是（ ）A．B．C．D．【答案】C【解析】【分析】【详解】由题知小球未离开圆锥表面时细线与竖直方向的夹角为θ，用L表示细线长度，小球离开圆锥表面前，细线的张力为F T，圆锥对小球的支持力为F N，根据牛顿第二定律有F T sinθ－F N cosθ＝mω2L sinθF T cosθ＋F N sinθ＝mg联立解得F T＝mg cosθ＋ω2mL sin2θ小球离开圆锥表面后，设细线与竖直方向的夹角为α，根据牛顿第二定律有F T sinα＝mω2L sinα解得F T＝mLω2故C正确。

故选C。

3．中国已进入动车时代，在某轨道拐弯处，动车向右拐弯，左侧的路面比右侧的路面高一些，如图所示，动车的运动可看作是做半径为R的圆周运动，设内外路面高度差为h，路基的水平宽度为d，路面的宽度为L，已知重力加速度为g，要使动车轮缘与内、外侧轨道无挤压，则动车拐弯时的速度应为（）A gRhLBgRhdC2gRDgRdh【答案】B【解析】 【详解】把路基看做斜面，设其倾角为θ，如图所示当动车轮缘与内、外侧轨道无挤压时，动车在斜面上受到自身重力mg 和斜面支持力N ，二者的合力提供向心力，即指向水平方向，根据几何关系可得合力F =mg tan θ，合力提供向心力，根据牛顿第二定律，有mg tan θ＝2v m R计算得v ＝tan gR θ，根据路基的高和水平宽度得tan θ＝h d带入解得v ＝gRh d ，即动车拐弯时的速度为gRhd时，动车轮缘与内、外侧轨道无挤压，故B 正确，ACD 错误。